Явная схема для решения уравнения теплопроводности

Видео:Решение задачи теплопроводности (Явная разностная схема)Скачать

Уравнение теплопроводности

Ранее (см. разд. 2.1.2, 2.1.3) уже были построены и исследованы разностные схемы решения смешанной задачи для одномерного уравнения теплопроводности:

(2.75)

Были получены две двухслойные схемы — явная (2.3) и неявная (2.4). В явной схеме значения сеточной функции на верхнем (j + 1)-ом слое вычисляли с помощью решения на нижнем слое [соотношение (2.13)]. Для нахождения решения на (j + 1)-м слое по неявной схеме была получена трехдиагональная система линейных алгебраических уравнений (2.22), которую решают методом прогонки.

Неявная схема безусловно устойчива, явная схема устойчива при выполнении условия

Обе схемы сходятся к решению исходной задачи со скоростью .

Схемы (2.3), (2.4) построены для случая, когда значения искомой функции (температуры) Uна границах х = 0, х = 1определяются заданными функциями . Однако граничные условия в смешанной задаче (2.75) могут быть и иными, в них может входить производная искомой функции. Например, если конец стержня х=0 теплоизолирован, то условие имеет вид

В этом случае, как и при решении волнового уравнения, данное условие нужно записывать в схемах (2.3), (2.4) в разностном виде.

Перейдем теперь к построению разностных схем для уравнения теплопроводности с двумя пространственными переменными. Примем для простоты а = 1. Тогда это уравнение можно записать в виде

(2.76)

Пусть при t=0 начальное условие задано в виде

(2.77)

В отличие от волнового уравнения, требующего два начальных условия, в уравнение теплопроводности входит только первая производная по t, и необходимо задавать одно начальное условие.

Часто задачи теплопроводности или диффузии, описываемые двумерным уравнением (2.76), решаются в ограниченной области. Тогда, кроме начального условия (2.77), нужно формулировать граничные условия. В частности, если расчетная область представляет прямоугольный параллелепипед (рис. 2.24), то нужно задавать граничные условия на его боковых гранях. Начальное условие (2.77) задано на нижнем основании параллелепипеда.

Рис. 2.24. Расчетная область

Введем простейшую сетку с ячейками в виде прямоугольных параллелепипедов, для чего проведем три семейства плоскостей: хi= ih1(i=0,1. I), (j=0,1. J), . Значение сеточной функции в узлах обозначим символом . С помощью этих значений можно построить разностные схемы для уравнения (2.76).

Рассмотренные выше схемы для одномерного уравнения легко обобщаются на двумерный случай.

Построим явную разностную схему, шаблон которой изображен на рис. 2.25. Аппроксимируя производные отношениями конечных разностей, получаем следующее сеточное уравнение:

Рис. 2.25. Шаблон двумерной схемы

Отсюда можно найти явное выражение для значения сеточной функции на (k + 1)-ом слое:

(2.78)

Условие устойчивости имеет вид

(2.79)

При получается особенно простой вид схемы (2.78):

(2.80)

Полученная схема сходится со скоростью

Формулы (2.78) или (2.80) представляют собой рекуррентные соотношения для последовательного вычисления сеточной функции во внутренних узлах слоев k = 1,2. К. На нулевом слое используется начальное условие (2.77), которое записывается в виде

(2.81)

Значения в граничных узлах вычисляют с помощью граничных условий.

Алгоритм решения смешанной задачи для двумерного уравнения теплопроводности изображен на рис. 2.26. Здесь решение хранится на двух слоях: нижнем (массив ) и верхнем (массив ). Блоки граничных условий необходимо сформировать в зависимости от конкретного вида этих условий. Результаты выводят на каждом слое, хотя можно ввести шаг выдачи (см. рис. 2.13).

Рис. 2.26. Алгоритм решения двумерного уравнения теплопроводности

Построим теперь абсолютно устойчивую неявную схему для решения уравнения (2.76), аналогичную схеме (2.4) для одномерного уравнения теплопроводности. Аппроксимируя в (2.76) вторые производные по пространственным переменным на (k + 1)-ом слое, получаем следующее разностное уравнение:

(2.82)

Это уравнение можно записать в виде системы линейных алгебраических уравнений относительно значений сеточной функции на каждом слое:

(2.83)

К этой системе уравнений нужно добавить граничные условия для определения значений сеточной функции в граничных узлах (т.е. при i= 0, I; j = 0, J). На нулевом слое решение находится из начального условия (2.77), представленного в виде (2.81).

Система (2.83), полученная для двумерного уравнения теплопроводности, имеет более сложный вид, чем аналогичная система (2.22) для одномерного случая, которую можно решить методом прогонки. Таким образом, распространение неявной схемы на многомерный случай приводит к значительному усложнению вычислительного алгоритма и увеличению объема вычислений.

Недостатком явной схемы (2.78) является жесткое ограничение на шаг по времени τ, вытекающее из условия (2.79). Существуют абсолютно устойчивые экономичные разностные схемы, позволяющие вести расчет со сравнительно большим значением шага по времени и требующие меньшего объема вычислений. Две из них будут рассмотрены в разд. 2.3.3.

Видео:Решение уравнения теплопроводности в одномерной постановке в Excel с применением неявной схемыСкачать

Устойчивые явные схемы для уравнения теплопроводности Текст научной статьи по специальности « Математика»

Видео:Лекция №1.1 Явная и неявная схемы для уравнения теплопроводностиСкачать

Аннотация научной статьи по математике, автор научной работы — Геренштейн А. В., Геренштейн Е. А., Машрабов Н.

Предлагается численный метод интегрирования уравнения теплопроводности , основанный на комбинации явной и неявной схемы с использованием линейных дифференциальных уравнений первого порядка (обыкновенных или с частными производными в зависимости от наличия исходном уравнении производных первого порядка по пространственным переменным).

Видео:Решение уравнения теплопроводности в одномерной постановке в ExcelСкачать

Похожие темы научных работ по математике , автор научной работы — Геренштейн А. В., Геренштейн Е. А., Машрабов Н.

Видео:Решение уравнения теплопроводности методом конечных разностейСкачать

Steady Obvious Schemes for Equation of Heat Conductivity

In given clause the numerical method of integration for equation of heat conductivity , based on a combination of the obvious and implicit scheme with use of the linear differential first-order equation (ordinary or partial differential depending on presence in the initial equation of first-order derivatives on spatial variables) is offered.

Видео:01 Теплопроводность, явныйСкачать

Текст научной работы на тему «Устойчивые явные схемы для уравнения теплопроводности»

УСТОЙЧИВЫЕ ЯВНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ

A.B. Геренштейн, Е.А. Геренштейн, Н. Машрабов

Предлагается численный метод интегрирования уравнения теплопроводности, основанный на комбинации явной и неявной схемы с использованием линейных дифференциальных уравнений первого порядка (обыкновенных или с частными производными — в зависимости от наличия в исходном уравнении производных первого порядка по пространственным переменным).

Ключевые слова: уравнение теплопроводности, устойчивый, явная схема, дифференциальное уравнение первого порядка.

Рассмотрим одномерное уравнение теплопроводности

ди _ д2и дЬ дх2′

Обозначим через г шаг по переменной через Н — шаг по переменной х. Через иг-, щ, щ+ обозначим значения функции и при і = ¿о (на оси х) в точках жг_і, Хі, Хі+і, через Щ-і, Щ, щ+ обозначим значения функции и при і = ¿о + т в тех же точках (см. рисунок). Зная значения щ (г = 1, 2, . п) нам надо вычислить значения щ (г = 1, 2, . п).

Коэффициенты уравнения (1) и обозначения приведены к безразмерному виду.

Явная схема выглядит так [1, 2]:

і, иг, щ+ уже вычислены). Неявная схема выглядит так [1, 2]:

Это приводит к решению системы линейных алгебраических уравнений с так называемой трехдиагональной матрицей. Для одномерного уравнения эта схема предпочтительна, ибо явная схема неустойчива при г > Н2/2, в то время как неявная схема устойчива при всех значениях т.

Однако в многомерных случаях неявная схема оказывается не столь удобной. Имея в виду дальнейшие применения численных методов к многомерному уравнению, запишем такую схему

Устойчивые явные схемы для уравнения теплопроводности

и перейдем к пределу при т -* 0. Получим обыкновенное дифференциальное уравнение

d&i 2 _ Щ—і + ttj-j-x /г

где д = ехр(—2т/к2) 1, то схема неустойчива.

Теперь рассмотрим уравнение теплопроводности для двумерного случая в полярной системе координат

ди _ 1 д ( ди 1 д2и . .

Обозначим к — шаг по переменной г, т — шаг по переменной ¿, а — шаг по переменной ір. Явная схема выглядит так

2?”з + к 2гі к т / щгк—1 -|- щ,к— 2и^ т

Щк — иш + ^ Щ+1,к + 2Гі иг-1,к 2Щк j ^ r2 r2 J а2’ (8)

Здесь г — номер узла сетки по г, к — номер узла сетки по

Щ,, ^иле. “J + (I -с >‘г) (12)

т.е. опять возникает устойчивая явная схема.

Однако во многих случаях приходится рассматривать вращающуюся систему координат с постоянной угловой скоростью OJ [3].

Тогда уравнение примет вид

ди ди _ 1 д ( ди 1 д2и . .

dt Ш дір г дг дг) г2 дір2

Вестник ЮУрГУ, №15(115), 2008

A.B. Геренштейн, E.A. Геренштейн, H. Машрабов

В этом случае для устойчивости схемы приходим к линейному уравнению в частных производных первого порядка

д _ д _ _ . . uik w «Ь ßuik — Jik• (14)

Здесь предполагается, что для каждого значения г правая часть является функцией (разумеется, известной) аргумента + шт) означают узлы (г, к) сетки, при которых щк = u^ip + шт), т.е. значение (р + шт попадает в узел (*, к).

Аналогичный смысл имеет выражение f(

Таким образом, выражение (15) задает явную устойчивую схему для уравнения теплопроводности во вращающейся с угловой скоростью ш полярной системе координат; интеграл в правой части (15) предполагает численное интегрирование заданных в узлах сетки функции.

Видео:Решение нестационарного уравнения теплопроводности в двухмерной постановке в ExcelСкачать

Уравнение теплопроводности в tensorflow

Привет, Хабр! Некоторое время назад увлекся глубоким обучением и стал потихоньку изучать tensorflow. Пока копался в tensorflow вспомнил про свою курсовую по параллельному программированию, которую делал в том году на 4 курсе университета. Задание там формулировалось так:

Линейная начально-краевая задача для двумерного уравнения теплопроводности:

Хотя правильнее было бы назвать это уравнением диффузии.

Задачу тогда требовалось решить методом конечных разностей по неявной схеме, используя MPI для распараллеливания и метод сопряженных градиентов.

Я не специалист в численных методах, пока не специалист в tensorflow, но опыт у меня уже появился. И я загорелся желанием попробовать вычислять урматы на фреймворке для глубокого обучения. Метод сопряженных градиентов реализовывать второй раз уже не интересно, зато интересно посмотреть как с вычислением справится tensorflow и какие сложности при этом возникнут. Этот пост про то, что из этого вышло.

Видео:Метод Фурье для неоднородного уравнения теплопроводностиСкачать

Численный алгоритм

Разностная схема:

Чтобы проще было расписывать, введем операторы:

Явная разностная схема:

В случае явной разностной схемы для вычисления используются значения функции в предыдущий момент времени и не требуется решать уравнение на значения . Однако такая схема менее точная и требует значительно меньший шаг по времени.

Неявная разностная схема:

Перенесем в левую сторону все связанное с , а в правую и домножим на :

По сути мы получили операторное уравнение над сеткой:

что, если записать значения в узлах сетки как обычный вектор, является обычной системой линейных уравнений (). Значения в предыдущий момент времени константы, так как уже рассчитаны.
Для удобства представим оператор как разность двух операторов:

Заменив на нашу оценку , запишем функционал ошибки:

где — ошибка в узлах сетки.

Будем итерационно минимизировать функционал ошибки, используя градиент.

В итоге задача свелась к перемножению тензоров и градиентному спуску, а это именно то, для чего tensorflow и был задуман.

Видео:Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Реализация на tensorflow

Кратко о tensorflow

В tensorflow сначала строится граф вычислений. Ресурсы под граф выделяются внутри tf.Session. Узлы графа — это операции над данными. Ячейками для входных данных в граф служат tf.placeholder. Чтобы выполнить граф, надо у объекта сессии запустить метод run, передав в него интересующую операцию и входные данные для плейсхолдеров. Метод run вернет результат выполнения операции, а также может изменить значения внутри tf.Variable в рамках сессии.

tensorflow сам умеет строить графы операций, реализующие backpropagation градиента, при условии, что в оригинальном графе присутствуют только операции, для которых реализован градиент (пока не у всех).

Сначала код инициализации. Здесь производим все предварительные операции и считаем все, что можно посчитать заранее.

По-хорошему надо было считать значения функции на краях заданными и оптимизировать значения функции только во внутренней области, но с этим возникли проблемы. Способа сделать оптимизируемым только часть тензора не нашлось, и у операции присвоения значения срезу тензора не написан градиент (на момент написания поста). Можно было бы попробовать хитро повозиться на краях или написать свой оптимизатор. Но и просто добавление разности на краях значений функции и краевых условий в функционал ошибки хорошо работает.

Стоит отметить, что метод с адаптивным моментом показал себя наилучшим образом, пусть функционал ошибки и квадратичный.

Вычисление функции: в каждый момент времени делаем несколько оптимизационных итераций, пока не превысим maxiter или ошибка не станет меньше eps, сохраняем и переходим к следующему моменту.

Запуск:

Видео:Основы теплотехники. Лекция 1. Основные понятия и определения (предварительная версия)Скачать

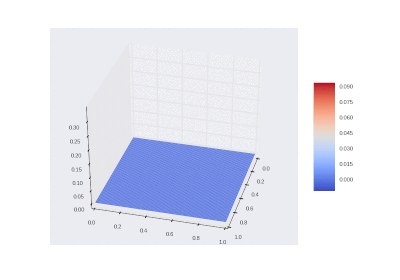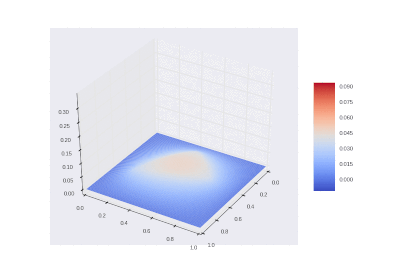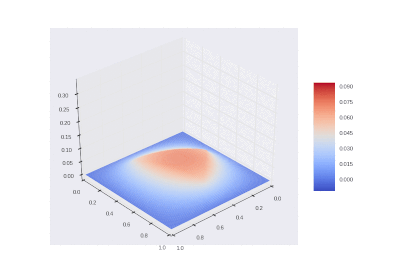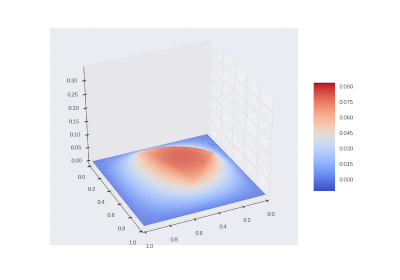
Результаты

Условие как и оригинальное, но без в уравнении:

Что легко правится в коде:

Разницы почти нет, потому что производные имеют большие порядки, чем сама функция.

Условие с одним нагревающимся краем:

Условие с остыванием изначально нагретой области:

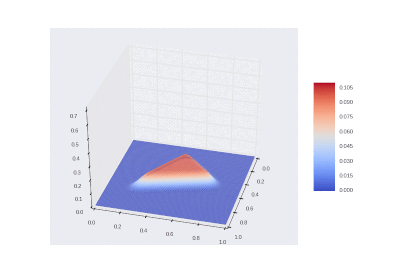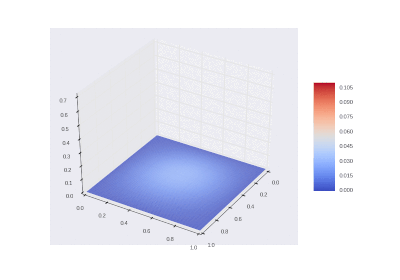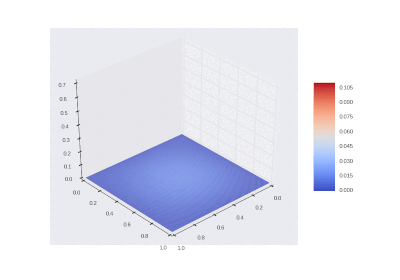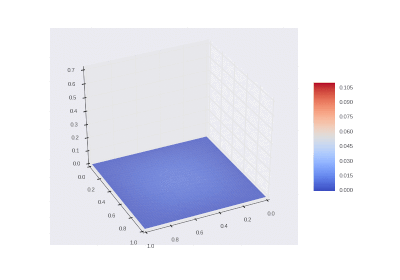
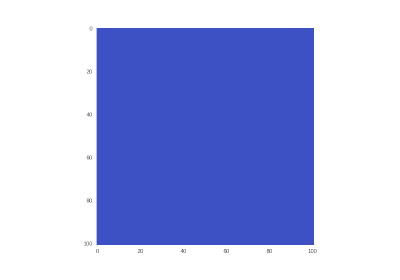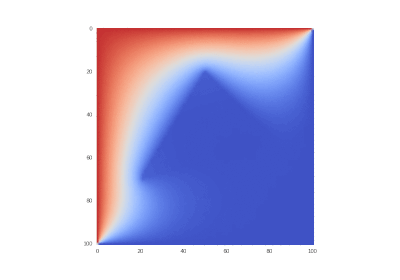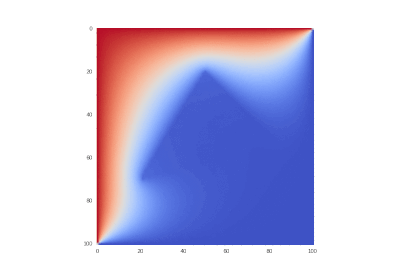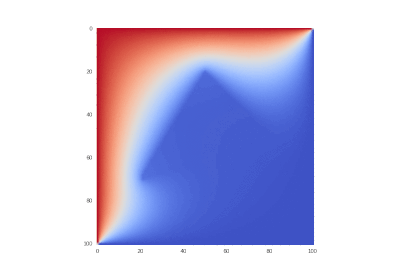
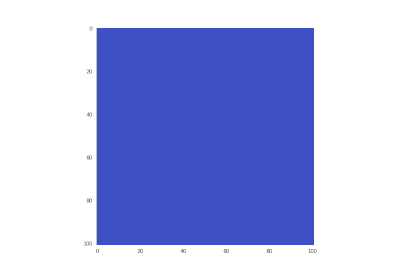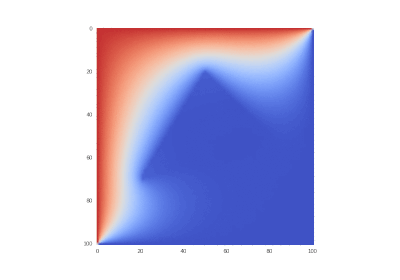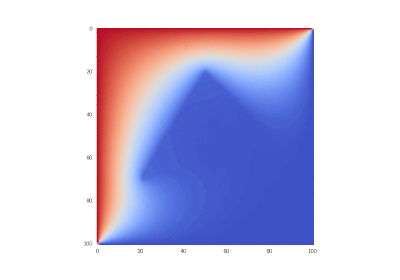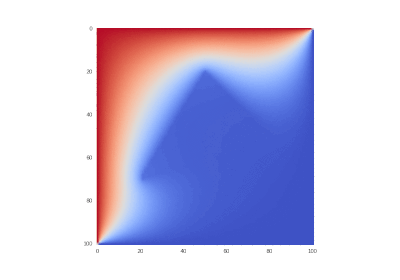
Условие с включением нагрева в области:

Видео:Уравнение в частных производных Уравнение теплопроводностиСкачать

Рисование гифок

Функция рисования 3D-гифки:

В основной класс добавляем метод, возвращающий U в виде pandas.DataFrame

Функция рисования 2D-гифки:

Стоит отметить, что оригинальное условие без использования GPU считалось 4м 26с, а с использованием GPU 2м 11с. При больших значениях точек разрыв растет. Однако не все операции в полученном графе GPU-совместимы.

• Intel Core i7 6700HQ 2600 МГц,
• NVIDIA GeForce GTX 960M.

Посмотреть, какие операции на чем выполняются, можно с помощью следующего кода:

Это был интересный опыт. Tensorflow неплохо показал себя для этой задачи. Может быть даже такой подход получит какое-то применение — всяко приятнее писать код на питоне, чем на C/C++, а с развитием tensorflow станет еще проще.

🎬 Видео

Численные методы математической физики - Решение смешанной задачи для уравнения теплопроводностиСкачать

Решение задачи Коши для уравнения теплопроводности (Часть 1)Скачать

Шокирующая правда: почему ученица не поступила из-за сбоя госуслуг | ЕГЭLANDСкачать

Принцип максимума для уравнения теплопроводности на отрезкеСкачать

Уравнение теплопроводности на полупрямой (решение задачи)Скачать

8.1 Решение уравнения теплопроводности на отрезкеСкачать

Математика в неожиданных местах: Разностная схема для уравнения теплопроводностиСкачать

Решение первой краевой задачи для неоднородного уравнения теплопроводности.Скачать

Решение неоднородного уравнения теплопроводностиСкачать