Одним из наиболее распространенных в инженерной практике уравнений с частными производными второго порядка является волновое уравнение, описывающее различные виды колебаний. Поскольку колебания — процесс нестационарный, то одной из независимых переменных является время t. Кроме того, независимыми переменными в уравнении являются также пространственные координаты х, у, z. В зависимости от их количества различают одномерное, двумерное и трехмерное волновые уравнения.
Одномерное волновое уравнение – уравнение, описывающее продольные колебания стержня, сечения которого совершают плоскопараллельные колебательные движения, а также поперечные колебания тонкого стержня (струны) и другие задачи. Двумерное волновое уравнение используют для исследования колебаний тонкой пластины (мембраны). Трехмерное волновое уравнениеописывает распространение волн в пространстве (например, звуковых волн в жидкости, упругих волн в сплошной среде и т.п.).
Рассмотрим одномерное волновое уравнение, которое можно записать в виде

Для поперечных колебаний струны искомая функция U(x,t) описывает положение струны в момент t. В этом случае а2 = Т/ρ, где Т — натяжение струны, ρ — ее линейная (погонная) плотность. Колебания предполагаются малыми, т.е. амплитуда мала по сравнению с длиной струны. Кроме того, уравнение (2.63) записано для случая свободных колебаний. В случае вынужденных колебаний в правой части уравнения добавляют некоторую функцию f(x,t), характеризующую внешние воздействия, при этом сопротивление среды колебательному процессу не учитывается.
Простейшей задачей для уравнения (2.63) является задача Коши: в начальный момент времени задаются два условия (количество условий равно порядку входящей в уравнение производной по t):

Эти условия описывают начальную форму струны 

На практике чаще приходится решать не задачу Коши для бесконечной струны, а смешанную задачу для ограниченной струны некоторой длины l. В этом случае задают граничные условия на ее концах. В частности, при закрепленных концах их смещения равны нулю, и граничные условия имеют вид

Рассмотрим некоторые разностные схемы для решения задачи (2.63)-(2.65). Простейшей является явная трехслойная схема типа крест (шаблон показан на рис. 2.21). Заменим в уравнении (2.63) вторые производные искомой функции Uпо tи х их конечно-разностными соотношениями с помощью значений сеточной функции 

Рис. 2.21. Шаблон явной схемы
Отсюда можно найти явное выражение для значения сеточной функции на ( j + 1)-ом слое:

Здесь, как обычно в трехслойных схемах, для определения неизвестных значений на (j + 1)-ом слое нужно знать решения на j-ом и (j — 1)-ом слоях. Поэтому начать счет по формулам (2.66) можно лишь для второго слоя, а решения на нулевом и первом слоях должны быть известны. Их находят с помощью начальных условий (2.64). На нулевом слое имеем

Для получения решения на первом слое воспользуемся вторым начальным условием (2.64). Производную 

Из этого соотношения можно найти значения сеточной функции на первом временном слое:

Отметим, что аппроксимация начального условия в виде (2.68) ухудшает аппроксимацию исходной дифференциальной задачи: погрешность аппроксимации становится порядка 

Вместо 

Тогда (2.70) примет вид:

Разностная схема (2.66) с учетом (2.71) обладает погрешностью аппроксимации порядка
При решении смешанной задачи с граничными условиями вида (2.65), т.е. когда на концах рассматриваемого отрезка заданы значения самой функции, второй порядок аппроксимации сохраняется. В этом случае для удобства крайние узлы сетки располагают в граничных точках (х0=0, xI = l). Однако граничные условия могут задаваться и для производной.
Например, в случае свободных продольных колебаний стержня на его незакрепленном конце задается условие

Если это условие записать в разностном виде с первым порядком аппроксимации, то погрешность аппроксимации схемы станет порядка 
Рассмотренная разностная схема (2.66) решения задачи (2.63) — (2.65) условно устойчива. Необходимое и достаточное условие устойчивости:

Следовательно, при выполнении этого условия и с учетом аппроксимации схема (2.66) сходится к исходной задаче со скоростью O(h2+τ2). Данная схема часто используется в практи-ческих расчетах. Она обеспечивает приемлемую точность получения решения U(x,t), которое имеет непрерывные производные четвертого порядка.
Рис. 2.22. Алгоритм решения волнового уравнения
Алгоритм решения задачи (2.63)-(2.65) с помощью данной явной разностной схемы приведен на рис. 2.22. Здесь представлен простейший вариант, когда все значения сеточной функции, образующие двумерный массив, по мере вычисления хранятся в памяти компьютера, а после решения задачи выводятся результаты. Можно было бы предусмотреть хранение решения лишь на трех слоях, что сэкономило бы память. Результаты в таком случае можно выводить в процессе счета (см. рис. 2.13).
Существуют и другие разностные схемы решения волнового уравнения. В частности, иногда удобнее использовать неявные схемы, чтобы избавиться от ограничений на величину шага, налагаемых условием (2.73). Эти схемы обычно абсолютно устойчивы, однако алгоритм решения задачи и программа для компьютера усложняются.
Построим простейшую неявную схему. Вторую производную по tв уравнении (2.63) аппроксимируем, как и ранее, по трехточечному шаблону с помощью значений сеточной функции на слоях j— 1, j, j + 1. Производную до х заменяем полусуммой ее аппроксимации на (j + 1)-ом и (j— 1)-ом слоях (рис. 2.23):
Рис. 2.23. Шаблон неявной схемы
Из этого соотношения можно получить систему уравнений относительно неизвестных значений сеточной функции на (j+ 1)-ом слое:

Полученная неявная схема устойчива и сходится со скоростью 
При двух или трех независимых пространственных переменных волновые уравнения принимают вид
Для них также могут быть построены разностные схемы по аналогии с одномерным волновым уравнением. Разница состоит в том, что нужно аппроксимировать производные по двум или трем пространственным переменным, что, естественно, усложняет алгоритм и требует значительно больших объемов памяти и времени счета. Подробнее двумерные задачи будут рассмотрены ниже для уравнения теплопроводности.
Видео:Задача Коши для волнового уравнения (Часть 1)Скачать

Разностные схемы для уравнения гиперболического типа.
Читайте также:
|










 , (1) 0 2 ) соответственно.
, (1) 0 2 ) соответственно. — множитель перехода для схемы с центральной разностью.
— множитель перехода для схемы с центральной разностью.
 – число Куранта
– число Куранта может не стремится к нулю при
может не стремится к нулю при  . Однако если число Куранта
. Однако если число Куранта  , то при
, то при  условие согласованности выполняется.
условие согласованности выполняется.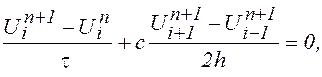




 . Метод устойчив при
. Метод устойчив при 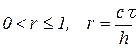

 не зависит от
не зависит от  , что приводит к появлению двух независимых решений;
, что приводит к появлению двух независимых решений;


 и
и  на центральные разности 2-го порядка, получим:
на центральные разности 2-го порядка, получим:
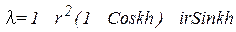



 на
на 


 Подставляя вместо членов с производной по x —
Подставляя вместо членов с производной по x —  замену центральной разностью, получаем
замену центральной разностью, получаем





 (8.11)
(8.11) (8.12)
(8.12) (8.13)
(8.13)
 .
. ,
,  .
. зададим точки:
зададим точки: (8.14)
(8.14) ,
,  ,
,  , и заменим производные разностными формулами
, и заменим производные разностными формулами , (8.15)
, (8.15) приближенные значения искомой функции в точках
приближенные значения искомой функции в точках  (8.16)
(8.16)
 . (8.17)
. (8.17) . (8.18)
. (8.18) . (8.19)
. (8.19) в (8.12), из (8.18), (8.19) выводим формулу для вычисления значений функции на первом слое:
в (8.12), из (8.18), (8.19) выводим формулу для вычисления значений функции на первом слое: . (8.20)
. (8.20) . (8.21)
. (8.21) :
: (8.22)
(8.22) (8.29)
(8.29) (8.30)
(8.30) (8.31)
(8.31) (8.32)
(8.32) (8.33)
(8.33) (8.34)
(8.34)















