- Владислав Грузинский 5 лет назад Просмотров:
1 Разностная аппроксимация начально-краевой задачи для уравнения теплопроводности. Понятие явной и неявной схемы. 1 Разностная аппроксимация уравнения теплопроводности Рассмотрим различные варианты разностной аппроксимации линейного одномерного по пространству уравнения теплопроводности: где T > 0 некоторая константа. u t = u + fx, t, x 0, l, t 0, T ], 1.1 x Введем в области D = равномерную сетку с шагом по координате и шагом по времени: x =, = 0, 1. = l; t j = j, j = 0, 1. M, M = T. Уравнение 1.1 содержит как производные по пространственной переменной x, так и по времени t, поэтому для построения его разностной аппроксимации придется использовать узлы сетки, соответствующие различным j. Все узлы сетки, отвечающие фиксированному j, называют j-м временным слоем. Свойства разностных схем для уравнения 1.1 зависят от того, на каком слое j по времени аппроксимируется выражение u x. Рассмотрим возможные варианты. Вариант 1: явная схема. Для аппроксимации оператора L = t x приведенный на рис. 1. в уравнении 1.1 используем шаблон, 1
2 Рис. 1: Шаблон явной схемы для уравнения теплопроводности. Соответствующий разностный оператор L 0 u имеет вид: L 0 ux, t + ux, t ux +, t ux, t + ux, t u =. Далее для краткости будем использовать следующие стандартные обозначения: u = ux, t; û = ux, t +. Тогда: u t = û u, L 0 u = u t u xx. Найдем погрешность аппроксимации разностным оператором L 0 исходного дифференциального оператора L в точке x, t. В случае достаточно гладкой функции ux, t при достаточно малых шагах и имеем: u t = ux, t + ux, t = ux, t t + O, 1. Следовательно, разностный оператор L 0 аппроксимирует дифференциальный оператор L с погрешностью O + в точке x, t: L 0 u xx = ux, t x + O. 1.3 ux, t u = t ux, t x > <L[ux,t] +O +. Введем сеточную функцию ϕ = ϕx, t j, аппроксимирующую правую часть fx, t уравнения 1.1 на всех внутренних узлах x, t j сетки с погрешностью O +. В качестве ϕ можно взять, например ϕx, t j = fx, t j. Тогда разностное уравнение L 0 y = ϕ будет аппроксимировать исходное дифференциальное уравнение теплопроводности 1.1 с первым порядком погрешности по и вторым по.
3 Вариант. Чисто неявная схема. Используем для аппроксимации оператора L = t x приведенный на рис.. в уравнении 1.1 шаблон, Рис. : Шаблон неявной схемы для уравнения теплопроводности. Тогда разностная аппроксимация оператора L уравнения теплопроводности будет выглядеть следующим образом: L 1 ux, t + ux, t ux +, t + ux, t + + ux, t + u = = u t û xx. Рассмотрим погрешность аппроксимации разностным оператором L 1 исходного дифференциального оператора L в точках x, t, x, t +. Так как для достаточно гладкой функции ux, t справедливы равенства û xx = ux, t + x + O = ux, t x + O +, 1.4 то с учетом 1. получаем, что оператор L 1 аппроксимирует дифференциальный оператор L в уравнении 1.1 с погрешностью O + в точках x, t и x, t + : L 1 ux, t u = t ux, t x > <L[ux,t] +O + ux, t + = ux, t + +O +. > t <L[ux,t+] Беря в качестве сеточной аппроксимации правой части уравнения 1.1, например, функцию ϕx, t j = fx, t j+1, получим разностное уравнение L 1 y = ϕ, аппроксимирующее 1.1 с погрешностью O +. 3
4 Вариант 3. Неявная схема с весами. Используем шаблон, приведенный на рис. 3, и линейную комбинацию операторов L 0 и L 1 для аппроксимации дифференциального оператора L: L σ u = σl1 u+1 σl0 u = σu t σû xx +1 σu t 1 σu xx = u t σû xx + 1 σu xx, где σ 0, 1. Рис. 3: Шаблон неявной схемы с весами для уравнения теплопроводности. Пользуясь равенствами 1., 1.3 и 1.4, получаем, что оператор L σ аппроксимирует исходный дифференциальный оператор L с погрешностью O + в точках x, t, x, t+ при любом σ. По определению погрешность ψx, t = L σ u Lu 1.5 аппроксимации выражения Lu разностным выражением L σ u может вычисляться в любой точке x, t, а не обязательно в каком-либо узле сетки, так как в соотношении 1.5 функция ux, t это произвольная достаточно гладкая функция непрерывных аргументов x и t. Поэтому рассмотрим погрешность аппроксимации оператором L σ дифференциального оператора L в центральной точке x, t шаблона, приведенного на рис. 3. Пользуясь для достаточно гладкой функции ux, t разложением в ряд Тейлора в окрестности точки x, t + 0.5, при малых и получаем: ux, t + ux, t u t = = u t + O, x,t+0.5 û xx = u x + O = u x,t+ x + 3 u x,t+0.5 t x + O +, x,t+0.5 u xx = u x + O = u x,t x x,t u t x + O +. x,t+0.5 4
5 Следовательно, при σ = 0.5 в точке x, t оператор L 0.5 в силу своей симметрии аппроксимирует L со вторым порядком погрешности аппроксимации по и : L σ u = ux, t + t ux, t + x > <L[ux,t+ ] 3 ux, t + σ 1 + O +. > <x t 0 при σ=0.5 Для того, чтобы получить разностное уравнение, аппроксимирующее дифференциальное уравнение u t = u + fx, t x с погрешностью O + в точке x, t +, достаточно взять в качестве сеточной аппроксимации правой части fx, t этого уравнения функцию ϕx, t j = fx, t j Итак, разностное уравнение L 0.5 y = ϕ, где ϕx, t j = fx, t j + 0.5, аппроксимирует уравнение 1.1 со вторым порядком погрешности по и. Реализация явной, неявной и симметричной разностных схем для начально-краевой задачи для уравнения теплопроводности на отрезке. Пример.1. Постройте явную разностную схему для следующей начально-краевой задачи на отрезке x [0, 1]: u t = u + x, 0 6 задаче с однородными граничными условиями: v t = v, 0 7 Итак, первый вариант явной разностной схемы для задачи.1, обладающей погрешностью аппроксимации O +, имеет вид: y j = yj 1 yj + yj +1 + x, = 1. 1, j = 0, 1. M 1, y 0 3πx = sn, = 0, 1. 4 y j 0 = 0, y j yj 1 = t j, j = 0, 1. M. Рассмотрим алгоритм решения системы.4. При j = 0 значения y j известны из начального условия. Следовательно, при каждом фиксированном j = 0, 1. M 1 неизвестными являются. Найти их можно следующим образом: 1 при = 1. 1 из первого уравнения системы.4 находим = y j + y j +1 yj + yj 1 + x ; при = 0 и = пользуемся граничными условиями, учитывая, что 1 и 1 уже известны: 0 = 0, = yj t j+1; 3 переходим на новый слой по времени, увеличивая j на единицу и повторяем действия 1 и. На рис.4-6 приведены результаты решения системы.4 для = 50 и M = Рис. 4: Аналитическое решение задачи.1. Если мы хотим, чтобы явная схема аппроксимировала исходную задачу с погрешностью O +, то можно использовать тот же прием, который применялся ранее для ап- 7
8 Рис. 5: Численное решение задачи.1 с помощью явной схемы. Рис. 6: Погрешность численного решения задачи.1 с помощью явной схемы. проксимации граничного условия, содержащего производную, в краевой задаче для обыкновенного дифференциального уравнения на отрезке. Пусть ux, t решение задачи.1. Рассмотрим выражение: u x = ux, t ux, t ux, t = ux, t + O = x x ux, t = ux, t x + O. x t Заменяя в нем производную u t конечной разностью: ux, t t = ux, t ux, t + O, 8
9 получим ux, t ux, t = ux, t x ux, t ux, t x + O +. Переходя в полученном равенстве к пределу при x 1 и учитывая, что по условию u x = t, x=1 находим, что при t = t j+1 имеет место равенство: u j+1 uj+1 1 = t j+1 u j+1 uj 1 + O +. Следовательно, разностное уравнение yj+1 1 = t j+1 yj 1.5 аппроксимирует граничное условие Неймана при x = 1 с погрешностью O +. Таким образом, меняя в схеме.4 уравнение.3 на.5, мы получим схему, аппроксимирующую исходную задачу на ее решении с погрешностью O +. Уравнение.5 удобно переписать в виде: 1 = t j yj, j = 0, 1. M 1, и использовать при уже найденных 1, yj для завершения перехода на слой j + 1. Результаты расчетов по соответствующей явной схеме на той же сетке, что и в предыдущем случае, приведены на рис Рис. 7: Численное решение задачи с помощью явной схемы с граничным условием.5. 9
10 Рис. 8: Погрешность решения задачи с помощью явной схемы с граничным условием.5. Также для получения схемы, имеющей погрешность аппроксимации O +, можно аппроксимировать граничное условие Неймана при x = 1 с помощью трехточечной первой разностной производной: 3 4yj yj+1 Переписывая это уравнение в виде = t j+1, j = 0, 1. M 1. = 4 3 yj yj+1 + t j+1 3,.6 мы можем использовать его для завершения перехода на слой j + 1 при уже найденных 1 и yj+1. Погрешность вычислений по схеме с условием.6 приведена на рис. 9. Рис. 9: Погрешность решения задачи с помощью явной схемы с граничным условием.6. 10
11 Пример.. Постройте чисто неявную разностную схему для начально-краевой задачи.1. Сравните численное решение с аналитическим и исследуйте зависимость погрешности от шагов сетки. Решение. Используем ту же сетку, что и в предыдущем примере с той лишь разницей, что соотношение шагов и теперь может быть любым. Разностная аппроксимация уравнения в соответствии с неявной схемой имеет вид: y j = yj+1 1 yj x, = 1. 1, j = 0, 1. M 1..7 Дополним разностное уравнение.7 начальными и граничными условиями на сетке. Как и в случае явной схемы, начальное условие и граничное условие Дирихле при x = 0 аппроксимируются точно: y 0 3πx = sn, = 0, 1. ; 0 = 0, j = 1. M 1. Для аппроксимации граничного условия при x = 1 используем те же три способа, что и в случае явной схемы, разобранной в предыдущем примере. Первый вариант аппроксимации граничного условия Неймана при x = 1: yj+1 1 = t j+1, j = 1. M 1. Получающаяся при этом неявная разностная схема: y 0 3πx = sn, = 0, 1. 0 = 0, j = 0, 1. M 1, y j yj+1 1 = yj+1 1 yj x, = 1. 1, j = 0, 1. M 1, = t j+1, j = 0, 1. M 1.8 имеет погрешность аппроксимации O +. Значения сеточной функции y j на нулевом слое по времени известны из начального условия, поэтому при каждом фиксированном j = 0, 1. M 1 неизвестными являются. Система уравнений, которым они удовлетворяют, имеет вид: 0 = 0, yj = yj t j+1, + yj+1 +1 = y j + x, = 1. 1,.9 11
12 то есть является системой с трехдиагональной матрицей: 0 = κ µ 1, A 1 C + B +1 = F, = 1. 1, = κ 1 + µ,.10 где κ 1 = 0, µ 1 = 0, A = B =, C = 1 +, F = y j + x, κ = 1, µ = t j+1. Очевидно, что достаточные условия устойчивости прогонки: A > 0, B > 0, C A + B, C A + B, = 1. 1, 0 κ p 1, p = 1, для системы.9 выполнены. Решая систему.9 методом прогонки и последовательно увеличивая значения j на единицу, мы полностью решим систему.8. Результаты вычислений по неявной схеме.8 в случае = M = 50 приведены на рис Рис. 10: Численное решение задачи.1 с помощью неявной схемы.8. Рис. 11: Погрешность численного решения задачи.1 с помощью неявной схемы.8. 1
13 Второй вариант аппроксимации граничного условия Неймана при x = 1: 1 = t j yj, j = 0, 1. M В этом случае для неизвестных при каждом фиксированном j получаем трехдиагональную систему вида.10, где κ = 1 1 +, µ = κ t j yj Погрешность расчетов по соответствующей неявной схеме в случае = M = 50 приведена на рис. 1.. Рис. 1: Погрешность решения задачи.1 с помощью неявной схемы с граничным условием.11. Третий вариант аппроксимации граничного условия Неймана при x = 1: = 4 3 yj yj+1 + t j+1 3 Для того, чтобы получить для неизвестных.1 систему с трехдиагональной матрицей при каждом фиксированном j, исключим из уравнения.1 неизвестное. Для этого воспользуемся уравнением.7 при = 1: yj yj yj+1 = F 1. Следовательно, = + 1 yj+1 F 1, 13
14 и уравнение.1 принимает вид: = 1 В результате для неизвестных.10, где κ = 1, 1 + F 1 + t j+1. приходим к системе с трехдиагональной матрицей вида µ = F 1 + t j+1. Погрешность расчетов по соответствующей схеме в случае = M = 50 приведена на рис. 13. Рис. 13: Погрешность численного решения задачи.1 с помощью неявной схемы с граничным условием.1. Пример.3. Постройте симметричную разностную схему схему с весом σ = 0.5 для начально-краевой задачи.1. Сравните численное решение с аналитическим и исследуйте зависимость погрешности от шагов сетки. Решение. Аппроксимация уравнения u t = u x + x в соответствии с симметричной разностной схемой имеет вид: y j = 1 y j+1 1 yj yj 1 yj + yj +1 + x,.13 где = 1. 1, j = 0, 1. M 1. Разностное уравнение.13 аппроксимирует исходное дифференциальное уравнение теплопроводности с погрешностью O + на всех внутренних узлах сетки. 14
15 Начальное условие и условие Дирихле при x = 0 аппроксимируются так же, как и в двух рассмотренных ранее случаях. Граничное условие Неймана при x = 1 можно аппроксимировать как с первым, так и со вторым порядком по. Если в качестве аппроксимации условия при x = 1 берется разностное уравнение yj+1 1 = t j+1, j = 1. M 1, то схема будет иметь погрешность аппроксимации O +. Соответствующая система для неизвестных будет трехдиагональной: 0 = 0, A 1 C + B +1 = F, = 1. 1, = yj t j+1,.14 где A = B =, C = 1 + A, F = y j + x + yj 1 yj + yj +1. Достаточные условия устойчивости прогонки для системы.14 выполнены. Погрешность решения задачи по схеме.14 для = M = 50 приведена на рис. 14. Рис. 14: Погрешность численного решения задачи.1 с помощью симметричной схемы. Построим аппроксимацию граничного условия Неймана при x = 1 с погрешностью O +. Рассмотрим равенство: ux, t ux, t = ux, t x ux, t t x + O,.15 где ux, t решение исходной задачи.1. Положим в равенстве.15 t = t j Так как ux, t j ux, t j =
16 и получаем: 1 = 1 u j uj 1 + uj+1 ux, tj ux, t j ux, t t t=tj +0.5 u j+1 1 = ux, t x + ux, t j+1 ux, t j+1 + O = ux, t j+1 ux, t j x,t j O, u j+1 u j x + O +. Перейдем в полученном равенстве к пределу при x 1 то есть при, учитывая граничные условия задачи: 1 u j uj 1 + uj+1 uj = t j Следовательно, разностное уравнение y j yj 1 + yj+1 yj+1 1 = t j +0.5 будет аппроксимировать условие u x = t x=1 yj u j+1 uj с погрешностью O +. Соответствующая система для вид: где 0 = 0, 1 1 A 1 C + B +1 = F, = 1. 1, = κ 1 + µ, 1 κ = 1 +, µ = κ 1 + yj + O +., j = 0, 1. M 1.16 при фиксированном j имеет + t j + y j + yj Погрешность, получаемая при численном решении задачи с использованием граничного условия.16, для = M = 50 приведена на рис. 15. Такой же порядок погрешности аппроксимации можно получить, используя граничное условие = 4 3 yj yj+1 + t j Исключим из этого уравнения неизвестное, используя уравнение.13 при = 1: Так как yj yj+1 = F 1. = + 1 yj+1 F 1, 16
17 Рис. 15: Погрешность численного решения задачи.1 с помощью симметричной схемы с граничным условием.16. уравнение.18 можно переписать в виде: = F 1 + t j+1. В результате мы снова придем к системе с трехдиагональной матрицей вида.17 для неизвестных при каждом фиксированном j = 0, 1. M 1, где теперь κ = 1, µ = F 1 + t j+1. Погрешность решения по предложенной схеме при = M = 50 приведена на рис. 16. Рис. 16: Погрешность решения задачи с помощью симметричной схемы с граничным условием
18 3 Задачи для самостоятельного решения Решите аналитически и численно при помощи явной, неявной и симметричной схем начальнокраевую задачу для уравнения теплопроводности на отрезке: u t = u a + fx, t, x 0, l, t 0, T ], x ux, 0 = u 0 x, u γ 0 x + δ 0u = g 0 t, x=0 u γ 1 x + δ 1u = g 1 t, x=l где: x а a =, f = cos e t, u 0 = π x, γ 0 = 1, δ 0 = 0, γ 1 = 0, δ 1 = 1, g 0 = 1, g 1 = 0, l = π; б a = 1, f = e t x / 1, u 0 = 1 + e t x /, γ 0 = 1, δ 0 = 0, γ 1 = 1, δ 1 = 0, g 0 = 0, g 1 = e t, l = 1; в a = 0.5, f = e t, u 0 = 1 + sn 3x, γ 0 = 0, δ 0 = 1, γ 1 = 1, δ 1 = 0, g 0 = e t, g 1 = 0, l = π/; 3πx г a = 1, f = 0, u 0 = 3 x + cos, γ 0 = 1, δ 0 = 0, γ 1 = 0, δ 1 = 1, g 0 = 1, g 1 = 1, l = ; 4 д a = 0.1, f = 0, u 0 = cosπx + x + x, γ 0 = 1, δ 0 = 0, γ 1 = 1, δ 1 = 0, g 0 = 1, g 1 = 5, l =. Сравните результаты численного решения по разным схемам между собой и с аналитическим решением задачи. 18
Видео:Решение задачи теплопроводности (Явная разностная схема)Скачать

Контрольная работа: Конечно-разностный метод решения для уравнений параболического типа
| Название: Конечно-разностный метод решения для уравнений параболического типа Раздел: Рефераты по математике Тип: контрольная работа Добавлен 23:16:39 16 апреля 2011 Похожие работы Просмотров: 16037 Комментариев: 20 Оценило: 3 человек Средний балл: 5 Оценка: неизвестно Скачать | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| xi | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 |
| ti | |||||||||||
| 0 | 0 | 1.1180 | 1.5388 | 1.1180 | 0.3633 | 0 | 0.3633 | 1.1180 | 1.5388 | 1.1180 | 0 |
| 0.01 | 0 | 0.6169 | 0.9288 | 0.8621 | 0.6177 | 0.4905 | 0.6177 | 0.8621 | 0.9288 | 0.6169 | 0 |
| 0.02 | 0 | 0.3942 | 0.6480 | 0.7186 | 0.6800 | 0.6488 | 0.6800 | 0.7186 | 0.6480 | 0.3942 | 0 |
| 0.03 | 0 | 0.2887 | 0.5067 | 0.6253 | 0.6665 | 0.6733 | 0.6665 | 0.6253 | 0.5067 | 0.2887 | 0 |
| 0.04 | 0 | 0.2331 | 0.4258 | 0.5560 | 0.6251 | 0.6458 | 0.6251 | 0.5560 | 0.4258 | 0.2331 | 0 |
| 0.05 | 0 | 0.1995 | 0.3720 | 0.4996 | 0.5754 | 0.6002 | 0.5754 | 0.4996 | 0.3720 | 0.1995 | 0 |
| 0.06 | 0 | 0.1759 | 0.3315 | 0.4511 | 0.5253 | 0.5504 | 0.5253 | 0.4511 | 0.3315 | 0.1759 | 0 |
| 0.07 | 0 | 0.1574 | 0.2981 | 0.4082 | 0.4778 | 0.5015 | 0.4778 | 0.4082 | 0.2981 | 0.1574 | 0 |
| 0.08 | 0 | 0.1419 | 0.2693 | 0.3698 | 0.4338 | 0.4558 | 0.4338 | 0.3698 | 0.2697 | 0.1419 | 0 |
| 0.09 | 0 | 0.183 | 0.2437 | 0.3351 | 0.3936 | 0.4137 | 0.3936 | 0.3351 | 0.2437 | 0.1283 | 0 |
| 0.1 | 0 | 0.1161 | 0.2208 | 0.3038 | 0.3570 | 0.3753 | 0.3570 | 0.3038 | 0.2208 | 0.1161 | 0 |
Величины, полученные методом Кранка-Николсона, достаточно близки к
аналитическому решению u(x,t) = sin(πx)e -π2 t + sin(3πx)e -9π2 t , истинные значения для последнего представлены в таблице 2
Максимальная погрешность для данных параметров равна 0,005
Таблица 2 – точные значения u(х i , ti ), при t=0.1
| xi | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 |
| t11 | |||||||||||
| 0.1 | 0 | 0.1153 | 0.2192 | 0.3016 | 0.3544 | 0.3726 | 0.3544 | 0.3016 | 0.2192 | 0.1153 | 0 |
Рисунок 5 –Решениеu= u(х i , ti ), для метода Кранка-Николсона
В зависимости от формы области, краевых условий, коэффициентов исходного уравнения метод конечных разностей имеет погрешности аппроксимации от первого до четвертого порядка относительно шага. В силу этого они успешно используются для разработки программных комплексов автоматизированного проектирования технических объектов.
В МКР строятся, как правило, регулярные сетки, особенности геометрии области учитываются только в около граничных узлах. В связи с этим МКР чаще применяется для анализа задач с прямолинейными границами областей определения функций.
Проблемой методов конечных разностей является высокая размерность результирующей системы алгебраических уравнений (несколько десятков тысяч в реальных задачах. Поэтому реализация методов конечных разностей в составе САПР требует разработки специальных способов хранения матрицы коэффициентов системы и методов решения последней.
1 Березин И.С., Жидков Н.П. Методы вычислений. Т.2. – М.: Физматгиз, 1962.
2 Мэтьюз, Джон, Г., Финк, Куртис, Д. Численные методы. Использование MATLAB, 3-е издание.— М. : Вильяме, 2001. — 720 с
3 Тихонов А.Н., Самарский А.А. Уравнения математической физики. – М.: Наука, 1972.
4 Формалев В.Ф., Ревизников Д.Л. Численные методы. – М.: ФИЗМАТЛИТ, 2004. — 400 с.
5 Пирумов У.Г. Численные методы. – М.: Издательство МАИ, 1998.
6 Калиткин Н.Н. Численные методы. – М.: Наука, 1976.
Листинг программы для расчета по методу Кранка-Николсона
Видео:Лекция №1.1 Явная и неявная схемы для уравнения теплопроводностиСкачать

Уравнение теплопроводности
Ранее (см. разд. 2.1.2, 2.1.3) уже были построены и исследованы разностные схемы решения смешанной задачи для одномерного уравнения теплопроводности:

Были получены две двухслойные схемы — явная (2.3) и неявная (2.4). В явной схеме значения сеточной функции 
Неявная схема безусловно устойчива, явная схема устойчива при выполнении условия
Обе схемы сходятся к решению исходной задачи со скоростью 
Схемы (2.3), (2.4) построены для случая, когда значения искомой функции (температуры) Uна границах х = 0, х = 1определяются заданными функциями 
В этом случае, как и при решении волнового уравнения, данное условие нужно записывать в схемах (2.3), (2.4) в разностном виде.
Перейдем теперь к построению разностных схем для уравнения теплопроводности с двумя пространственными переменными. Примем для простоты а = 1. Тогда это уравнение можно записать в виде

Пусть при t=0 начальное условие задано в виде

В отличие от волнового уравнения, требующего два начальных условия, в уравнение теплопроводности входит только первая производная по t, и необходимо задавать одно начальное условие.
Часто задачи теплопроводности или диффузии, описываемые двумерным уравнением (2.76), решаются в ограниченной области. Тогда, кроме начального условия (2.77), нужно формулировать граничные условия. В частности, если расчетная область представляет прямоугольный параллелепипед 


Рис. 2.24. Расчетная область
Введем простейшую сетку с ячейками в виде прямоугольных параллелепипедов, для чего проведем три семейства плоскостей: хi= ih1(i=0,1. I), 



Рассмотренные выше схемы для одномерного уравнения легко обобщаются на двумерный случай.
Построим явную разностную схему, шаблон которой изображен на рис. 2.25. Аппроксимируя производные отношениями конечных разностей, получаем следующее сеточное уравнение:
Рис. 2.25. Шаблон двумерной схемы
Отсюда можно найти явное выражение для значения сеточной функции на (k + 1)-ом слое:

Условие устойчивости имеет вид

При 

Полученная схема сходится со скоростью
Формулы (2.78) или (2.80) представляют собой рекуррентные соотношения для последовательного вычисления сеточной функции во внутренних узлах слоев k = 1,2. К. На нулевом слое используется начальное условие (2.77), которое записывается в виде

Значения 
Алгоритм решения смешанной задачи для двумерного уравнения теплопроводности изображен на рис. 2.26. Здесь решение хранится на двух слоях: нижнем (массив 

Рис. 2.26. Алгоритм решения двумерного уравнения теплопроводности
Построим теперь абсолютно устойчивую неявную схему для решения уравнения (2.76), аналогичную схеме (2.4) для одномерного уравнения теплопроводности. Аппроксимируя в (2.76) вторые производные по пространственным переменным на (k + 1)-ом слое, получаем следующее разностное уравнение:

Это уравнение можно записать в виде системы линейных алгебраических уравнений относительно значений сеточной функции на каждом слое:

К этой системе уравнений нужно добавить граничные условия для определения значений сеточной функции в граничных узлах (т.е. при i= 0, I; j = 0, J). На нулевом слое решение находится из начального условия (2.77), представленного в виде (2.81).
Система (2.83), полученная для двумерного уравнения теплопроводности, имеет более сложный вид, чем аналогичная система (2.22) для одномерного случая, которую можно решить методом прогонки. Таким образом, распространение неявной схемы на многомерный случай приводит к значительному усложнению вычислительного алгоритма и увеличению объема вычислений.
Недостатком явной схемы (2.78) является жесткое ограничение на шаг по времени τ, вытекающее из условия (2.79). Существуют абсолютно устойчивые экономичные разностные схемы, позволяющие вести расчет со сравнительно большим значением шага по времени 
🔍 Видео
Решение уравнения теплопроводности в одномерной постановке в Excel с применением неявной схемыСкачать

3_06. Порядок аппроксимации.Скачать

Решение уравнения теплопроводности методом конечных разностейСкачать

Метод Фурье для неоднородного уравнения теплопроводностиСкачать

Уравнение в частных производных Уравнение теплопроводностиСкачать

Приклонский В. И. - Численные методы в физике - Лекция 16Скачать

Решение первой начально-краевой задачи для одномерного уравнения теплопроводности.Скачать

Приклонский В. И. - Численные методы в физике - Дополнение к лекциямСкачать

Вывод уравнения теплопроводностиСкачать

Решение задачи Коши для уравнения теплопроводности (Часть 1)Скачать

8.1 Решение уравнения теплопроводности на отрезкеСкачать

Тихонов Н. А. - Основы математического моделирования - Метод конечных разностей (Лекция 7)Скачать

Решение задач теплопроводности (короткая версия)Скачать

Решение уравнения теплопроводности в одномерной постановке в ExcelСкачать

Вычислительная математика 17 Теория разностных схемСкачать

Кобельков Г. М. - Численные методы. Часть 2. Семинары - Лекция 4Скачать

Уравнения математической физики 11 Формула Пуассона для уравнения теплопроводностиСкачать

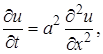
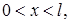
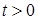 (1)
(1)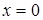 и
и 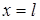 заданы значения искомой функции
заданы значения искомой функции 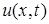 в виде
в виде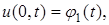
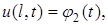
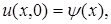
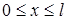 ,
, 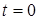 , (4)
, (4)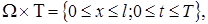 a 2 — коэффициент температуропроводности, а (2), (3) с помощью функций
a 2 — коэффициент температуропроводности, а (2), (3) с помощью функций 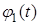 ,
, 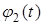 задают температуру на границах
задают температуру на границах 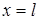 заданы значения производных искомой функции по пространственной переменной:
заданы значения производных искомой функции по пространственной переменной: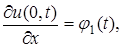
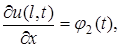
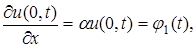
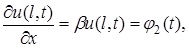
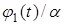 на границе
на границе 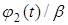 на границе
на границе 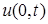 ,
, 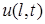 . Коэффициенты α, β – известные коэффициенты теплообмена между газообразной или жидкой средой и соответствующей границей.
. Коэффициенты α, β – известные коэффициенты теплообмена между газообразной или жидкой средой и соответствующей границей.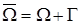 первая начально-краевая задача имеет вид
первая начально-краевая задача имеет вид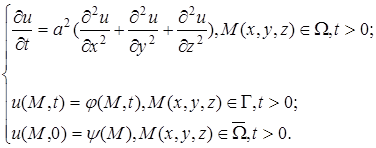 (9)
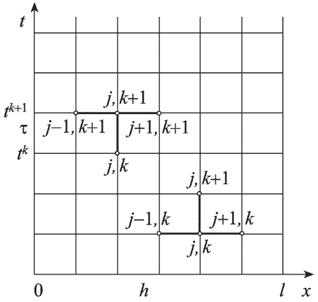
(9)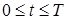 конечно разностную сетку ωh,τ :
конечно разностную сетку ωh,τ :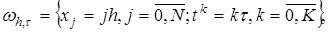 (10)
(10)
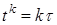 ,на котором распределение искомой функции u ( xj , t k ) ,
,на котором распределение искомой функции u ( xj , t k ) , 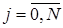 , известно (при к = 0 распределение определяется начальным условием (4)u ( xj , t k )=ψ( xj ) ), и верхний временной слой t k +1 =( k +1) τ , на котором распределение искомой функции u ( xj , t k +1 ) ,
, известно (при к = 0 распределение определяется начальным условием (4)u ( xj , t k )=ψ( xj ) ), и верхний временной слой t k +1 =( k +1) τ , на котором распределение искомой функции u ( xj , t k +1 ) , 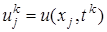 .
.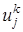 ,
, 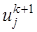 первая из которых известна, вторая подлежит определению. Для определения в задаче (1)-(4) заменяют (аппроксимируют) дифференциальные операторы отношением конечных разностей (более подробно это рассматривают в разделах численных методов «Численное дифференцирование»), получают
первая из которых известна, вторая подлежит определению. Для определения в задаче (1)-(4) заменяют (аппроксимируют) дифференциальные операторы отношением конечных разностей (более подробно это рассматривают в разделах численных методов «Численное дифференцирование»), получают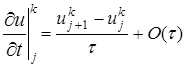 , (11)
, (11)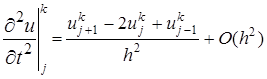 , (12)
, (12)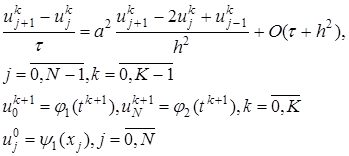 (13)
(13)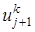 , которое может быть определено явно из соотношений (13). В соотношения (13) краевые условия входят при значениях j =1 и j = N — l , a начальное условие – при k = 0.
, которое может быть определено явно из соотношений (13). В соотношения (13) краевые условия входят при значениях j =1 и j = N — l , a начальное условие – при k = 0.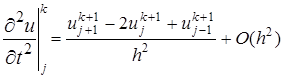 , (14)
, (14)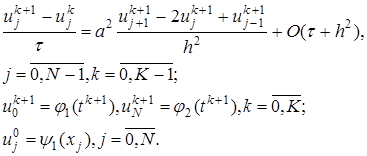 (15)
(15)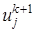 на верхнем временном слое можно получить из решения (15) с трехдиагональной матрицей. Эта СЛАУ в форме, пригодной для использования метода прогонки, имеет вид
на верхнем временном слое можно получить из решения (15) с трехдиагональной матрицей. Эта СЛАУ в форме, пригодной для использования метода прогонки, имеет вид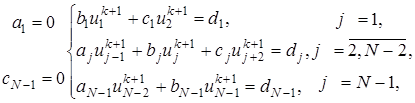
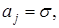
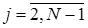 ;
;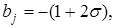
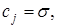 ,
, 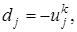
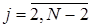 ;
;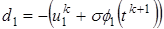 ;
;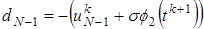 ;
;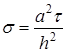 .
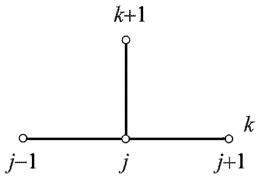
.
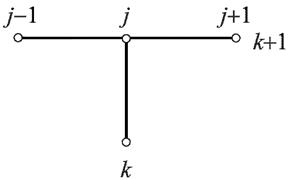
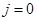 , чтобы в дальнейшем последовательно определять значения решения в узлах слоев
, чтобы в дальнейшем последовательно определять значения решения в узлах слоев 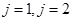 и т.д. В случае второй схемы, которая является неявной, обязательно приходится решать систему уравнений для нахождения решения сеточной задачи. В любом случае согласно методу сеток будем иметь столько уравнений, сколько имеется неизвестных (значения искомой функции в узлах). Число неизвестных равно числу всех узлов сетки. Решая систему уравнений, получаем решение поставленной задачи.
и т.д. В случае второй схемы, которая является неявной, обязательно приходится решать систему уравнений для нахождения решения сеточной задачи. В любом случае согласно методу сеток будем иметь столько уравнений, сколько имеется неизвестных (значения искомой функции в узлах). Число неизвестных равно числу всех узлов сетки. Решая систему уравнений, получаем решение поставленной задачи.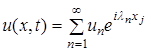 , (16)
, (16)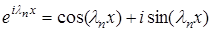 – собственные значения функции, получаемые из решения соответствующей задачи Штурма-Лиувиля, т.е. решение может быть представлено в виде суперпозиции отдельных гармоник
– собственные значения функции, получаемые из решения соответствующей задачи Штурма-Лиувиля, т.е. решение может быть представлено в виде суперпозиции отдельных гармоник 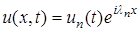 , каждая из которых есть произведение функции времени и функции пространственной переменной, причем последняя по модулю ограничена сверху единицей при любых значениях переменной x .
, каждая из которых есть произведение функции времени и функции пространственной переменной, причем последняя по модулю ограничена сверху единицей при любых значениях переменной x .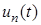 , называемая амплитудной частью гармоники, никак не ограничена, и, по всей вероятности, именно амплитудная часть гармоник является источником неконтролируемого входными данными роста функции и, следовательно, источником неустойчивости.
, называемая амплитудной частью гармоники, никак не ограничена, и, по всей вероятности, именно амплитудная часть гармоник является источником неконтролируемого входными данными роста функции и, следовательно, источником неустойчивости.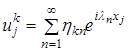 (17)
(17)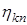 может быть представлена в виде произведения
может быть представлена в виде произведения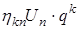 (18)
(18)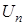 – размерный и постоянный сомножитель амплитудной части,
– размерный и постоянный сомножитель амплитудной части,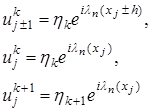 (19)
(19)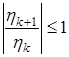 , (20)
, (20)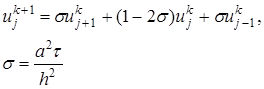 (21)
(21)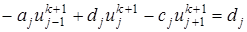 (22)
(22)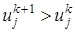 . Тогда, в соответствии с явной схемой (21), разностное решение будет заниженным по сравнению с точным, так как
. Тогда, в соответствии с явной схемой (21), разностное решение будет заниженным по сравнению с точным, так как 
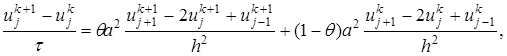 (23)
(23)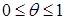 . При θ=1 имеем полностью неявную схему, при θ=0 – полностью явную схему, а при θ=1/2 – схему Кранка-Николсона .
. При θ=1 имеем полностью неявную схему, при θ=0 – полностью явную схему, а при θ=1/2 – схему Кранка-Николсона .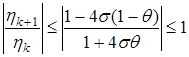 ,
,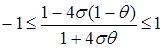 (24)
(24)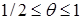 . Если же вес θ лежит в пределах
. Если же вес θ лежит в пределах 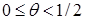 , то между σ и θ из левого неравенства устанавливается связь
, то между σ и θ из левого неравенства устанавливается связь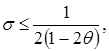
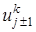 ,
, 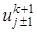 по переменной х и полученные разложения подставим в (23):
по переменной х и полученные разложения подставим в (23):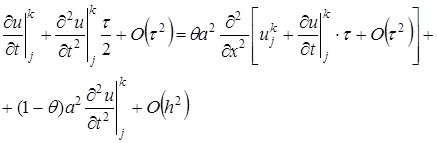
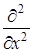 от квадратной скобки в соответствии с дифференциальным уравнением равен дифференциальному оператору
от квадратной скобки в соответствии с дифференциальным уравнением равен дифференциальному оператору 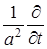 , в соответствии с чем вышеприведенное равенство приобретает вид
, в соответствии с чем вышеприведенное равенство приобретает вид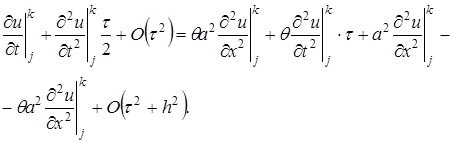
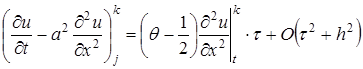 ,
,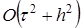 , т.е. на один порядок по времени выше, чем для обычных явных или неявных схем. Таким образом, схема Кранка-Николсона при θ = 1/2 абсолютно устойчива и имеет второй порядок аппроксимации по времени и пространственной переменной х .
, т.е. на один порядок по времени выше, чем для обычных явных или неявных схем. Таким образом, схема Кранка-Николсона при θ = 1/2 абсолютно устойчива и имеет второй порядок аппроксимации по времени и пространственной переменной х .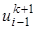 ,
, 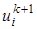 , и
, и 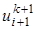 . Это возможно, если все значения перенести в левую часть уравнения. Затем упорядочим члены уравнения (23) и в результате получим неявную разностную формулу
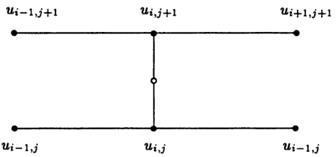
. Это возможно, если все значения перенести в левую часть уравнения. Затем упорядочим члены уравнения (23) и в результате получим неявную разностную формулу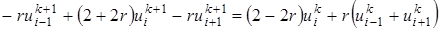 (26)
(26)
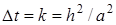 , формула (26) упрощается и принимает вид
, формула (26) упрощается и принимает вид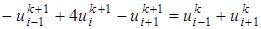 , (27)
, (27)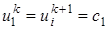 и
и 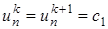 соответственно).
соответственно).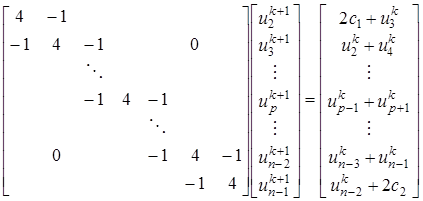
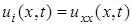 ,
,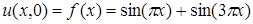 ,
,