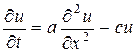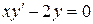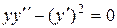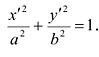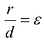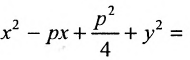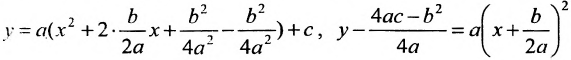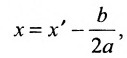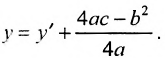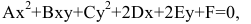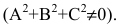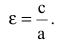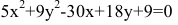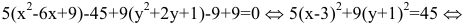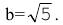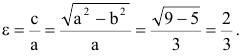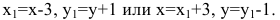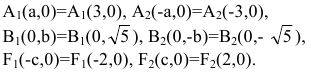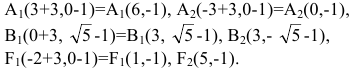Основные понятия и определения
В математике и ее приложениях часто возникает задача отыскания неизвестной функции. Один из основных приемов решения такой задачи – составление уравнения относительно этой функции. Во многих случаях эти уравнения содержат не только саму искомую функцию, но и ее производные или дифференциалы. Такого рода уравнения называют дифференциальными уравнениями.
Пример.
Тело массы т падает вертикально вниз с некоторой высоты. Требуется установить зависимость скорости падения от времени, если на тело, кроме силы тяжести, действует сила сопротивления воздуха (тормозящая сила), пропорциональная величине скорости.
Пусть 




С другой стороны, в силу второго закона Ньютона 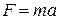

Используя равенство 


Таким образом, исходная задача свелась к чисто математической задаче:
«Найти функцию 


Определение 23.1 Дифференциальным уравнением называется уравнение, связывающее независимые переменные, искомую функцию, и её производные (или дифференциалы) различных порядков. Порядок старшей производной неизвестной функции, входящей в данное дифференциальное уравнение, называется порядкомэтого уравнения.
Если неизвестная функция зависит от одной переменной, то дифференциальное уравнение называется обыкновенным. Если неизвестная функция есть функция нескольких переменных, и дифференциальное уравнение содержит частные производные этой функции, то его называют уравнением в частных производных.
Например, 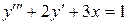

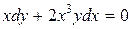



есть дифференциальные уравнения второго порядка в частных производных относительно функции 
В дальнейшем будем рассматривать только обыкновенные дифференциальные уравнения.
В общем виде обыкновенное дифференциальное уравнение п-го порядка можно представить в виде

где х – независимая переменная, у = 

то говорят, что оно разрешено относительно старшей производной или записано в нормальной форме.
Определение 23.2 Решением дифференциального уравнения п-го порядка называется всякая функция 

Например, функции 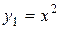

для любого х. Действительно, поскольку 
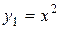




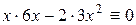
Функции 

Операция отыскания всех решений дифференциального уравнения в некоторой области изменения независимой переменной называется интегрированием дифференциального уравнения.


Например, функция 





следовательно, 
Основная задача теории дифференциальных уравнений состоит в нахождении всех решений заданного уравнения и изучении их свойств.
Дифференциальные уравнения первого порядка
Дифференциальное уравнение первого порядка имеет вид
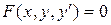
Будем рассматривать только такие дифференциальные уравнения, которые можно записать в нормальной форме
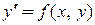
Часто используется также следующая форма записи дифференциального уравнения первого порядка:

Указанные формы записи уравнений первого порядка тождественны в том смысле, что от одной из них с помощью тождественных преобразований и замены 




Рассмотрим простейшее дифференциальное уравнение первого порядка

Нахождение решений этого дифференциального уравнения составляет знакомую нам основную задачу интегрального исчисления – отыскание первообразных функции 
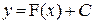

В то же время, при решении прикладных задач, приводящих к дифференциальным уравнениям относительно некоторой функции 




и называют начальными условиями, а величины у0 и х0 при этом называются начальными значениями.
Если дифференциальное уравнение описывает некоторый реальный процесс (физический, химический, природный, социальный и т.д.), то начальные условия (1.3), чаще всего, определяют начальное состояние этого процесса.
Определение 23.3Задача отыскания решения дифференциального уравнения 

Геометрически задача Коши состоит в отыскании той интегральной кривой, которая проходит через заданную точку 
В связи с этим, возникает еще один вопрос: для любых ли начальных условий 
Справедлива следующая теорема существования и единственности решения задачи Коши для дифференциального уравнения первого порядка.
Если в дифференциальном уравнении 

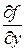


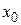

Геометрический смысл теоремы Коши состоит в следующем: через каждую точку 
Таким образом, теорема Коши отвечает на оба поставленных нами вопроса:
1. В области D непрерывности функции 
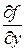


2. Для любого начального условия 

Таким образом, по виду правой части уравнения 

Пусть D – область плоскости Оху, в которой выполнены условия теоремы Коши.
Определение 23.4 Общим решением дифференциального уравнения 

1) 
2) для всякого начального условия 


Общее решение, записанное в неявном виде Ф(х, у, С) = 0, называют общим интегралом дифференциального уравнения.
Геометрически общее решение определяет в области D семейство интегральных кривых.
Определение 23.5 Частным решением дифференциального уравнения 

Геометрически частное решение определяет одну кривую семейства интегральных кривых. Таким образом, задача Коши – это задача отыскания частного решения заданного дифференциального уравнения, удовлетворяющего заданным начальным условиям.
Если известно общее решение 

1. В равенстве 
3. Подставляют найденное значение 

4. Полученная функция 
Заметим, что теорема Коши гарантирует единственность решения только для точек 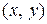

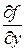









Определение 23.6Точки (х0, у0), в окрестности которых решение дифференциального уравнения, удовлетворяющее условию 
Очевидно, для уравнения 

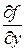

Может случиться и так, что дифференциальное уравнение имеет решение, которое ни при каких значениях константы С из общего решения не получается.
Например, для уравнения 






этой прямой – особые.
Решение дифференциального уравнения, график которого состоит сплошь из особых точек, называют особым решением, а соответствующую интегральную кривую называют особой кривой данного дифференциального уравнения. Особое решение не может быть получено из общего решения дифференциального уравнения ни при каком значении постоянной С.
В общем случае, решить дифференциальное уравнение – значит найти все его решения, т.е. общее решение (общий интеграл) и особые решения, если они существуют. В данном пособии мы будем рассматривать только вопрос нахождения общего решения дифференциальных уравнений.
1.3 Геометрическая и механическая интерпретация дифференциального уравнения первого порядка
Пусть 



Следовательно, дифференциальное уравнение 

Если в каждой точке М 

Если для наглядности через каждую точку 

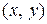




|
Например, если для некоторого дифференциального уравнения поле направлений имеет вид, изображенный на рисунке 1.2, то, очевидно, интегральные кривые этого дифференциального уравнения есть концентрические окружности с центром в начале координат.
Значит, построив поле направлений заданного дифференциального уравнения первого порядка, можно построить интегральные кривые этого уравнения.
Рассмотрим метод построения интегральных кривых, называемый методом изоклин.
Определение 23.8. Изоклиной *) дифференциального уравнения 

Из определения следует, что уравнение изоклины, соответствующей значению 
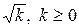
Смысл параметра 
Алгоритм метода изоклин включает следующие шаги:
1) Записать уравнения изоклин f(x, у) = k.
2) Построить изоклины, придавая k числовые значения из области значений функции 
3) Построить поле направлений. С этой целью для каждой изоклины найти угол a наклона поля направлений из условия 
4) В полученном поле направлений построить искомые интегральные кривые так, чтобы они пересекали каждую изоклину под тем углом a, который указан на этой изоклине.
Замечание 1.
При построении изоклин выделяют изоклины нулей ( 

Замечание 2.
Чтобы получить достаточно точное представление о поведении интегральных кривых, нужно построить как можно более «густое» семейство изоклин. Если требуется решить дифференциальное уравнение с начальными условиями 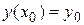
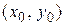

Построить отрезок под углом a к оси Ох, для которого 

Поэтому, если построить треугольник с катетами т и п, где 
Исходя из этого, поле направлений можно построить так. Взять любую расположенную вблизи изоклины вершину клетки, пусть это точка А (рисунок 1.3). Из этой точки переместиться по горизонтали на п клеточек вправо, если 

Решение. Уравнение изоклин данного ДУ 1 + у 2 = k , или 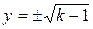


О методе изоклин построения интегральных кривых можно прочитать также в [1], гл. 13, § 3.



Учитывая физический смысл производной: 


Это дифференциальное уравнение первого порядка называют дифференциальным уравнением движения.



Задача Коши: 


Таким образом, с физической точки зрения, дифференциальное уравнение первого порядка есть дифференциальное уравнение движения точки по прямой; решение этого уравнения есть закон движения этой точки, интегральная кривая – график движения.
*) Если в каждой точке области Q задано значение некоторой величины, то говорят что в области Q задано поле этой величины.
Видео:Лекция 31.2. Кривые второго порядка. Гипербола.Скачать

Кривые второго порядка — определение и построение с примерами решения
Содержание:
Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру — значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде
- Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
- если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.
Это определение в более компактной записи выглядит следующим образом. Уравнение 
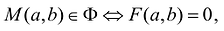
Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения 
Возможны два вида задач:
- дано уравнение
и надо построить фигуру Ф, уравнением которой является
;
- дана фигура Ф и надо найти уравнение этой фигуры.
Первая задача сводится к построению графика уравнения 
Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:
- Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
- Записать в координатах условие, сформулированное в первом пункте.
Видео:Видеоурок "Гипербола"Скачать

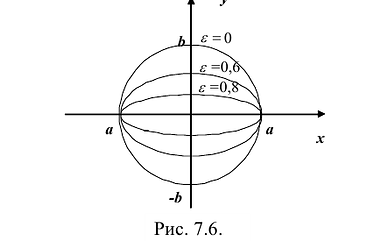
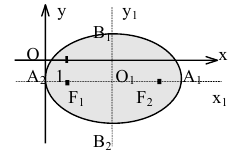
Эллипс
Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек 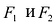
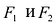
Точки 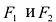
Если а =Ь, то уравнение (7.3) можно переписать в виде:
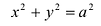
Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку 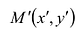
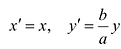
Число 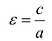
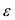
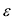
Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами 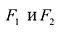
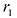
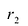
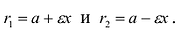
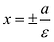
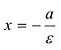
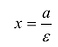
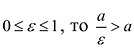
Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Гипербола
Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек 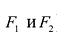
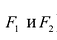
Точки 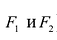
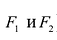
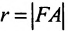
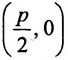
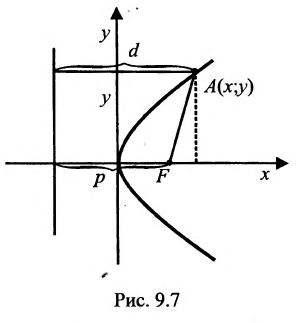
Тогда 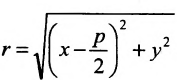
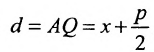
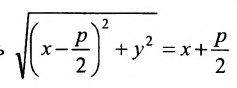
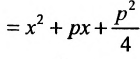
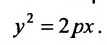
Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения 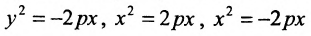
Легко показать, что уравнение 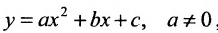
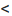
и сделаем параллельный перенос по формулам
В новых координатах преобразуемое уравнение примет вид: 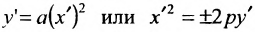
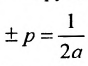
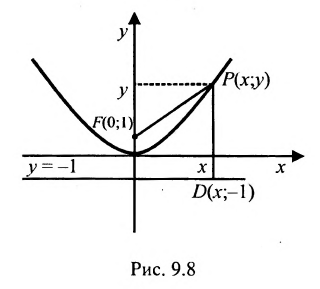
Пример:
Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию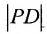
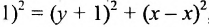
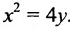
Видео:Решить дифф. уравнение и построить интегральные кривыеСкачать

Кривые второго порядка на плоскости
Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:
где коэффициенты А, В и С не равны одновременно нулю
Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.
Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.
Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению
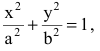
Число а называют большей полуосью эллипса, число 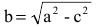
шей полуосью эллипса, 2а и 2b — соответственно большей и меньшей осями эллипса. Точки 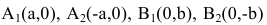
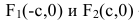
Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии. Центр симметрии эллипса называется центром эллипса.
Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.
В случае а=b каноническое уравнение эллипса принимает вид 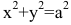
Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.
Так, в случае а>b эксцентриситет эллипса выражается формулой:
Эксцентриситет изменяется от нуля до единицы 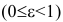
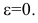
Пример:
Показать, что уравнение
является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.
Решение:
Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:
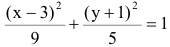
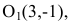
Найдем эксцентриситет эллипса:
Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке 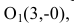
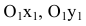
В новой системе координат координаты 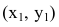
Переходя к старым координатам, получим:
Построим график эллипса.
Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.
Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Особые решения дифференциальных уравнений
Решение дифференциального уравнения
называется особым , если в каждой его точке нарушается свойство единственности, т. е. если через каждую его точку кроме этого решения проходит и другое решение, имеющее в точке ту же касательную, что и решение , но не совпадающее с ним в сколь угодно малой окрестности . График особого решения будем называть особой интегральной кривой уравнения (1). Если функция и ее частные производные и непрерывны по всем аргументам , то любое особое решение уравнения (1) удовлетворяет также уравнению
Значит, чтобы отыскать особые решения (1), надо исключить из уравнений (1) и (2).
Полученное после исключения из (1) и (2) уравнение
Часто бывает так, что распадается на несколько ветвей . Тогда нужно установить, является ли каждая в отдельности ветвь решением уравнения (1), и если является, то будет ли оно особым решением, т.е. нарушается ли единственность в каждой его точке.
Пример 1. Найти особые решения дифференциального уравнения
а) Находим p-дискриминантную кривую. В данном случае и условие (2) принимает вид , отсюда . Подставляя это выражение для в уравнение (4), получаем
Кривая (5) есть p-дискриминантная кривая уравнения (4): она состоит из одной ветви — параболы.
б) Проверяем, является ли p-дискриминантная кривая решением заданного уравнения. Подставляя (5) и ее производную в (4), убеждаемся, что есть решение уравнения (4).
в) Проверяем, является ли решение (S) особым решением уравнения (4). Для этого найдем общее решение уравнения (4). Перепишем (4) в виде . Это уравнение Клеро. Его общее решение
Выпишем условие касания двух кривых и в точке с абсциссой :
Первое равенство выражает совпадение ординат кривых, а второе выражает совпадение угловых коэффициентов касательных к этим кривым в точке с абсциссой .
Полагая , находим, что условия (7) принимают вид
Подставляя в первое из равенств (8), получаем или т.е. при первое равенство выполняется тождественно, так как есть абсцисса произвольной точки.
Итак, в каждой точке кривой (5) ее касается некоторая другая кривая семейства (6), а именно та, для которой . Значит, есть особое решение уравнения (4).
г) Геометрическое истолкование.
Общее решение уравнения (4) есть семейство прямых (6), а особое решение (5) является огибающей этого семейства прямых (рис. 19).
Огибающей семейства кривых
называется такая кривая, которая в каждой своей точке касается некоторой кривой семейства (9) и каждого отрезка которой касается бесконечное множество кривых из (9). Будем говорить, что кривые и касаются в точке , если они имеют в этой точке общую касательную.
Если (9) есть общий интеграл уравнения (1), то огибающая семейства кривых (9), если она существует, будет особой интегральной кривой этого уравнения. В самом деле, в точках огибающей значения совпадают со значениями для интегральной кривой, касающейся огибающей в точке , и, следовательно, в каждой точке огибающей значения удовлетворяют уравнению , т.е. огибающая является интегральной кривой.
Далее, в каждой точке огибающей нарушена единственность, так как через точки огибающей по одному направлению проходит, по крайней мере, две интегральные кривые: сама огибающая и касающаяся ее в рассматриваемой точке интегральная кривая семейства (9). Следовательно, огибающая является особой интегральной кривой.
Из курса математического анализа известно, что огибающая входит в состав C-дискриминантной кривой (коротко СДК), определяемой системой уравнений
Некоторая ветвь СДК заведомо будет огибающей, если на ней:
1) существуют ограниченные по модулю частные производные
где и — постоянные;
Замечание. Условия 1) и 2) лишь достаточны, а потому ветви СДК, на которых нарушено одно из этих условий, тоже могут быть огибающими.
Пример 2. Найти особые решения дифференциального уравнения
а) Находим C-дискриминантную кривую. Имеем , так что отсюда . Подставляя это значение в (14), получаем откуда
Это и есть C-дискриминантная кривая: она состоит из двух прямых и .
б) Непосредственной подстановкой убеждаемся, что каждая из ветвей СДК является решением уравнения (13).
в) Докажем, что каждое из решений (15) является особым решением уравнения (13). В самом деле, так как и , то на каждой ветви СДК имеем (предполагаем, что решение уравнения (13) рассматривается на отрезке
где — область допустимых значений .
Заметим, что на любой из ветвей СДК в области 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQCAMAAABncAyDAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMAMRDQiiHowAFBoWFRoLFx3eb7ogAAAMZJREFUKM+1UksSwyAIVUHAX+T+p602mTYkdqZd1AUL5fk+4NzfjiQvv/QXwkz++/6kyblOYfXmMd4vNxglaF//xu0KEeJZdVYXkDFUbhaSDCDqDtDhO3ASgOypGJbMyVh4A3A8bBpQq1URM1exAEcTUHaF4R5ZzFQXDE+FuDIfET4AiqZFe+PykiQHYIbb8rAgTsAM3lvTjvc5DCVeORANFjSxbhfOqn6ux5wPICRojOf2fJ81Uscj+bmEUc5q4jKCXucmPQAaYQaRCPmIUQAAAABJRU5ErkJggg==» />, так дх что выполняется одно из условий (12). Значит, условия (11) и (12) выполняются, а, следовательно, прямые (15) являются огибающими парабол (14).
Итак, установлено, что каждое из решений (15) есть особое решение.
В вопросах отыскания особых решений оказываются полезными следующие символические схемы:
Схема (16) означает, что уравнение p-дискриминантной кривой может распадаться на три уравнения:
1) — уравнение огибающей;
2) — уравнение геометрического места точек заострения (возврата);
3) — уравнение геометрического места точек прикосновения интегральных линий, причем множитель входит в в квадрате.
Схема (17) означает, что уравнение C-дискриминантной кривой может распадаться на три уравнения:
1) — уравнение огибающей;
2) — уравнение геометрического места узловых точек, причем множитель входит в в квадрате;
3) — уравнение геометрического места точек заострения, причем множитель входит в в кубе.
Не обязательно, чтобы для каждой задачи все составные части и фигурировали в соотношениях (16) и (17).
Из всех геометрических мест только огибающая есть особое решение дифференциального уравнения. Отыскание огибающей упрощается тем, что в схемы (16) и (17) она входит в первой степени.
В отношении других геометрических мест (точек заострения, узловых точек и точек прикосновения) требуется дополнительный анализ в каждом конкретном случае. То обстоятельство, что некоторый множитель входит в в квадрате (и совсем не входит в ) указывает на то, что здесь может быть геометрическое место точек прикосновения интегральных линий. Аналогично, если некоторый множитель входит в в квадрате (и совсем не входит в ), то здесь может быть геометрическое место узловых точек. Наконец, если множитель входит в в первой степени, а в — в третьей, то возможно наличие геометрического места точек заострения.
Пример 3. Найти особое решение дифференциального уравнения
Решение. Особое решение, если оно существует, определяется системой
где второе уравнение (19) получено из (18) дифференцированием его по . Исключив , получим p-дискриминантную кривую , которая распадается на две ветви
Подстановкой убеждаемся, что обе функции являются решениями уравнения (18).
Чтобы установить, являются ли решения (20) и (21) особыми или нет, найдем огибающую семейства
являющегося общим интегралом для (18).
Выпишем систему для определения C-дискриминантной кривой откуда, исключая , получаем , или и , что совпадает с (20) и (21). В силу того, что на линиях (20) и (21) условия (11) и (12) выполняются, заключаем, что линии и являются огибающими, а значит (20) и (21) есть особые решения заданного уравнения.
Интегральные кривые (22) суть параболы , а линии — огибающие этого семейства парабол (рис. 20).
Пример 4. Найти особые решения дифференциального уравнения
Решение. Дифференцируем (23) по
Исключая из (23) и (24), получим . Дискриминантная кривая есть ось ординат. Она не является интегральной кривой уравнения (23), но согласно схеме (16) может быть геометрическим местом точек прикосновения интегральных кривых.
Решениями уравнения (23) являются параболы и те гладкие кривые, которые можно составить из их частей (рис. 21).
Из чертежа видно, что прямая действительно есть геометрическое место точек прикосновения интегральных кривых уравнения (23).
Пример 5. Найти особые решения дифференциального уравнения
Решение. Найдем . Исключая из системы уравнений получаем
Преобразовав уравнение (25) к виду , находим его общий интеграл .
Найдем . Исключая из системы уравнений будем иметь
Итак, из (26) и (27) имеем
Множитель входит в p-дискриминант и в C-дискриминант в первой степени и дает огибающую, т. е. функция есть особое решение дифференциального уравнения (25). Непосредственной подстановкой убеждаемся, что действительно удовлетворяет уравнению.
Уравнение , входящее во второй степени в p-дискриминант и совсем не входящее в C-дискриминант, дает место точек прикосновения .
Наконец, уравнение , входящее в C-дискриминант во второй степени и совсем не входящее в p-дискриминант, дает место узловых точек (рис.22).
Пример 6. Найти особые решения дифференциального уравнения
а) Ищем p-дискриминантную кривую. Дифференцируя (28) по , получаем , откуда
Подставляя (29) в (28), найдем уравнение :
б) Ищем общий интеграл уравнения (28). Обозначив у’ через р, перепишем (28) в виде
Дифференцируя обе части (28) по и учитывая, что , будем иметь
Приравнивая нулю первый множитель , получаем (29), а соотношение дает
Исключая параметр из уравнений (31) и (32), найдем общее решение уравнения (28):
в) Находим C-дискриминантную кривую. Дифференцируя (33) по C, будем иметь
Подставляя (34) в (33), получаем уравнение .
Согласно символическим схемам (16) и (17) заключаем, что есть огибающая семейства полукубических парабол (33), а есть геометрическое место точек заострения (множитель входит в уравнение в кубе) (рис. 23). Подстановкой в уравнение (28) убеждаемся, что есть решение, а решением не является (при уравнение (28) не имеет смысла). Таким образом, решение есть особое (огибающая семейства интегральных линий).
🔥 Видео
Эллипс, парабола и гипербола. Конические сечения | Ботай со мной #055 | Борис Трушин |Скачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Кривые второго порядка. ГиперболаСкачать

Лекция 31.3. Кривые второго порядка. Парабола.Скачать

Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

Определить тип кривой (гипербола)Скачать
Новая задача №9 на гиперболу из ЕГЭ 2022 по математикеСкачать

Лекция 31.1. Кривые второго порядка. ЭллипсСкачать

Написать каноническое уравнение гиперболы. Дан эксцентриситетСкачать

1. Что такое дифференциальное уравнение?Скачать

7.1. Кривые второго порядка. Окружность. Эллипс. ГиперболаСкачать

Графики функций №3 ГиперболаСкачать

Тип кривой второго порядкаСкачать

Как написать уравнения касательной и нормали | МатематикаСкачать

Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать