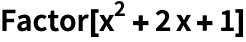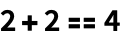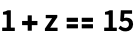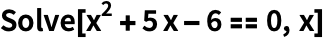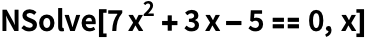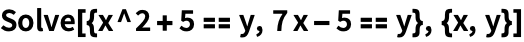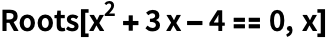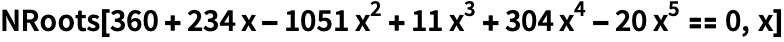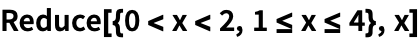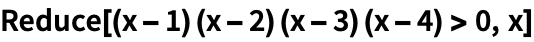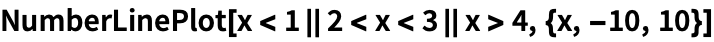Wolfram mathematica решить систему уравнений (8 видео)

Online Systems of Equations Solver

Содержание

Solve equations and systems of equations with Wolfram|Alpha
A powerful tool for finding solutions to systems of equations and constraints
Tips for entering queries
Access instant learning tools
What are systems of equations?
A system of equations is a set of one or more equations involving a number of variables.
Алгебра
7. Уравнения и системы уравнений
📹 Видео

Видео:12.01 Решение систем ДУ в Wolfram MathematicaСкачать

Solve equations and systems of equations with Wolfram|Alpha

Видео:Wolframalpha : решение любых задач для студента по алгебре, вышке, физике, дифференциальные ур. и прСкачать

A powerful tool for finding solutions to systems of equations and constraints

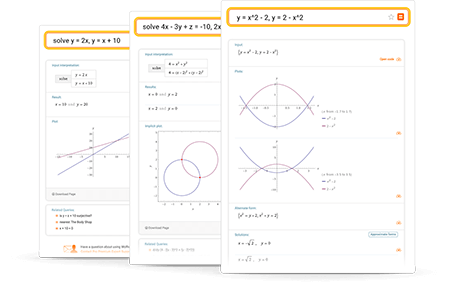
Wolfram|Alpha is capable of solving a wide variety of systems of equations. It can solve systems of linear equations or systems involving nonlinear equations, and it can search specifically for integer solutions or solutions over another domain. Additionally, it can solve systems involving inequalities and more general constraints.

Learn more about:

Видео:Шиз поясняет. Wolfram MathematicaСкачать

Tips for entering queries

Enter your queries using plain English. To avoid ambiguous queries, make sure to use parentheses where necessary. Here are some examples illustrating how to ask about solving systems of equations.

Видео:ТОП приложение для СТУДЕНТОВ в изучении математики! ChatGPT больше не нужен? Эта программа решит всеСкачать

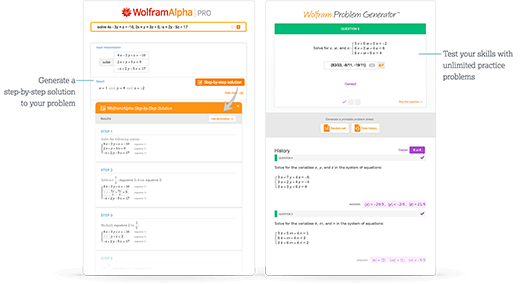
Access instant learning tools

Get immediate feedback and guidance with step-by-step solutions and Wolfram Problem Generator

Learn more about:

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

What are systems of equations?

A system of equations is a set of one or more equations involving a number of variables.

The solutions to systems of equations are the variable mappings such that all component equations are satisfied—in other words, the locations at which all of these equations intersect. To solve a system is to find all such common solutions or points of intersection.

Systems of linear equations are a common and applicable subset of systems of equations. In the case of two variables, these systems can be thought of as lines drawn in two-dimensional space. If all lines converge to a common point, the system is said to be consistent and has a solution at this point of intersection. The system is said to be inconsistent otherwise, having no solutions. Systems of linear equations involving more than two variables work similarly, having either one solution, no solutions or infinite solutions (the latter in the case that all component equations are equivalent).

More general systems involving nonlinear functions are possible as well. These possess more complicated solution sets involving one, zero, infinite or any number of solutions, but work similarly to linear systems in that their solutions are the points satisfying all equations involved. Going further, more general systems of constraints are possible, such as ones that involve inequalities or have requirements that certain variables be integers.

Solving systems of equations is a very general and important idea, and one that is fundamental in many areas of mathematics, engineering and science.

Видео:КиЯ 0.18 | Решение уравнения и отображение его корней в Wolfram LanguageСкачать

Алгебра

Можно проводить факторизацию или раскрывать алгебраические выражения:

(Используйте CTRL + 6 для ввода степени.)

Out[1]=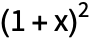

Wolfram mathematica решить систему уравнений

В Языке Wolfram символ == (два знака равенства) используется для проверки равенства:

Out[1]=

Объединим алгебраические выражения с помощью == для формирования уравнения:

Out[2]=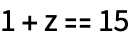

Функции, такие как Solve позволяют найти точные решения уравнений:

Out[1]=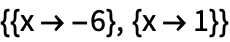

Для приближенных результатов используйте NSolve:

Out[2]=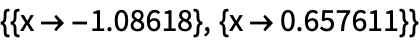

Систему уравнений можно передать функции в виде списка:

Out[3]=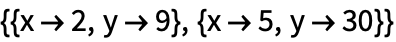

Найдем корни уравнения:

Out[1]=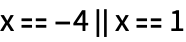

В случае если полином не так просто разложить на множители, то лучше использовать приближенные решения:

Out[2]=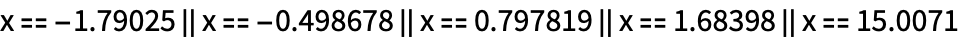

Функция Reduce сводит системы неравенств к простой форме:

Out[1]=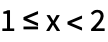

Упрощенная форма может состоять из нескольких интервалов:

Out[2]=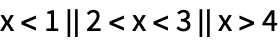

Функция NumberLinePlot — это удобный способ визуализации этих результатов:

Out[3]=

Большое число уравнений и формул доступно через естественную форму ввода:

Видео:Решение системы уравнений методом ГауссаСкачать

7. Уравнения и системы уравнений

Уравнения и системы уравнений

Многие математические задачи сводятся к решению в общем случае нелинейных уравнений вида f(x) = 0 или f(x) = expr.

В системе Mathematica они обозначаются как eqns (от слова equations — уравнения). Разумеется, могут решаться и системы, состоящие из ряда таких уравнений.

Для решения уравнений (как одиночных, так и систем) в численном и символьном виде Mathematica имеет функцию Solve:

Solve [eqns, vars] — предпринимает попытку решить уравнение или систему уравнений eqns относительно переменных vars;
Solve [eqns, vars, elims] — пытается решать уравнения eqns по переменным vars, исключая переменные elims.

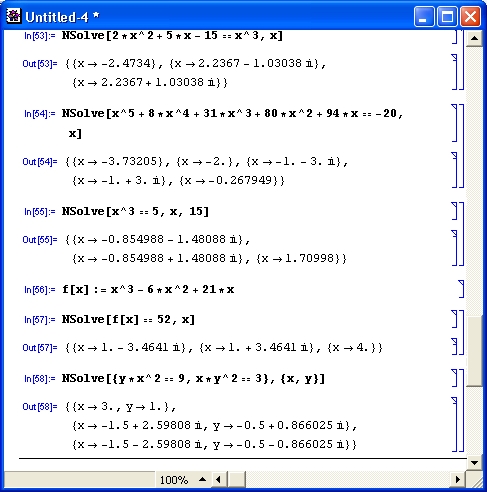
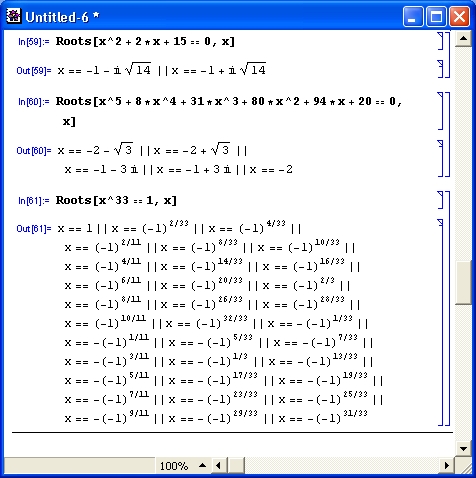
Входные параметры этой функции могут быть представлены списками или записаны выражениями через объединительный знак«&&». В eqns в качестве знака равенства используется знак «= =». Примеры применения функции Solve представлены на рис. 4.12.

Рис. 4.12. Примеры решения уравнений

Обратите внимание на то, что в определенных ситуациях система подсказывает тонкости решения, выдавая предупреждающие сообщения. Если такие ситуации не являются ошибками, препятствующими решению, то полученное решение выводится в ячейку вывода.

Решение систем нелинейных уравнений в символьном виде

Приведенные на рис. 4.13 примеры показывают решение систем нелинейных уравнений с помощью функции Solve.

Достаточно характерен пример с применением функции N. Если убрать в нем функцию N, то будет получен чрезвычайно громоздкий, хотя и точный результат (проверьте это сами, поскольку размеры результата делают нецелесообразным его приведение в книге). Функция N осуществляет выполнение всех промежуточных вычислений, благодаря чему результат получается вполне обозримым и представленным в комплексных числах.

В последнем примере рис. 4.13 получен набор из пяти пар корней, определенных через функцию Root. Эта функция, в свою очередь, означает вычисление корней полиномиального уравнения пятой степени. Данный пример, как и ранее приводимые решения кубического уравнения, является наглядной иллюстрацией того, что простота нелинейных уравнений порой оказывается весьма обманчивой, а их решение порой приводит к весьма громоздким и сложным результатам. Тем не менее, возможность решения отдельных нелинейных уравнений и их систем в символьном виде трудно переоценить. К сожалению, далеко не все уравнения имеют такие решения — многие можно решать только в численном виде.

Рис. 4.13. Примеры решения систем нелинейных уравнений

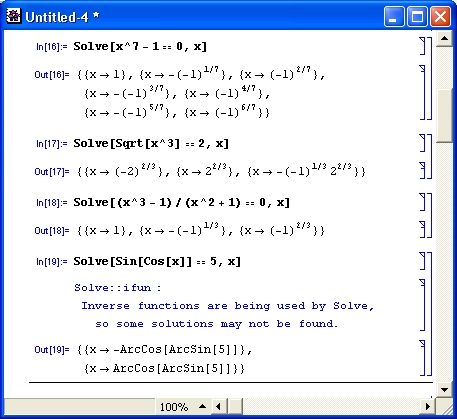
Не следует полагать, что Mathematica всегда выдает верное решение систем нелинейных уравнений. На самом деле решение иногда бывает ошибочным. Поэтому в большинстве случаев стоит оформлять решение таким образом, чтобы обеспечить его проверку. Для этого рекомендуется отдельно задать систему уравнений и результат решения. Тогда проверка легко осуществляется с помощью подстановки. Два примера решения систем уравнений с проверкой решений показаны на рис. 4.14.

В первом примере решение кажется очевидным (равенства выполняются, например, при х=2 и у=3). Однако здесь Mathematica дает сразу три пары решений, и все они оказываются верны, поскольку после подстановки проверка всех равенств возвращает True.

А вот во втором примере проверка дала не совсем обычный результат, что связано с наличием в решении неопределенной переменной а. В таких случаях стоит попробовать упростить решение с помощью функции Simplify, что и показано на рис. 4.14.

Рис. 4.14. Примеры решения уравнений с проверкой

Опции функции Solve

С функцией Solve можно использовать ряд опций. Их можно вывести командой Options [Solve]. Ниже описано их назначение:

InverseFunctions — указывает, следует ли использовать обратные функции;
MakeRules — указывает, должен ли результат быть представлен как объект AlgebraicRulesData;
Method — устанавливает алгоритм, используемый для вычисления результата (возможны методы 1, 2 и 3);
Mode — задает характер решения уравнения (возможны Generic, Modular и Rational);
Sort — устанавливает, нужна ли сортировка результатов;
Verif ySolutions — устанавливает, следует ли проводить проверку полученных решений и удаление посторонних решений;
WorkingPrecision — устанавливает число цифр промежуточных вычислений (по умолчанию Infinity).

На рис. 4.15 приведены примеры применения функции Solve с опцией Inverse-Functions.

Обратите внимание на то, что последняя система уравнений при отсутствии опции InverseFunctions решается с предупреждением. Она вообще не решается, если эта опция задана как False, и гладко решается при InverseFunctions -> True.

Рис. 4.15. Примеры решения уравнений с опцией InverseFunction

То, насколько может влиять на решение опция Method, наглядно показывают примеры, представленные на рис. 4.16.

Рис. 4.16. Примеры решения уравнений разными методами

Множество примеров решения систем нелинейных уравнений в символьном виде можно найти в справочной системе Mathematica.

Численное решение уравнений

Многие нелинейные уравнения и системы нелинейных уравнений в принципе не имеют аналитических решений. Однако их решение вполне возможно численными методами. Для численного решения систем нелинейных уравнений используется функция NSolve:

NSolve [eqns, vars] — пытается численно решить одно уравнение или систему уравнений eqns относительно переменных vars;
NSolve [eqns, vars, elims] — пытается численно решить уравнения eqns относительно vars, исключая переменные elims.

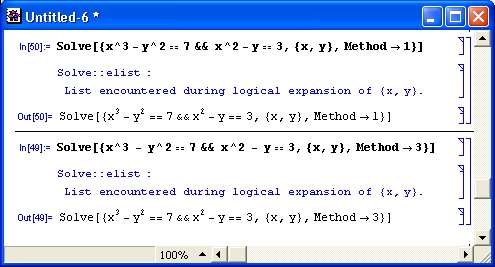
С этой функцией используется единственная опция WorkingPrecision, задающая число верных цифр результата — по умолчанию 16. На рис. 4.17 представлены примеры использования функции NSolve для численного решения уравнений.

Риc. 4.17. Примеры численного решения уравнений

Результаты решения с помощью функции NSolve также рекомендуется проверять с помощью подстановки, например, так:

Нетрудно заметить, что в данном случае решение верно.

Поиск корней уравнений

Для вычисления корней полиномиальных уравнений используется функция Roots:

На рис. 4.18 представлены примеры применения функции Roots.

Рис. 4.18. Примеры использования функции Roots

Формат выдачи результатов для функции Roots отличается от такового для функции Solve. Поэтому проверку решения подстановкой надо выполнять как в следующем примере:

х == -3.56155 | | х == 0.561553

Для преобразования результата вычислений в список решений (подобный решениям, получаемым с помощью функции Solve) здесь использована функция ToRules.

При затруднениях в решении уравнений с помощью функции Roots можно использовать следующие опции:

True, Eliminate -> False, EquatedTo-> Null,

Modulus -> 0, Multiplicity->1, Quar tics -> True, Using -> True>

Ниже они описаны подробно:

Cubics — указывает, следует ли искать явные решения для неприводимых кубических уравнений;
EquatedTo — задает выражение для замещения переменной в решении;
Modulus — задает промежуточную факторизацию полинома;
Multiplicity— устанавливает кратность каждого из корней в конечном результате;
Quartics — задает точное решение квадратного уравнения и полинома четвертой степени;
Using — указывает какие-либо дополнительные уравнения, которые следует использовать для решения уравнений.

Применение опций нередко позволяет получать решения, которые не удаются с первого раза. Однако это требует определенного опыта и понимания сути решаемой задачи.

Дополнительные функции для решения уравнений

Имеется также ряд дополнительных функций, которые используются описанными ранее функциями и также могут применяться при решении нелинейных уравнений:

Auxiliary [v] — применяется модулем Solve для указания того, что переменная v должна использоваться функцией Roots для результирующих решений, но соответствующие значения v не должны быть включены в окончательный ответ;
Eliminate [eqns, vars] — исключает переменные vars из системы уравнений eqns;
FindRoot [Ihs == rhs, ] — ищет численное решение уравнения Ihs == rhs, начиная с х = x0;
MainSolve [eqns] — основная функция для преобразования системы уравнений. Ее вызывают Solve и Eliminate. Уравнения должны быть представлены в форме Ihs == rhs. Они могут объединяться с помощью && и | |. MainSolve возвращает False, если не существует решения уравнений, и возвращает True, если все значения переменных являются решениями. MainSolve перестраивает уравнения, применяя определенные директивы;
MainSolve [eqns, vars, elim, rest] — пытается перестраивать уравнения eqns так, чтобы найти решения для переменных vars и исключить переменные elim. Список rest может включаться для указания порядка исключения любых остальных переменных;
NRoots [lhs==rhs, var] — возвращает список численных приближений корней полиномиального уравнения;
Residue [ехрr, ] — ищет вычет ехрг в точке х = х0;
SolveAlways [eqns, vars] — возвращает значения параметров, которые превращают уравнения eqns в тождества для всех значений переменных vars.

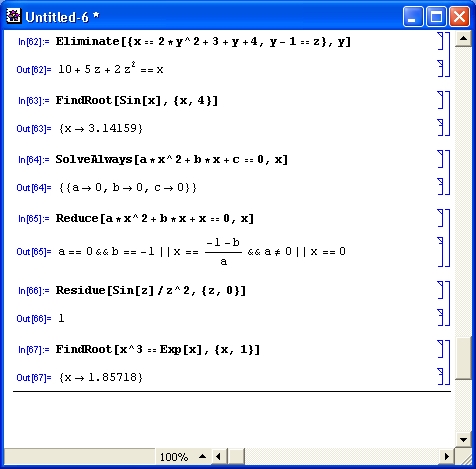
Примеры использования некоторых из этих функций показаны на рис. 4.19.

Рис. 4.19. Примеры применения дополнительных функций для решения уравнений

В целом надо отметить, что система Mathematica обладает обширными средствами для решения уравнений и их систем. Умение их применять — залог правильного и эффективного решения сложных математических задач, относящихся к классу решения уравнений.

Графическая иллюстрация и выбор метода решения уравнений

При рассмотрении приведенных выше примеров может сложиться благодушное впечатление о том, что решение нелинейных уравнений может производиться автоматически и без размышлений. Но это далеко не так — представленные выше примеры просто подобраны так, что они имеют решение с помощью соответствующих функций.

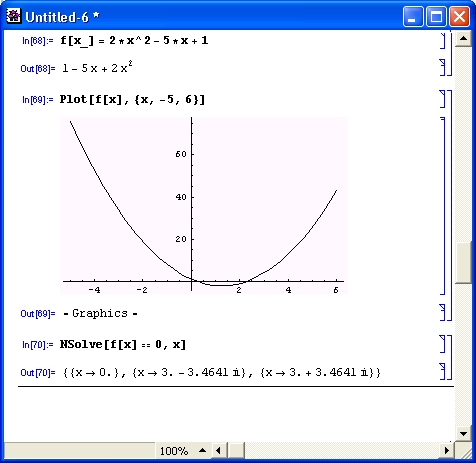
На самом деле порой даже простые уравнения могут не иметь решения. В сложных случаях очень полезна графическая визуализация решения. В качестве примера на рис. 4.20 показана визуализация вычисления корней квадратного уравнения. В данном случае график функции явно указывает на существование двух действительных корней при х, близких к 0.2 и 2.3. Функция Nsolve без труда находит оба корня.

Рис. 4.20. Визуализация решения квадратного уравнения для случая двух действительных корней

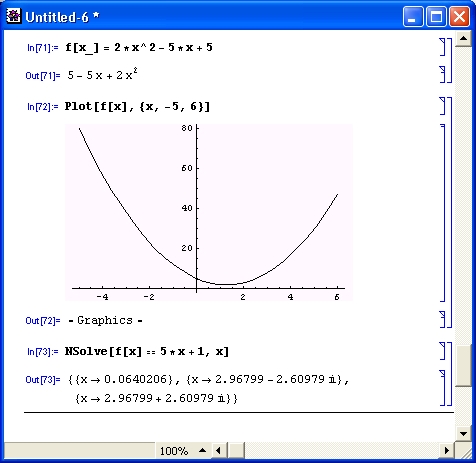
А вот на рис. 4.21 показан случай, когда из-за изменения последнего члена квадратичной функции ее график уже не пересекает ось х вообще. Это говорит о том, что решения в виде действительных корней нет. И в самом деле, NSolve находит корни как комплексно-сопряженные числа. Действительная часть найденных корней дает координату х для впадины кривой — параболы.

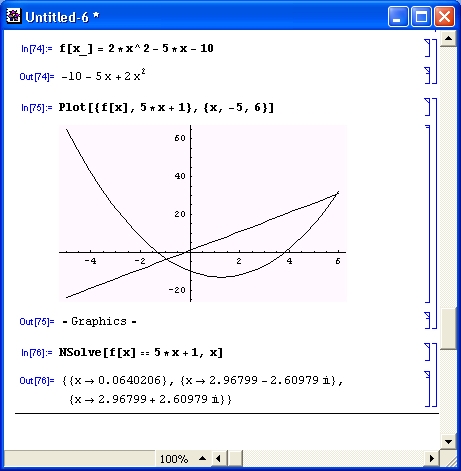
Если требуется решение равенства f1(х) = f ₂ (x), то для графической визуализации решения можно построить графики функций f1(х) и f ₂ (лг) — наличие точек их пересечения будет означать существование действительных корней. Этот случай иллюстрирует рис. 4.22. В данном случае проблем с решением нет, поскольку, по существу, решается квадратное уравнение.

Рис. 4.21. Визуализация решения квадратного уравнения для случая двух комплексных корней

Рис. 4.22. Пример визуализации решения уравнения вида f(x) = 5х + 1

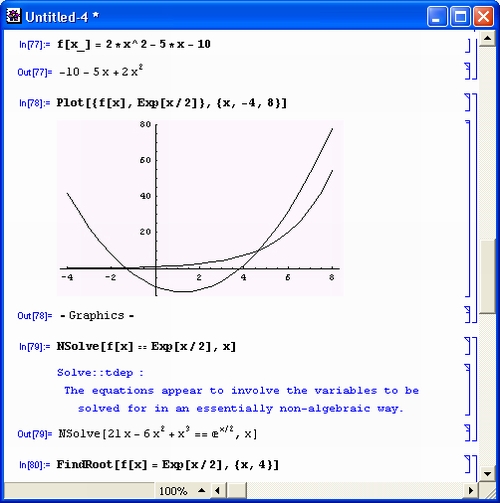
Но вот на рис. 4.23 показан случай решения уравнения f(x) = ехр(х/2). Графики функций ясно показывают, что парабола пересекается экспонентой в двух точках. Однако функция NSolve отказывается решать такое уравнение и выдает сообщение о том, что оно является трансцендентным.

Таким образом, в данном случае наличие графического решения говорит о необходимости смены функции, с помощью которой до сих пор решались уравнения. Подходящей в данном случае является функция FindRoot, которая отыскивает одно решение вблизи заданной начальной точки. Применив ее дважды, нетрудно получить оба корня данного уравнения.

Рис. 4.23. Пример решения уравнения вида f(x) = ехр(х/2)

Приведенные примеры далеко не исчерпывают проблему графической визуализации решения и выбора методов решения. Однако они иллюстрируют возможности системы Mathematica в этой области и заостряют внимание на потенциальных проблемах. Для реализации численных расчетов в системе Mathematica отобраны наилучшие и наиболее эффективные численные методы из описанных в литературе, в том числе в отечественной.

Получение сразу нескольких корней

Многие уравнения с тригонометрическими функциями могут иметь периодические или близкие к ним решения. К сожалению, функции Mathematica, вычисляющие корни уравнений, не способны в этом случае дать сразу несколько корней. Однако ситуация тут далеко не безнадежна — приведенный ниже пример наглядно показывает это.

Пусть требуется в интервале изменения х от 0 до 20 найти все решения уравнения

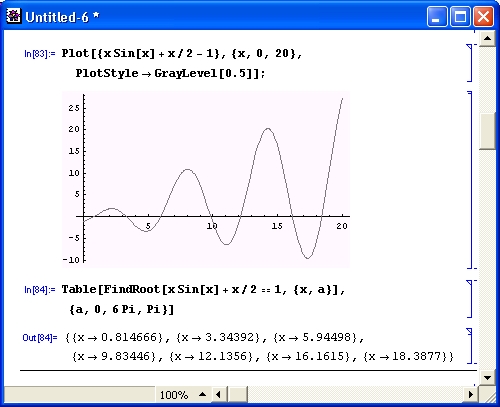
График функции, представляющей левую часть уравнения, показан на рис. 4.24. Хорошо видно, что он пересекает ось х семь раз, то есть имеет в интересующем нас диапазоне семь корней.

Рис. 4.24. График функции х sin(x) + х/2 — 1 и пример вычисления всех ее корней в интервале изменения х от 0 до 20

Колебательная составляющая функции обусловлена входящей в нее функцией sin(x), которая имеет нули в точках 0, n, 2n, Зn. Однако, как видно из рис. 4.24, эти значения лишь приближенные, ввиду влияния других членов уравнения.

Ключевая идея получения всех корней уравнения заключается в поиске нужных решений с помощью функции FindRoot, которой последовательно подставляются различные начальные приближения. Однако вместо уже испытанного приема — поиска корней поодиночке — можно воспользоваться «таблицей» решений, используя функцию Table. Решение, приведенное под графиком функции на рис. 4.24, наглядно иллюстрирует возможности этого приема — найдены (или, вернее, уточнены) все семь корней исходного уравнения.

Получение неизвестных в явном виде

Читатель, возможно, обратил внимание на то, что решения всех представленных выше примеров выглядят не совсем обычно — в виде списка подстановок. Это не позволяет использовать неизвестные в явном виде, например, для проверки решений или передачи найденных неизвестных в последующие вычислительные блоки. Однако от этого затруднения легко избавиться, если перед конструкций блока решения использовать выражение следующего вида:

Список переменных в этом выражении должен однозначно соответствовать списку неизвестных системы уравнений. Покажем этот прием в действии. Ниже приведено решение системы из трех нелинейных уравнений:

Обратите внимание на то, что вывод списка не дает полученных значений неизвестных. Это связано с тем, что переменные в блоке решения имеют ло-к(1лъный характер и за пределами блока их значения (в том числе неопределенные) сохранятся такими, какими они были до применения в блоке решения.

Теперь зададим решение в ином виде:

Как видите, на сей раз решение получено в виде списка с числами — явными значениями неизвестных. Можно обозначить их как а, Ь и с, получить список и даже использовать их отдельно:

Теперь можно проверить решение данной системы:

Полученный вектор правых частей системы совпадает с заданным, что свидетельствует о правильности решения. Разумеется, вместо нового списка для вектора решения можно было использовать и вектор .