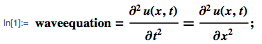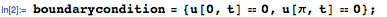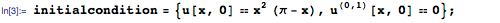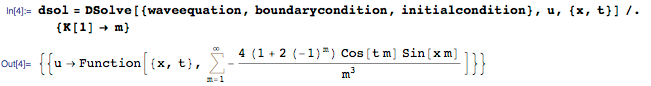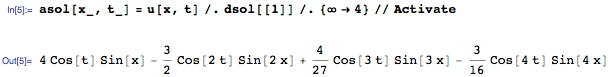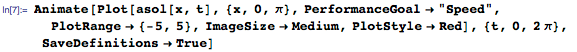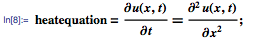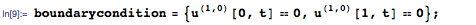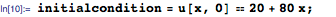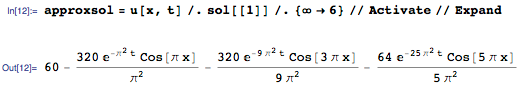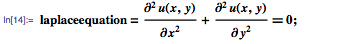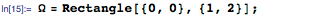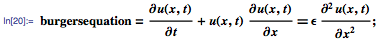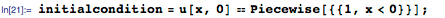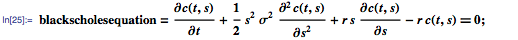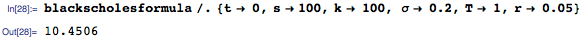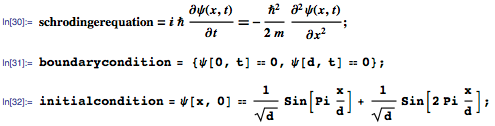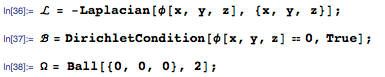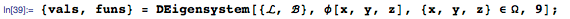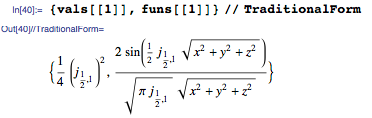Wolfram mathematica численное решение дифференциальных уравнений (2 видео)

Содержание

Wolfram mathematica численное решение дифференциальных уравнений
WolframAlpha по-русски
Численное решение обыкновенных дифференциальных уравнений в Wolfram|Alpha
Как решать дифференциальные уравнения в wolfram mathematica
WolframAlpha по-русски
Решение обыкновенных дифференциальных уравнений в Wolfram|Alpha
Новое в Wolfram Language | Аналитическое решение уравнений в частных производных
Иллюстрированный самоучитель по Mathematica 3/4
Дифференциальные уравнения. Решение дифференциальных уравнений в символьном виде.
📺 Видео

Видео:Численное решение задачи Коши методом ЭйлераСкачать

Wolfram mathematica численное решение дифференциальных уравнений

Решение дифференциальных уравнений в символьном виде

Дифференциальными принято называть уравнения, в состав которых входят производные функции у(х), представляющей решение уравнения. Дифференциальные уравнения могут быть представлены в различной форме, например в общеизвестной форме Коши:

Несколько дифференциальных уравнений образуют систему дифференциальных уравнений. Решение таких систем также возможно средствами Mathematica и подробно описано в ряде книг по использованию системы 71. Дифференциальные уравнения и системы дифференциальных уравнений могут быть линейными и нелинейными. Для линейных уравнений обычно существуют решения в аналитическом виде. Нелинейные дифференциальные уравнения в общем случае аналитических решений не имеют, но могут решаться приближенными численными методами.

Дифференциальные уравнения широко используются в практике математических вычислений. Они являются основой при решении задач моделирования — особенно в динамике. Немногие математические системы имеют реализации численных методов решения систем дифференциальных уравнений. Но система Mathematica имеет средства как для символьного, так и для численного решения дифференциальных уравнений и их систем.

Для решения дифференциальных уравнений в символьном виде используются следующие средства:

DSolve[eqn, y[x], х] — решает дифференциальное уравнение относительно функций у [ х ] с независимой переменной х;
DSolve[, , ]-решает систему дифференциальных уравнений.

У функции DSolve и ее численного варианта NDSolve есть пара опций, на которые следует обратить внимание:

DSolveConstants — опция к DSolve, определяющая постоянные интегрирования, которые будут использованы в результате;
StartingStepSize — опция к NDSolve, определяющая величину начального шага.

В решении дифференциальных уравнений встречаются постоянные интегрирования. По умолчанию они обозначаются как С [ i ].

Приведем примеры решения дифференциальных уравнений:

DSolve [у» [х] — у’ [х] — 6 у [х] == 0, у [х] , х] <| е-4хС[1] + С[2] -Cos[2x] -|sin[2x]>>

DSolve [у» [х] + 4 у'[х] == 10 Sin [2 х] , у [х] , х]

DSolve[y'[x] == Sin[Ex] , y[x] , x]

DSolvefz2 w»[z] +zw'[z] — (z2 + l)w[z] ==0, w[z], z]

Как нетрудно заметить, аналитические решения дифференциальных уравнений могут содержать не только элементарные, но и специальные математические функции, что заметно расширяет возможности применения системы Mathematica в решении задач динамического моделирования.

Решение дифференциальных уравнений в численном виде

Многие дифференциальные уравнения не имеют аналитических решений — например, нелинейные. Однако они могут с приемлемой точностью решаться численными методами. Для численного решения систем дифференциальных уравнений используется функция NDSolve:

NDSolve [eqns, у, ]— ищет численное решение дифференциальных уравнений .eqns относительно функции у независимой переменной х в интервале от xmin до xmax;
NDSolve [eqns, , ]— ищет численные решения относительно функций yi.

MaxSteps — опция к NDSolve, которая определяет максимальное количество шагов.

Часто весьма желательно выводить результаты решения дифференциальных уравнений в графической форме. Рисунок 4.25 поясняет, как это делается при решении системы нелинейных дифференциальных уравнений, описывающих достаточно сложный колебательный процесс.

Нередко решение предпочитают представить на фазовой плоскости. Рисунок 4.26 иллюстрирует такую возможность. Более того, поскольку решается система из трех дифференциальных уравнений, фазовая траектория решения находится в трехмерном пространстве.

Простота задания решения и вывода его результатов в графической форме открывает широкие возможности применения системы для математического моделирования сложных явлений. При этом, в отличие от такого решения с помощью обычных языков высокого уровня (например, Фортран, Бейсик, Паскаль или С), не требуется составления каких-либо программ по реализации численных методов решения систем дифференциальных уравнений, таких как, скажем, метод Рунге— Кутта. Они представлены в виде уже готовых функций.

Рис. 4.25. Решение системы дифференциальных уравнений с выводом решения в виде графиков временных зависимостей

Рис. 4.26. Решение системы дифференциальных уравнений с выводом решения в форме кривых на фазовых плоскостях

Видео:КиЯ 0.18 | Решение уравнения и отображение его корней в Wolfram LanguageСкачать

WolframAlpha по-русски

Математика с WolframAlpha ® . Объяснения с примерами.

Численное решение обыкновенных дифференциальных уравнений в Wolfram|Alpha

solve (метод интегрирования) [шаг интегрирования] [отрезок интегрирования]

Обязательные параметры — само дифференциальное уравнение, начальные условия и численный метод интегрирования.

Не забудьте, что количество начальных условий должно совпадать с порядком уравнения. Иначе, Wolfram Alpha автоматически подставит в запрос свои начальные или краевые условия.

Рекомендуется указывать явно отрезок интегрирования. Без этого Wolfram Alpha автоматически выполнит 10 шагов интегрирования по умолчанию. Можно явно указать шаг интегрирования. В противном случае, Wolfram Alpha установит шаг интегрирования по умолчанию, как в следующем примере:

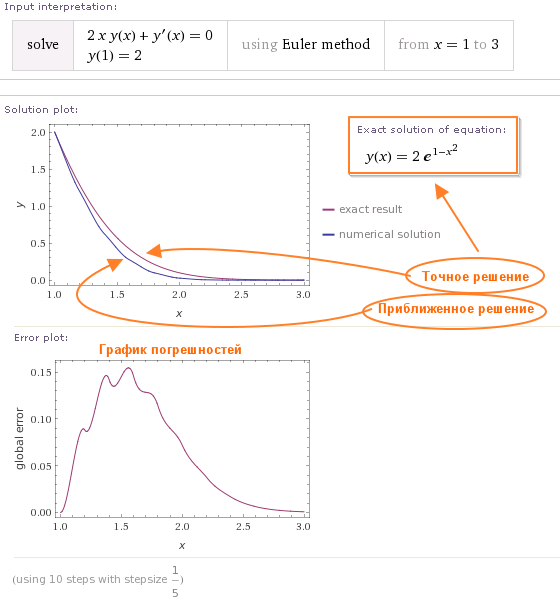
Когда дифференциальное уравнение, которое вы решаете численным методом, допускает также аналитическое решение, тогда по запросу solve система Wolfram Alpha выводит точную и приближенную интегральные кривые уравнения, соответствующие заданным начальным условиям, а также график погрешностей, таблицу значений искомой функции, таблицу погрешностей, и, конечно, само аналитическое решение:

Кроме того, здесь Wolfram Alpha выводит таблицу для сравнения погрешностей всех численных методов, которые использует система (в крайней точке интервала интегрирования дифференциального уравнения):

В рассмотренном примере шаг интегрирования, равный 0.2, был выбран автоматически. Выше было сказано, что можно явно указать нужный шаг интегрирования. Причем, нужно выбирать его так, чтобы на заданном отрезке умещалось не менее, чем 10 шагов интегрирования. Уменьшая шаг интегрирования, можно получать численные решения с желаемой точностью точностью:

Численные решения дифференциальных уравнений, рассмотренные выше, были получены простейшим методом — методом Эйлера (Euler method). Как мы видели выше, Wolfram Alpha реализует и другие численные методы интегрирования дифференциальных уравнений. Посмотрите примеры (по ссылке):

Euler method — метод Эйлера;
midpoint method — метод средних точек, модифицированный метод Эйлера;
Heun’s method (метод Хойна, вариант модифицированного метода Эйлера)
third‐order Runge‐Kutta method (метод Рунге-Кутты третьего порядка)
fourth‐order Runge‐Kutta method (метод Рунге-Кутты четвертого порядка)
Runge‐Kutta‐Fehlberg method (метод Рунге-Кутты-Фелберга, RKF method )
Bogacki‐Shampine method
Dormand‐Prince method (DOPRI method)
backward Euler method
implicit midpoint method

С помощью Wolfram Alpha, можно решать не только обыкновенные дифференциальные уравнения 1-го порядка (ОДУ-1), но и обыкновенные дифференциальные уравнения высших порядков. Например, вот так Wolfram Alpha решает обыкновенное дифференциальное уравнение 3-го порядка:

Таким образом, численное решение обыкновенных дифференциальных уравнений в системе Wolfram Alpha является достаточно простой стандартной процедурой, соблюдение которой гарантирует правильный результат.

Видео:12.01 Решение систем ДУ в Wolfram MathematicaСкачать

Как решать дифференциальные уравнения в wolfram mathematica

Видео:Метод ЭйлераСкачать

WolframAlpha по-русски

Математика с WolframAlpha ® . Объяснения с примерами.

Решение обыкновенных дифференциальных уравнений в Wolfram|Alpha

Решение дифференциальных уравнений с выводом результатов в пошаговом представлении (функция «Show steps» — Показать шаги) является одной из важных особенностей Wolfram|Alpha.

Wolfram|Alpha в большинстве случаев может помочь в решении дифференциальных уравнений различного уровня сложности, начиная от простейших дифференциальных уравнений первого порядка с разделяющимися переменными (separable equations ) и включая более сложные уравнения, для решения которых служат, например, методы операционного исчисления, использующие преобразование Лапласа.

Как видим, Wolfram|Alpha сначала определяет (классифицирует) этот пример, как обыкновенное линейное дифференциальное уравнение первого порядка, затем выводит общее решение данного уравнения, график частного решения, удовлетворяющего условию y(1)=1, а также семейство интегральных кривых данного уравнения.

Чтобы получить детальное пошаговое решение, используйте кнопку «Show steps»:

Видео:Численное решение системы дифференциальных уравнений(задачи Коши)Скачать

Новое в Wolfram Language | Аналитическое решение уравнений в частных производных

Перевод поста Devendra Kapadia «New in the Wolfram Language: Symbolic PDEs».
Код, приведенный в статье, можно скачать здесь.
Выражаю огромную благодарность Кириллу Гузенко KirillGuzenko за помощь в переводе и подготовке публикации. Уравнения в частных производных (УрЧП) играют очень важную роль в математике и ее приложениях. Их можно использовать для моделирования реальных явлений, таких как колебания натянутой струны, распространения потока тепла в стержне, в финансовых областях. Цель этой статьи — приоткрыть завесу в мир УрЧП (тем кто еще с ним не знаком) и ознакомить читателя с тем, как можно эффективно решать УрЧП в Wolfram Language, используя новый функционал для решения краевых задач в DSolve, а так же новую функцию DEigensystem, которая появилась в версии 10.3.

История УрЧП восходит к работам известных математиков восемнадцатого века — Эйлера, Даламбера, Лапласа, однако развитие этой области в последние три столетия так и не остановилось. И потому в статье я приведу как классические, так и современные примеры УрЧП, что позволит рассмотреть эту область знаний под разными углами.

Давайте начнем с рассмотрения колебаний натянутой струны с длиной π, закрепленной на обоих концах. Колебания струны можно смоделировать с помощью одномерного волнового уравнения, приведённого ниже. Здесь u(x,t) — вертикальное смещение точки струны с координатой х в момент времени t:

Затем мы задаём граничные условия, указав тем самым, что концы струны при колебаниях сохраняют свои положения.

Зададим теперь начальные условия для движения струны, указав смещения и скорости различных точек струны в момент времени t=0:

Теперь мы можем использовать DSolve для решения волнового уравнения с начальными и краевыми условиями:

Как указано выше, решение есть бесконечная сумма тригонометрических функций. Сумма возвращается в невычисленной форме (Inactive), поскольку каждый отдельный член разложения имеет физическую интерпретацию, и зачастую даже небольшое количество членов может являться хорошим приближением. К примеру, мы можем взять первые четыре члена для получения приближенного решения asol(x,t)

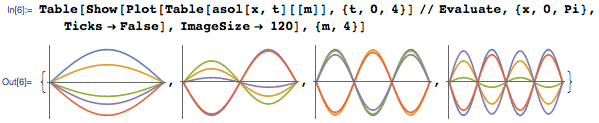
Каждый член в сумме представляет собой стоячую волну, которые могут быть представлены следующим образом:

И все эти стоячие волны складываются воедино, образуя гладкую кривую, как показано на анимации ниже:

Волновое уравнение относится к классу линейных гиперболических уравнений в частных производных, описывающих распространение сигналов с конечными скоростями. Это УрЧП представляет собой удобный способ для моделирования колебаний в струне или в каком-то другом деформирумом теле, однако ещё более важную роль оно играет в современной физике и инженерных приложениях, т.к. оно описывает распространение света и электромагнитных волн.

Давайте теперь смоделируем поток тепла в стержне единичной длины, изолированном с обоих концов, с помощью представленного ниже уравнения теплопроводности:

Поскольку стержень изолирован с обоих концов, то через них проходит нулевой поток тепла, что можно выразить как граничные условия вида х = 0 и х = 1:

Теперь нужно указать начальное температурное распределение в стержне. В этом примере мы будем использовать приведённую ниже линейную функцию. В левом конце (х = 0) начальная температура — 20 градусов, в правом (х = 1) — 100:

И теперь мы можем решить уравнение теплопроводности с заданными условиями:

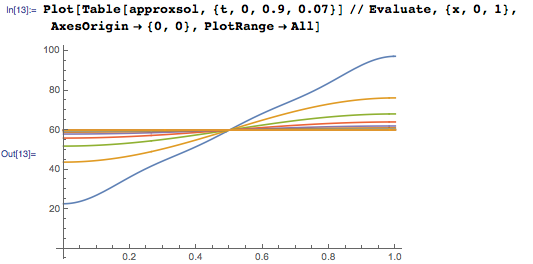
Как и в приведённом выше примере с волновым уравнением, мы можем извлечь несколько членов суммы и получить приближенное решение:

Первый член приближенного решения — 60 — среднее от температур на границах стержня, и она является стационарной температурой для этого стержня. Как показано на графике функции температуры от длины, представленном ниже, температура стержня быстро достигает стационарного значения в 60 градусов:

Уравнение теплопроводности относится к классу линейных параболических уравнений в частных производных, которые описывают процессы диффузии. Это простое на вид уравнение часто можно встретить в самых различных, а иногда и весьма неожиданных областях. Далее в статье мы рассмотрим два примера этого явления.

Рассмотрим теперь уравнение Лапласа, которое используется для моделирования стационарного состояния систем, т. е. поведения после некоторых зависящих от времени уже законченных переходных процессов. В двумерном случае это уравнение можно представить следующим образом:

Ограничим координаты х и у прямоугольной областью Ω, как показано ниже:

Классическая задача Дирихле — найти функцию u(x,y), удовлетворяющую уравнению Лапласа внутри области Ω с заданным условием Дирихле (DirichletCondition), которое определяет значения на границах области Ω, как показано ниже:

Задачу Дирихле можно решить с помощью функции DSolve, весьма изящно задав при этом область:

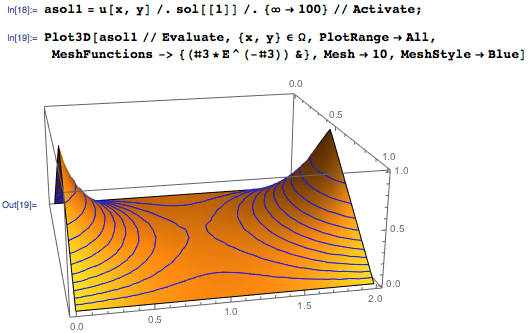
Как и в примерах ранее, мы можем извлечь некоторое количество членов (скажем, 100) из суммы и визуализировать решение:

Следует заметить, что решение u(x,y) задачи Дирихле представляется гладким в Ω, несмотря на то, что граничные условия имеют резкие черты. Помимо этого, u(x,y) достигает экстремальных значений на границах, в то время как в центре прямоугольника находится седловая точка. Эти черты характерны для линейных эллиптических уравнений — класса уравнений в частных производных, к которым и принадлежит уравнение Лапласа.

Волновое уравнение, уравнение теплопроводности, уравнение Лапласа — самые известные примеры классических УрЧП. Теперь мы рассмотрим три примера типичных современных УрЧП, первым среди которых будет уравнение Бюргерса для вязкой жидкости, которое может быть представлено следующим образом:

Это нелинейное УрЧП было введено Иоханнесом Бюргерсом в сороковых годах в качестве простой модели для турбулентных потоков (параметр ϵ в уравнении представляет собой вязкость жидкости). Однако, десять лет спустя, Э. Хопф и Д. Коул показали, что уравнение Бюргерса сводится к уравнению теплопроводности, а это значит, что данное уравнение не может проявлять хаотического поведения. Преобразование Коула-Хопфа позволяет решать уравнения Бюргерса в замкнутой форме для начального условия, заданного, к примеру, так:

В этом примере мы будем использовать функцию DSolveValue, которая возвращает только выражение для решения. Члены с функцией ошибок (Erf) в формуле ниже возникают из решения соответствующей граничной задачи теплового уравнения:

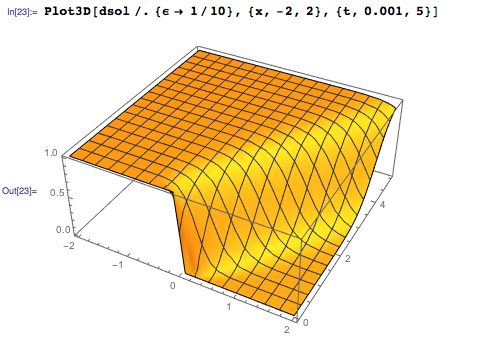
Представленный ниже график демонстрирует изменение во времени гипотетического одномерного поля скоростей потока. Решение представляется гладким для положительного ϵ, при том что начальное условие есть кусочно заданная функция:

Как можно заметить на нижепреведённых графиках, решение стремится к разрывному при сремлении вязкости ϵ к нулю. Подобные решения с резким переходом (shock solutions) — известная особенность уравнений Бюргерса для невязкой (ϵ = 0) среды.

В качестве второго примера современных УрЧП рассмотрим уравнение Блэка-Шоулза, используемое в финансовых расчётах. Это уравнение впервые представили Фишер Блэк и Майрон Шоулз в 1973 году в качестве модели для определения теоретической цены на европейские опционы, и формулируется оно следующим образом:

где:
c — цена опциона как функция от стоимости акций s и времени t,
r — процентная ставка без риска,
σ — волатильность акций.

В их эпохальной статье (которая была процитирована более 28000 раз), Блэк и Шоулз отметили, что их уравнения с помощью преобразования переменных могут быть сведены к уравнению теплопроводности. Это резкое упрощение приводит к знаменитой формуле Блэка-Шоулза для европейских опционов с конечными условиями, основанными на цене исполнения (strike price) k актива в момент времени t=Т:

Вооружившись этой формулой, мы можем вычислить значения финансовых опционов для типичных значений параметров:

Ответ согласуется со значением, полученным с помощью встроенной функции FinancialDerivative:

В качестве третьего примера современных УрЧП рассмотрим уравнение Шредингера для электрона в одномерной потенциальной яме с глубиной d и соответствующим начальным условием. Уравнение и условия можно сформулировать следующим образом:

Этот пример имеет элементарное решение, которое принимает мнимые значения из-за наличия I в уравнении Шредингера:

Функция плотности вероятности для электрона ρ = Ψ ⊹ Ψ, с использованием подходящих значений параметров в задаче, может быть вычислена следующим образом:

Мы можем создать анимацию изменения плотности вероятности во времени, которая показывает, что «центр» электрона в яме движется из стороны в сторону:

Собственные значения и собственные функции играют важную роль как в решении уравнения Шрёдингера, так и в других УрЧП. В частности, они предоставляют «строительные блоки» для решений волновых уравнений и уравнений теплопроводности в виде бесконечных сумм, которые приводились ранее в статье. Поэтому, в качестве нашего последнего примера рассмотрим задачу о нахождении девяти наименьших собственных значений и собственных функций для оператора Лапласа с однородным (нулевым) условием Дирихле для трехмерной сферической области. Найдем девять наименьших значений λ и соответствующих им функций ϕ, удовлетворяющих Λϕ = λ ϕ, которые определяются следующим образом:

Новая функция DEigensystem в версии 10.3 позволяет вычислить требуемые собственные значения и функции следующим образом:

Собственные значения в этой задаче выражаются через BesselJZero. Вот пример:

Собственные значения можно визуализировать с помощью функции DensityPlot3D, которая возвращает красивые графики, как показано ниже:

УрЧП являются важным инструментом во многих отраслях науки и техники, в статистике и финансах. На более фундаментальном уровне они предоставляют точные математические формулировки некоторых самых глубоких и тонких вопросов о нашей Вселенной, скажем, о возможности существования голых сингулярностей. По моему опыту, изучение УрЧП награждает редким сочетанием из практических идей и интеллектуального удовлетворения.

Рекомендую изучить документацию по DSolve, NDSolve, DEigensystem, NDEigensystem и методу конечных элементов, чтобы узнать больше о различных подходах к решению УрЧП в Wolfram Language.

УрЧП в символьной форме поддерживаются в Wolfram Mathematica и Wolfram Language с версии 10.3, а в ближайшее время будут представлены и во всех остальных программных продуктах Wolfram.

Видео:МЗЭ 2022 Численное решение дифференциальных уравнений. Неявный метод Эйлера. Ложкин С.А.Скачать

Иллюстрированный самоучитель по Mathematica 3/4

Дифференциальные уравнения. Решение дифференциальных уравнений в символьном виде.

Несколько дифференциальных уравнений образуют систему дифференциальных уравнений. Решение таких систем также возможно средствами Mathematica и подробно описано в ряде книг по использованию системы. Дифференциальные уравнения и системы дифференциальных уравнений могут быть линейными и нелинейными. Для линейных уравнений обычно существуют решения в аналитическом виде. Нелинейные дифференциальные уравнения в общем случае аналитических решений не имеют, но могут решаться приближенными численными методами.

Дифференциальные уравнения широко используются в практике математических вычислений. Они являются основой при решении задач моделирования – особенно в динамике. Немногие математические системы имеют реализации численных методов решения систем дифференциальных уравнений. Но система Mathematica имеет средства как для символьного, так и для численного решения дифференциальных уравнений и их систем.

Для решения дифференциальных уравнений в символьном виде используются следующие средства:

DSolve[eqn, y[x], х] – решает дифференциальное уравнение относительно функций у [ х ] с независимой переменной х;
DSolve[, , ] – решает систему дифференциальных уравнений.

У функции DSolve и ее численного варианта NDSolve есть пара опций, на которые следует обратить внимание:

DSolveConstants – опция к DSolve, определяющая постоянные интегрирования, которые будут использованы в результате;
StartingStepSize – опция к NDSolve, определяющая величину начального шага.