В зависимости от природы проводника носителями электрического тока, т.е. частицами, которые переносят заряд в системе, могут быть электроны или ионы. В первом случае, когда электрическая проводимость обеспечивается электронами, вещества являются проводниками первого рода, к ним относятся металлы. К проводникам второго рода относятся растворы электролитов, расплавы, твердые электролиты, ионизированные газы. Перенос зарядов в таких системах связан с переносом вещества, поэтому прохождение электрического тока может вызывать изменения в проводниках с ионной проводимостью.
Способность проводника проводить электрический ток характеризуется его электрической проводимостьюL, которую можно определить как количество электричества, переносимого через сечение проводника в единицу времени при единичном напряжении. Электрическая проводимость численно обратна сопротивлению проводника R. Сопротивление
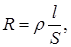
где r – удельная сопротивление проводника, l – длина проводника, S – площадь поперечного сечения проводника. Следовательно, электрическая проводимость
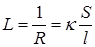
где k =1/r – удельная электрическая проводимость.
В случае растворов электролитов величина S представляет собою площадь электродов, между которыми находится раствор, а l – расстояние между ними.
Удельная электрическая проводимость k равна электрической проводимости проводника с единичными размерами (S = 1, l = 1), ее выражают в Ом –1 м –1 (основная единица), или См . м –1 (1 Ом –1 = 1 См – Сименс). Для растворов электролитов часто используется также выражение k в Ом –1 см –1 , т.е. k представляет электрическую проводимость 1 см 3 раствора, помещенного между плоскими параллельными электродами, находящимися на расстоянии 1 см друг от друга.
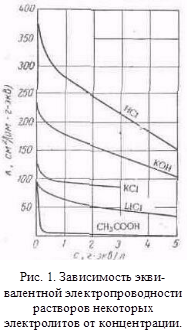
Удельная электрическая проводимость зависит от природы электролита и растворителя, температуры, концентрации электролита. На рисунке 17.1 приведен пример зависимости удельной электрической проводимости растворов некоторых электролитов от концентрации. В случае сильных электролитов характерным является наличие максимума на кривых зависимости k – c.
Это связано с тем, что при постоянных температуре и напряженности электрического поля электрическая проводимость обусловлена числом носителей зарядов, т.е. ионов, а также скоростью их перемещения. В области разбавленных растворов скорость движения ионов мало зависит от концентрации, и удельная электрическая проводимость возрастает почти прямо пропорционально концентрации. По мере увеличения концентрации усиливается межионное взаимодействие, возрастает плотность ионной атмосферы, что приводит к уменьшению скорости движения ионов. Этот эффект начинает преобладать над увеличением числа ионов, поэтому при высоких концентрациях удельная электрическая проводимость уменьшается.
В растворах слабых электролитов ионная концентрация невелика и скорость движения ионов мало зависит от концентрации, но с изменением концентрации изменяется степень диссоциации электролита, а следовательно, и концентрация ионов, которой и определяется величина удельной электрической проводимости.
Наряду с удельной электрической проводимостью используются также величины молярной электрической проводимости
Молярная электрическая проводимость– это проводимость раствора такого объема, в котором содержится один моль электролита, и раствор помещен между плоскими параллельными электродами, находящимися на единичном расстоянии друг от друга.
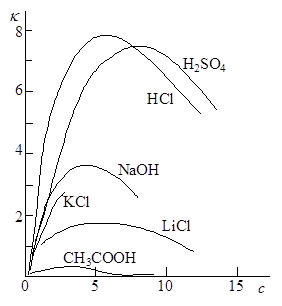 Рис. 17.1. Зависимость удельной электрической проводимости (Ом –1 см –1 10 –1 ) водных растворов некоторых электролитов от концентрации (моль/л) Рис. 17.1. Зависимость удельной электрической проводимости (Ом –1 см –1 10 –1 ) водных растворов некоторых электролитов от концентрации (моль/л) |
Основной единицей молярной электрической проводимости является Ом –1 ּм 2 ּмоль –1 , ей соответствует концентрация моль/м 3 . На практике в качестве единицы молярной электрической проводимости часто используют также Ом –1 см 2 моль –1 . Если выражать k в Ом –1 см –1 , а концентрацию в моль/л, то
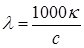
При определении численных значений l важно знать, молярная концентрация какой частицы рассматривается. Часто указывают электрическую проводимость частицы, которая соответствует ее химическому эквиваленту, т.е. концентрация выражается в единицах нормальности. Поэтому используется также понятие эквивалентной электрической проводимостиl*:
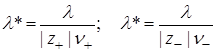
где n+ и n– – число катионов и анионов, образующихся при диссоциации молекулы, а z+ и z– – их заряды.
Например, концентрацию серной кислоты можно выражать в моль-экв/л, т.е. через концентрацию частиц 1/2 H2SO4, в этом случае
В случае 1–1-валентных электролитов l и l* совпадают.
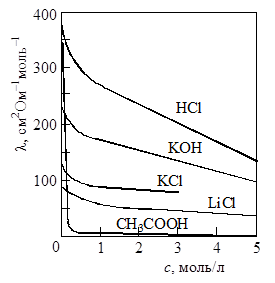 Рис. 17.2. Зависимость молярной электрической проводимости от концентрации электролита Рис. 17.2. Зависимость молярной электрической проводимости от концентрации электролита |
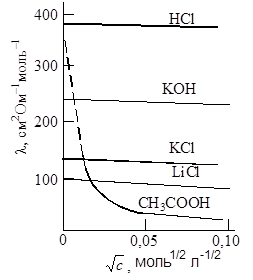 Рис. 17.3. Зависимость l от Рис. 17.3. Зависимость l от 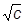 для водных растворов некоторых электролитов для водных растворов некоторых электролитов |
Молярная электрическая проводимость уменьшается при увеличении концентрации электролита (рис. 17.2). В растворах сильных электролитов это связано с тем, что при увеличении концентрации усиливается межионное взаимодействие и скорость движения ионов при этом уменьшается. Число ионов в разбавленных растворах при этом не изменяется, так как для определения молярной электрической проводимости всегда берется такой объем раствора, в котором находится 1 моль электролита. При значительных концентрациях возможна ионная ассоциация, приводящая к уменьшению числа токопроводящих частиц, и следовательно, к уменьшению электропроводности.
В случае слабых электролитов при возрастании концентрации уменьшается степень диссоциации, и число ионов в объеме раствора уменьшается.
Кольрауш экспериментально установил, что в области разбавленных растворов молярная электрическая проводимость линейно уменьшается с увеличением корня квадратного из концентрации (рис. 17.3), что выражается эмпирическим уравнением Кольрауша:
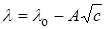
где lo – предельная молярная электрическая проводимость, т.е. электрическая проводимость при бесконечном разведении (l ® lo при c ® 0), A – эмпирическая константа, зависящая от природы раствора.
17.2. Подвижность ионов
Электрическая проводимость определяется числом ионов, которые проходят через поперечное сечение проводника в единицу времени. Общая сила тока I, проходящего через раствор, обусловлена тем количеством электричества, которое переносится в единицу времени катионами и анионами:
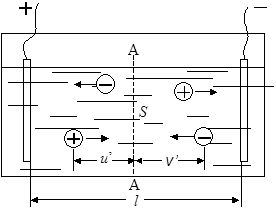 Рис. 17.4. Схема прохождения тока через раствор электролита Рис. 17.4. Схема прохождения тока через раствор электролита |
Рассмотрим прохождение тока в растворе электролита, который находится между электродами на расстоянии l см (рис. 17.4). Концентрация электролита в растворе c моль/см 3 , скорость движения катионов u¢ см/с, анионов – v¢ см/с при разности потенциалов между электродами E В. Выберем в объеме электролита некоторую воображаемую поверхность S см 2 . За одну секунду через эту поверхность пройдут все катионы, находящиеся слева от нее на расстоянии u¢ см и ближе, т.е. в объеме u¢S, и все анионы, находящиеся справа на расстоянии v¢ см и ближе, т.е. в объеме v¢S. Если степень диссоциации электролита a и из каждой молекулы образуется при диссоциации n+ катионов с зарядом z+ и n– анионов с зарядом z–, то в 1 см 3 раствора находится an+c молей катионов и an–c молей анионов, а в объемах u¢S и v¢S находится соответственно an+cu¢S молей катионов и an–cv¢S молей анионов. Так как один моль ионов переносит ziF кулонов электричества (F – число Фарадея), то сила тока
В силу электронейтральности раствора |z+n+| = |z–n–| и выражение (17.8) можно записать в виде:
При постоянных концентрации и температуре в условиях равномерного движения ионов можно считать, что их скорость зависит только от приложенной силы, т.е. она пропорциональна напряженности электрического поля E/l:
где коэффициенты u и v см 2 /(с . В) называются абсолютными подвижностямиионов и равны скоростям ионов при напряженности поля 1 В/см. Тогда сила тока
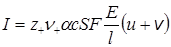
С другой стороны, по закону Ома
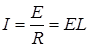
Подставив в это уравнение значение электрической проводимости L из уравнения (17.2) и выразив удельную электрическую проводимость k через молярную проводимость по уравнению (17.4), получим:
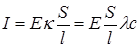
Приравняв полученное выражение и уравнение (17.11), приходим к зависимости молярной электрической проводимости от абсолютной подвижности ионов:
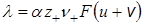
Введем величины подвижностей катионов U и анионов V:
Тогда молярная электрическая проводимость равна:
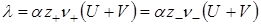
Для эквивалентной электрической проводимости, учитывая уравнение (17.5), получим:
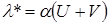
Для сильных электролитов степень диссоциации a = 1 и для них
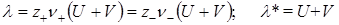
В случае слабых электролитов при бесконечном разбавлении (c®0) степень диссоциации a ® 1, а подвижности ионов достигают своих предельных значений Uo и Vo, и предельная молярная или эквивалентная электрические проводимости будут равны:
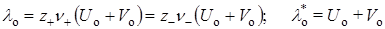
Последнее уравнение является выражением закона Кольрауша: эквивалентная электрическая проводимость при бесконечном разведении равна сумме предельных подвижностей ионов.
Предельная электрическая проводимость или предельные подвижности ионов являются важными константами, характеризующими способность данного электролита проводить электрический ток в растворе.
В таблице 17.1 приведены предельные подвижности некоторых ионов в водных растворах при 298,15 К. Из таблицы видно, что в ряду ионов с одинаковым зарядом (например, от Li + до Cs + ) подвижность возрастает с увеличением кристаллографического радиуса ионов. Согласно закону Стоксапри движении сферической частицы в вязкой среде ее скорость u равна:
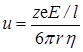
где r – эффективный радиус частицы, h – вязкость среды.
Предельные подвижности ионов (см 2 ·Ом –1 ·моль –1 )
в водных растворах при 298,15 К
H + 349,8 OH – 198,3
Na + 50,1 Cl – 76,4
Ag + 61,9 ClO3 – 64,6
1 /2Ba 2+ 63,6 HCOO – 54,6
Отсюда следует, что эффективные радиусы ионов в растворе отличаются от их радиусов в кристаллах. Это связано с тем, что в растворе ионы находятся в сольватированном состоянии. Если предположить, что сольватация обусловлена ион-дипольным взаимодействием, то количество молекул растворителя, связанных с ионом, и прочность связи зависят от напряженности поля, создаваемого ионом. При одинаковых зарядах напряженность поля тем выше, чем меньше радиус иона, и следовательно, степень сольватации будет больше. Поэтому ион Li + гидратирован в большей степени, чем ион К + или Сs + .
Обращает на себя внимание чрезвычайно высокая по сравнению с другими ионами подвижность ионов водорода и гидроксила. Согласно современным представлениям, аномальная подвижность этих ионовобязана особому эстафетному, или цепному, механизму переноса протона. Поскольку в воде ионы водорода находятся в виде ионов гидроксония Н3О + , протон может переходить к соседней молекуле воды. В электрическом поле наиболее вероятен переход в направлении поля и процесс перемещения протона можно представить по схеме:


Аналогично можно представить и перемещение ионов гидроксила:


Более высокая подвижность ионов водорода по сравнению с ионами ОН – связана с тем, что отрыв протона от иона Н3О + требует меньшей энергии активации, чем его отрыв от молекулы воды.
Подвижность ионов в значительной степени зависит от температуры. Температурную зависимость электрической проводимости можно представить уравнением вида
где a, b, c – эмпирические коэффициенты.
17.3. Зависимость молярной электрической проводимости
от концентрации
Скорости движения ионов зависят от межионного взаимодействия. В электрическом поле в зависимости от знака заряда ионы перемещаются по полю или против него, в результате чего ион и его ионная атмосфера движутся в разных направлениях. Ионы при движении увлекают также соседние молекулы растворителя, все это приводит к тому, что оба потока вызывают взаимное торможение, и скорость движения ионов уменьшается (рис. 17.5). Это явление получило название электрофоретического (катафоретического) эффекта.
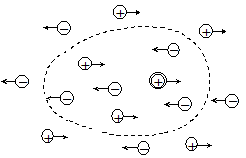 Рис. 17.5. Схема движения центрального иона и ионной атмосферы в электрическом поле Рис. 17.5. Схема движения центрального иона и ионной атмосферы в электрическом поле |
При перемещении иона непрерывно происходит разрушение прежней ионной атмосферы и образование новой. Хотя эти процессы протекают достаточно быстро, все же восстановление сферической симметрии ионной атмосферы после смещения центрального иона в новое положение происходит с некоторым запаздыванием. Нарушение симметрии ионной атмосферы ведет также к дополнительному торможению движения ионов. Этот эффект носит название релаксационного (эффектаасимметрии).
Оба эффекта проявляются в тем большей степени, чем выше концентрация электролита, что приводит к снижению молярной электрической проводимости с ростом концентрации.
Математическая трактовка эффектов основана на теории межионных электростатических взаимодействий и гидродинамическом уравнении потока. Первые приближенные расчеты были проведены Дебаем и Гюккелем, а затем более подробно Онзагером, который установил связь между молярной электрической проводимостью и концентрацией. В частности, для 1–1-валентных электролитов в разбавленных растворах предельный закон Онзагераможно представить в виде уравнения:
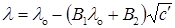
где коэффициент В1 характеризует релаксационный эффект и зависит от диэлектрической проницаемости e и температуры, а коэффициент В2 характеризует электрофоретический эффект и зависит от диэлектрической проницаемости, температуры и вязкости среды h. Для бинарных одновалентных электролитов в водном растворе
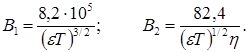
В уравнении (17.20) величина c¢ представляет ионную концентрацию, поэтому для растворов слабых электролитов предельный закон Онзагера можно представить в виде:
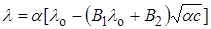
Отношение молярных электрических проводимостей при некоторой определенной концентрации и бесконечном разведении называется коэффициентом электропроводности
и для растворов электролитов
В разбавленных растворах слабых электролитов межионные электростатические взаимодействия малы и можно считать, что fl » 1, тогда l = alo, что совпадает с выражением, полученным в классической теории электролитической диссоциации Аррениуса, согласно которой степень диссоциации
Таким образом, резкое уменьшение молярной электрической проводимости при увеличении концентрации в разбавленных растворах слабых электролитов обусловлено, главным образом, уменьшением степени диссоциации. В разбавленных растворах сильных электролитов a = 1 и уменьшение проводимости связано с уменьшением коэффициента электропроводности. Так как fl изменяется с концентрацией медленнее, чем a для слабых электролитов, то и уменьшение l при увеличении концентрации в разбавленных растворах сильных электролитов происходит медленнее, чем в растворах слабых электролитов.
17.4. Эффекты Вина и Дебая – Фалькенгагена
Справедливость представлений Дебая и Гюккеля о межионном взаимодействии была подтверждена экспериментально.
В 1927 г. Вин обнаружил рост электрической проводимости в растворах сильных электролитов при высоких напряженностях электрического поля (» 10 5 В/см) – первый эффект Вина. Это явление связано с тем, что в таких полях скорость движения ионов очень высока и ионная атмосфера вокруг иона не образуется. В этих условиях и электрофоретический и релаксационный эффекты отсутствуют. С ростом напряженности электрического поля электрическая проводимость увеличивается до предельного значения.
Повышение электрической проводимости наблюдается также в растворах слабых электролитов при увеличении напряженности поля. Этот второй эффект Вина указывает на то, что в электрическом поле степень диссоциации электролита увеличивается.
В 1928 г. Дебай и Фалькенгаген теоретически предсказали, что асимметрия ионной атмосферы исчезает в полях высокой частоты, если период колебания электрического поля сопоставим со временем релаксации ионной атмосферы. Исчезновение релаксационного эффекта должно привести к повышению электрической проводимости. Согласно теории Дебая – Фалькенгагена время релаксации q (т.е. время, за которое ионная атмосфера исчезает после удаления центрального иона или образуется вокруг него в новой точке) зависит от концентрации:
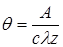
где A – постоянная для данного растворителя и температуры.
Частота, при которой должен проявляться эффект повышения электрической проводимости n = 1/q. Для водного раствора 1–1-валентного электролита при c = 10 –3 моль/л эта частота равна примерно 10 9 с –1 .
Действительно, эффект Дебая – Фалькенгагена(частотный эффект, или эффект дисперсии электропроводности) был обнаружен экспериментально при частотах около 1 МГц и выше, при которых молярная электрическая проводимость увеличивалась, но она не достигала предельного значения lo, так как электрофоретический эффект в этих условиях сохранялся. Из опытного сопоставления эффектов Вина (полное исчезновение ионной атмосферы) и Дебая – Фалькенгагена (исчезновение симметрии ионной атмосферы) следует, что электрофоретический эффект примерно в два раза сильнее релаксационного.
17.5. Электрическая проводимость неводных растворов
Ряд общих закономерностей, характерных для водных растворов, сохраняется и при переходе к другим растворителям, но проявляются также и специфические особенности растворителей. Одними из основных характеристик растворителя, влияющих на электрическую проводимость, являются его диэлектрическая проницаемость и вязкость. Количественно связь электрической проводимости с вязкостью растворителя ho выражается правилом Писаржевского – Вальдена:
Это правило приближенное и достаточно хорошо выполняется лишь в случае больших ионов, размеры которых значительно больше молекул растворителя.
Диэлектрическая проницаемость влияет на силу кулоновского взаимодействия между ионами и, следовательно, на степень диссоциации и ионную концентрацию.
Впервые в работах И.А.Каблукова, а затем других исследователей (Саханов, Вальден, Фуосс и Краус) было установлено, что в неводных растворителях при увеличении концентрации (уменьшении разбавления) до некоторой величины молярная электрическая проводимость начинает возрастать. Это явление получило название аномальной электрической проводимости. На кривой зависимости l от разведения обнаруживается минимум. На основании экспериментальных данных Вальден установил, что величина разведения j, при котором наблюдается минимум, связана с диэлектрической проницаемостью растворителя соотношением
ej 1/3 = const. (17.30)
Объяснение аномальной электрической проводимости базируется на представлениях об ассоциации в растворах электролитов. Согласно Саханову, в концентрированных растворах могут образовываться ассоциаты молекул, которые распадаются на комплексные ионы, проводящие электрический ток, т.е. существуют равновесия:
xКА L (КА)x L 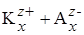
В. К. Семенченко и Н. Бьеррум указали на возможность образования ионных пар в результате кулоновского взаимодействия. Возникновение ионных пар, которые проявляют свойства незаряженных молекул, должно приводить к быстрому снижению молярной электрической проводимости с повышением концентрации. Особенно заметно этот эффект должен проявляться в растворителях с низкой диэлектрической проницаемостью.
В концентрированных растворах могут образовываться более сложные агрегаты, в частности, ионные тройники. Ионные двойники К + А – , присоединяя катион К + или анион А – , образуют тройники К + А – К + или А – К + А – , что увеличивает электрическую проводимость.
17.6. Числа переноса
Вследствие различной подвижности ионов количество электричества, переносимое катионами и анионами электролита, различно. Числом переноса ti называют долю тока, которая переносится данным сортом ионов:
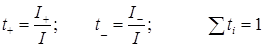
Из уравнений (17.7), (17.8) и (17.15) получим для бинарного электролита:
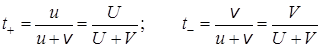
Как видно из этих выражений, число переноса данного сорта ионов зависит от подвижности обоих ионов и характеризует не отдельно взятый вид ионов, а весь электролит в целом. Так как подвижности ионов зависят от концентрации, то от нее зависят и числа переноса. В качестве примера в таблице 17.2 приведены числа переноса катионов в водных растворах некоторых электролитов при температуре 25 о С.
На основании экспериментальных данных установлено, что если число переноса иона близко к 0,5, то оно мало зависит от концентрации, при t+ 0,5 растет), а при t–> 0,5 – повышается (t+ + или растворы KCl и KNO3 при определении чисел переноса ионов Cl – . Плотность нижнего раствора должна быть больше плотности верхнего (этого можно достичь добавлением неэлектролита). Раствор с исследуемым электролитом помещают ближе к электроду, к которому будет перемещаться граница. При прохождении через растворы Q кулонов электричества граница перемещается на расстояние l, т.е. через сечение S ячейки прошли ионы, находящиеся в объеме aбвг, равном lS, тогда число переноса иона
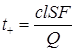
где c – концентрация раствора исследуемого электролита.
В случае окрашенных растворов за перемещением границы можно наблюдать визуально, в случае бесцветных растворов – по показателю преломления или какому-либо другому свойству.
17.7. Измерение электрической проводимости растворов
электролитов
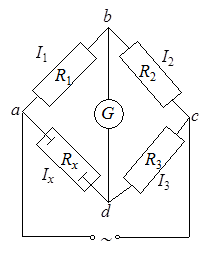 Рис. 17.8. Принципиальная схема прибора для определения электрической проводимости Рис. 17.8. Принципиальная схема прибора для определения электрической проводимости |
В основе приборов для определения электрической проводимости лежит мостовая схема (рис. 17.8). В одно из плеч моста включается ячейка с исследуемым раствором, имеющим сопротивление Rx. Ячейка представляет собой стеклянный сосуд с двумя платиновыми электродами, закрепленными на определенном расстоянии друг от друга. Чтобы исключить поляризацию электродов (т.е. изменение состояния поверхности электродов и концентрации электролита около электродов) их покрывают платиновой чернью, а для питания используют обычно переменный ток.
Установив определенную величину сопротивления R3, подбирают сопротивления R1 и R2 так, чтобы ток не проходил на участке ab. В момент, когда нуль-инструмент G (гальванометр, осциллограф) показывает отсутствие тока, согласно закону Кирхгофа
Отсюда следует, что
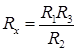
По значениям Rx рассчитывают удельную электрическую проводимость раствора:
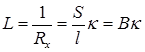
где В – постоянная ячейки, зависящая от площади электродов S и расстояния между ними l. Величину В определяют путем измерения сопротивления раствора с известной удельной электрической проводимостью. Обычно для этих целей используют растворы хлорида калия (таблица 17.3). После определения постоянной ячейки на основании определения сопротивления исследуемых растворов рассчитывают удельную и молярную электрическую проводимость этих растворов в соответствии с уравнениями (17.1) и (17.2).
Удельная электрическая проводимость стандартных водных
растворов хлорида калия
| c, моль/л | г KCl на 1000 г раствора | k при различных температурах, Ом –1 см –1 | ||
| 273,15 К | 291,15 К | 298,15 К | ||
| 1,0 | 71,1352 | 0,06521 | 0,09789 | 0,11140 |
| 0,1 | 7,41913 | 0,007141 | 0,011172 | 0,012862 |
| 0,01 | 0,745263 | 0,0007740 | 0,0012211 | 0,0014094 |
17.8. Кондуктометрическое титрование
Методы исследования свойств растворов электролитов, основанные на определении электрической проводимости, называются кондуктометрическими (кондуктометрией). Наиболее часто кондуктометрияиспользуется для определения концентрации растворов электролитов (кондуктометрическое титрование), определения констант диссоциации (или ионной ассоциации) электролитов, в физико-химическом анализе.
При кондуктометрическом титровании строят кривые титрования – зависимость электрической проводимости раствора от объема титранта, добавляемого к исследуемому раствору в процессе титрования. При этом можно использовать реакции нейтрализации, осаждения, комплексообразования и др. Точку эквивалентности определяют по излому на кривой титрования. Кондуктометрическое титрование можно использовать в случае окрашенных или мутных растворов, когда применение индикаторов затруднено или невозможно.
В качестве примера рассмотрим изменение электрической проводимости раствора в процессе реакции нейтрализации (кислотно-основное титрование). Если титровать сильную кислоту (например, НСl) сильным основанием (NaOH), ионы Н3О + , реагируя с ионами ОН – , образуют практически недиссоциируемые молекулы воды, а в растворе вместо ионов Н3О + появляется эквивалентное количество ионов Na + . Так подвижность ионов натрия значительно меньше подвижности ионов водорода, электрическая проводимость раствора резко уменьшается (рис. 17.9, участок ab). Количество ионов хлора в процессе титрования остается неизменным и они практически не влияют на изменение электрической проводимости. После достижения точки эквивалентности b при дальнейшем добавлении щелочи проводимость увеличивается (участок bc) за счет общего возрастания ионной концентрации – ионов Na + и ОН – . Подвижность ионов ОН – также значительно больше подвижности других ионов, поэтому наблюдается резкое увеличение электрической проводимости, хотя наклон прямой bc все же меньше по абсолютному значению, чем наклон прямой ab.
Рис.17.9. Кривая кондуктометрического- Рис.17.10. Кривая кондуктометрического
титрования сильной кислоты титрования слабой кислоты
сильным основанием сильным основанием
В случае титрования слабой кислоты, например, уксусной, сильным основанием (рис. 17.10) до точки эквивалентности происходит некоторое увеличение электрической проводимости (участок ab), так как в этом случае вместо слабо диссоциирующей кислоты СН3СООН образуется эквивалентное количество хорошо диссоциирующей соли СН3СООNа и ионная концентрация возрастает. После точки эквивалентности b сильное увеличение электрической проводимости обусловлено, как и в предыдущем случае, накоплением в растворе ионов ОН – с высокой подвижностью и ионов Nа + .
Подобные же кривые титрования получаются при реакциях с образованием труднорастворимых соединений или плохо проводящих ток комплексных ионов. Величина и знак наклонов обеих ветвей кривой титрования зависят от электрической проводимости титруемого вещества, титранта и продуктов титрования.
17.9. Определение констант диссоциации
В первом приближении степень диссоциации a можно вычислить из соотношения a = l/lo. Подставив это значение в уравнение закона разведения Оствальда, получим:
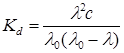
Таким образом, для вычисления константы диссоциации экспериментально определяют молярную электрическую проводимость l, а значения lo получают из суммы предельных подвижностей ионов. В случае отсутствия таких данных можно использовать предложенный Краусом и Бреемграфический метод. Уравнение (17.38) можно преобразовать к виду:
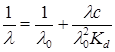
Это уравнение прямой в координатах 1/l – lc с тангенсом угла наклона, равным 1/ 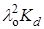
Уравнение (17.43) основано на теории диссоциации Аррениуса и не учитывает межионного взаимодействия. Фактически степень диссоциации должна рассчитываться не по приближенному уравнению (17.27), а по соотношению (17.26) с учетом коэффициента электрической проводимости.
Фуосс и Крауспредложили для определения констант диссоциации уравнение
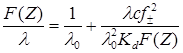
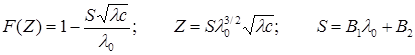
коэффициенты В1 и В2 имеют те же значения, что и в уравнении Онзагера (17.23).
Расчет ведется методом последовательных приближений. Вначале, построив график 1/l – lc, находят приближенное значение lo и рассчитывают функцию F(Z). Затем рассчитывают степень диссоциации a = l/loF(Z) и коэффициент активности f± по уравнению Дебая–Гюккеля при ионной концентрации ac. По полученным данным строят график зависимости F(Z)/l от lcf±/F(Z) и находят более точное значение lo. Расчет повторяют до получения прямолинейной зависимости и по тангенсу угла наклона прямой вычисляют константу диссоциации.
В настоящее время предложено также ряд других уравнений для определения констант диссоциации по кондуктометрическим данным.
| | | следующая лекция ==> | |
| Уравнение Максвелла в в дифференциальной форме. | | | Потрібна кількість форсунок |
Дата добавления: 2015-12-16 ; просмотров: 6450 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Электрическое сопротивление проводника, удельное сопротивление проводника, реостатСкачать

Взаимосвязь удельной и молярной электропроводности уравнение
ФИЗИЧЕСКАЯ И КОЛЛОИДНАЯ ХИМИЯ
Конспект лекций для студентов биофака ЮФУ (РГУ)
3.4 ЭЛЕКТРОПРОВОДНОСТЬ РАСТВОРОВ ЭЛЕКТРОЛИТОВ
3.4.1 Удельная электропроводность растворов электролитов
Электрический ток есть упорядоченное перемещение заряженных частиц. Растворы электролитов обладают ионной проводимостью (являются т.н. проводниками второго рода), т.е. электропроводность растворов электролитов обусловлена перемещением ионов в электрическом поле (в отличие от электронной проводимости проводников первого рода).
Величина преимущественного передвижения иона в направлении одного из электродов при прохождении тока через раствор отнесённая к градиенту потенциала 1 В/см, есть абсолютная скорость движения иона . Абсолютные скорости движения ионов имеют величины порядка 0,0005 – 0,003 см 2 /(В·с). Абсолютные скорости движения катионов U+ и анионов U– различаются; это приводит к тому, что ионы разных знаков переносят разные количества электричества.
Всякий проводник, по которому течет ток, представляет для него определенное сопротивление R, которое, согласно закону Ома, прямо пропорционально длине проводника l и обратно пропорционально площади сечения S; коэффициентом пропорциональности является удельное сопротивление материала ρ – сопротивление проводника, имеющего длину 1 см и сечение 1 см 2 :

В качестве количественной меры способности раствора электролита проводить электрический ток используют обычно удельную электропроводность κ (каппа) – величину, обратную удельному сопротивлению (т.е. величину, обратную сопротивлению столба раствора между электродами площадью 1 см 2 , находящимися на расстоянии 1 см):

Величина удельной электропроводности электролита зависит от ряда факторов: природы электролита, температуры, концентрации раствора. Удельная электропроводность растворов электролитов (в отличие от электропроводности проводников первого рода) с увеличением температуры возрастает, что вызвано увеличением скорости движения ионов за счет понижения вязкости раствора и уменьшения сольватированности ионов. Зависимость удельной электропроводности от концентрации раствора представлена на рис. 3.9.
Рис. 3.9 Зависимость удельной электропроводности электролитов от концентрации
(1 – H2SO4, 2 – KOH, 3 – CH3COOH)
Как видно из рисунка, с увеличением концентрации удельная электропроводность растворов сначала возрастает, достигая некоторого максимального значения, затем начинает уменьшаться. Эта зависимость очень чётко выражена для сильных электролитов и значительно хуже для слабых. Наличие максимума на кривых объясняется тем, что в разбавленных растворах сильных электролитов скорость движения ионов мало зависит от концентрации, и κ сначала растет почти прямо пропорционально числу ионов; с ростом концентрации усиливается взаимодействие ионов, что уменьшает скорость их движения. Для слабых электролитов наличие максимума на кривой обусловлено тем, что с ростом концентрации уменьшается степень диссоциации, и при достижении определенной концентрации число ионов в растворе начинает увеличиваться медленнее, чем концентрация. Для учета влияния на электрическую проводимость растворов электролитов их концентрации и взаимодействия между ионами введено понятие молярной электропроводности раствора.
3.4.2 Молярная электропроводность растворов электролитов
Молярная электропроводность раствора λ есть величина, обратная сопротивлению раствора, содержащего 1 моль растворенного вещества и помещенного между электродами, расположенными на расстоянии 1 см друг от друга. С удельной электропроводностью κ и молярной концентрацией раствора С молярная электропроводность связана следующим соотношением:

Молярная электропроводность как сильных, так и слабых электролитов увеличивается с уменьшением концентрации (т.е. увеличением разведения раствора V = 1/С), достигая некоторого предельного значения λ o, называемого молярной электропроводностью при бесконечном разведении (рис. 3.10 – 3.11).
Рис. 3.10 Зависимость молярной Рис. 3.11 Зависимость молярной
электропроводности от концентрации. электропроводности от разведения
Для слабого электролита такая зависимость молярной электропроводности от концентрации обусловлена в основном увеличением степени диссоциации с разбавлением раствора. В случае сильного электролита с уменьшением концентрации ослабляется взаимодействие ионов между собой, что увеличивает скорость их движения и, следовательно, молярную электропроводность раствора. Последнюю связывает с абсолютными скоростями движения катионов и анионов U+ и U– уравнение Аррениуса (III.35):

Ф. Кольрауш показал, что в молярную электропроводность бесконечно разбавленных растворов электролитов каждый из ионов вносит свой независимый вклад, и λ o является суммой молярных электропроводностей катиона и аниона λ + и λ – (т.н. подвижностей ионов), и сформулировал закон независимости движения ионов :
Молярная электропроводность при бесконечном разведении равна сумме электролитических подвижностей катиона и аниона данного электролита.

Подставив в это выражение уравнение Аррениуса (III.35) и приняв, что при бесконечном разведении степень диссоциации α равна единице, получим:



Электролитическая подвижность является важнейшей характеристикой иона, отражающей его участие в электропроводности раствора.
Copyright © С. И. Левченков, 1996 — 2005.
Видео:Электропроводность сильных и слабых электролитовСкачать

Реферат: Электропроводность электролитов
| Название: Электропроводность электролитов Раздел: Рефераты по химии Тип: реферат Добавлен 03:21:48 23 августа 2005 Похожие работы Просмотров: 9683 Комментариев: 18 Оценило: 6 человек Средний балл: 4.5 Оценка: 5 Скачать |
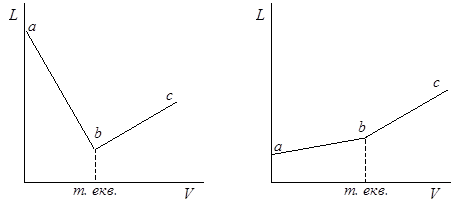


 Эквивалентная электропроводность — это электропроводность такого объема (φ см 3 ) раствора, в котором содержится 1 г-экв растворенного вещества, причем электроды находятся на расстоянии 1 см друг от друга. Учитывая сказанное выше относительно удельной электропроводности, можно представить себе погруженные в раствор параллельные электроды на расстоянии 1 см., имеющие весьма большую площадь. Мы вырезаем мысленно на поверхности каждого электрода вдали от его краев площадь, равную φ-см 2 . Электропроводность раствора, заключенного между выделенными поверхностями таких электродов, имеющими площадь, равную φ- см 2 , и есть эквивалентная электропроводность раствора. Объем раствора между этими площадями электродов равен, очевидно, φ-см 3 и содержит один грамм-эквивалент соли. Величина φ, равная 1000/с см 3 /г-экв, называется разведением. Между электродами, построенными указанным выше способом, при любой концентрации электролита находится 1 г-экв растворенного вещества и изменение эквивалентной электропроводности, которое обусловлено изменением концентрации, связано с изменением числа ионов, образуемых грамм-эквивалентом, т. е. с изменением степени диссоциации, и с изменением скорости движения ионов, вызываемым ионной атмосферой.
Эквивалентная электропроводность — это электропроводность такого объема (φ см 3 ) раствора, в котором содержится 1 г-экв растворенного вещества, причем электроды находятся на расстоянии 1 см друг от друга. Учитывая сказанное выше относительно удельной электропроводности, можно представить себе погруженные в раствор параллельные электроды на расстоянии 1 см., имеющие весьма большую площадь. Мы вырезаем мысленно на поверхности каждого электрода вдали от его краев площадь, равную φ-см 2 . Электропроводность раствора, заключенного между выделенными поверхностями таких электродов, имеющими площадь, равную φ- см 2 , и есть эквивалентная электропроводность раствора. Объем раствора между этими площадями электродов равен, очевидно, φ-см 3 и содержит один грамм-эквивалент соли. Величина φ, равная 1000/с см 3 /г-экв, называется разведением. Между электродами, построенными указанным выше способом, при любой концентрации электролита находится 1 г-экв растворенного вещества и изменение эквивалентной электропроводности, которое обусловлено изменением концентрации, связано с изменением числа ионов, образуемых грамм-эквивалентом, т. е. с изменением степени диссоциации, и с изменением скорости движения ионов, вызываемым ионной атмосферой.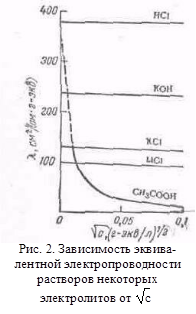 из графика (Рис. 2), для сильных электролитов соблюдается медленное линейное уменьшение λ с увеличением , что соответствует эмпирической формуле Кольрауша (1900);
из графика (Рис. 2), для сильных электролитов соблюдается медленное линейное уменьшение λ с увеличением , что соответствует эмпирической формуле Кольрауша (1900);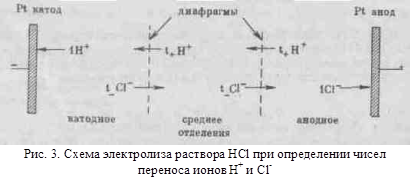 Таким образом, в результате протекания через электролизер одного фарадея электричества содержание НС1 в катодном отделении уменьшилось на t— г/моль.
Таким образом, в результате протекания через электролизер одного фарадея электричества содержание НС1 в катодном отделении уменьшилось на t— г/моль.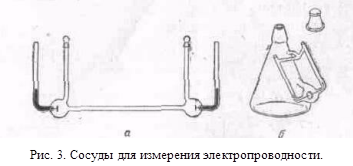 Поляризацию можно устранить платинированием платиновых электродов (т. е. покрытием их путем электролиза тонким слоем платиновой черни и, таким образом, увеличением поверхности электродов) и применением переменного тока с частотой 500—2000 гц для устранения концентрационной поляризации. Для измерения электропроводности используют сосуды самой различной формы. Сосуд снабжен двумя одинаковыми плоскими параллельными электродами, закрепленными так, чтобы расстояние между ними не изменялось. .На рис. 3 показаны формы сосудов, рекомендуемых для определения электропроводности при больших (рис. 3,а) и при малых (рис. 3,б) концентрациях.
Поляризацию можно устранить платинированием платиновых электродов (т. е. покрытием их путем электролиза тонким слоем платиновой черни и, таким образом, увеличением поверхности электродов) и применением переменного тока с частотой 500—2000 гц для устранения концентрационной поляризации. Для измерения электропроводности используют сосуды самой различной формы. Сосуд снабжен двумя одинаковыми плоскими параллельными электродами, закрепленными так, чтобы расстояние между ними не изменялось. .На рис. 3 показаны формы сосудов, рекомендуемых для определения электропроводности при больших (рис. 3,а) и при малых (рис. 3,б) концентрациях.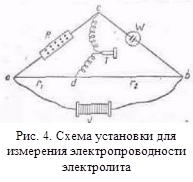 Схема установки для определения электропроводности показана на рис. 4. Прибор представляет собою контур обе. Между b и с в цепь включен сосуд для измерения электропроводности. Сопротивление его обозначено через W, между а и с—магазин сопротивления R . Отрезок ab представляет собой тонкую металлическую (Pt, Mn, манганиновую и т. п.) однородную проволоку длиной в 1 м, натянутую на линейку с делениями. В точках а и b подсоединяются провода, по которым подается переменный ток от вторичной обмотки катушки Румкорфа v или от генератора звуковой частоты. Для определения сопротивления жидкостей применяют переменный ток, а не постоянный во избежание электролиза и поляризации. При переменном токе очень чувствительным инструментом, обнаруживающим присутствие или отсутствие тока. является низкоомный телефон (в последнее время применяется катодный осциллограф). Телефон включается между точкой с и подвижным контактом d .
Схема установки для определения электропроводности показана на рис. 4. Прибор представляет собою контур обе. Между b и с в цепь включен сосуд для измерения электропроводности. Сопротивление его обозначено через W, между а и с—магазин сопротивления R . Отрезок ab представляет собой тонкую металлическую (Pt, Mn, манганиновую и т. п.) однородную проволоку длиной в 1 м, натянутую на линейку с делениями. В точках а и b подсоединяются провода, по которым подается переменный ток от вторичной обмотки катушки Румкорфа v или от генератора звуковой частоты. Для определения сопротивления жидкостей применяют переменный ток, а не постоянный во избежание электролиза и поляризации. При переменном токе очень чувствительным инструментом, обнаруживающим присутствие или отсутствие тока. является низкоомный телефон (в последнее время применяется катодный осциллограф). Телефон включается между точкой с и подвижным контактом d .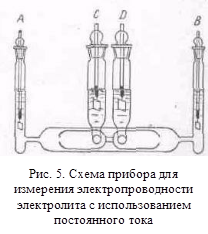 Использование переменного тока позволяет измерять электропроводность электролитов с высокой точностью, но при этом возникают затруднения, связанные с наличием электрической емкости и самоиндукции (особенно первой) в электрической схеме, тогда как необходимо измерять толькоомическое сопротивление. При использовании постоянного тока перечисленные затруднения отпадают, но возникает концентрационная поляризация. Чтобы избежать появления концентрационной поляризации, измеряют разность потенциалов между специальными, строго обратимыми электродами, расположенными на значительном расстоянии от питающих электродов. Современная потенциометрия позволяет измерять Е с точностью до 0,0001%. На рис. 5 изображен один из сосудов, где С и D — электроды для измерения разности потенциалов, а А и B — питающие электроды. Измеряется разность потенциалов Е, при токе постоянной силы между электродами А и B и разность потенциалов Ео на концах точно известного сопротивления Wo , включенного последовательно с сосудом; очевидно, искомое сопротивление W1 определяется из соотношения
Использование переменного тока позволяет измерять электропроводность электролитов с высокой точностью, но при этом возникают затруднения, связанные с наличием электрической емкости и самоиндукции (особенно первой) в электрической схеме, тогда как необходимо измерять толькоомическое сопротивление. При использовании постоянного тока перечисленные затруднения отпадают, но возникает концентрационная поляризация. Чтобы избежать появления концентрационной поляризации, измеряют разность потенциалов между специальными, строго обратимыми электродами, расположенными на значительном расстоянии от питающих электродов. Современная потенциометрия позволяет измерять Е с точностью до 0,0001%. На рис. 5 изображен один из сосудов, где С и D — электроды для измерения разности потенциалов, а А и B — питающие электроды. Измеряется разность потенциалов Е, при токе постоянной силы между электродами А и B и разность потенциалов Ео на концах точно известного сопротивления Wo , включенного последовательно с сосудом; очевидно, искомое сопротивление W1 определяется из соотношения
















