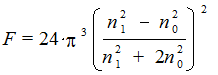Взаимосвязь показателя степени n в уравнении геллера и параметра z (8 видео)

Содержание

Оптические методы исследования дисперсных систем
2.4.6. Определение размера частиц в коллоидных системах оптическим методом
Определение размеров частиц дисперсных систем турбидиметрическим методом. Константы, не зависящие от длины волны
Страницы работы
Фрагмент текста работы
Руководитель: доцент ______________ / /
🎥 Видео

Видео:Математика это не ИсламСкачать

Оптические методы исследования дисперсных систем

Оптические методы принадлежат к самым распространенным методам исследования веществ и материалов. В коллоидной химии оптические методы используются для изучения состава и структуры поверхностных слоев, а так же структуры дисперсных систем — формы, дисперсности, пористости, строения элементов структуры (отдельных частиц), профиля поверхности, толщины слоев, их состава и природы сил взаимодействующих компонентов при адсорбции и адгезии, структуры слоев и ее дефектов, механических, электрических и других свойств. Эти исследования имеют огромное значение для катализа, коррозии, адсорбции, адгезии, трения и других практически важных процессов.

К классическим методам исследования дисперсных систем, использующим явление светорассеяния, принадлежит турбидиметрия, основанная на способности систем ослаблять интенсивность проходящего света. В этом случае измерения ведут с помощью обычных спектрофотометров, позволяющих определить оптическую плотность или светопропусканис и вычислить мутность системы.

Выражение характеризует долю света, прошедшего через систему, поэтому называется светопропусканием П. Степень ослабления интенсивности света характеризует отношение , которое в логарифмической форме называется светопоглощением Q, то есть

Светопропускание и светопоглощение связаны между собой и если их выразить в процентах, то

Тогда уравнение (3.4) можно записать в виде 2,3Q = т-1, откуда

Для дисперсной фазы, имеющей размеры частиц, соизмеримые с длиной волны падающего света и больше, закономерности рассеяния света значительно усложняются и перестают соответствовать закону Релея. Интенсивность рассеяния при этом слабее зависит от длины волны падающего света, и показатель степени п в выражении для интенсивности рассеянного света I р

4 меняется от 4 для частиц малого размера (реле-

евское рассеяние) до нуля (отражение света частицами, не зависящее от длины волны).

Уравнение Релея может быть использовано для определения размеров частиц сферической формы, если их радиус г не превышает 1/20 длины волны падающего света Л. Необходимым условием его использования является отсутствие поглощения света, а так же вторичного светорассения. Поэтому уравнение Релея применимо только для так называемых «белых золей», то есть непоглощающих свет дисперсных систем, и при очень малых концентрациях дисперсной фазы.

Если размер частиц (радиус) составляет от 1/20 до 1/6 длины световой волны и показатели преломления частиц и среды нс сильно различаются, для описания светорассеяния в системе можно воспользоваться уравнением Геллера:

где к и к’ — константы уравнения, не зависящие от длины волны; п — показатель степени, который называют показателем дисперсности.

В зависимости от размера частиц дисперсной фазы величина показателя степени (показателя дисперсности) в уравнении Геллера, как и в законе Релея, может изменяться от 1 до 4.

В логарифмической форме уравнение (3.6) для оптической плотности имеет вид прямой линии:

Сведение уравнения к прямой составляет суть линеаризации, удобной для обработки экспериментальных результатов. На графике 1пГ)д = /(In Л) по углу наклона прямой к оси абсцисс находят величину

показателя степени п (рис. 3.3).

Рис. 3.3. Уравнение Геллера в спрямленных координатах

Из рис. 3.3 видно, что

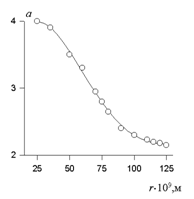
На графике, который называется калибровочной кривой Геллера и показывает зависимость величины п от размера частицы (рис. 3.4), по известному значению показателя п находят размер частиц золя.

Использование стандартной программы Excel позволяет быстро находить коэффициенты уравнения , выполнять аппроксимацию и сглаживать линию тренда, оценивая величину достоверности результатов.

Характер зависимости п от размера частиц г был определен Геллером эмпирически. Как и уравнение Релся, этот метод применим только для «белых золей», то есть для неокрашенных дисперсных систем (метод базируется только на светорассеянии).

Экспериментально полученная кривая Геллера показывает взаимосвязь показателя степени при длине волны с размером частиц дисперсной фазы, она используется как калибровочная в тех случаях, когда дисперсная система по своим физико-химическим свойствам и по степени дисперсности близка к тем, для которых зависимость получена, то есть входит в понятие «белые золи». В других случаях необходимо строить собственную калибровочную зависимость.

Показатель дисперсности п зависит от соотношения между размером частицы d и длиной волны падающего света Л, которое характеризует безразмерный параметр Z:

Рис. 3.4. Зависимость показателя дисперсности от радиуса частиц

С увеличением Z значение п уменьшается, стремясь в пределе к 2 для частиц, радиус которых больше длины волны.

При малых значениях Z уравнение Геллера переходит в уравнение Рслея (п —> 4). Значения п для Z от 2 до 8 приведены в табл. 3.1.

Показатель степени дисперсности п в уравнении Геллера в зависимое! н от параметра Z

Видео:Когда тренер - твой друг😏Скачать

2.4.6. Определение размера частиц в коллоидных системах оптическим методом

Оптический метод определения размера частиц в «белых» золях, т.е. коллоидных системах не поглощающих свет, основано на использовании уравнения Рэлея (2.2.103). Учитывая, что объемная доля частиц

j = n v₁/ V = C /r, (2.2.112)

где n – число частиц в 1 см 3 золя или латекса; 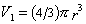– объем одной сферической частицы; С – массовая концентрация, г/см 3 ;r – плотность полимера, г/cм 3 ; r – радиус частиц, см.

Из уравнения Рэлея можем получить

, (2.2.113)

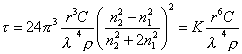
где t– мутность золя (латекса), которую можно измерить с помощью нефелометра, см — 1 ; l – длина волны падающего света, см; n₁, n₂ – коэффициенты преломления соответственно дисперсионной среды и дисперсной фазы,

. (2.2.114)

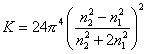
Уравнение (2.2.113) позволяет по измеренной мутности рассчитать радиус частиц, если система подчиняется закону Рэлея для рассеяния света, т.е. при r

Измерение мутности разбавленного белого золя проводят на нефелометре, а оптической плотности — на фотоколориметре. Иногда шкала фотоколориметра бывает отградуирована как в единицах мутности, так и в единицах оптической плотности.

Если радиус частиц больше l /20, то светорассеяние в таком золе не подчиняется уравнению Рэлея. Это выражается в том, что показатель степени при длине волны падающего света будет отличаться от 4.

Тогда используют эмпирическое уравнение Геллера

D = const l -a , (2.2.122)

или в логарифмической форме

lgD=lg (const) – a lgl . (2.2.123)

В уравнении (2.2.123) величина а обычно изменяется от 4 (рэлеевское рассеяние света) до 2 при r »l. Часто для белых золей используют параметр

где l_ср – среднее значение длин волн света, использованных для определения оптической плотности латекса.

Этот параметр зависит от показателя степени при длине волны использованного света a и после экспериментального определения последнего по углу зависимости, описываемой уравнением (2.2.123) находят по таблице величину Z и рассчитывают радиус частиц. Z лежит в пределах от 2 до 8.

Если Z 8 частицы уже видны в оптический микроскоп. Значения параметра Z и соответствующие ему показатели степени а при длине волны света приведены в табл. 2.1.

Рис. 2.18. Зависимость показателя степени при длине волны света в уравнении (2.2.122) от размера (радиуса) частиц в белых золях

Из табл. 2.1 видно, что постоянная а не может быть меньше 2,3 и больше 3,9.

В 1946 г. Геллер установил зависимость показателя степени в уравнении (2.2.123) для белых золей от размера частиц, экспериментально определяемого независимым методом. Калибровочная кривая Геллера, которая может быть использована для графического определения радиуса частиц, приведена на рис. 2.18. Для радиуса частиц от 50 до 100 нм калибровочная зависимость имеет линейный вид и может быть описана уравнением

a = 3,1 — 2,16×10 -2 (r -50). (2.2.125)

Это уравнение справедливо для а = 3,1¸2,0. Для других значений показателя степени а расчет надо проводить с использованием функции Z. Для подавляющего большинства латексов синтетических полимеров радиус частиц более 25 нм, поэтому уравнение Рэлея не может быть использовано. Размер частиц таких латексов можно определить с помощью метода Геллера по результатам определения показателя степени при длине волны в уравнении (2.2.122) с последующим использованием табл. 2.1, калибровочной кривой или уравнения (2.2.125).

Видео:Трёхполосник 2-я часть. Что за схема, как звучит?Скачать

Определение размеров частиц дисперсных систем турбидиметрическим методом. Константы, не зависящие от длины волны

Страницы работы

Фрагмент текста работы

Федеральное агентство по образованию Российской Федерации

Государственное образовательное учреждение высшего профессионального образования

Санкт-Петербургский Государственный Горный институт им. Г.В.Плеханова

Взаимосвязь показателя степени n в уравнении геллера и параметра z

(технический университет)

КАФЕДРА ОБЩЕЙ И ФИЗИЧЕСКОЙ ХИМИИ

Отчёт по лабораторной работе № 4.

По дисциплине: Физическая химия л

(наименование учебной дисциплины согласно учебному плану)

Тема: «Определение размеров частиц дисперсных систем турбидиметрическим методом»

Выполнил: студент гр. ОП-04 ______________ / /

ПРОВЕРИЛ:

Руководитель: доцент ______________ / /

(должность) (подпись) (Ф.И.О.)

Экспериментальное определение размеров частиц высокодисперсных систем.

Уравнение Рэлея может быть использовано для определения размеров частиц формы, близкой к сферической, если их радиус R не превышает 0,1l длины волны падающего света. Уравнение Рэлея определяет интенсивность рассеянного света от размера частиц, угла рассеяния и длины волны падающего света:

(1)

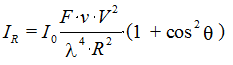
где I₀ – интенсивность падающего света, I_R – интенсивность рассеянного света, F – функция показателей преломления дисперсной и дисперсионной среды, равная

где n₁, n₀ – показатели преломления дисперсной и дисперсионных фаз соответственно, n — концентрация частиц в единице объема, V – объем частицы, l — длина волны падающего света, R – расстояние частицы от источника света (оптический путь), Q — угол рассеяния.

Из уравнения Рэлея радиус частицы равен:

(2)

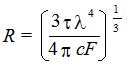
где с – концентрация взвешенных частиц, t — мутность системы, определяемая из уравнения (1), как I_s/I₀.

Необходимым условием использования уравнений (1) и (2) для дисперсных систем является отсутствие поглощения света, а также минимум вторичного светорассеяния. Поэтому уравнение Рэлея применимо только для «белых» золей, т.е., не поглощающих свет дисперсных систем при очень низких концентрациях дисперсной фазы.

Для дисперсных сред, неудовлетворяющих уравнению Рэлея используют турбидиметрические измерения. Турбидиметрические методы основаны на измерении интенсивности проходящего через дисперсную среду света. Рассеянный свет можно считать фиктивно поглощенным, и поэтому для проходящего света можно принять закон Бугера – Ламберта – Бера для определения кажущейся оптической плотности. Для дисперсных сред закон Бугера –Ламберта – Бера связывает мутность среды с кажущейся оптической плотности:

(3)

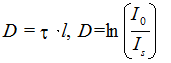
Мутность t = I_s/I0 , а отсюда и оптическая плотность D в соответствии с уравнениями (1) и (2) пропорциональна концентрации и квадрату объема частиц. Это позволяет определять размеры частиц и их концентрацию по кажущейся оптической плотности системы с помощью турбидиметрических измерений.

При увеличении размеров частиц закон Рэлея не выполняется, и интенсивность рассеянного света становится обратно пропорциональной длине волны в степени меньше чем четвертая. В общем случае для поглощающих золей степень при длине волны становится дробной, что делает невозможным использование уравнения Рэлея. Если размер (диаметр) взвешенных частиц составляет от 1/10 до 1/3 длины световой волны и показатели преломления частиц и среды не сильно различаются, то в случае турбидиметрических измерений можно пользоваться эмпирическим уравнением Геллера:

D = kλ — n и τ=k ’ λ — n (4)

где k и k’ – константы, не зависящие от длины волны.

Зависимость lgD от lg( в соответствии с уравнением (4) представляет собой прямую, тангенс угла наклона которой равен показателю степени n с минусом. Показатель степени связан с длиной волны и размером частиц эмпирическим соотношением:

которое табулировано для n 3 раствора (I) + 5 см 3 воды + 4 см 3 спирта

1 см 3 раствора (II) + 5 см 3 воды + 4 см 3 спирта

б) 1 см 3 раствора (I) + 2 см 3 воды + 3 см 3 спирта

1 см 3 раствора (II) + 2 см 3 воды + 3 см 3 спирта

с)1 см 3 раствора (I) + 1,5 см 3 воды + 3,5 см 3 спирта

1 см 3 раствора (II) + 1,5 см 3 воды + 3,5 см 3 спирта

— залить исследуемый золь в кювету с толщиной 1 см, залить воду