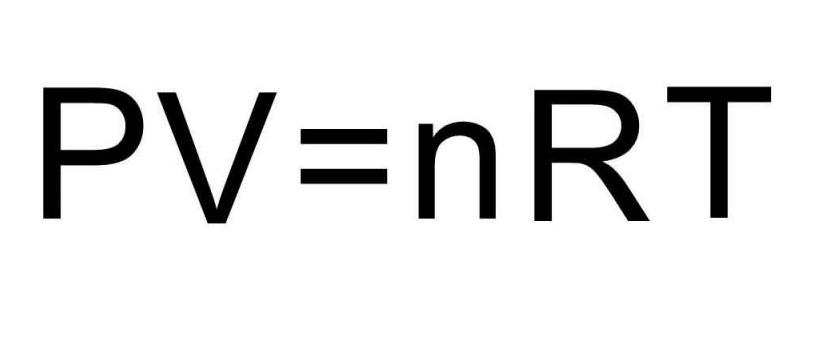Вывод уравнения внутренней энергии идеального газа

Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Формула внутренней энергии идеального газа. Изменение внутренней энергии газа: формула

Изучая поведение газов в физике, часто возникают задачи на определение запасенной в них энергии, которую теоретически можно использовать для совершения некоторой полезной работы. В данной статье рассмотрим вопрос, по каким формулам внутренняя энергия идеального газа может быть рассчитана.

Видео:Внутренняя энергия. 10 класс.Скачать

Понятие о газе идеальном

Четкое понимание концепции идеального газа важно при решении задач с системами, находящимися в этом агрегатном состоянии. Любой газ принимает форму и объем сосуда, в который его помещают, однако, не всякий газ является идеальным. Например, воздух можно считать смесью идеальных газов, в то же время водяной пар не является таковым. В чем же заключается принципиальная разница между реальными газами и их идеальной моделью?

Вам будет интересно: «Заклание» – это про необходимую жертву

Ответом на поставленный вопрос будут две следующие особенности:

• соотношение между кинетической и потенциальной энергией молекул и атомов, составляющих газ;
• соотношение между линейными размерами частиц газа и средним расстоянием между ними.

Газ считается идеальным только в том случае, когда средняя кинетическая энергия его частиц несоизмеримо больше энергии связи между ними. Разница между этими энергиями такова, что можно считать, что взаимодействие между частицами полностью отсутствует. Также для идеального газа характерно отсутствие размеров у его частиц, вернее эти размеры можно не учитывать, поскольку они намного меньше средних межчастичных расстояний.

Вам будет интересно: Московская лингвистическая школа: общая характеристика, основатель, представители

Хорошими эмпирическими критериями, позволяющими определить идеальность газовой системы, являются такие ее термодинамические характеристики, как температура и давление. Если первая больше 300 К, и второе меньше 1 атмосферы, то любой газ может полагаться идеальным.

Видео:Физика 10 класс (Урок№23 - Внутренняя энергия. Работа. Количество теплоты.)Скачать

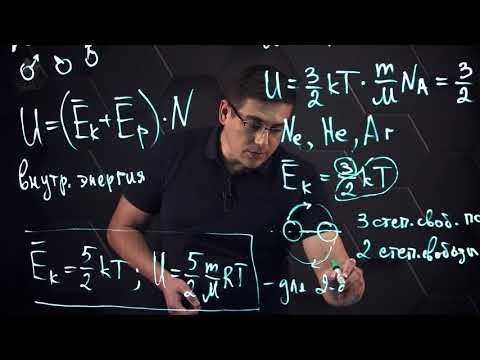
Что это внутренняя энергия газа?

Прежде чем записать формулу внутренней энергии газа идеального, необходимо познакомится с этой характеристикой ближе.

В термодинамике внутреннюю энергию, как правило, обозначают латинской буквой U. Определяется в общем случае она по следующей формуле:

Где H — энтальпия системы, P и V — давление и объем.

По своему физическому смыслу внутренняя энергия состоит из двух составляющих: кинетической и потенциальной. Первая связана с различного рода движением частиц системы, а вторая — с силовым взаимодействием между ними. Если применить это определение к концепции газа идеального, у которого отсутствует потенциальная энергия, то величина U при любом состоянии системы будет точно равна его кинетической энергии, то есть:

Видео:10 класс урок №44 Внутренняя энергия идеального газаСкачать

Вывод формулы внутренней энергии

Выше мы установили, что для ее определения у системы с идеальным газом необходимо рассчитать его кинетическую энергию. Из курса общей физики известно, что энергия частицы массой m, которая поступательно движется в некотором направлении со скоростью v, определяется по формуле:

Ее также можно применить для газовых частиц (атомов и молекул), однако, необходимо сделать некоторые замечания.

Во-первых, под скоростью v следует понимать некоторую среднюю величину. Дело в том, что газовые частицы движутся с разными скоростями согласно распределению Максвелла-Больцмана. Последнее позволяет определить среднюю скорость, которая с течением времени не изменяется, если отсутствуют внешние воздействия на систему.

Во-вторых, формула для Ek1 предполагает энергию на одну степень свободы. Газовые частицы могут двигаться во всех трех направлениях, а также вращаться в зависимости от их строения. Чтобы учесть величину степени свободы z, следует ее умножить на Ek1, то есть:

Кинетическая энергия всей системы Ek в N раз больше, чем Ek1z, где N — общее число газовых частиц. Тогда для U получаем:

Согласно этой формуле, изменение внутренней энергии газа возможно только в том случае, если поменять число частиц N в системе, либо их среднюю скорость v.

Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Внутренняя энергия и температура

Применяя положения молекулярно-кинетической теории идеального газа, можно получить следующую формулу связи между средней кинетической энергией одной частицы и абсолютной температурой:

Здесь kB — постоянная Больцмана. Подставляя это равенство в формулу для U, полученную в пункте выше, приходим к следующему выражению:

Данное выражение можно переписать через количество вещества n и газовую постоянную R в следующем виде:

В соответствии с этой формулой, изменение внутренней энергии газа возможно, если поменять его температуру. Величины U и T зависят друг от друга линейно, то есть график функции U(T) представляет собой прямую линию.

Видео:Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать

Как строение газовой частицы влияет на внутреннюю энергию системы?

Под строением частицы газа (молекулы) имеется в виду количество атомов, которое ее составляет. Оно играет определяющую роль при подстановке соответствующей степени свободы z в формулу для U. Если газ является одноатомным, формула внутренней энергии газа принимает такой вид:

Откуда взялась величина z=3? Ее появление связано всего с тремя степенями свободы, которыми обладает атом, поскольку он может двигаться только в одном из трех пространственных направлений.

Если рассматривается двухатомная молекула газа, то внутреннюю энергию следует вычислять по такой формуле:

Как видим, двухатомная молекула уже имеет 5 степеней свободы, 3 из которых являются поступательными и 2 вращательными (в соответствии с геометрией молекулы, она может вращаться вокруг двух взаимно перпендикулярных осей).

Наконец, если газ является трех- и более атомным, то справедливо следующее выражение для U:

Сложные молекулы имеют 3 поступательных и 3 вращательных степени свободы.

Видео:Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать

Пример задачи

Под поршнем находится одноатомный газ при давлении 1 атмосфера. В результате нагрева газ расширился так, что его объем увеличился от 2-х литров до 3-х. Как при этом изменилась внутренняя энергия газовой системы, если процесс расширения был изобарным.

Чтобы решить эту задачу, недостаточно приведенных в статье формул. Необходимо вспомнить об уравнении состояния идеального газа. Оно имеет вид, представленный ниже.

Поскольку поршень закрывает цилиндр с газом, то в процессе расширения количество вещества n остается постоянным. Во время изобарного процесса температура изменяется прямо пропорционально объему системы (закон Шарля). Это означает, что формула выше запишется так:

Тогда выражение для внутренней энергии одноатомного газа примет форму:

Подставляя в это равенство значения давления и изменения объема в единицах СИ, получаем ответ: ΔU ≈ 152 Дж.

Видео:Физика. Термодинамика: Внутренняя энергия идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

Внутренняя энергия и работа идеального газа

теория по физике 🧲 термодинамика

Числом степеней свободы механической системы называют количество независимых величин, с помощью которых может быть задано положение системы.

Внутренняя энергия идеального газа представляет собой сумму только кинетической энергии всех молекул, а потенциальной энергией взаимодействия можно пренебречь:

U = ∑ E k 0 = N E k 0 = m N A M . · i k T 2 . . = i 2 . . · m M . . R T = i 2 . . ν R T = i 2 . . p V

i — степень свободы. i = 3 для одноатомного (или идеального) газа, i = 5 для двухатомного газа, i = 6 для трехатомного газа и больше.

Видео:Внутренняя энергия. Практическая часть. 10 класс.Скачать

Изменение внутренней энергии идеального газа в изопроцессах

Δ U = 3 2 . . · m M . . R T = 3 2 . . ν R T = 3 2 . . ν R ( T 2 − T 1 )

Температура при изотермическом процессе — величина постоянная. Так как внутренняя энергия идеального газа постоянной массы в замкнутой системе зависит только от изменения температуры, то она тоже остается постоянной.

Δ U = 3 2 . . ν R ( T 2 − T 1 ) = 3 2 . . ( p V 2 − p V 1 ) = 3 2 . . p Δ V

Δ U = 3 2 . . ν R ( T 2 − T 1 ) = 3 2 . . ( p 2 V − p 1 V ) = 3 2 . . V Δ p

Δ U = 3 2 . . ν R ( T 2 − T 1 ) = 3 2 . . ( p 2 V 2 − p 1 V 1 )

Пример №1. На рисунке показан график циклического процесса, проведенного с идеальным газом. На каком из участков внутренняя энергия газа уменьшалась?

Внутренняя энергия газа меняется только при изменении температуры. Так как она прямо пропорциональная температуре, то уменьшается она тогда, когда уменьшается и температура. Температура падает на участке 3.

Видео:Урок 166. Предмет термодинамики. Внутренняя энергия телаСкачать

Работа идеального газа

Если газ, находящийся под поршнем, нагреть, то, расширяясь, он поднимет поршень, т.е. совершит механическую работу.

Механическая работа вычисляется по формуле:

Перемещение равно разности высот поршня в конечном и начальном положении:

Также известно, что сила равна произведению давления на площадь, на которое это давление оказывается. Учтем, что направление силы и перемещения совпадают. Поэтому косинус будет равен единице. Отсюда работа идеального газа равна произведению давления на площадь поршня:

Работа идеального газа

p — давление газа, S — площадь поршня

Работа, необходимая для поднятия поршня — полезная работа. Она всегда меньше затраченной работы, которая определяется изменением внутренней энергии идеального газа при изобарном расширении:

A ‘ = p ( V 2 − V 1 ) = p Δ V > 0

Внимание! Знак работы определяется только знаком косинуса угла между направлением силы, действующей на поршень, и перемещением этого поршня.

Работа идеального газа при изобарном сжатии:

A ‘ = p ( V 2 − V 1 ) = p Δ V 0

Работа идеального газа при нагревании газа:

A ‘ = ν R Δ T = ν R ( T 2 − T 1 ) = m M . . ν R Δ T

Внимание! В изохорном процессе работа, совершаемая газом, равна нулю, так как работа газа определяется изменением его объема. Если изменения нет, работы тоже нет.

Видео:Физика. 10 класс. Внутренняя энергия идеального газа. Термодинамическая работаСкачать

Геометрический смысл работы в термодинамике

В термодинамике для нахождения работы можно вычислить площадь фигуры под графиком в осях (p, V).

Примеры графических задач

Изохорное охлаждение и изобарное сжатие:

Изобарное расширение: A ‘ = p ( V 2 − V 1 )
Изобарное сжатие: A ‘ = p ( V 2 − V 1 )
Изохорное охлаждение:
Замкнутый цикл: 1–2: A ‘ = ( p 1 − p 3 ) ( V 2 − V 1 )
Произвольный процесс: A ‘ = p 1 + p 2 2 . . ( V 2 − V 1 )

Пример №2. На pV-диаграмме показаны два процесса, проведенные с одним и тем же количеством газообразного неона. Определите отношение работ A₂ к A₁ в этих процессах.

Неон — идеальный газ. Поэтому мы можем применять формулы, применяемые для нахождения работы идеального газа. Работа равна площади фигуры под графиком. С учетом того, что в обоих случаях изобарное расширение, получим:

A 2 = p ( V 2 − V 1 ) = 4 p ( 5 V − 3 V ) = 4 p 2 V = 8 p V

A 1 = p ( V 2 − V 1 ) = p ( 5 V − V ) = 4 p V

Видно, что работа, совершенная во втором процессе, вдвое больше работы, совершенной газом в первом процессе.

Идеальный одноатомный газ переходит из состояния 1 в состояние 2 (см. диаграмму). Масса газа не меняется. Как изменяются при этом следующие три величины: давление газа, его объём и внутренняя энергия?

Для каждой величины подберите соответствующий характер изменения:

3) не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

1. Определить по графику, как меняется давление.
2. Определить, как меняется объем.
3. Определить, отчего зависит внутренняя энергия газа, и как она меняется в данном процессе.

Решение

На графике идеальный одноатомный газ изотермически сжимают, так как температура остается неизменной, а давление увеличивается. При этом объем должен уменьшаться. Но внутренняя энергия идеального газа определяется его температурой. Так как температура постоянна, внутренняя энергия не изменяется.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Один моль аргона, находящийся в цилиндре при температуре T₁=600 K и давлении p₁=4⋅10 5 Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p₂=10 5 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?

Видео:Физика Внутренняя энергия идеального газаСкачать

Внутренняя энергия идеального газа — формулы и примеры вычислений

Видео:Урок 168. Задачи на вычисление внутренней энергииСкачать

Исторический экскурс

На середину XVII века приходится период расцвета экспериментальной физики. Во время опытов с заполненной ртутью стеклянной трубкой — прообразом барометра — Э. Торричелли в 1643 году обнаружил, что воздух имеет массу. Через девять лет в городе Магдебурге Отто фон Герике публично поставил эксперимент с медными полушариями, который наглядно продемонстрировал наличие атмосферного давления.

В 1662 году англичанин Р. Бойль установил, что при постоянной массе и температуре произведение давления газа на объём является величиной, которая не изменяется. Открытие стало одним из фундаментальных газовых законов, получившим имя Бойля-Мариотта.

В 1802 году французский академик Ж. Л. Гей-Люссак опубликовал статью, в которой сформулировал закон объёмов. По утверждению профессора химии, при постоянном давлении и массе между объёмом и температурой газа наблюдается прямо пропорциональная зависимость. При этом исследователь установил, что коэффициент изменения объёма одинаков для любой газовой среды.

В 30-х годах XIX столетия Гей-Люссак и офицер французской армии Николя Сади Карно независимо друг от друга объединили в одном уравнении законы Бойля-Мариотта и Шарля-Гей-Люссака. Однако математическому выражению, описывающему состояние газового тела, присвоили имя Б. Клапейрона, который в 1834 году подробно изложил идеи предшественников в мемуаре «О движущей силе огня». Во второй половине XIX века немецкий физик Р. Клаузиус опубликовал труды по теории термодинамики, где впервые ввел понятие «идеальный газ».

Значительным шагом в описании состояния идеального газа стал переход к универсальной газовой постоянной, которая обозначается физиками латинской буквой R. Первую математическую формулировку представил русский военный инженер И. П. Алымов в статьях, опубликованных в выпусках «Морского сборника» за 1861 и 1864 гг. Те же результаты получил Д. И. Менделеев в 1874 году.

Итогом работы великого русского химика стала формула идеального газа, которая в современной науке носит название уравнения Менделеева-Клапейрона:

P ∙ V = R ∙ T, где:

• P — давление газа.
• V — объём в молях.
• R — универсальная газовая постоянная.
• T — температура газовой среды.

Видео:Работа, совершаемая при термодинамических процессах. 10 класс.Скачать

Теоретическая формулировка

Элементарные частицы тела, обладая кинетической энергией, находятся в постоянном хаотическом движении. А также молекулы и атомы взаимодействуют между собой посредством электрических сил отталкивания и притяжения, что свидетельствует о наличии потенциальной энергии. Кроме того, энергией обладают электроны в атомах. Таким образом, тело наполнено силой, слагаемые которой имеют различную природу.

Компоненты внутренней энергии объекта, не подверженному внешнему воздействию:

• кинетическое движение частиц;
• потенциальное межмолекулярное взаимодействие;
• электронные силы;
• внутриядерная энергия.

При теоретическом изучении процессов термодинамики используется понятие «идеальный газ». Упрощённая модель газообразного тела, в отличие от реального газа, предполагает отсутствие гравитационного и электромагнитного взаимодействия между атомами вещества, а также не берётся во внимание энергия ядра. При этом движение молекул, которые представляются материальными точками, не имеющими объёма, ограничивается упругим соударением.

Теория термодинамики предлагает следующую формулировку: «В идеальном газе внутренняя энергия определяется суммарной кинетической энергией теплового движения составляющих его молекул». В Международной системе единиц СИ за единицу измерения энергии принят Джоуль.

В термодинамике главным свойством энергии является функция состояния системы в конкретный момент времени. Поэтому изменение энергии зависит от первоначальных и конечных параметров газового тела и происходит при совершении механической работы или путём теплопередачи. Если работа совершается самим газовым объектом, то внутренняя энергия уменьшается. В случае внешнего физического воздействия энергетический потенциал газового тела увеличивается.

Теплопередачей считается переход внутренней энергии без механического воздействия на газовую среду. Иногда этот процесс называют теплообменом. Существуют следующие разновидности явления:

• Теплопроводность.
• Конвекция.
• Тепловое излучение.

Теплопроводность веществ

При нахождении тела в области повышенной температуры, например, под пламенем горелки или в горячей воде, атомы начинают совершать интенсивные колебательные движения. Тем самым увеличивается кинетическая энергия соседних частиц и происходит постепенная передача теплоты от участка к участку. Таким образом, теплопроводностью называется перенос энергии от тёплых фрагментов объекта к холодным посредством теплового движения частиц среды.

Лучшими тепловыми проводниками являются металлы. Меньшую теплопроводность имеют жидкости, а хуже всего передают тепло газы. Предметы из плотного материала проводят тепло лучше, чем тела из пористого вещества.

Явление конвекции

Если в газообразную среду поместить горячий предмет, то нагретая субстанция устремится вверх. Освободившееся пространство заполнит газ с меньшей температурой. Аналогичное явление наблюдается в жидкостях.

Конвекцией называется перемещение внутренней энергии в процессе циркуляции газовых или жидкостных потоков, приводящей к перемешиванию вещества. За счёт конвекции, например, происходит обогрев помещений с помощью отопительных приборов. Перемещение воздушных масс в атмосфере также основано на принципах конвекции.

Тепловое излучение

Как известно, атомы состоят из заряженных положительно протонов, вокруг которых вращаются электроны, имеющие отрицательный заряд. Хаотическое движение элементарных частиц порождает электрические поля. Принято считать, что тепловое излучение является проявлением электромагнитных волн, которые возникают в результате теплового колебания атомов.

Тепловое излучение, способное распространяться в любом веществе и вакууме, испускает каждое тело. Влияние данного явления испытывает человек, который решил погреться под солнечными лучами. Наглядно увидеть тепловое излучение позволяют приборы ночного видения.

Видео:Внутренняя энергия | Физика 10 класс #38 | ИнфоурокСкачать

Математическое выражение

Согласно теоретическому определению идеального газа, внутренний потенциал слагается из кинетических энергий всех частиц. На языке математике это выражается следующей формулой:

где: U — внутренняя энергия тела;

N — количество элементарных частиц;

Ek — кинетическая энергия одной молекулы.

Число молекул определяется по формуле:

где: ν — количество вещества;

NA — постоянная Авогадро, константа, равная 6,02 ∙ 10 23 моль -1

Энергия движения молекулы вычисляется из уравнения:

где: i — количество степеней свободы, которые полностью определяют пространственное положение системы;

k — постоянная Больцмана, значение которой равно 1,38 ∙ 10 -23 Дж/К;

T — температура объекта измеряется по абсолютной шкале Кельвина.

Постановка уравнений количества молекул и кинетической энергии в формулу даёт следующее выражение:

U = (i/2) ∙ ν ∙ k ∙ NA ∙ T.

Произведение постоянных величин (k ∙ NA) называется универсальной газовой постоянной R, которая равна 8,31 Дж/(моль ∙ К). Тогда формула изменения внутренней энергии газа принимает окончательный вид:

где ∆T — разница между начальной и конечной температурой газового тела.

Полная кинетическая энергия складывается из поступательного и вращательного движения частиц. В одноатомном газе отсутствует вращательное движение молекул. В многоатомном газе необходимо принимать во внимание вращение молекул. Соотношение поступательного и вращательного моментов учитывается законом распределения энергии по степеням свободы. Это правило утверждает, что на одну степень свободы i приходится ½ ∙ (k ∙ T) всей энергии.

Таблица 1. Зависимость числа степеней свободы от количества атомов в молекуле.

Видео:мкт РАБОТА В ТЕРМОДИНАМИКЕ внутренняя энергия идеального газаСкачать

Решение практической задачи

Задача.

Термоизолированный баллон, заполненный водородом, чья молярная масса равна 2,00 г/моль, движется со скоростью 250 м/с. Как изменится газовая температура при мгновенной остановке сосуда, теплоёмкостью которого можно пренебречь?

Решение.

Полная энергия газового тела W складывается из энергии водорода U и кинетической энергии движущегося тела E, или W = U + E. При движении сосуда:

W₁ = U₁ + E₁ = [(i/2) ∙ ν ∙ R ∙ T₁] + [mv²/2] = [(5/2) ∙ (m/M) ∙ R ∙ T₁] + [mv²/2],

где i = 5, так как молекула водорода состоит из двух атомов;

ν — является частным от деления массы газа m на молярную массу водорода M;

R — универсальная газовая постоянная;

T₁ — начальная температура газа;

v — скорость движения.

После остановки сосуда, когда E₂ = 0, полная энергия равна:

W₂ = U₂+ E₂ = [(i/2) ∙ ν ∙ R ∙ T₂] = [(5/2) ∙ (m/M) ∙ R ∙ T₂], где T₂ — конечная температура газа.

Поскольку в термоизолированном баллоне не происходит теплообмена между окружающей средой и газом, то можно записать:

W₁ = W₂, или [(5/2) ∙ (m/M) ∙ R ∙ T₁] + [mv²/2] = [(5/2) ∙ (m/M) ∙ R ∙ T₂].

Из полученного уравнения можно найти разность температур:

∆T = (v² ∙ M)/(5 ∙ R), или [(250)²∙ 2,0 ∙ 10ˉ³]/[5 ∙ 8,31] = 3 K.

Ответ. При мгновенной остановке баллона с водородом температура газа повысится на 3 градуса по шкале Кельвина.

Законы термодинамики изучаются в старших классах общеобразовательной школы. Понимание смысла теории идеального газа поможет на выпускном экзамене, а умение решать задачи облегчит применение знаний на практике.

🔍 Видео

Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

Температура. Вывод уравнения состояния идеального газа на основе МКТСкачать

Физика 10 класс (Урок№18 - Основное уравнение МКТ.)Скачать