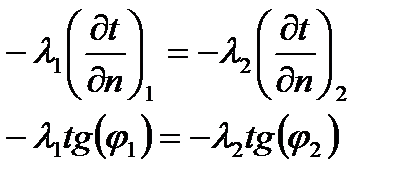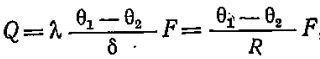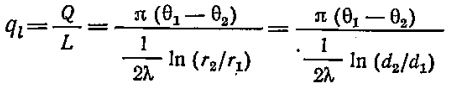При построении математической модели распространения тепла в стержне сделаем следующие предположения:
1) стержень сделан из однородного проводящего материала с плотностью ρ;
2) боковая поверхность стержня теплоизолирована, то есть тепло может распространяться только вдоль оси ОХ;
3) стержень тонкий — это значит, что температура во всех точках любого поперечного сечения стержня одна и та же.
Рассмотрим часть стержня на отрезке [х, х + ∆х] (см. рис. 6) и воспользуемся законом сохранения количества тепла:
Общее количество тепла на отрезке [х, х + ∆х] = полному количеству тепла, прошедшему через границы + полное количество тепла, образованного внутренними источниками.
Общее количество тепла, которое необходимо сообщить участку стержня, чтобы повысить его температуру на ∆U, вычисляется по формуле: ∆Q= CρS∆x∆U, где С — удельная теплоемкость материала ( = количеству тепла, которое нужно сообщить 1 кг вещества, чтобы поднять его температуру на 1°), S — площадь поперечного сечения.
Количество тепла, прошедшее через левый конец участка стержня за время ∆t (тепловой поток) вычисляется по формуле: Q1 = -kSUx(x, t)∆t, где k — коэффициент теплопроводности материала ( = количеству тепла, протекающего в секунду через стержень единичной длины и единичной площади поперечного сечения при разности температур на противоположных концах, равной 1°). В этой формуле особого пояснения требует знак минус. Дело в том, что поток считается положительным, если он направлен в сторону увеличения х, а это, в свою очередь, означает, что слева от точки х температура больше, чем справа, то есть Ux CpS∆x∆U = kSUx(x + ∆х, t) ∆t — kSUx(x, t)∆t.
Если это равенство поделить на S∆x∆t и устремить ∆х и ∆t к нулю, то будем иметь:
Отсюда уравнение теплопроводности имеет вид
Ut = a 2 Uxx,
где 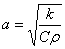
В случае, когда внутри стержня имеются источники тепла, непрерывно распределенные с плотностью q(x,t), получится неоднородное уравнение теплопроводности
Начальные условия и граничные условия.
Для уравнения теплопроводности задается только одно начальное условие U|t=0 = φ(х) (или в другой записи U(x,0) = φ(х)) и физически оно означает, что начальное распределение температуры стержня имеет вид φ(х). Для уравнений теплопроводности на плоскости или в пространстве начальное условие имеет такой же вид, только функция φ будет зависеть, соответственно, от двух или трех переменных.
Граничные условия в случае уравнения теплопроводности имеют такой же вид, как и для волнового уравнения, но физический смысл их уже иной. Условия первого рода (5) означают, что на концах стержня задана температура. Если она не изменяется со временем, то g1(t) ≡ Т1 и g2(t) ≡ Т2, где Т1 и Т2 — постоянные. Если концы поддерживаются все время при нулевой температуре, то Т1= Т2 = 0 и условия будут однородными. Граничные условия второго рода (6) определяют тепловой поток на концах стержня. В частности, если g1(t) = g2(t) = 0, то условия становятся однородными. Физически они означают, что через концы не происходит теплообмен с внешней средой (эти условия еще называют условиями теплоизоляции концов). Наконец, граничные условия третьего рода (7) соответствуют случаю, когда через концы стержня происходит теплообмен с окружающей средой по закону Ньютона (напомним, что при выводе уравнения теплопроводности мы считали боковую поверхность теплоизолированной). Правда, в случае уравнения теплопроводности условия (7) записываются немного по-другому:
Физический закон теплообмена со средой (закон Ньютона) состоит в том, что поток тепла через единицу поверхности в единицу времени пропорционален разности температур тела и окружающей среды. Таким образом, для левого конца стержня он равен Здесь h1 > 0 — коэффициент теплообмена с окружающей средой, g1(t) — температура окружающей среды на левом конце. Знак минус поставлен в формуле по той же причине, что и при выводе уравнения теплопроводности. С другой стороны, в силу теплопроводности материала поток тепла через этот же конец равен Применив закон сохранения количества тепла, получим:
Аналогично получается условие (14) на правом конце стержня, только постоянная λ2 может быть другой, так как, вообще говоря, среды, окружающие левый и правый конец, бывают разные.
Граничные условия (14) являются более общими по сравнению с условиями первого и второго рода. Если предположить, что через какой-либо конец не происходит теплообмена со средой (то есть коэффициент теплообмена равен нулю), то получится условие второго рода. В другом случае предположим, что коэффициент теплообмена, например h1, очень большой.
Перепишем условие (14) при х = 0 в виде и устремим . В результате будем иметь условие первого рода:
Аналогично формулируются граничные условия и для большего числа переменных. Для задачи о распространении тепла в плоской пластине условие означает, что температура на ее краях поддерживается нулевой. Точно так же, условия и внешне очень похожи, но в первом случае оно означает, что рассматривается плоская пластина и края ее теплоизолированы, а во втором случае оно означает, что рассматривается задача о распространении тепла в теле и поверхность его теплоизолирована.
Решение первой начально-краевой задачи для уравнения теплопроводности.
Рассмотрим однородную первую начально-краевую задачу для уравнения теплопроводности:
Найти решение уравнения
удолетворяющее граничным условиям
и начальному условию
Решим эту задачу методом Фурье.
Шаг 1. Будем искать решения уравнения (15) в виде U(x,t) = X(x)T(t).
Найдем частные производные:
Подставим эти производные в уравнение и разделим переменные:
По основной лемме получим
Теперь можно решить каждое из этих обыкновенных дифференциальных уравнений. Обратим внимание на то, что используя граничные условия (16), можно искать не общее решение уравнения б), а частные решения, удолетворяющие соответствующим граничным условиям:
Шаг 2. Решим задачу Штурма-Лиувилля
Эта задача совпадает с задачей Штурма-Лиувилля, рассмотренной в лекции 3. Напомним, что собственные значения и собственные функции этой задачи существуют только при λ>0.
Собственные значения равны
Собственные функции равны (См. решение задачи)
Шаг 3. Подставим собственные значения в уравнение а) и решим его:
Шаг 4. Выпишем частные решения уравнения (15):
В силу линейности и однородности уравнения (15) их линейная комбинация
Шаг 5. Определим коэффициенты An в (19), используя начальное условие (17):
Приходим к тому, что начальная функция φ(x) разлагается в ряд Фурье по собственным функциям задачи Штурма-Лиувилля. По теореме Стеклова такое разложение возможно для функций, удовлетворяющих граничным условиям и имеющих непрерывные производные второго порядка. Коэффициенты Фурье находятся по формулам
Вычислив эти коэффициенты для конкретной начальной функции φ(x) и подставив их значения в формулу (19), мы тем самым получим решение задачи (15), (16), (17).
Замечание. Используя формулу (19), можно также, как в лекции 3, получить решение первой начально-краевой задачи для уравнения Ut = a 2 Uxx. Оно будет иметь вид
где
Видео:Вывод уравнения теплопроводностиСкачать

Вопрос 31. Теплопроводность. Закон Фурье. Коэффициент теплопроводности.
Теплопроводность — процесс передачи теплоты путем непосредственного соприкосновения тел, имеющих различную температуру. При этом процесс теплообмена происходит за счет передачи энергии микродвижения одних частиц другим.
Тепловой поток 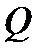
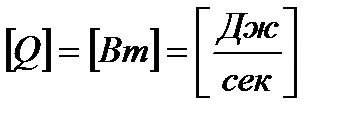
Закон Фурье: тепловой поток пропорционален градиенту температуры и площади, то есть 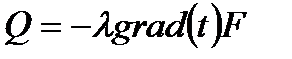
Плотность теплового потока 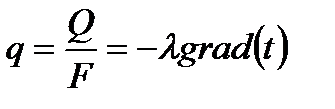
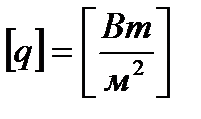
Коэффициент теплопроводности 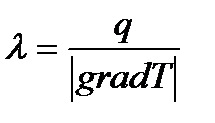
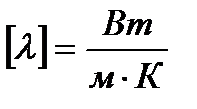
_____________________________________________________________________
Вопрос 32. Дифференциальное уравнение теплопроводности. Условия однозначности.
Условности:
1. Теплофизические свойства системы: 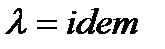
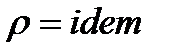

2. Микрочастицы тела неподвижны.
3. Внутренние источники теплоты распределены в теле равномерно.
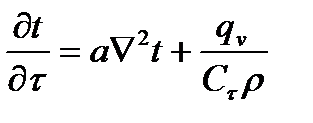
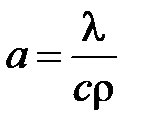
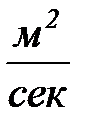
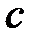
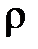

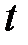

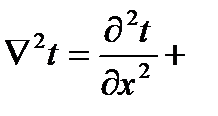
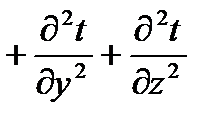
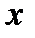
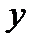
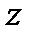
Условия однозначности – математическое описание частных особенностей рассматриваемого процесса.
Решая уравнение 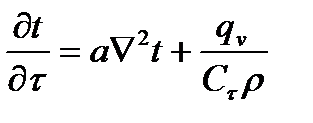
Условия однозначности:
1. Геометрические условия (характеризуют форму, размеры и положение тела в пространстве):
a. Форма тела (плоское, цилиндрическое сферическое тело)
b. Ограниченное тело.
c. Неограниченное тело.
2. Физические условия (определяют физические свойства тела и среды)
a. Характер изменения физических параметров:
i. Характер изменения 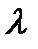
ii. Характер изменения 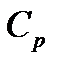
iii. Характер изменения 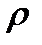
iv. Характер изменения 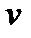
3. Временные условия (дают представление о распределении температуры в исследуемом теле в начальный момент времени):
a. 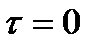
i. 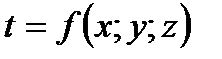
ii. 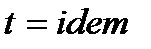
b. 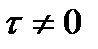
4. Граничные условия (определяют особенности взаимодействия на границе изучаемого тела с окружающими телами (средой)):
a. Граничные условия первого рода – закон изменения температуры на границе тела:
i. 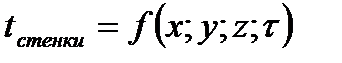
ii. 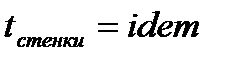
b. Граничные условия второго рода – закон изменения температурного потока в стенке тела:
i. 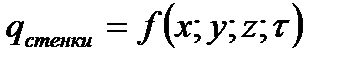
ii. 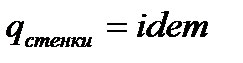
c. Граничные условия третьего рода:
i. Закон изменения температуры окружающей среды.
ii. Закон, по которому идёт теплообмен тела с окружающей средой, 
d. Граничные условия четвёртого рода, 
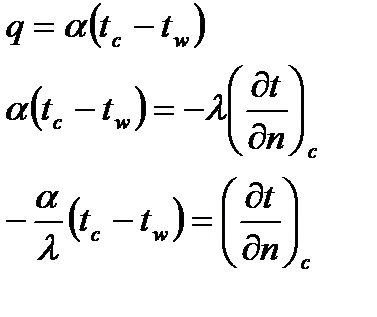


________________________________________________________
Билет 33. Теплопроводность через однослойные и многослойные плоские стенки.
Теплопроводность – процесс передачи теплоты соприкасающимися, беспорядочно движущимися структурными частицами вещества
В основу теории теплопроводности положен закон Фурье – тепловой поток прямо пропорционален температурному градиенту и площади поверхности тела. Закон Фурье для плоской однослойной стенки
Плотность теплового потока – отношение теплового потока к площади поверхности теплопроводности. Для плоской стенки:
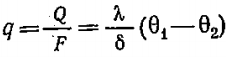

Коэффициент теплопроводности λ характеризует способность тел проводить теплоту.
Плотность теплового потока для стенки, состоящей из n слоёв:
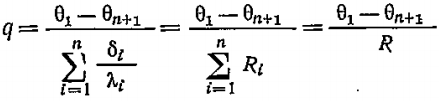
где R – термическое сопротивление многослойной стенки
Многослойную стенку можно заменить эквивалентной однослойной, толщина которой равна толщине многослойной стенки
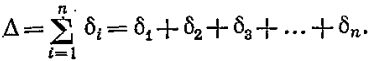
Тогда плотность теплового потока 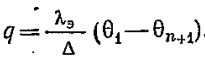
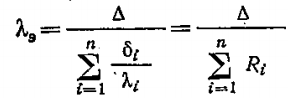
_____________________________________________________________________
Вопрос 34. Теплопроводность через однослойные и многослойные цилиндрические стенки
Тепловой поток для цилиндрической однослойной стенки:
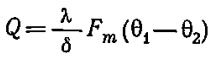
где Fm — расчётная поверхность теплопроводности,
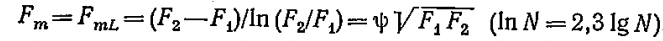
где.
δ – толщина стенки, δ=r2 – r1
F1, F2 – площади внутренней и наружной поверхностей трубы, [м 2 ]
ψ – коэффициент, характеризующий отношение средней логарифмической FmL к средней геометрической 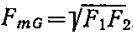
Линейная плотность теплового потока (тепловой поток, отнесённый к единице длины трубы) однослойной стенки определяется по формуле:
Тепловой поток для многослойной цилиндрической стенки:
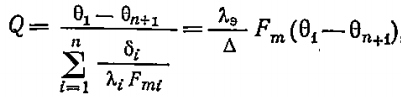
Где
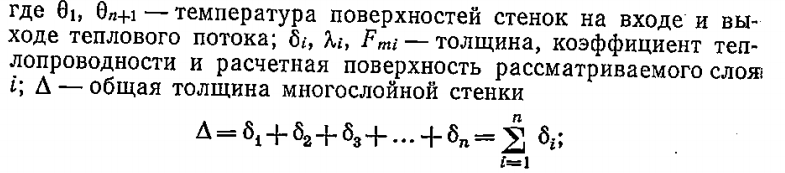
Fm – расчётная поверхность теплопроводности стенки;
λэ – эквивалентный коэффициент теплопроводности многослойной стенки
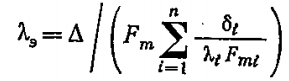
Линейная плотность теплового потока для многослойной стенки трубы
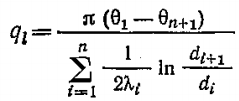
_____________________________________________________________________
Вопрос 35. Теплоотдача. Уравнение Ньютона. Коэффициент теплоотдачи.
Теплоотдача — конвективный теплообмен между жидкостью и поверхностью твёрдого тела (совместный перенос теплоты конвекцией и теплопроводностью).
Теплоотдачу рассчитывают по формуле Ньютона-Рихмана:
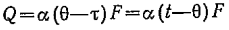
и плотность теплового потока
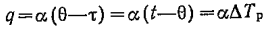

Коэффициент теплоотдачи зависит от: природы возникновения движения жидкости у поверхности теплообмена, режима движения жидкости, физических свойств жидкости, формы, размеров, положения в пространстве и состояния поверхности теплообмена.
____________________________________________________________________
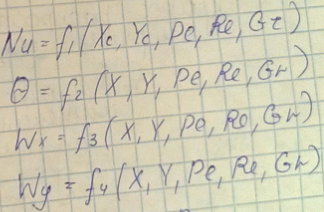
Число Нуссельта, или критерий теплоотдачи, характеризует соотношение тепловых потоков, передаваемых конвекцией и теплопроводностью по нормали через пристенный слой.
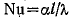
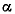
l – определяющий линейный размер, [м]
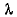
Число Рейнольдса – критерий гидродинамического подобия, характеризуется соотношением сил инерции и молекулярного трения (вязкости)
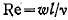
w – средняя (линейная) скорость жидкости, определяется отношением объемного расхода к площади поперечного сечения потока, [м/с], 
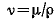
По числовому значению Re судят о режиме течения жидкости:
Re =10^4 – развитый турбулентный
2320 2 К 4 ], ε – степень черноты наружной поверхности опытной трубы, F – площадь наружной поверхности опытной трубы.
Тепловой поток, передаваемый от опытной трубы в окружающую среду путем конвекции, равен
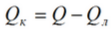
а опытное значение коэффициента теплоотдачи составляет
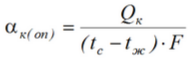
Определив при средней температуре пограничного слоя tm теплофизические свойства сухого воздуха λ; ν; β; Pr (находятся значения числа Грасгофа)

В зависимости от значения комплекса (GrPr) подбирается коэффициент C и показатель степени n в уравнении подобия конвективного теплообмена и определяются число Нуссельта
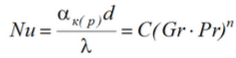
и расчетное значение коэффициента теплоотдачи
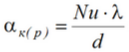
_____________________________________________________________________
Вопрос 38. Последовательность расчетов конвективного теплообмена в условиях вынужденной конвекции.
Рассчитаем конвективный теплообмен на примере лабораторной работы
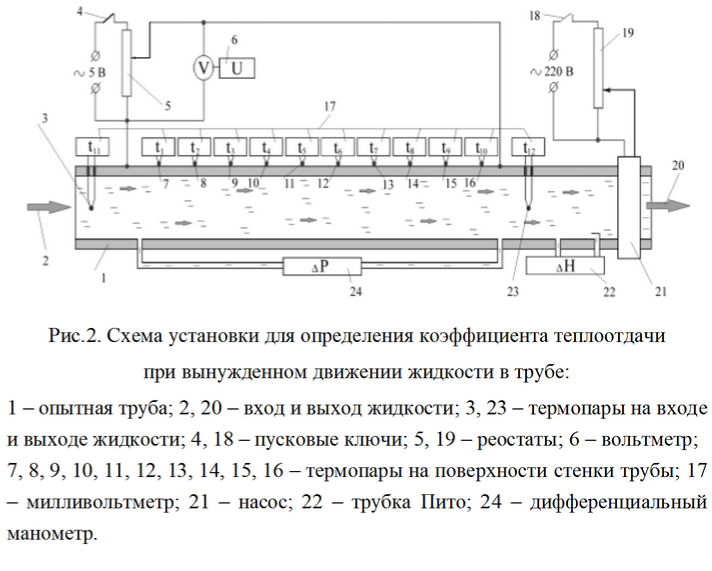
Дано: напряжение U [В]
Динамический напор жидкости ΔH [кГ/м 2 ]
Температура стенки трубы t1 [°С] (10 измерений)
Температура жидкости на входе в трубу t11 [°C]
Температура жидкости на выходе из трубы t12 [°С]
Рассчитаем коэффициент теплоотдачи
Обработка опытных данных начинается с определения средней темпе-ратуры поверхности стенки трубы tс:
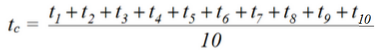
Средняя температура потока воды в трубе:
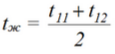
При средней температуре потока по таблице определяются теплофизические свойства воды: ρ; сp; λ; v.
Число Прандтля при средней температуре потока (10):
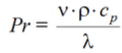
Скорость движения воды в трубе:
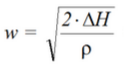
При движении жидкость нагревается на:
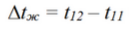
Количество теплоты в единицу времени, которое получает поток жид-кости от горячей поверхности стенки трубы:
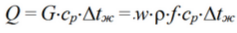
Плотность теплового потока от стенки трубы к потоку жидкости:
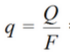
Опытное значение среднего коэффициента теплоотдачи:
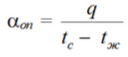
Число Рейнольдса (8) для потока жидкости в трубе:
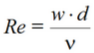
В зависимости от полученного значения определяется выражение для поиска числу Нуссельта.
Теоретическое значение среднего коэффициента теплоотдачи вычисляется из определения критерия Нуссельта
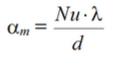
_____________________________________________________________________
Видео:Интуитивное понимание формулы теплопроводности (часть 11) | Термодинамика | ФизикаСкачать

Закон Фурье – основной закон теплопроводности.
В 1807 году французский ученый Фурье доказал экспериментально, что во всякой точке тела (вещества) в процессе теплопроводности присуща однозначная взаимосвязь между тепловым потоком и градиентом температуры:
,
где Q – тепловой поток, выражается в Вт;
grad(T) – градиент температурного поля (совокупности числовых значений температуры в разнообразных местах системы в выбранный момент времени), единицы измерения К/м;
S – площадь поверхности теплообмена, м 2 ;
Градиент температуры получится характеризовать в виде векторной суммы составляющих по осям декартовых координат:
,
где i, j, k – ортогональные между собой единичные векторы, нацеленные по координатным осям.
Значит, данный закон устанавливает величину теплового потока при переносе тепла посредством теплопроводности.
Закон Фурье для поверхностной плотности теплового потока принимает вид:
.
Знак « минус» обозначает, что векторы теплового потока и градиента температуры разнонаправленные. Следует понимать, что теплота передается в направлении спада температуры.
И все же не лишним будет указать, что закон Фурье не принимает в расчет инерционность процесса теплопроводности, иначе говоря, в представленной модели колебание температуры в любой точке мгновенно распространяется на всё тело. Закон Фурье некорректно применять для характеристики высокочастотных процессов таких как, к примеру, распространение ультразвука, ударной волны.
📹 Видео
Метод Фурье для неоднородного уравнения теплопроводностиСкачать

Л1 - Теплопроводность. Закон Фурье.Скачать

Демидович №4450: вывод уравнения теплопроводностиСкачать

Уравнение в частных производных Уравнение теплопроводностиСкачать

8.1 Решение уравнения теплопроводности на отрезкеСкачать

Закон и уравнение теплопроводностиСкачать

8.2 Теплопроводность на отрезке. Сложные задачи.Скачать

6-1. Уравнение теплопроводностиСкачать

Семинар по УМФ, метод Фурье для уравнения теплопроводности на отрезке, 27.04.2020Скачать

Уравнение колебаний струны. Метод разделения переменных. Метод ФурьеСкачать

Метод Фурье для уравнения теплопроводности (диффузии)Скачать

Лекция №1.1 Явная и неявная схемы для уравнения теплопроводностиСкачать

ЛиНУрФ. Лекция. 05.11.2020Скачать

Горицкий А. Ю. - Уравнения математической физики. Часть 2 - Уравнение теплопроводностиСкачать

Решение первой краевой задачи для неоднородного уравнения теплопроводности.Скачать

Передача тепла теплопроводностьюСкачать

УМФ, 22.12, вывод уравнения колебаний струныСкачать