Вывод уравнения смолуховского для определения концентрации частиц при быстрой коагуляции (8 видео)

Содержание

3.5.1. Теория быстрой коагуляции
Кинетика коагуляции коллоидов
Теория быстрой перекинетической коагуляции по Смолуховскому
Лако-красочные материалы — производство
Технологии и оборудование для изготовления красок, ЛКМ
КИНЕТИКА КОАГУЛЯЦИИ
📽️ Видео

Видео:Органика. Решение задачи на определение состава вещества по продуктам его сгорания.Скачать

3.5.1. Теория быстрой коагуляции

Поскольку, как говорилось выше, при быстрой коагуляции любое столкновение оказывается эффективным, то разработка теории быстрой коагуляции оказалась более простой задачей и именно такая теория была разработана М. Смолуховским в 1916 г.

При разработке своей теории он исходил из следующих предпосылок:

1) частицы дисперсной фазы сферические, а сами дисперсные системы являются монодисперсными, т.е. содержат частички одного размера;

2) скорость коагуляции определяется тремя факторами:

– радиусом сферы сил притяжения частиц;

– интенсивностью броуновского движения, которая определяет число столкновений в единицу времени и характеризуется коэффициентом диффузии D;

3) между частицами существуют только силы притяжения.

Последняя предпосылка означает, что в какой-то момент времени, который можно обозначить как t₀, внезапно и полностью исчезают силы, приводившие к отталкиванию частиц при их сближении. После этого времени любое столкновение частиц обязательно приведет к их агрегированию.

Смолуховский предложил рассматривать процесс коагуляции как попарное слипание частиц, чем формально уподобил процесс коагуляции химической реакции второго порядка. Считается, что вероятность одновременного столкновения трех частиц столь мала, что такие столкновения можно не учитывать.

Очевидно, что вначале будут образовываться агрегаты частиц, состоящие из двух первичных, затем первичная частица может объединяться с агрегатом из двух первичных частиц и образуется новый агрегат, состоящий из трех первичных частиц. Затем к нему присоединится еще одна частица и будет сформирован агрегат из четырех частиц и т.д. Назовем число частиц в агрегате порядком агрегата и будем считать, что при коагуляции последовательно будут сформированы агрегаты второго n₂, третьего n₃, четвертого n₄, пятого n₅ и т.д. порядков. В любой момент времени после начала коагуляции в дисперсной системе будет присутствовать набор агрегатов частиц, так что частичная концентрация будет определяться суммой всех агрегатов:

. (2.3.137)

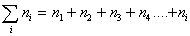
Выражая скорость коагуляции через уменьшение числа частиц в единице объема за единицу времени и учитывая, что общее число частиц может только уменьшаться, записываем

v = – dn/dt = kn 2 , (2.3.138)

где v – скорость коагуляции, k – постоянная скорости коагуляции, n – частичная концентрация (частиц/м 3 ).

Выяснение физического смысла постоянной скорости коагуляции проводится при рассмотрении диффузионного механизма сближения частиц.

Вначале решают задачу диффузионного сближения произвольной частицы с некоторой закрепленной в пространстве центральной частицей. Столкновение этой неподвижной частицы с другой происходит каждый раз, когда частицы сближаются на расстояние, равное их двойному радиусу(R = 2r). Таким образом, рассматривается диффузия точечных частиц к сфере радиуса R. При этом концентрация единичных (первичных) частиц на поверхности такой сферы равна нулю, поскольку на этой поверхности частицы образуют агрегаты.

Распределение частичной концентрации в дисперсной системе находят решением дифференциального уравнения диффузии (второго закона Фика)

, (2.3.139)

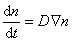
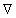
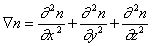
где – оператор Лапласа,

. (2.3.140)

В операторе Лапласа x, y, z характеризуют координаты точечной частицы относительно центра сферы радиуса R. Считается, что в начальный момент распределение частиц в объеме дисперсной системы можно принять равномерным, поэтому их концентрация относительно центра сферы определяется исключительно расстоянием до начала координат. Обозначим это расстояние h, тогда от полярных координат можно перейти к линейным и закон Фика в этом случае приобретает вид

, (2.3.141)

. (2.3.142)

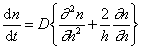
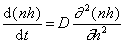
Граничные условия интегрирования уравнения (2.3.142) вытекают из соображений, что при t = 0 n = n₀ , если h > R, а при t > 0 n = 0 , если h = R.

Решение уравнения (2.3.139) при граничных условиях имеет вид

. (2.3.143)

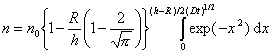
В стационарном процессе частичная концентрация n на расстоянии h не зависит от времени коагуляции, поэтому вторым членом в уравнении (2.3.143) можно пренебречь. Тогда уравнение (2.3.143) приводят к виду

В стационарном процессе поток частиц к сфере радиуса R, т.е. число всех частиц, которые пересекают поверхность этой сферы за 1 с. согласно первому закону Фика будет

, (2.3.145)

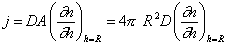
где А – площадь поверхности сферы.

Производную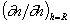 находят дифференцированием уравнения (2.3.144)

. (2.3.146)

Следовательно для диффузионного потока

Поскольку в реальных условиях ни одну из частиц невозможно сделать неподвижной, то и центральная частица перемещается в пространстве подобно диффундирующим к ней частицам. Поэтому необходимо рассматривать не движение диффундирующих частиц к некоторой неподвижной центральной частице, а относительное движение двух подвижных частиц.

Поскольку частицы перемещаются независимо друг от друга, то постоянная диффузии будет складываться из постоянных диффузии различных частиц, т.е.

Если частицы имеют одинаковый размер, то

Доказательство справедливости уравнений (2.3.148) и (2.3.149) проводят при рассмотрении относительного среднего сдвига частиц. Из теории броуновского движения известно, что

, (2.3.150)

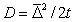
где 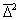— средний квадратичный сдвиг частицы.

Относительное смещение частиц будет

. (2.3.151)

. (2.3.152)

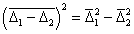
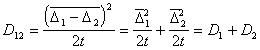
Для одинаковых частиц

. (2.3.153)

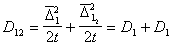
Для потока j частиц через сферу радиуса R, движущуюся вместе с одной из них, подставляя вместо D₁₂ =2 D, получаем

Поток j выражает скорость агрегирования по отношению к одной частице, для всех n₀ частиц в 1 м 3 она будет в n₀ раз больше, следовательно,

(2.3.155)

, (2.3.156)

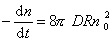
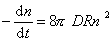
так как уравнение (2.3.155) справедливо для любой концентрации частиц в любой момент времени от начала коагуляции.

Таким образом, постоянная скорости коагуляции имеет физический смысл

Интегрирование уравнения (2.3.156) проводим в пределах от 0 до t и, соответственно, от n₀ до n. В результате интегрирования получаем

. (2.3.158)

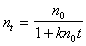
Это уравнение может быть использовано для расчета кинетической кривой коагуляции, однако экспериментальное определение постоянной скорости коагуляции встречает определенные трудности. В процессе коагуляции в результате слипания частиц происходит изменение их размера и, следовательно, коэффициента диффузии и радиуса сферы сил притяжения. При этом постоянная скорости коагуляции оказывается связанной с двумя неопределенными величинами. Поэтому кинетическое уравнение приводят к виду, не содержащему постоянной скорости коагуляции.

Прием, который применил Смолуховский, заключается в определении времени половинной коагуляции, когда

, (2.3.160)

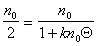
где Q – время половинной коагуляции, определяемое по времени, в течение которого начальная частичная концентрация изменится в два раза.

(2.3.161)

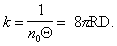
Подставляя значение постоянной скорости коагуляции из уравнения (2.3.161) в уравнение (2.3.158), получаем

. (2.3.162)

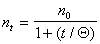
Определение постоянной скорости коагуляции можно проводить графическим методом после построения графика в координатах линейной формы уравнения Смолуховского

. (2.3.163)

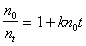
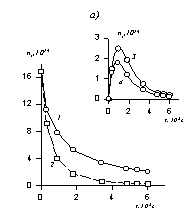
В соответствии с этим уравнением постоянную скорости коагуляции можно определить по тангенсу угла наклона, если известна величина начальной частичной концентрации n₀. Пример такой зависимости приведен на рис. 2.25.

В процессе коагуляции в результате слипания частиц происходит изменение их размера и, следовательно, коэффициент диффузии и радиуса сферы сил притяжения. При этом постоянная скорости коагуляции оказывается связанной с двумя неопределенными величинами. Поэтому кинетическое уравнение приводят к виду, не содержащему постоянной скорости коагуляции.

Для расчета концентрации агрегатов частиц любого порядка была получена формула

, (2.3.164)

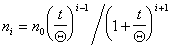
где i – порядок, т.е. число соединившихся в агрегат частиц.

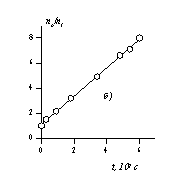
Расчет кинетических кривых по уравнениям (2.3.162) и (2.3.164) приводит к зависимостям, показанным на рис.2.25, а. На рис. 2.25, б приведена кинетическая кривая коагуляции в линейных координатах уравнения Смолуховского (2.3.163), используемая для определения постоянной скорости коагуляции.

Иногда расчеты постоянной скорости проводят теоретически, для чего используют уравнение Эйнштейна, связывающее коэффициент диффузии и размер частиц

, (2.3.165)

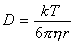
При выводе выражения для постоянной скорости коагуляции принимаем, что столкновение и слипание частиц происходит при их сближении на расстояние R = 2r, поэтому

D = kT /(3phR) . (2.3.166)

Подставляя уравнение (2.3.166) в выражение для постоянной скорости (2.3.161), получаем

к = 8kT/3h . (2.3.167)

Из этого выражения видим, что постоянная скорости коагуляции не зависит от размеров частиц, а определяется лишь вязким сопротивлением среды и температурой системы.

Для времени половинной коагуляции из уравнений (2.3.161) и (2.3.167) получаем уравнение

Следовательно, время половинной коагуляции также не зависит от свойств частиц, а является функцией начальной частичной концентрации, вязкости среды и температуры.

Рис. 2.25. Кинетические кривые коагуляции: а- порядок частиц (1 — суммарное число частиц, 2 – первый, 3 – второй, 4 – третий); б- кинетическая кривая, линейная форма уравнения Смолуховского

Видео:Вывод основного уравнения МКТ (самая убойная тема школы)Скачать

Кинетика коагуляции коллоидов

Видео:Вывод уравнения СлуцкогоСкачать

Теория быстрой перекинетической коагуляции по Смолуховскому

Часто под коагуляцией понимают как коалесценцию, так и коагуляцию.

Введем 4 приближения (условия анализа):

1. Допустим, что вначале система была монодисперсной, то есть состояла из частиц одинакового размера.
2. Пусть все частицы имеют сферическую форму.
3. Допустим, что вероятность встречи частиц во всех направлениях одинакова (поведение частиц определяется только броуновским движением). Коагуляция, при которой вероятность встреч частиц во всех направлениях одинакова, называется перекинетической. В этом случае скорость соединения частиц можно анализировать как кинетику обычных бимолекулярных реакций.
4. Допустим, что каждая встреча частиц приводит к их соединению. Кинетика, удовлетворяющая этому условию, называется быстрой коагуляцией.

Скорость бимолекулярной реакции рассчитывается по уравнению

где к — константа скорости реакции; «„ «, — концентрации /-х иj-x частиц.

Константу скорости коагуляции к можно представить из геометрических соображений.

где Д-и Dj — константы скорости диффузии частиц / и у; Л,- и /?, — радиусы частиц.

Допустим, что в начальном состоянии (время t = 0) система содержала п₀ исходных частиц радиусом R_<] в единице объема.

Тогда в некоторый момент времени / в системе будет

п_] — количество первичных частиц, полученных соединением двух исходных частиц;

п₂ — количество вторичных частиц, полученных соединением исходных и первичных частиц;

п_к — количество к-х частиц, полученных соединением /-й иу-й частиц, где к = i + у.

Скорость изменения числа к-х частиц (dnjdt) можно представить в виде разности скорости рождения частиц и скорости их исчезновения за счет встреч с любой другой. Найдем скорость зарождения новых частиц:

Суммируем по / произвольно до к- — все номера / — 0, 1,2, 3, 4. а у — принимает значения, дополняющие до к: у — . 4, 3, 2, 1, 0.

При таком способе счета каждая частица считается дважды, поэтому вводим коэффициент 1/2.

Найдем скорость изменения числа к-х частиц как разность между скоростью их зарождения и скоростью их исчезновения: dn_k

-г- = (скорость возникновения к-х частиц) — (скорость расходо- dt

вания к-х частиц.

Преобразуем эту разность, используя выражения для коэффициентов диффузии частиц:

Пока размеры частиц различаются не слишком сильно, выражением в скобках можно пренебречь, тогда

4-ДД, — такое приближение оправдано лишь в начале коагуляции или на последующих стадиях, когда частота встреч мала. Когда круглой скобкой пренебречь нельзя, тогда коагуляция не перекинетическая:

Изменение общего числа частиц в системе найдем, суммируя все п_к

Каждую двойную сумму можно представить в виде квадрата одной из сумм, так как значения число пробегает одни и те же, хотя индексы разные.

(удобнее оставить индекс к, так как слева у нас тоже к).

Так как суммируем от 0 до то пределы больше ставить не будем:

Разделим переменные:

Строго говоря, здесь вариация, а не дифференциал. После интегрирования получаем

t = 0; 2-, п к =п о — начальные условия. Отсюда с =—;

«о

Общее число частиц в системе в момент времени 1 рассчитывается по уравнению:

1. Общее число частиц зависит от исходного числа частиц. Эта зависимость четко сказывается лишь в первый момент времени t. Когда n₀t»1, то п₀ сокращается и общее число частиц не будет зависеть от их начального числа п₀.
2. При данной концентрации исходных частиц п₀ сумма зависит от комплекса D₀r₀, а этот комплекс:

Следовательно, Iп_к не зависит от исходных размеров частиц:

С увеличением вязкости среды сумма Zn_k возрастает, то есть уменьшение числа частиц с ростом вязкости замедляется.

Обычно скорость коагуляции характеризуют временем, в течение которого исходное число частиц уменьшается вдвое. Это время называют временем коагуляции т_|/2.

Время коагуляции растет пропорционально вязкости и обратно пропорционально температуре и исходной концентрации частиц.

Быстрая перекинетическая коагуляция может иметь место при укрупнении мелких пузырьков в оксидном расплаве, когда отсутствуют сильные конвективные токи. Принимая для силикатного расплава вязкость г| = 5 пуаз при температуре Т= 1873 К, получим

Анализ этого уравнения показывает, что при исходной концентрации газовых включений в силикатном расплаве п

10 s шт./см 3 время коагуляции т,_/2 = 1,45 • 10 3 сек

За 40 часов число газовых включений в силикатном расплаве уменьшится вдвое. Следовательно, из оценочных расчетов вытекает, что даже быстрая коагуляция не может обеспечить достаточной скорости укрупнения пузырьков.

Видео:Законы Кирхгофа. Метод контурных уравненийСкачать

Лако-красочные материалы — производство

Видео:Решение задач на вывод формул органических соединений | Химия 10 класс #8 | ИнфоурокСкачать

Технологии и оборудование для изготовления красок, ЛКМ

Видео:Секретный вывод основного уравнения МКТСкачать

КИНЕТИКА КОАГУЛЯЦИИ

Прежде чем перейти к обсуждению причин устойчивости и коагуляции лиозолей, рассмотрим теорию кинетики коагуляции, которая, кстати говоря, была разработана гораздо раньше теории устойчивости коллоидных систем.

Различают быструю и медленную коагуляцию. Под быстрой коагуляцией подразумевают такую коагуляцию, при которой все сближения частиц, находящихся в броуновском движении, кончаются их слипанием. При медленной коагуляции вследствие того, что на поверхности коллоидных частиц частично сохранился двойной электрический слой^сольвауная оболочка и т. д., слипание ча — стйцПп^»йсхбдатг»лишь» в результате особо удачных сближений. Таким образом, оба термина являются вполне условными.

Теория кинетики быстрой коагуляции создана польским ученым Смолуховским. Основные положения, из которых исходил Смолуховский, сводятся к тому, что между частицами золя действуют силы притяжения и отталкивания; последние ослабевают при введении электролита и при концентрации электролита, вызывающей быструю коагуляцию, исчезают вовсе. Дальнейшее прибавление электролита не может ускорить коагуляцию. Частицы такого астабилизованного золя при сближении в процессе броуновского движения на достаточно близкое расстояние слипаются под давлением сил молекулярного притяжения, образуя агрегат, который совершает в дальнейшем броуновское движение как одно целое. Природу сил, действующих между частицами, Смолуховский не рассматривал.

Для экспериментального изучения кинетики коагуляции необходимо было определить изменение концентрации частиц в золе по мере коагуляции. Это можно было бы осуществить путем счета частиц с помощью ультрамикроскопа. Однако определение численной концентрации таким методом весьма длительно, а коагуляция протекает обычно очень быстро, так что к концу счета концентрация частиц в золе оказалась бы совсем иной, чем в его начале. Выход был найден в том, что в золь, в который был уже введен электролит и который таким образом находился в состоянии коагуляции, в определенный момент вводился стабилизатор, «обрывающий» коагуляцию. В таком стабилизованном золе численная
концентрация частиц уже не меняется и его можно исследовать с помощью ультрамикроскопа. В качестве стабилизатора для «обрыва» коагуляции обычно применялся желатин. В настоящее время метод, основанный на счете частиц в неподвижном объеме, не — применяется.

Кювременный метод изучения процесса коагуляции основан на счете частиц в потоке. Поточный ультрамикроскоп, разработанный впервые Б. В. Дерягиным и Г. Я. Власенко, описан в гл. II. Этим прибором можно определять численную концентрацию, не прерывая процесса коагуляции, во много раз быстрее, чем по старому способу. Одновременно новый способ устраняет многие источник»

Ошибок, присущие старому методу измерения численной концентрации золя. Недавно этот метод был усовершенствовав Мак Файденом и А. Смитом.

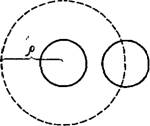
Смолуховский при создании своей теории принимал, что скорость быстро» коагуляции, т. е. изменение численной концентрации частиц в единицу времени, зависит от численной концентрации золя v, от интенсивности броуновского движения, характеризующейся коэффициентом броуновской диффузии частиц D, и от критического расстояния р, на которое должны приблизиться друг к другу центры двух частиц, чтобы произошло слипание частиц. Расстояние р может превышать диаметр коллоидных частиц, (рис. IX, 1). Таким образом, если представить се, бе сферу радиуса р, центр которой совпадает с центром одной из частиц, друга» частица прилипнет к ней только тогда, когда центр второй частицы коснется поверхности этой сферы, называемой сферой поглощения. При расстояниях, больших р, действием молекулярных сил притяжения на броуновское движение частиц и на процесс их. сближения Смолуховский полностью пренебрегал.

Рис. IX, 1. Схема, поясняющая сферу действия частиц при быстрой коагуляции.

При быстрой коагуляции агрегация, согласно Смолуховскому, идет таким образом, что первоначальные одинарные частицы, сталкиваясь друг с другом, образуют двойные частицы, затем двойные частицы, сталкиваясь с одинарными, образуют тройные и т. Д — Возможны столкновения между собой и сложных частиц. Одновременное столкновение трех н более простых или сложных частиц возможно, но вследствие малой вероятности такого события Смолуховский для упрощения теории не принимал в расчет подобные столкновения.

Обозначая через vi, V2r V3 … численные концентрации частиц, состоящих из одной, двух, трех и т. д. первоначальных частиц, можно написать, что в начале, когда время т = О

V, = v0 и va = v3 = … v„ = О

По истечении времени т

V = vt = Vj + v2 + v3 + … где v — конечная численная концентрация.

При этом, очевидно, будет соблюдаться неравенство:

Но Д, = 0 и Ді = 0, так как все направления смещений равновероятны. Поэтому Д, Ді = 0 и, следовательно

Таким образом, средние квадраты смещений всех частиц относительно первой удваиваются. Благодаря связи Д2 с коэффициентом диффузии можно сказать, что броуновское движение остальных частиц относительно первой характеризуется вдвое большим коэффициентом диффузии D‘. В результате этого время от времени частицы будут сближаться с первой до критического расстояния их Центров р. Подсчитаем число таких сближений, не учитывая тех осложнений, которые возникают при изменении броуновского движения вследствие слипания частиц. Для этого примем, что после сближения частиц до расстояния центров р соответствующая частица как бы поглощается центральной. Пусть частицы заключены в очень большой объем. Допустим также, что в рассматриваемый момент коагуляции численная концентрация v равна vT. Однако в непосредственной близости от поверхности поглощающей сферы концентрация частиц близка к нулю, так как ввиду беспорядочного характера броуновского блуждания вероятность попадания частицы, находившейся вблизи поглощающей сферы, в эту сферу очень велика, а вероятность избежать этого мала. При удалении от сферы р быстро достигаются значения vT. Совокупное перемещение частиц, совершающих независимо друг от друга беспорядочные блуждания, описывается уравнением диффузии. Допустим, что концентрация частиц v(R) зависит только От расстояния R от начала координат, к которому направлен поток диффузии, вызванный поглощением частиц сферой радиуса р. В этом случае из законо» диффузии следует:

Где Q — число частиц, проходящих за единицу времени через поверхность сферы s радиуса R по направлению к центральной частице.

Число Q, очевидно, равно числу частиц, поглощенных за единицу времена центральной частицей при сближении с ней, т. е. Q равно искомой частоте актов агрегации с участием центральной частицы.

Учитывая граничное условие

Которое следует из того, что частицы, достигнув сферы р, поглощаются центральной частицей, и интегрируя уравнение (IX, 5), получим:

Учитывая другое граничное условие

Общее число сближений всевозможных частиц в единице объема можно определить, умножая Q на численную концентрацию v и деля полученное произведение на 2, так как иначе каждая пара частиц будет подсчитана дважды. Заменяя D‘ на 2D, получим:

Сравнивая это уравнение с уравнением (IX, 1), мы найдем значение константы к в уравнении Смолуховского (IX, 2):

Следует заметить, что формула Смолуховского предполагает существование начального момента коагуляции, до которого слипания частиц не происходило. Поэтому в начальный момент центральная частица окружена частицами, концентрация которых всюду равняется Vo. Вследствие этого в начале процесса Коагуляции частота сближения и слипаний несравненно больше, чем величина Q В уравнении (IX, 9). Однако очень скоро именно благодаря высокой начальной частоте сближений концентрация частиц вблизи центральной уменьшается до нуля, и за доли секунды установится распределение частиц, подчиняющееся уравнению (IX, 6). После этого скорость коагуляции будет подчиняться уравнению Смолуховского.

Однако через некоторое время начнутся отклонения от закона Смолуховского, Основная причина заключается в том, что коэффициент к в формуле (IX, 2), выведенный при рассмотрении процесса сближения двух одинарных частиц, принимает иное значение при сближении с агрегатом слипшихся частиц другого агрегата или даже одиночной частицы.

Придав уравнению (IX, 1) вид:

И проинтегрировав его в пределах от vo до v и от 0 до т, получим:

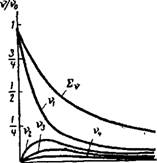
Рнс. IX, 2. Зависимость относительного числа частиц различного порядка от т/0 при быстрой коагуляции.

Откуда численная концентрация золя в момент т будет равна:

Вводя время половинной коагуляции 9, можем написать

Тогда основное уравнение (IX, 12) можно представить так:

По уравнению IX, 14, зная vo и v для различных значений т, можно вычислить 0 и к.

Графически зависимость относительных изменений общего числа частиц £ v и числа частиц vi, V2, V3 … в единице объема золя от т/0 показана на рис. IX, 2. Из уравнения (IX, 14) следует, что 1/v есть линейная функция времени т. Это следствие теории неоднократно было подтверждено на опыте.

Теория Смолуховского позволяет также вычислить расстояния р, на которые должны приблизиться центры двух частиц для того, чтобы произошло их слипание.

Kv0 4itЈ>pv0 И, согласно Эйнштейну,

Где K — константа Больцмаиа; т) — динамическая вязкость дисперсионной среды; Г — радиус частиц,

То, комбинируя два последних уравнения, получим:

Согласно эксперименту, р/г = 2,3, следовательно, расстояние р довольно близко к 2г, т. е. силы аттракции начинают действовать

Лишь тогда, когда частицы приблизятся на весьма малые расстояния, на которых энергия ‘молекулярного притяжения становится намного больше энергии теплового, а следовательно, и броуновского движения 3likT.

Представления Смолуховского объясняют коагуляцию монодисперсных золей. Мюллер разработал подобную же теорию для объяснения коагуляции полидисперсных систем. Он показал, что частицы различных размеров агрегируются всегда скорее, чем одинаковые частицы. При этом большие частицы играют роль как бы «зародышей» коагуляции; такую же роль могут играть и агрегаты, образующиеся в начальной стадии коагуляций приблизительно монодисперсного золя золота, как об этом свидетельствуют наблюдения Б. В. Дерягина и Н. М. Кудрявцевой. Впрочем, положения Мюллера полностью верны лишь тогда, когда в золе имеются частицы, существенно превосходящие по размеру малые частицы. Теория Мюллера объясняет автокаталитический характер коагуляции, скорость которой может постепенно возрастать со временем. Мюллер также показал, что коагуляция ускоряется, если частицы имеют удлиненную форму, так как на поступательное броуновское движение налагается еще вращательное движение, увеличивающее вероятность столкновения таких частиц.

Теория СМолуХовского, как мы неоднократно подчеркивали,, пригодна «Для быстрой коагуляции. Им было сделано предположение, что разработанная «теория может быть приложима и к медленной коагуляции, когда частицы не полностью астабилизованьи В этом случае в уравнение IX, 12, описывающее процесс коагуляции, следует ввести эффективность сближения є:

Однако, как следует из теории коагуляции Н. А. Фукса, приложи — мой к частицам, силы взаимодействия между которыми изменяются с расстоянием по любому закону, параметру є надо придать другой смысл, так как понятие эффективности сближения по Смо — луховскому неприменимо к процессу сближения частиц, совершающих броуновское движение.

Теория Смолуховского предполагает, что до сближения частиц на определенное расстояние р никаких сил взаимодействия между ними нет. Для учета сил дальнодействия частиц, как функции от расстояния их центров R, Н. А. Фукс дополнил формулу (IX, 5) членом, выражающим дрейф частиц по направлению к центральной частице под влиянием сил притяжения F:

Где Р — подвижность частицы в вязкой среде, равная отношению ее скорости к действующей силе; цифра 2 перед р введена потому, что в действительности обе частицы движутся навстречу друг другу.

Согласно Эйнштейну р = D/kT, следовательно, 2|3 = D‘/kT. Далее, заменяя силу F на dU/dR (где U — потенциальная энергия молекулярного взаимодействия двух частиц) и интегрируя уравнение (IX, 18), вместо (IX,9) получим:

При £/(/?)= О снова получается формула (IX, 9). Уравнение (IX, 19) было выведено Н. А. Фуксом первоначально для аэрозолей с целью учета ускорения коагуляции под влиянием притяжения разноименно заряженных частиц. В этом случае потенциальная энергия взаимодействия отрицательна и скорость коагуляции возрастает.

В общем случае из (IX, 19) вместо (IX, 10) можно получить уравнение

И вместо константы Смолуховского к величину, меньшую в W раз, где

Величину W называют коэффициентом замедления. Легко видеть, что уравнение медленной коагуляции получится путем замены е на 1 /W. Таким образом, теория Фукса дает теоретическое истолкование коэффициента Смолуховского е.

Для коллоидной химии особый интерес представляет случай, когда между частицами преобладают силы отталкивания. При этом U(R)> 0, и если для каких-то значений R величина U<R) Много больше, kT, то значение Q становится крайне малым. Это Значит, Что скорость коагуляции настолько снизится, что можно говорить о практической агрегативной устойчивости системы.

Для исследования кинетики коагуляции Б. В. Дерягиным и Н. М. Кудрявцевой был применен поточный ультрамикроскоп (по схеме, близкой к поточному ультрамикроскопу для аэрозолей Б. В. Дерягина и Г. Я. Власенко). С помощью поточного ультрамикроскопа можно определять за 2—3 мин численную концентрацию гидрозолей вплоть до 1010—10″ частиц в 1 см3; другие способы счета частиц не позволяют измерять концентрацию больше 10*— 105 частиц в 1 см3. При применении достаточно концентрированных золей с помощью поточного микроскопа можно наблюдать не только быструю, но и медленную коагуляцию, отвечающую малым значениям коэффициента е, не затрачивая для этого чрезмерно много времени.

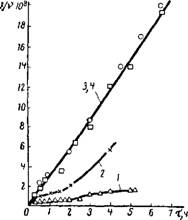
На рис. IX, 3 приведены графики зависимости І/v от времени т, прошедшего от начала коагуляционного процесса для сравнительно низкодисперсного голубого гидрозоля золота; отдельные кривые отвечают различным концентрациям коагулирующего электролита. Можно видеть, что при высокой концентрации электролита (кривые 3 и 4), при которой потенциальный барьер * исчезает, кинетика коагуляции характеризуется линейной зависимостью, вытекающей из теории

Смолуховского. Несколько меньший наклон прямой к оси абсцисс объясняется согласно В. М. Муллеру тем, что на близких расстояниях вязкое сопротивление жидкой прослойки сближению сферических частиц возрастает по сравневию с сопротивлением, рассчитанным по формуле Стокса При малых концентрациях электролита линейная зависимость ^кривые 1, 2) нарушается. Типичной является кривая 2. После начального подъема кривой следует участок, почти параллельный оси абсцисс, и в некоторый момент происходит новый подъем кривой, в дальнейшем не прекращающийся. Согласно Б. В. Дерягину и Н. М. Кудрявцевой первоначальный подъем кривой и, следовательно, уменьшение численной концентрации золя означает образование агрегатов из двойных частиц. При малых концентрациях электролита ближняя потенциальная яма сравнительно не глубока, энергетические взаимодействия не велики и потому распады образовавшихся двойных частиц происходят с достаточной частотой.

Прн достижении определенной концентрации двойных частиц их распады уравновешивает процесс слипания одиночных частиц, вследствие чего численная концентрация золя становится постоянной. В некоторый момент к одной из двойных частиц прилипает третья частица, образуя тройную частицу. Энергия связи каждой из трех частиц образовавшегося агрегата в два раза больше, чем у частицы, входящей в двойную частицу. Поэтому такая тройная частица имеет мало шансов распасться. Одновременно происходит дальнейший рост агрегатов за счет присоединения новых частиц. И действительно, визуальные наблюдения под микроскопом показали, что в некоторый момент среди сравнительно слабо видимых частиц (по «вспышкам» в поле зрения поточного ультрамикроскопа) появляются все более яркие и коагуляция все более ускоряется. Этнм объясняется форма кривых с перегибом. При более высоких концентрациях электролита вследствие снижения энергетического барьера и углубления потенциальной ямы горизонтальные участки графика укорачиваются и, наконец, исчезают, ио S-образная форма кривых сохраняетсяГТаким образов, при изучении коагуляции необходимо учитывать не только процессы агрегации, но и распада агрегатов.

Дальнейшее развитие этих положений принадлежит Г. А. Мартынову и В. М. Муллеру. В определенных условиях может устанавливаться агрегативное равновесие между одинарными и агрегированными частицами. Хотя вероятность распада крупных агрегатов меньше, чем парных, все же уменьшение числа одинарных частиц в конечной стадии коагуляции может настолько понизить скорость образования новых агрегатов, что коагуляция будет уравновешена скоростью распада агрегатов. Следовательно, возможно равновесие между коагулятом и оставшимся разбавленным золем. Это явление, однако, не носит общего характера, так как существуют золи, коагулирующие необратимо, и обнаруженное поведение золей золота в работе Н. М Кудрявцевой, по-видимому, связано с частичной гидрофилизацией поверхности его частиц за счет адсорбции органических компонентов, остающихся в золе после его приготовления.

Рис. IX, 3. Кинетика коагуляции голубого гидрозоля золота в присутствии хлорида кални. Концентрация коагулирующего электролита (в моль/л): 1—5-Ю-3; 2—1 • Ю-2; 3 —5 • Ю-2; 4 — 1 • Ю-1.

Следует отметить, что учет образования и распада агрегатов и его ускорения в градиентном потоке, как было показано уже давно Гудивом, Жнллепси и др., позволяет объяснить реологическое поведение тиксотропных суспензий, о чем будет сказано в гл. X.

От распада агрегатов в процессе коагуляции следует отличать явление пептизации — распада агрегатов в результате изменения ионного состава дисперсионной среды, о чем уже говорилось в гл. VIII. В этом случае пептизация происходит благодаря усилению электрической слагающей расклинивающего давления и уменьшению глубины потенциальной ямы.