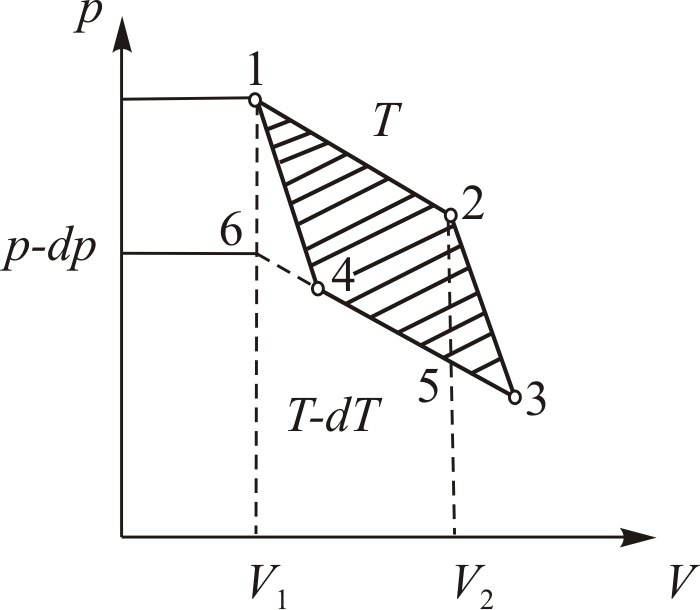
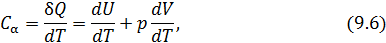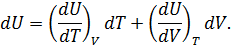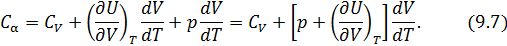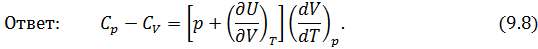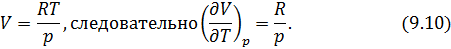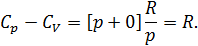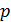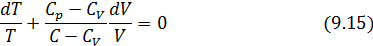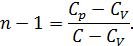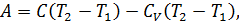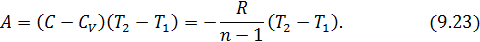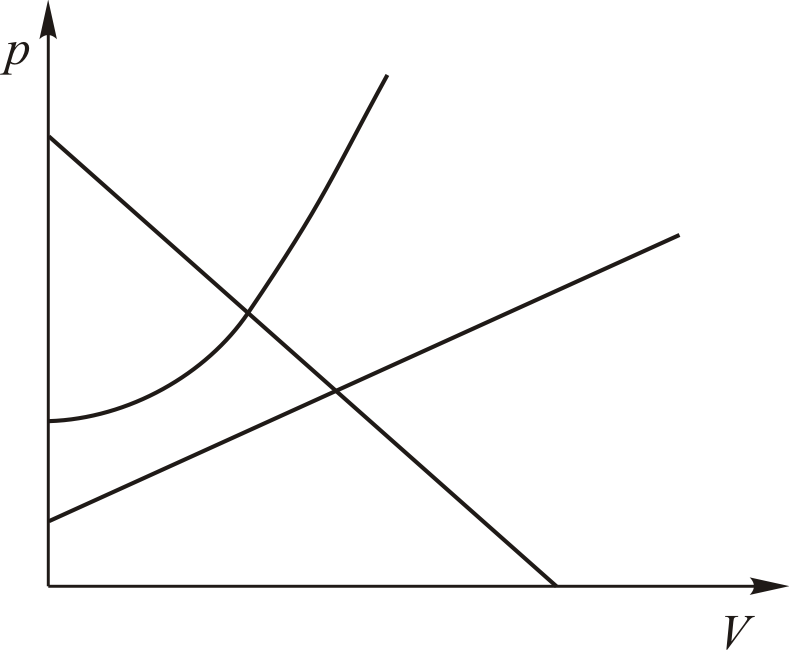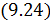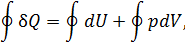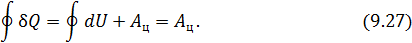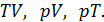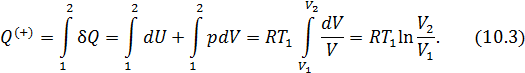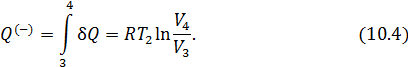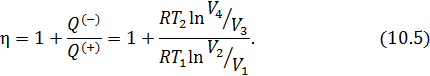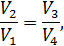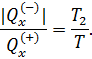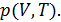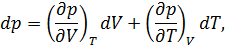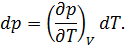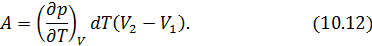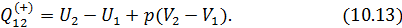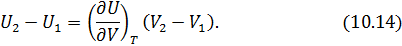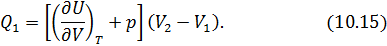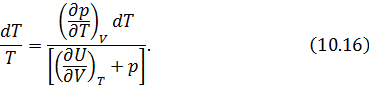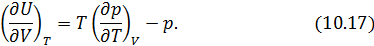• Воспользовавшись записью первого начала термодинамики в дифференциальной форме (9.2), получим выражение для теплоёмкости произвольного процесса:
• Представим полный дифференциал внутренней энергии через частные производные по параметрам 
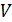
После чего формулу (9.6) перепишем в виде
Соотношение (9.7) имеет самостоятельное значение, поскольку определяет теплоёмкость 
• Рассмотрим процесс при постоянном давлении 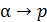
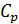
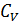
Исходя из полученной формулы, можно легко найти связь между теплоемкостями 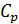
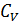
Уравнение Роберта Майера
Выразим частные производные в правой части уравнения (9.8), с помощью термического и калорического уравнений, записанных для одного моля идеального газа. Внутренняя энергия идеального газа зависит только от температуры и не зависит от объёма газа, следовательно
Из термического уравнения легко получить
Подставим (9.9) и (9.10) в (9.8), тогда
Вы, надеюсь, узнали (9.11). Да, конечно, это уравнение Майера. Еще раз напомним, что уравнение Майера справедливо только для идеального газа.
9.3. Политропические процессы в идеальном газе
Как отмечалось выше первое начало термодинамики можно использовать для вывода уравнений процессов, происходящих в газе. Большое практическое применение находит класс процессов, называемых политропическими. Политропическим называется процесс, проходящий при постоянной теплоемкости 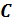
Уравнение процесса задается функциональной связью двух макроскопических параметров, описывающих систему. На соответствующей координатной плоскости 
Вывод уравнения политропического процесса в идеальном газе
• Требование постоянства теплоёмкости 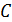
• Используя уравнение Майера (9.11) и уравнение состояния идеального газа, получаем следующее выражение для
• Разделив уравнение (9.12) на T и подставив в него (9.13) придем к выражению
• Разделив ( 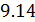
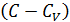
• Интегрированием (9.15), получаем
Это уравнение политропы в переменных
Исключая из уравнения ( 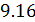

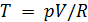
Параметр 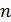
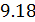
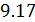
К этому классу процессов относится также адиабатный или адиабатический процесс. Адиабатным называется процесс, проходящий без теплообмена ( 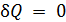
Из определения теплоемкости следует, что в адиабатическом процессе 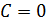
где 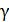
В этом случае уравнение политропы принимает вид
Уравнение адиабатного процесса (9.20) называют также уравнением Пуассона, поэтому параметр 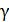
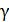
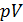
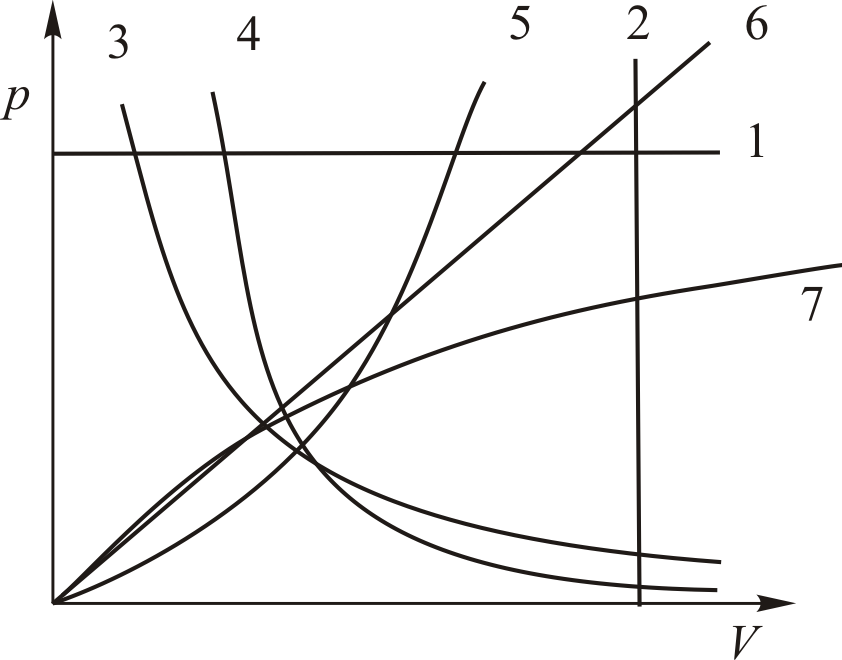
Графики политропических процессов для различных значений 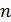
На рис. 9.1 графики процессов пронумерованы в соответствии с табл. 9.1.
| Номер политропы на рис. 9.1 | Значение показателя политропы | Уравнение политропы ( 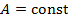 ) ) | Название процесса |
 | 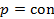 st st | изобарический | |
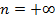 | 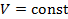 | изохорический | |
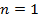 | 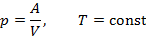 | изотермический | |
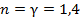 | 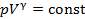 | адиабатический | |
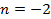 | 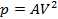 | — | |
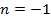 | 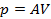 | — | |
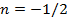 | 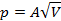 | — |
Знание показателя политропы 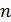
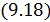
Тогда, бесконечно малое количество теплоты, сообщённое макросистеме в политропическом процессе равно
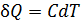
Соответственно полное количество теплоты, полученное системой при изменении её температуры от 

Зная 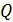
Таким образом, мы можем получить исчерпывающую информацию об энергообмене системы с окружающей средой.
Теперь уместно поставить следующие вопросы. Что делать, если процесс не политропический? Можно ли глядя на график процесса, догадаться, что это не политропа?
Иногда можно. Взгляните на рис. 9.2. Это уж точно не политропы.
Для подобных процессов количество теплоты рассчитать не так просто как в случае политропных процессов 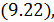
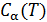
Полное количество теплоты, полученное системой в произвольном процессе, можно рассчитать только интегрированием
Вычисление теплоемкости и количества теплоты в различных процессах является внутренней подзадачей многих учебных задач, с которыми вы встретитесь при изучении термодинамики.
9.4. Тепловые машины и их эффективность.
Циклические процессы являются основой действия тепловых машин. В используемых на практике разнообразных тепловых машинах реализованы различные виды термодинамических циклов. Тепловыми машинами являются двигатели внутреннего сгорания, реактивные двигатели, холодильники, кондиционеры, тепловые насосы, паровые турбины и т. д.
| Рис. 9.3. |
Работа расширения 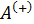
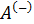
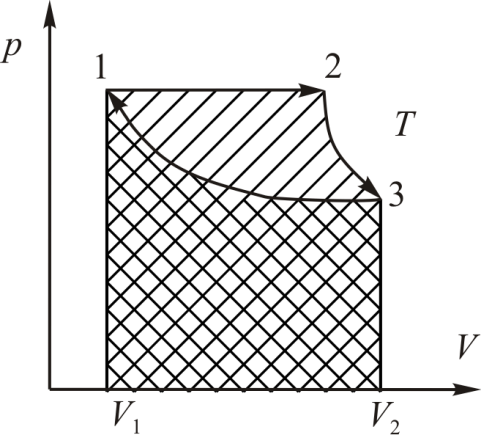
Действительно, проинтегрировав по циклу равенство, выражающее первое начало термодинамики, получим важный результат:
из которого следует, что работа равна количеству теплоты, полученной системой за цикл
Теплота в каких-то частях цикла поступает в систему ( 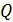
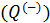
Определить поступает в систему количество теплоты или оно теряется иногда можно только расчётом, но зачастую это видно на графике процесса:
• Если температура 
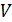
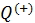
• Если температура 
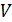
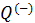
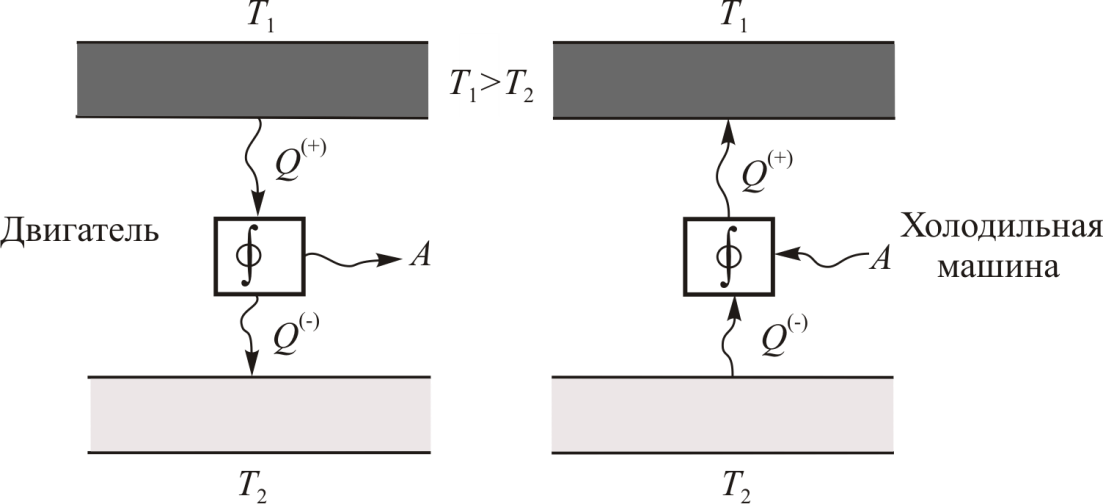
Принципиальная схема работы тепловой машины
Схематически работа машин по прямому и обращенному циклу представлена на рис. 9.4 и 9.5. Любая машина должна включать в себя нагреватель с температурой 

Принцип работы двигателя: в процессе работы машина получает количество теплоты от нагревателя, часть которого идёт на совершение полезной работы (приводится в действие какой-либо силовой агрегат), а часть отдаётся холодному резервуару.
Принцип работы холодильной машины: для того, чтобы отобрать количество теплоты от холодильника и передать его нагревателю, необходимо затратить некоторое количество энергии на совершение механической работы над рабочим веществом машины.
Показатели эффективности тепловых машин
Эффективность двигателя характеризуется коэффициентом полезного действия η (КПД). Эффективность холодильной машины – коэффициентом использования энергии ξ(КИЭ). На схеме 9.4.1 приведены формулы для вычисления КПД и КИЭ.
| Коэффициент полезного действия тепловой машины |
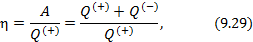  |
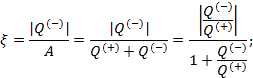 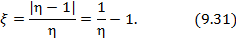 |
| Коэффициент использования энергии холодильной машины |
Чтобы воспользоваться формулами 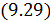
1. Сформулируйте первое начало термодинамики. Запишите его уравнение в дифференциальной форме, поясните обозначения бесконечно малых величин. К каким процессам применим этот постулат?
2. Что называется вечным двигателем первого рода?
3. Как определяются теплоемкости при постоянном объеме и при постоянном давлении? Почему их называют функциями состояния?
4. Получите уравнение, связывающее теплоемкости 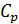
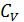
5. Сделайте вывод уравнения Майера. Для каких систем это уравнение применимо?
6. Что называется политропическим процессом? Запишите уравнение политропы для параметров
7. Как связан показатель политропы с теплоемкостью процесса?
8. Является ли адиабатный процесс политропическим процессом? Обоснуйте ответ.
9. Как выглядят графики политропических процессов? Приведите примеры.
10. Как можно определить работу, совершенную системой, через количество теплоты, полученное ею извне в политропическом процессе?
11. Нарисуйте принципиальные схемы тепловых машин, работающих как двигатель и как холодильная машина.
12. Дайте определения КПД и КИЭ. По каким формулам они вычисляются и как связаны между собой?
ТЕОРЕМЫ КАРНО И ИХ ПРИЛОЖЕНИЯ
В 1824 году французский физик и военный инженер Никола Леонар Сади Карно опубликовал свою работу «Размышления о движущей силе огня и о машинах, способных развивать эту силу», в которой им были сформулированы основные положения теории тепловых машин, содержащие по своей сути идею второго начала термодинамики.
В этом сочинении Карно ввёл в научный обиход множество понятий, использующихся в термодинамике и сейчас. Однако главной заслугой учёного стало выдвижение идей о необходимости перепада температур для создания циклически действующей тепловой машины и о том, что величина работы определяется только разностью температур нагревателя и холодильника и не зависит от природы рабочего вещества.
| Рис. 10.1. |
В идеальной машине Карно рабочее вещество (идеальный газ) совершает цикл, представленный на рис. 10.1, состоящий из двух изотерм и двух адиабат. Адиабата и изотерма слабо отличаются друг от друга, поэтому площадь внутри замкнутой кривой на диаграмме 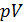
Расчёт КПД машины Карно
Идеальный газ совершает цикл, состоящий из двух изотерм и двух адиабат – цикл Карно, представленный на рис. 10.2.
Актуальная информация о системе и процессах
• Так как газ идеальный, то справедливо уравнение Клапейрона-Менделеева
• Изменение внутренней энергии идеального газа на изотерме равно нулю
• Уравнение адиабаты для идеального газа в параметрах 
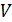
Рассчитать КПД тепловой машины Карно.
• По определению КПД двигателя равен
• Количество теплоты, поступающее к рабочему телу от нагревателя на
участке 1-2 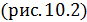
При записи (10.3) учтено, что изменение внутренней энергии идеального газа на изотерме не происходит.
• На участке 3-4 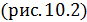

• На участках 2-3 и 4-1 рабочее тело изолируется от нагревателя и холодильника. Соответствующие квазистатические процессы идут без теплообмена
• Подставим в формулу (10.2) полученные значения 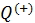
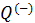
• Уравнение адиабатического процесса (10.1) позволяет существенно упростить это выражение. Действительно, для адиабаты 2 — 3 (рис. 10.2)
а для адиабаты 4 — 1 запишем
Если разделить уравнение (10.6) на уравнение (10.7), то получим
• Воспользовавшись этим результатом, из формулы (10.5) получим окончательный ответ
Из (10.9) видно, что чем ниже температура холодильника 

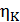



10.2. Теоремы Карно
Основные положения теории тепловых машин Сади Карно сформулировал в виде двух теорем, которые доказываются от противного [12]. Мы приведём лишь формулировки этих теорем и сфокусируем внимание на их приложениях (схема 10.2.1).
| Формулировки |
| Первая теорема Карно |
| Вторая теорема Карно |
| КПД тепловой машины, работающей по произвольному циклу с фиксированной максимальной и минимальной температурой, не превосходит КПД машины, работающей по циклу Карно с соответствующими температурами нагревателя и холодильника. |
| КПД машин, работающих по циклу Карно, не зависит от рабочего вещества и конструктивных особенностей машины, а определяется только температурами нагревателя и холодильника. |
| Приложения |
| • Построение абсолютной термодинамической шкалы температур. • Разработка метода теоретической термодинамики – метода циклов. |
| • Вывод неравенства Клаузиуса. • Определение энтропии в термодинамике. • Оценка эффективности тепловых машин сверху. |
Далее мы подробно рассмотрим каждое из приложений этих двух теорем. Начнем с построения абсолютной термодинамической шкалы температур.
Термодинамическая шкала температур
Поскольку КПД не зависит от рабочего тела, то можно представить следующую процедуру построения шкалы температур.
• В качестве нагревателя машины Карно берется некоторое стандартное тело, например, вода, кипящая при атмосферном давлении.
• В качестве холодильника выбирается другое стандартное тело, например лед, тающий при атмосферном давлении.
• Разность температур 

• Осуществляется обратимый цикл Карно с каким-либо телом.
• Измеряются 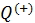
Кроме того 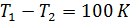




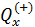
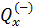
Отсюда находится искомая температура 
Построенная таким образом шкала температур Кельвина, как мы уже знаем, совпадает со шкалой газового термометра. Из уравнения (10.10) следует, что нулем температуры является температура, при которой 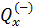
10.3. Метод циклов
С помощью первой теоремы Карно можно получить много важных соотношений между физическими величинами в дифференциальной форме, характеризующими систему в состоянии термодинамического равновесия. Для этого надо заставить систему надлежащим образом осуществить цикл Карно и применить к нему теорему Карно. Этот метод называется методом циклов. Проясним его сущность на примере решения следующей задачи.
Задача о нахождении зависимости внутренней энергии
макроскопического тела от его объема
Рассмотрим произвольное физически однородное тело, состояние которого характеризуется двумя параметрами 
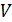
известно его термическое уравнение состояния
Для того, чтобы в соответствии с методом циклов получить зависимость энергии от объема в дифференциальной форме, необходимо осуществить бесконечно малый цикл Карно над рассматриваемым телом таким образом, чтобы температуры изотерм отличались на 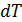

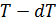
Запишем КПД цикла Карно с одной стороны через температуры, а с другой – через полученное телом количество теплоты и совершенную им работу
Работа 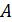
Высота этого параллелограмма численно равна приращению
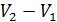
Основание же 6-1дает приращение давления при повышении температуры на 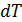
Для работы цикла, которая численно равна его площади, получаем
Вычислим теперь количество теплоты 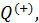
Так как на изотерме 1-2температура постоянна, то
Подставив (10.14) в (10.13), получим
Теперь вернемся к (10.11). Выразим числитель и знаменатель правой части этого уравнения согласно (10.12) и (10.15). Тогда получим
Из (10.16) легко выразить частную производную. В итоге получаем искомое решение
Подобным образом можно найти зависимость давления насыщенного пара от температуры или закон изменения поверхностного натяжения с температурой и множество других закономерностей.
10.4. Неравенство Клаузиуса. Определение энтропии
На основе второй теоремы Карно можно получить неравенство, связывающее приведённую теплоту нагревателя 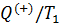
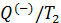
где 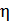


Запишем это неравенство более детально
или, что, то же самое
Знак минус в этом неравенстве показывает, что 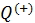
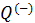
Отметим, что знак равенства относится к равновесному циклу Карно, а знак неравенства к неравновесному (необратимому).
Неравенство Клаузиуса можно обобщить для произвольного цикла [12]. Оно имеет следующий вид
здесь под 
Запишем (10.20) для произвольного обратимого цикла
Из этого следует (см. 8.1), что бесконечно малая величина под интегралом в (10.21) является полным дифференциалом некоторой функции состояния. Обозначим её буквой 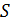
Равенство (10.22) определяет энтропию для обратимых процессов. Дальнейшему обсуждению этой важной термодинамической величины будет посвящена следующая лекция. Кроме того, свойства энтропии в окрестности абсолютного нуля температур мы рассмотрим при изучении третьего начала термодинамики.
10.5. Оценка эффективности тепловых машин сверху
В повседневной жизни мы постоянно используем различные виды тепловых машин. Наземные транспортные средства невозможно представить без бензинового двигателя внутреннего сгорания или дизельного мотора. На тепловых электростанциях работают паровые турбины. В небо нас уносят турбореактивные самолеты. В основе работы этих и многих других машин лежат различные циклические процессы и в них применяются разные рабочие вещества. У вас будет возможность научиться рассчитывать КПД и КИЭ на основе рассмотрения конкретных циклов Отто, Дизеля, Брайтона и других. Возникает вопрос, можно ли рассчитать показатели эффективности машины, не вдаваясь в детали ее работы. Оказывается можно, но, разумеется, приближенно. Вторая теорема Карно позволяет сделать оценки эффективности реальных машин сверху. Для этого нужно знать только максимальную температуру цикла машины 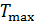
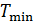
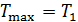
будем рассчитывать КПД и КИЭ реальных машин по формулам цикла Карно. Эти формулы приведены на схеме 10.5.1.
| Эффективность идеальной машины Карно |
| Коэффициент использования энергии |
| Коэффициент полезного действия |
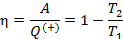 |
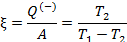 |
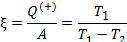 |
| Тепловой насос |
| Холодильник, кондиционер |
| Двигатель |
Примеры оценок эффективности тепловых машин сверху
КПД бензинового двигателя внутреннего сгорания




КПД реального теплового двигателя, работающего по циклу Отто, не превосходит 0,56.
- Политропный процесс | 20+ важных часто задаваемых вопросов и числовых значений
- Content
- Политропный процесс
- Определение политропный процесс
- Политропное уравнение | Политропное уравнение состояния
- Политропный индекс
- Политропные работы
- Политропная теплопередача
- Политропный против изэнтропического процесса
- Политропный процесс против адиабатического процесса
- Политропная эффективность
- Политропная голова
- Политропный процесс для воздуха | Политропный процесс для идеального газа
- Примеры политропных процессов
- 1. Рассмотрим политропный процесс с индексом политропы. п = (1.1). Начальные условия: P1 = 0, В1 = 0 и заканчивается на P2= 600 кПа, В2 = 0.01 м 3 . Оцените проделанную работу и теплоотдачу.
- 2. Поршневой цилиндр содержит кислород при 200 кПа объемом 0.1 м. 3 и при 200 ° С. Масса добавляется так, чтобы газ сжимался с PV. 1.2 = постоянная до конечной температуры 400 ° C. Подсчитайте проделанную работу.
- 3. Рассмотрим аргон при 600 кПа, 30 ° C, сжатый до 90 ° C в политропном процессе с n = 1.33. Найдите проделанную работу на Газе.
- 4. Предположим, что масса 10 кг ксенона хранится в баллоне при 500 К, 2 МПа, расширение представляет собой политропный процесс (n = 1.28) с конечным давлением 100 кПа. Посчитайте проделанную работу. Учтите, что система имеет постоянную удельную теплоемкость.
- 5. Рассмотрим цилиндр-поршень с начальным объемом 0.3, содержащий 5 кг газообразного метана при давлении 200 кПа. Газ сжимают политропно (n = 1.32) до давления 1 МПа и объема 0.005. Рассчитайте теплопередачу во время процесса.
- 6. Примите во внимание цилиндр-поршень, содержащий 1 кг метана при 500 кПа, 20 ° C. Газ политропно сжимают до давления 800 кПа. Рассчитайте теплопередачу с показателем n = 1.15.
- 7. 1 кг гелия хранится в системе поршень-цилиндр при 303 К, 200 кПа сжимается до 400 К в обратимом политропном процессе с показателем степени n = 1.24. Гелий является идеальным газом, поэтому удельная теплоемкость будет фиксированной. Найдите работу и теплопередачу.
- 8. Предположите, что воздух хранится в баллоне объемом 0.3 литра при 3 МПа, 2000 К. Воздух расширяется в соответствии с обратимым политропным процессом с показателем степени n = 1.7, объемное соотношение в этом случае составляет 8: 1. Рассчитайте политропную работу для процесса и сравните ее с адиабатической работой, если процесс расширения следует за обратимым адиабатическим расширением.
- 9. В закрытом контейнере содержится 200 л газа при 35 ° C, 120 кПа. Газ сжимается в политропном процессе до температуры 200 ° C, 800 кПа. Найти политропную работу, совершаемую воздухом для n = 1.29.
- 10. Масса 12 кг газообразного метана при 150 ° C, 700 кПа подвергается политропному расширению с n = 1.1 до конечной температуры 30 ° C. Найти теплопередачу?
- 11. Узел цилиндр-поршень содержит R-134a при 10 ° C; объем 5 литров. Охлаждающая жидкость сжимается до 100 ° C, 3 МПа в соответствии с обратимым политропным процессом. рассчитать проделанную работу и теплоотдачу?
- 12. Является ли политропный процесс изотермическим по своей природе?
- 13. Обратим ли политропный процесс?
- 14. Адиабатический политропный процесс?
- 14. Что такое политропная эффективность?
- 15. Что такое гамма в политропном процессе?
- 16. что такое политропный процесс?
- 17. Какие выводы можно сделать для политропного процесса с n = 1?
- 18. Что такое неполитропный процесс?
- 21. В политропном процессе, когда PV n = константа, температура тоже постоянна?
- Политропический процесс
- Что такое политропический процесс
- Уравнение политропы для идеального газа
- Готовые работы на аналогичную тему
Видео:О.Я. Савченко 5.6.28* | Вывод уравнения политропыСкачать

Политропный процесс | 20+ важных часто задаваемых вопросов и числовых значений
Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Content
Видео:30. Политропические процессыСкачать

Политропный процесс
Видео:Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать

Определение политропный процесс
Видео:Термодинамика Л3.1. Политропический процесс. Термодинамические циклы и КПДСкачать

Политропное уравнение | Политропное уравнение состояния
Политропный процесс можно определить уравнением
показатель степени n называется индексом политропы. Он зависит от материала и варьируется от 1.0 до 1.4. Это метод постоянной удельной теплоемкости, при котором учитывается поглощение тепла газом из-за повышения температуры на единицу.
Видео:Идеальный газ в молекулярно-кинетической теории | Физика 10 класс #28 | ИнфоурокСкачать

Политропный индекс
- п nd закон термодинамики. Эти частные случаи используются в тепловом взаимодействии для астрофизики и химической энергии.
- п = 0: Р = С: Представляет собой изобарический процесс или процесс постоянного давления.
- n = 1: PV = C: Согласно предположению об идеальном газовом законе, PV = C представляет постоянную температуру или изотермический процесс.
- 1 0). Как и в циклах сжатия пара, тепло теряется в горячее окружение.
- п = γ: В предположении закона идеального газа, представляет собой постоянную энтропию, изэнтропический процесс или обратимый адиабатический процесс.
- γ
………………………. Связь между объемом [В] и температурой [Т]
………………………. Связь между давлением [P] и температурой [T]
Видео:Урок 172. Применение 1 закона термодинамики для различных процессовСкачать

Политропные работы
Уравнение идеального газа для политропного процесса дается формулой
Видео:Физика. Термодинамика: Адиабатный процесс. Центр онлайн-обучения «Фоксфорд»Скачать

Политропная теплопередача
По данным 1 st закон термодинамики,
Видео:Политропный процессСкачать

Политропный против изэнтропического процесса
Политропный процесс — это термодинамический процесс, который подчиняется уравнению
Этот процесс учитывает потери на трение и фактор необратимости процесса. Это реальный процесс, за которым следует газ в определенных условиях.
Изэнтропический процесс, также известный как обратимый адиабатический процесс, представляет собой идеальный процесс, в котором не происходит передача энергии или тепла через границы системы. В этом процессе предполагается, что система имеет изолированную границу. Т.к. теплопередача равна нулю. дQ = 0
Согласно первому закону термодинамика,
Видео:Уравнение состояния идеального газа. Практическая часть. 10 класс.Скачать

Политропный процесс против адиабатического процесса
Политропный процесс — это термодинамический процесс, который подчиняется уравнению
Этот процесс учитывает потери на трение и фактор необратимости процесса. Это реальный процесс, за которым следует газ в определенных условиях.
Адиабатический процесс — это особое и специфическое состояние политропного процесса, при котором.
Подобно изэнтропическому процессу, в этом процессе также не происходит передачи энергии или тепла через границы системы. В этом процессе предполагается, что система имеет изолированную границу.
Видео:Физика 10 класс (Урок№23 - Внутренняя энергия. Работа. Количество теплоты.)Скачать

Политропная эффективность
«Политропический КПД, точно определяемый как отношение идеальной работы сжатия для изменения перепада давления в многоступенчатом компрессоре к фактической работе сжатия при изменении перепада давления в многоступенчатом компрессоре».
Проще говоря, это изоэнтропическая эффективность процесса для бесконечно малой ступени многоступенчатого компрессора.
Где, γ = индекс адиабаты
Pd = Давление нагнетания
Ps = Давление всасывания
Td = Температура подачи
Видео:Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. Практическая часть.10 классСкачать

Политропная голова
Политропный напор можно определить как напор, создаваемый центробежным компрессором при политропном сжатии газа или воздуха. Величина развиваемого давления зависит от плотности сжатого газа, и это зависит от изменения плотности газа.
γ = индекс адиабаты
zсредний = Средний коэффициент сжимаемости
η = политропная эффективность
Pd = Давление нагнетания
Ps = Давление всасывания
S = удельный вес газа
Ts = Температура всасывания
Видео:Урок 157. Изопроцессы и их графики. Частные газовые законыСкачать

Политропный процесс для воздуха | Политропный процесс для идеального газа
Считается, что воздух является идеальным газом, и поэтому законы идеального газа применимы к воздуху.
………………………. Соотношение между давлением [P] и объемом [V]
………………………. Связь между объемом [В] и температурой [Т]
………………………. Связь между давлением [P] и температурой [T]
Видео:Связь между давлением, объёмом и температурой газаСкачать

Примеры политропных процессов
Видео:Уравнение идеального газа: PV = nRT | Газы.Молекулярно-кинетическая теория | Химия (видео 1)Скачать

1. Рассмотрим политропный процесс с индексом политропы. п = (1.1). Начальные условия: P1 = 0, В1 = 0 и заканчивается на P2= 600 кПа, В2 = 0.01 м 3 . Оцените проделанную работу и теплоотдачу.
Ответ: Работы, выполненные политропным процессом, предоставлены
Теплопередача определяется выражением
Видео:Физика. Термодинамика: Внутренняя энергия идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

2. Поршневой цилиндр содержит кислород при 200 кПа объемом 0.1 м. 3 и при 200 ° С. Масса добавляется так, чтобы газ сжимался с PV. 1.2 = постоянная до конечной температуры 400 ° C. Подсчитайте проделанную работу.
Ответ: Выполненная политропная работа определяется
Видео:Зависимость электрического сопротивления металлов от температуры. Сверхпроводимость. 8 класс.Скачать

3. Рассмотрим аргон при 600 кПа, 30 ° C, сжатый до 90 ° C в политропном процессе с n = 1.33. Найдите проделанную работу на Газе.
Ответ: Выполненная политропная работа определяется
для аргона при 30 ° C составляет 208.1 Дж / кг. K
Принимая m = 1 кг
Видео:Выпуск 78. Политропный процесс. Решение задач по термодинамике.Скачать

4. Предположим, что масса 10 кг ксенона хранится в баллоне при 500 К, 2 МПа, расширение представляет собой политропный процесс (n = 1.28) с конечным давлением 100 кПа. Посчитайте проделанную работу. Учтите, что система имеет постоянную удельную теплоемкость.
Ответ: Выполненная политропная работа определяется
для ксенона при 30 ° C — 63.33 Дж / кг. K
Принимая m = 10 кг
Видео:62. Уравнение Клапейрона-МенделееваСкачать

5. Рассмотрим цилиндр-поршень с начальным объемом 0.3, содержащий 5 кг газообразного метана при давлении 200 кПа. Газ сжимают политропно (n = 1.32) до давления 1 МПа и объема 0.005. Рассчитайте теплопередачу во время процесса.
Ответ: политропный Теплопередача дан кем-то
Видео:Термодинамика - Решение задач - Работа идеального газа в циклеСкачать
6. Примите во внимание цилиндр-поршень, содержащий 1 кг метана при 500 кПа, 20 ° C. Газ политропно сжимают до давления 800 кПа. Рассчитайте теплопередачу с показателем n = 1.15.
Ответ: Политропная теплопередача определяется
Мы знаем, что R для метана = 518.2 Дж / кг. K
7. 1 кг гелия хранится в системе поршень-цилиндр при 303 К, 200 кПа сжимается до 400 К в обратимом политропном процессе с показателем степени n = 1.24. Гелий является идеальным газом, поэтому удельная теплоемкость будет фиксированной. Найдите работу и теплопередачу.
Ответ: Выполненная политропная работа определяется
R для гелия составляет 2077.1 Дж / кг.
Политропная теплопередача определяется выражением
8. Предположите, что воздух хранится в баллоне объемом 0.3 литра при 3 МПа, 2000 К. Воздух расширяется в соответствии с обратимым политропным процессом с показателем степени n = 1.7, объемное соотношение в этом случае составляет 8: 1. Рассчитайте политропную работу для процесса и сравните ее с адиабатической работой, если процесс расширения следует за обратимым адиабатическим расширением.
Ответ: Нам дается
Соотношение между давлением [P] и объемом [V]
Выполненная политропная работа определяется выражением
Проделанная адиабатическая работа определяется выражением
Для процесса расширения Работа, выполняемая посредством обратимого адиабатического процесса, больше, чем Работа, выполняемая посредством обратимого политропного процесса.
9. В закрытом контейнере содержится 200 л газа при 35 ° C, 120 кПа. Газ сжимается в политропном процессе до температуры 200 ° C, 800 кПа. Найти политропную работу, совершаемую воздухом для n = 1.29.
Ответ: соотношение между давлением [P] и объемом [V]
Выполненная политропная работа определяется выражением
10. Масса 12 кг газообразного метана при 150 ° C, 700 кПа подвергается политропному расширению с n = 1.1 до конечной температуры 30 ° C. Найти теплопередачу?
Ответ: Мы знаем, что R для метана = 518.2 Дж / кг. K
Политропная теплопередача определяется выражением
11. Узел цилиндр-поршень содержит R-134a при 10 ° C; объем 5 литров. Охлаждающая жидкость сжимается до 100 ° C, 3 МПа в соответствии с обратимым политропным процессом. рассчитать проделанную работу и теплоотдачу?
Ответ: Мы знаем, что R для R-134a = 81.49 Дж / кг. K
Выполненная политропная работа определяется выражением
Политропная теплопередача определяется выражением
12. Является ли политропный процесс изотермическим по своей природе?
Ответ: Когда n становится 1 для политропного процесса: согласно предположению об идеальном газовом законе, PV = C представляет постоянную температуру или изотермический процесс.
13. Обратим ли политропный процесс?
Ответ: политропные процессы внутренне обратимы. Вот несколько примеров:
п = 0: Р = С: Представляет собой изобарический процесс или процесс постоянного давления.
n = 1: PV = C: Согласно предположению об идеальном газовом законе, PV γ = C представляет постоянную температуру или Изотермический процесс.
п = γ: В предположении закона идеального газа, представляет собой постоянную энтропию, изэнтропический процесс или обратимый адиабатический процесс.
n = Бесконечность: Представляет собой изохорный процесс или процесс постоянного объема.
14. Адиабатический политропный процесс?
Ответ: когда п = γ: В предположении закона идеального газа PV γ = C, представляет постоянную энтропию или изэнтропический процесс или обратимый адиабатический процесс.
14. Что такое политропная эффективность?
Ответ: Политропический КПД можно определить как отношение идеальной работы сжатия к фактической работе сжатия при изменении перепада давления в многоступенчатом компрессоре. Проще говоря, это изоэнтропическая эффективность процесса для бесконечно малой ступени многоступенчатого компрессора.
Проще говоря, это изоэнтропическая эффективность процесса для бесконечно малой ступени многоступенчатого компрессора.
Где, γ = индекс адиабаты
Pd = Давление нагнетания
Ps = Давление всасывания
Td = Температура подачи
Ts = Температура всасывания
15. Что такое гамма в политропном процессе?
Ответ: В политропном процессе, когда п = γ: В предположении закона идеального газа PV γ = C, представляет постоянную энтропию или изэнтропический процесс или обратимый адиабатический процесс.
16. что такое политропный процесс?
Ответ: Политропный процесс можно определить уравнением
показатель степени n называется индексом политропы. Он зависит от материала и варьируется от 1.0 до 1.4. Его также называют процессом с постоянной удельной теплотой, при котором тепло, поглощаемое газом, учитываемое из-за повышения температуры на единицу, является постоянным.
17. Какие выводы можно сделать для политропного процесса с n = 1?
Ответ: когда п = 1: PV n = C : Согласно предположению об идеальном газе, закон становится PV = C представляет собой постоянную температуру или изотермический процесс.
18. Что такое неполитропный процесс?
Ответ: Политропный процесс можно определить уравнением PV n = C показатель степени n называется индексом политропы. Когда,
- п 0). Как и в циклах сжатия пара, тепло теряется в горячее окружение.
- п = γ: В предположении закона идеального газа PV γ = C представляет постоянную энтропию или изэнтропический процесс или обратимый адиабатический процесс.
- γn
После появления γ n 0). Как и в циклах сжатия пара, тепло теряется в горячее окружение. Изменение температуры происходит из-за изменения внутренней энергии, а не подводимого тепла. Произведенная работа превышает количество поданного или добавленного тепла. Таким образом, даже если при политропном расширении добавляется тепло, температура газа снижается.
21. В политропном процессе, когда PV n = константа, температура тоже постоянна?
Ответ: В политропном процессе, когда PV n = постоянная, температура остается постоянной только при показателе политропы n = 1. Для n = 1: PV = C: Согласно предположению об идеальном газовом законе, PV = C представляет постоянную температуру или изотермический процесс.
Чтобы узнать о просто поддерживаемой балке (нажмите сюда)и консольная балка (Кликните сюда)
О Хакимуддине Бавангаонвале

Подключитесь в LinkedIn — https://www.linkedin.com/in/hakimuddin-bawangaonwala
Политропический процесс
Вы будете перенаправлены на Автор24
Что такое политропический процесс
Политропическим или политропным процессом называют процесс, который происходит при неизменной теплоемкости. Все уравнения изо процессов и адиабатный процесс можно легко получить изменяя показатель политропы. Так, при изохорном процессе молярная теплоемкость равна $_)$:
При изобарном ($c_$):
При изотермическом процессе теплоемкость равна $pm infty $. При адиабатическом процессе теплоемкость равна нулю.
Уравнение политропы для идеального газа
Получим уравнение политропы для идеального газа, следуя тому, что теплоемкость должна быть постоянна.
Из уравнения Менделеева — Клайперона для идеального газа:
Из соотношения Майера:
[C_p-C_V=nu R left(5right).]
Подставим (5) в (4), получим:
Разделим уравнение (3) $T $, получим:
Очевидно, что если теплоемкость процесса постоянная, то
Уравнение интегрируем, потенцируем, получаем:
Уравнение (8) — уравнение политропы в переменных T, V. Используя уравнение Менделеева — Клайперона легко получить политропу в параметрах $p,V$ или $p,T$.
При $С=0$, $n=𝛾$. При $C=infty , n=1$ получаем уравнение Бойля — Мариотта ($T=const$). При С=$C_p$, n=0 — уравнение для $p=const$, при С=$C_V, n=pm infty $- уравнение для $V=const$.
Задание: Идеальный газ совершает политропный процесс. Найти молярную теплоемкость в этом процессе $с_$, если $i$ — число степеней свободы для этого газа.
Запишем первое начало термодинамики:
[CdT=fracnu RdT+pdV left(1.1right).]
Разделим уравнение на $dT$, получим:
Запишем уравнение процесса:
Используем уравнение Менделеева — Клайперона:
Подставим в (1.2) результаты преобразований (1.4) и (1.5), получим:
Ответ: Выражение для молярной теплоемкости в политропном процессе: $с_$=$frac+frac$.
Готовые работы на аналогичную тему
Задание: Можно ли вычислить работу газа по формуле:
для адиабатного, изотермического и изобарного процессов?
Основанием для решения задачи является уравнение политропы в параметрах $p,V$ (можно и в других):
Все перечисленные в условиях задачи процессы являются частными случаями политропического процесса. Рассмотрим адиабатный процесс. Для него $n=gamma$. Подставим показатель адиабаты в (2.1) вместо n, получим:
Сравним с уравнением работы для адиабатного процесса, которое было рассмотрено в разделе, посвященном этому процессу, имеем:
Если учесть, что из уравнения Менделеева-Клайперона:
то получаем, что выражения (2.3) и (2.4) эквивалентны.
Рассмотрим изотермический процесс. Для него $n=1$, соответственно, уравнение политропы имеет вид:
Уравнение (2.6) известный закон Бойля — Мариотта. Подставим $n=1$ в (2.1), получим:
Мы получили, что работа стремится к $infty $. Следовательно, приведенная формула (2.1) для вычисления работы в изотермическом процессе не подходит.
Рассмотри изобарный процесс. Для него $n=0$. Уравнение политропы примет вид:
[pV^0=const to p=const left(2.8right).]
Подставим $n=0$ в выражение для работы (2.1), получим:
Выражение (2.9) соответствует формуле вычисления работы для изобарного процесса.
Ответ: Данная формула подходит для вычисления работы в процессах: адиабатном и изобарном, не подходит для вычисления работы в изотермическом процессе.
Задание: Газ участвует в политропическом процессе. Пусть уравнение процесса задано в параметрах $p,V$ при каких значениях $n$
- Температура растет при расширении газа?
- Температура падает при увеличении объема?
- T=const при увеличении объема?
Уравнение политропы имеет вид:
Рассматривая уравнение (3.1), сразу можно дать ответ на третий вопрос: температура постоянна при n=0, так как в таком случае мы получаем закон Бойля — Мариотта:
Если перейти от (3.1) в уравнение политропы в параметрах T, V, то ответим и на два первых вопроса. Для перехода используем уравнение Менделеева — Клайперона (возьмем его для одного моля, что не нарушит общности рассуждений):
Подставим (3.3) вместо p (3.2), получим:
Для того, чтобы определить, что происходит с температурой согласно уравнению (3.4), необходимо сравнить $1-n$ с нулем. Если $1-n>0$, то с ростом $V$ растет и $T$. И наоборот.
- $1-n>0, to n
- $1-n1$ при таком n, если $Vuparrow , то Tdownarrow$.
Ответ: Температура растет при расширении газа если $n1$. $T=const$ при увеличении объема, если $n=0$.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 26.11.2021