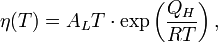Вывод уравнения лапласа для давления

Видео:Смачивание. Капиллярные явления. 10 класс.Скачать

Вывод уравнения лапласа для давления

Форма поверхности жидкости, налитой в сосуд, определяется тремя факторами: силами взаимодействия между молекулами жидкости, силами взаимодействия между молекулами жидкости и молекулами, входящими в состав стенок сосуда, и действием силы тяжести.

Если достаточно большое количество жидкости налито в широкий сосуд, то жидкость вследствие преобладающего действия силы тяжести в этом случае имеет плоскую горизонтальную поверхность. Однако непосредственно у стенок сосуда поверхность жидкости несколько искривлена. Если молекулы жидкости, соприкасающиеся со стенкой сосуда, взаимодействуют с молекулами твердого тела сильнее, чем между собой, в этом случае жидкость стремится увеличить площадь соприкосновения с твердым телом. При этом поверхность жидкости изгибается вниз и говорят, что она смачивает стенки сосуда, в котором находится.

Если же молекулы жидкости взаимодействуют между собой сильнее, чем с молекулами стенок сосуда, то жидкость стремится сократить площадь соприкосновения с твердым телом, ее поверхность искривляется вверх, имеет место несмачивание жидкостью стенок сосуда.

Рис. 1

В узких трубочках, диаметр которых составляет доли миллиметра, искривленные края жидкости охватывают весь поверхностный слой, и вся поверхность жидкости в таких трубочках имеет вид, напоминающий полусферу. Это так называемый мениск. Он может быть вогнутым, как на рис. 1 а, в случае смачивания, и выпуклым, как на рис. 1 б, при несмачивании. Радиус кривизны поверхности жидкости при этом того же порядка, что и радиус трубки. Явления смачивания и несмачивания характеризуются краевым углом θ между смоченной поверхностью твердого тела и мениском в точках их соприкосновения (рис.1 а, б).

Наличие сил поверхностного натяжения и кривизны поверхности жидкости в капиллярной трубочке ответственно за дополнительное давление под искривленной поверхностью, называемое давлением Лапласа.

Рис. 2

Для вывода формулы, определяющей величину давления Лапласа, рассмотрим случай, когда поверхность жидкости в сосуде принимает форму выпуклого мениска (рис. 2). Пусть – сила поверхностного натяжения, действующая по касательной к поверхности жидкости, R – радиус кривизны поверхности мениска, r – радиус кривизны сечения мениска горизонтальной плоскостью. Силу можно разложить на две составляющие и . Очевидно, что при суммировании по периметру мениска все составляющие дадут ноль, и давление Лапласа будет обусловлено суммарным действием составляющих . Найдем составляющую и проведем суммирование по контуру, ограничивающему мениск в горизонтальном сечении, имея в виду, что сила поверхностного натяжения , где Δl – элемент длины контура.

,

(6.17)

.

(6.18)

.

,

Рис. 3

Радиусы кривизны, входящие в последнюю формулу, являются алгебраическими величинами. Если центр кривизны нормального сечения мениска находится под его поверхностью, то соответствующий радиус кривизны является положительной величиной (рис. 3 а). В случае, когда центр кривизны находится над поверхностью мениска, R – отрицательно (рис. 3 б). Отсюда следует, что под выпуклой поверхностью мениска давление Лапласа положительно (оно добавляется к атмосферному давлению Р₀), под вогнутой поверхностью мениска давление Лапласа отрицательно (оно меньше атмосферного давления Р₀ на величину Р_Л). Очевидно, что давление Лапласа тем больше, чем меньше радиус кривизны сечения, поэтому оно играет наиболее важную роль в капиллярных явлениях.

Применяя формулу Лапласа для частного случая сферической капли , находим:

.

Если поверхность мениска имеет цилиндрическую форму, то один из радиусов кривизны сечения можно считать равным бесконечности. Для этого частного случая давление Лапласа равно

.

В случае мыльного пузырька дополнительное давление, которое испытывает находящийся внутри него газ, равно , так как у пузырька две поверхности – наружная и внутренняя, каждая из которых создает дополнительное давление Лапласа.

Видео:Сопротивление материалов. Лекция: тонкостенные оболочки вращения (исправленное видео)Скачать

Закон Лапласа

Капиллярным давлением называют разность давлений, возникающую вследствие искривления поверхности жидкости. Такую поверхность имеют, например, капли в эмульсиях и туманах, капиллярные мениски. Обозначим давление под искривлённой поверхностью жидкости — pr, давление под плоской поверхностью — p0.

Капиллярное давление определяется уравнением:

Знак капиллярного давления зависит от знака кривизны. Выпуклые поверхности имеют положительную кривизну. Центр кривизны выпуклой поверхности находится внутри соответствующей фазы. Тогда согласно уравнению капиллярное давление pc>0, то есть давление под выпуклой поверхностью жидкости больше, чем давление под плоской поверхностью: pr>p0. Пример дисперсной частицы с выпуклой поверхностью — капля жидкости в аэрозоле или эмульсии. Выпуклую поверхность имеет мениск несмачивающей жидкости в капилляре.

Вогнутые поверхности имеют отрицательную кривизну, поэтому капиллярное давление pc > b. Для нанообъектов это условие не выполняется, так как радиус кривизны соизмерим с молекулярными размерами.

Закон капиллярного давления имеет большое научное значение. Он устанавливает фундаментальное положение о зависимости физического свойства от геометрии, а именно от кривизны поверхности жидкости. Теория Лапласа оказала значительное влияние на развитие физикохимии капиллярных явлений, а также на некоторые другие дисциплины. Например, математическое описание искривлённых поверхностей было выполнено К. Гауссом именно в связи с капиллярными явлениями.

Закон Лапласа имеет много практических приложений в химической технологии, фильтрации, течении двухфазных потоков и т. д. Уравнение капиллярного давления используют во многих методах измерения поверхностного натяжения жидкостей. Закон Лапласа часто называют первым законом капиллярности.

Видео:Урок 202. Давление под искривленной поверхностью жидкости. Формула ЛапласаСкачать

Давление под искривленной поверхностью жидкости

Жидкости

Если поверхность жидкости не плоская, а искривленная, то она оказывает на жидкость избыточное (добавочное) давление. Это давление, обусловленное силами поверхностного натяжения, для выпуклой поверхности положительно, а для вогнутой поверхности — отрицательно.

Для расчета избыточного давления предположим, что свободная поверхность жидкости имеет форму сферы радиуса R, от которой мысленно отсечен шаровой сегмент, опирающийся на окружность радиуса г = Rsina (рис. 100). На каждый бесконечно малый элемент длины Dl этого контура действует сила поверхностного натяжения DF = sDl, касательная к поверхности сферы.

Разложив DF на два компонента (DF1 и DF2), видим, что геометрическая сумма сил DF2 равна нулю, так как эти силы на противоположных сторонах контура направлены в обратные стороны и взаимно уравновешиваются.

Поэтому равнодействующая сил поверхностного натяжения, действующих на вырезанный сегмент, направлена перпендикулярно плоскости сечения внутрь жидкости и равна алгебраической сумме составляющих DF1:

Разделив эту силу на площадь основания сегмента яг2, вычислим избыточное давление на жидкость, создаваемое силами поверхностного натяжения и обусловленное кривизной поверхности:

Если поверхность жидкости вогнутая, то можно доказать, что результирующая сила поверхностного натяжения направлена из жидкости и равна

Следовательно, давление внутри жидкости под вогнутой поверхностью меньше, чем в газе, на величину Dp.

Формулы (68.1) и (68.2) являются частным случаем формулы Лапласа*, определяющей избыточное давление для произвольной поверхности жидкости двоякое кривизны:

где R1и R2 — радиусы кривизны двух любых взаимно перпендикулярных нормальных сечений поверхности жидкости в данной точке. Радиус кривизны положителен, если центр кривизны соответствующего сечения находится внутри жидкости, и отрицателен, если центр кривизны находится вне жидкости.

Для сферической искривленной поверхности (R1 = R1 = R)выражение (68.3) переходит в (68.1), для цилиндрической (R1 = Rи R2 = ¥) — избыточное давление

В случае плоской поверхности (R1 = R2 = ¥)силы поверхностного натяжения избыточного давления не создают.

Капиллярныe явления

Если поместить узкую трубку (капилляр) одним концом в жидкость, налитую в широкий сосуд, то вследствие смачивания или несмачивания жидкостью стенок капилляра кривизна поверхности жидкости в капилляре становится значительной. Если жидкость смачивает материал трубки, то внутри ее поверхность жидкости — мениск — имеет вогнутую форму, если не смачивает — выпуклую (рис. 101).

Под вогнутой поверхностью жидкости появится отрицательное избыточное давление, определяемое по формуле (68.2). Наличие этого давления приводит к тому, что жидкость в капилляре поднимается, так как под плоской поверхностью жидкости в широком сосуде избыточного давления нет.

Если же жидкость не смачивает стенки капилляра, то положительное избыточное давление приведет к опусканию жидкости в капилляре. Явление изменения высоты уровня жидкости в капиллярах называется капиллярностью.

Жидкость в капилляре поднимается или опускается на такую высоту h, при которой давление столба жидкости (гидростатическое давление) rghуравновешивается избыточным давлением Dр, т. е.

где р — плотность жидкости, g — ускорение свободного падения.

Если r— радиус капилляра, q— краевой угол, то из рис. 101 следует, что (2scosq)/r = rgh, откуда

В соответствии с тем, что смачивающая жидкость по капилляру поднимается, а несмачивающая — опускается, из формулы (69.1) при q 0) получим положительные значения А, а при 0>я/2 (cos0

Видео:7.1 Решение уравнения Лапласа в прямоугольникеСкачать

Давление под искривленной поверхностью жидкости

Если поверхность жидкости не плоская, а искривленная, то она оказывает на жидкость избыточное (добавочное) давление. Это давление, обусловленное силами поверхностного натяжения, для выпуклой поверхности положительно, а для вогнутой поверхности — отрицательно.

Для расчета избыточного давления предположим, что свободная поверхность жидкости имеет форму сферы радиуса R, от которой мысленно отсечен шаровой сегмент, опирающийся на окружность радиуса r=Rsina (рис. 100).

На каждый бес­конечно малый элемент длины Dl этого контура действует сила поверхностного натяжения DF = s Dl, касательная к поверхности сферы.

Разложив DF на два компонента (DF1 и DF2), видим, что геометрическая сумма сил DF2 равна нулю, так как эти силы на противоположных сторонах контура направлены в обратные стороны и взаимно уравновешиваются.

Поэтому равнодействующая сил поверхностного натяжения, дей­ствующих на вырезанный сегмент, направлена перпендикулярно плоскости сечения внутрь жидкости и равна алгебраической сумме составляющих DF1:

Разделив эту силу на площадь основания сегмента pr2, вычислим избыточное давление на жидкость, создаваемое силами поверхностного натяжения и обусловленное кривиз­ной поверхности:

Если поверхность жидкости вогнутая, то можно доказать, что результирующая сила поверхностного натяжения направлена из жидкости и равна

Следовательно, давление внутри жидкости под вогнутой поверхностью меньше, чем в газе, на величину Dp.

Формулы (68.1) и (68.2) являются частным случаем формулы Лапласа,* определяющей избыточное давление для произвольной поверхности жидкости двоякой кривизны:

где R1 и R2 — радиусы кривизны двух любых взаимно перпендикулярных нормальных сечений поверхности жидкости в данной точке. Радиус кривизны положителен, если центр кривизны соответствующего сечения находится внутри жидкости, и отрицателен, если центр кривизны находится вне жидкости.

Для сферической искривленной поверхности (R1=R2=R) выражение (68.3) перехо­дит в (68.1),

для цилиндрической (R1=R и R2=¥) — избыточное давление

В случае плоской поверхности (R1=R2=¥) силы поверхностного натяжения избыточного давления не создают.

Капиллярные явления.

Если поместить узкую трубку(капилляр) одним концом в жидкость, налитую в широ­кий сосуд, то вследствие смачивания или не смачивания жидкостью стенок капилляра кривизна поверхности жидкости в капилляре становится значительной. Если жидкость смачивает материал трубки, то внутри ее поверхность жидкости —мениск — имеет вогнутую форму, если не смачивает — выпуклую (рис. 101).

Под вогнутой поверхностью жидкости появится отрицательное избыточное давление, определяемое по формуле (68.2). Наличие этого давления приводит к тому, что жидкость в капилляре поднимается, таккак под плоской поверхностью жидкости в широком сосуде избыточного давления нет.

Если же жидкость не смачивает стенки капилляра, то положительное избыточное давление приведет к опусканию жидкости в капилляре. Явление изменения высоты уровня жидкости в капиллярах называется капиллярностью.

Жидкость в капилляре поднимается или опускается на такую высоту h, при которой давление столба жидкости (гидростатическое давление) rgh уравновешивается избыточным давлением Dp, т. е.

где r — плотность жидкости, g — ускорение свободного падения.

Если r — радиус капилляра, q — краевой угол, то из рис. 101 следует, что (2s cosq)/r = rgh, откуда

В соответствии с тем, что смачивающая жидкость по капилляру поднимается, а не смачивающая — опускается, из формулы (69.1) при q0) получим положительные значения h, а при q>p/2 (cosq

Видео:Урок 203. Задачи на давление ЛапласаСкачать

Давление под искривленной поверхностью жидкости

Если поверхность жидкости не плоская, то стремление ее к сокращению приведет к возникновению давления, дополнительного к тому, которое испытывает жидкость с плоской поверхностью. В случае выпуклой поверхности это дополнительное давление положительно, в случае вогнутой поверхности — отрицательно.

Вычислим добавочное давление Dр для сферической поверхности жидкости (рис.9.13). Рассечем мысленно сферическую каплю жидкости диаметральной плоскостью на два полушария.

Из-за поверхностного натяжения оба полушария притягиваются с силой, равной

Кривизна сферической поверхности всюду одинакова и определяется радиусом сферы R. Чем меньше R, тем больше кривизна поверхности. Для сферической поверхности кривизна Н=1/R.

Если форма поверхности несферическая, то Dр выражается через среднюю кривизну нормального сечения. Нормальным сечением поверхности называется линия пересечения поверхности плоскостью, проходящей через нормаль в данной точке. В геометрии доказывается, что полусумма обратных радиусов кривизны:

для любой пары взаимно перпендикулярных нормальных сечений имеет одно и то же значение. Эта величина и есть средняя кривизна поверхности в данной точке.

Радиусы R1 и R2 в формуле (9.8.1) – алгебраические величины.

Если центр кривизны нормального сечения находится под данной поверхностью, соответствующий радиус кривизны положителен; если центр кривизны лежит над поверхностью, радиус кривизны отрицателен.

Неплоская поверхность может иметь среднюю кривизну, равную нулю. Для этого нужно, чтобы радиусы кривизны R1 и R2 были одинаковы по величине и противоположны по знаку.

Для сферы Н=1/R, поэтому

Лаплас доказал, что эта формула справедлива для поверхности любой формы, если под Н понимать среднюю кривизну поверхности в той точке, под которой определяется дополнительное давление. Подставив сюда выражение для средней кривизны, получим формулу для добавочного давления под произвольной поверхностью:

формула Лапласа.

Для сферической искривленной поверхности (R1=R2=R) это выражение переходит в , для цилиндрической (R1=R, R2=¥) – избыточное давление . В случае плоской поверхности (R1=R2=¥) силы поверхностного натяжения избыточного давления не создают. Добавочное давление обуславливает изменение уровня жидкости в узких трубках (капилляр), вследствие чего оно еще называется капиллярным давлением.

Капиллярность.

Изменение высоты уровня жидкости в узких трубках или зазорах получило название капиллярности. (Лат. capillus) означает волос. Капилляр – «трубка, тонкая, как волос»).

где R – радиус мениска. Выразим радиус мениска через краевой угол q и радиус капилляра r: . Тогда высота поднятия жидкости в капилляре:

Смачивающая жидкость (q0) поднимается по капилляру(рис.9.14 — вода), и эта формула дает положительное значение h, а несмачивающая жидкость (q>p/2, cos q

Видео:Межфазное натяжение, смачиваемость, капиллярное давлениеСкачать

Давление Лапласа — История развития коллоидной химии

Форма поверхности жидкости, налитой в сосуд, определяется тремя факторами: силами взаимодействия между молекулами жидкости, силами взаимодействия между молекулами жидкости и молекулами, входящими в состав стенок сосуда, и действием силы тяжести.

Если достаточно большое количество жидкости налито в широкий сосуд, то жидкость вследствие преобладающего действия силы тяжести в этом случае имеет плоскую горизонтальную поверхность. Однако непосредственно у стенок сосуда поверхность жидкости несколько искривлена.

Если молекулы жидкости, соприкасающиеся со стенкой сосуда, взаимодействуют с молекулами твердого тела сильнее, чем между собой, в этом случае жидкость стремится увеличить площадь соприкосновения с твердым телом.

При этом поверхность жидкости изгибается вниз и говорят, что она смачивает стенки сосуда, в котором находится.

Если же молекулы жидкости взаимодействуют между собой сильнее, чем с молекулами стенок сосуда, то жидкость стремится сократить площадь соприкосновения с твердым телом, ее поверхность искривляется вверх, имеет место несмачивание жидкостью стенок сосуда.

Рис. 1

В узких трубочках, диаметр которых составляет доли миллиметра, искривленные края жидкости охватывают весь поверхностный слой, и вся поверхность жидкости в таких трубочках имеет вид, напоминающий полусферу. Это так называемый мениск. Он может быть вогнутым, как на рис.

1 а, в случае смачивания, и выпуклым, как на рис. 1 б, при несмачивании. Радиус кривизны поверхности жидкости при этом того же порядка, что и радиус трубки.

Явления смачивания и несмачивания характеризуются краевым углом θ между смоченной поверхностью твердого тела и мениском в точках их соприкосновения (рис.1 а, б).

Наличие сил поверхностного натяжения и кривизны поверхности жидкости в капиллярной трубочке ответственно за дополнительное давление под искривленной поверхностью, называемое давлением Лапласа.

Рис. 2

Для вывода формулы, определяющей величину давления Лапласа, рассмотрим случай, когда поверхность жидкости в сосуде принимает форму выпуклого мениска (рис. 2). Пусть – сила поверхностного натяжения, действующая по касательной к поверхности жидкости, R – радиус кривизны поверхности мениска, r – радиус кривизны сечения мениска горизонтальной плоскостью. Силу можно разложить на две составляющие и . Очевидно, что при суммировании по периметру мениска все составляющие дадут ноль, и давление Лапласа будет обусловлено суммарным действием составляющих . Найдем составляющую и проведем суммирование по контуру, ограничивающему мениск в горизонтальном сечении, имея в виду, что сила поверхностного натяжения , где Δl – элемент длины контура.

Действие этой силы приходится на круговое сечение мениска площадью (рис. 2). Следовательно, избыточное давление Лапласа, обусловленное кривизной поверхности и действием сил поверхностного натяжения, равно

Можно обобщить полученную формулу на случай более сложной поверхности. В общем случае давление Лапласа определяется соотношением

где R1 и R2 – радиусы кривизны двух взаимно перпендикулярных сечений мениска.

Радиусы кривизны, входящие в последнюю формулу, являются алгебраическими величинами. Если центр кривизны нормального сечения мениска находится под его поверхностью, то соответствующий радиус кривизны является положительной величиной (рис. 3 а). В случае, когда центр кривизны находится над поверхностью мениска, R – отрицательно (рис. 3 б).

Отсюда следует, что под выпуклой поверхностью мениска давление Лапласа положительно (оно добавляется к атмосферному давлению Р0), под вогнутой поверхностью мениска давление Лапласа отрицательно (оно меньше атмосферного давления Р0 на величину РЛ).

Очевидно, что давление Лапласа тем больше, чем меньше радиус кривизны сечения, поэтому оно играет наиболее важную роль в капиллярных явлениях.

Применяя формулу Лапласа для частного случая сферической капли , находим:

Если поверхность мениска имеет цилиндрическую форму, то один из радиусов кривизны сечения можно считать равным бесконечности. Для этого частного случая давление Лапласа равно

В случае мыльного пузырька дополнительное давление, которое испытывает находящийся внутри него газ, равно , так как у пузырька две поверхности – наружная и внутренняя, каждая из которых создает дополнительное давление Лапласа.

1) http://ido.tsu.ru/schools/physmat/data/res/molek/uchpos/text/m6_09.htm2) Натяжение пленок и давление Лапласа под искривленнойповерхностью жидкости

Видео:Поверхностные явления. Давление ЛапласаСкачать

Капилляры

Если в жидкость опустить тонкую трубку, называемую капилляром, то уровень жидкости, вошедшей в трубку, не будет равен уровню жидкости вне трубки. При этом, чем более тонкую трубку мы возьмем, тем большую разность уровней будем иметь.

Одни жидкости по капиллярным трубкам поднимаются, другие в них опускаются.

Можно заметить, что те жидкости, которые по трубкам поднимаются, смачивают их поверхность, а те, что опускаются, не смачивают.

Cмачивающая поверхность капиллярной трубки жидкость образует вогнутый мениск, а несмачивающая – выпуклый. В тонких капиллярах искривленную поверхность жидкости можно принять за полусферу.

Попытаемся выяснить, как ведет себя жидкость, находящаяся под искривленной поверхностью. Для этого вспомним, что с искривленной поверхностью жидкости мы имеем дело не только в капиллярах. Например, сферическую поверхность имеет мыльный пузырь.

Выдуем мыльный пузырь и поднесем трубочку, из которой он выдувался, к пламени свечи. Пламя отклоняется в сторону, что свидетельствует о том, что из трубочки под давлением выходит воздух.

Определим, как зависит давление воздуха, находящегося внутри мыльного пузыря, от его диаметра. Для этого выдуем из двух трубочек, соединенных друг с другом, два мыльных пузыря неодинаковых размеров. Закроем отверстие, через которое мы надували пузыри. Размеры пузырей начинают изменяться так, что большой пузырь становится еще больше, а маленький еще меньше.

Таким образом, избыточное давление под искривленной поверхностью (по отношению к давлению под плоской поверхностью) оказывается обратно пропорциональным радиусу кривизны поверхности:

Таким образом, избыточное давление жидкости под искривленной поверхностью:

где k – постоянный коэффициент, не имеющий наименования.

Зная значения коэффициента поверхностного натяжения для различных жидкостей по результатам измерений уже известным нам методом отрыва проволочки от поверхности жидкости, плотности этих жидкостей, высоты их поднятия в капиллярах и радиусы соответствующих капилляров, можно найти значение коэффициента k в записанном уравнении. Он оказывается равным 2. С учетом этого, уравнение, показывающее зависимость избыточного давления под сферической поверхностью жидкости, принимает вид:

Формулу для расчета высоты поднятия или опускания жидкости в капилляре можно получить и другим способом.

Следует иметь в виду, что приводимые рассуждения относятся к случаю, когда мениск имеет сферическую форму. Для этого случая результирующая сил взаимодействия молекул жидкости, входящей в капилляр, и вещества из которого изготовлен капилляр, направлена или вертикально вверх, или вертикально вниз. Уровень жидкости в капилляре изменяется в том направлении, в каком действует сила.

Допустим, капилляр смачивается жидкостью, и она поднимается по нему. Подъем будет происходить до тех пор, пока сила поверхностного натяжения не уравновесится силой тяжести, действующей на жидкость.

Приравняв значения этих сил и произведя ряд математических преобразований, мы можем получить уравнение, показывающее, от каких величин зависит высота подъема жидкости в капилляре.

В частности, оказывается, что эта высота находится в обратной зависимости от радиуса капилляра.

То, что для данной жидкости высота ее поднятия по капиллярному сосуду находится в обратно пропорциональной зависимости от радиуса сосуда, хорошо иллюстрирует следующий опыт.

Возьмем две стеклянные пластинки и плотно прижмем их с одного края друг к другу. С другого края пластинки слегка разведем, вставив между ними тонкую прокладку.

После выполнения этих действий между пластинками образуется узкий клиновидный зазор. Слегка погрузим нижнюю кромку пластинок в кювету с водой.

Вода поднимается между пластинками так, что форма ее поверхности оказывается очень близкой к гиперболе.

Видео:Сопротивление материалов. Лекция: тонкостенные оболочки вращенияСкачать

§ 68. Давление под искривленной поверхностью жидкости

Если
поверхность жидкости не плоская, а
искривленная, то она оказывает на
жид­кость избыточное
(добавочное) давление. Это
давление, обусловленное силами
по­верхностного натяжения, для выпуклой
поверхности положительно, а для вогнутой
поверхности — отрицательно.

Для
расчета избыточного давления предположим,
что свободная поверхность жидкости
имеет форму сферы радиуса R,
от
которой мысленно отсечен шаровой
сег­мент, опирающийся на окружность
радиу­са r=Rsin
(рис.
100). На каждый бес­конечно малый элемент
длины l
этого контура действует сила поверхностного
натяжения F=l,
касательная к по­верхности сферы.

Разложив F
на
два компонента (F1
и
F2),
видим, что гео­метрическая сумма сил
F2
равна нулю, так как эти силы на
противоположных сторонах контура
направлены в обратные стороны и взаимно
уравновешиваются.

Поэтому равнодействующая
сил поверхно­стного натяжения,
действующих на вы­резанный сегмент,
направлена перпенди­кулярно плоскости
сечения внутрь жидко-

сти и равна алгебраической сумме со­ставляющих F1:

Разделив
эту силу на площадь основания сегмента
r2,
вычислим избыточное (до­бавочное)
давление на жидкость, создава­емое
силами поверхностного натяжения и
обусловленное кривизной поверхности:

Если поверхность
жидкости вогнутая, то можно доказать,
что результирующая сила поверхностного
натяжения направле­на из жидкости и
равна

Следовательно,
давление внутри жидкости под вогнутой
поверхностью меньше, чем в газе, на
величину р.

Формулы
(68.1) и (68.2) являются частным случаем
формулы
Лапласа,
оп­ределяющей
избыточное давление для произвольной
поверхности жидкости двоя­кой кривизны:

где
R1и
R2
— радиусы кривизны двух любых взаимно
перпендикулярных нор­мальных сечений
поверхности жидкости в данной точке.
Радиус кривизны положи­телен, если
центр кривизны соответствую­щего
сечения находится внутри жидкости, и
отрицателен, если центр кривизны
на­ходится вне жидкости.

Для
сферической искривленной повер­хности
(R1=R2=R)
выражение
(68.3) пе­реходит в (68.1), для цилиндрической
(R1=R
и
R2=)
— избыточное давление

Для
плоской поверхности (R1=R2=)
силы
поверхностного натяжения избыточ­ного
давления не создают.

§ 69. Капиллярные явления

Если
поместить узкую трубку (капилляр)
одним
концом в жидкость, налитую в ши­рокий
сосуд, то вследствие смачивания или
несмачивания жидкостью стенок ка­пилляра
кривизна поверхности жидкости в капилляре
становится значительной. Ес­ли жидкость
смачивает материал трубки, то внутри
ее поверхность жидкости — ме­ниск—
имеет вогнутую форму, если не смачивает
— выпуклую (рис. 101).

Под
вогнутой поверхностью жидкости появится
отрицательное избыточное дав­ление,
определяемое по формуле (68.2). Наличие
этого давления приводит к тому, что
жидкость в капилляре поднимается, так
как под плоской поверхностью жидко­сти
в широком сосуде избыточного давле­ния
нет.

Если же жидкость не смачивает стенки
капилляра, то положительное из­быточное
давление приведет к опусканию жидкости
в капилляре. Явление изменения высоты
уровня жидкости в капиллярах называется
капиллярностью.

Жидкость
в капилляре поднимается или опускается
на такую высоту h,
при
которой давление столба жидкости
(гидростатическое
дав­ление) gh
уравновешивается
избыточным давлением р,
т. е.

• 2/R=gh,
• где 
  — плотность жидкости, g
  —
  ускоре­ние свободного падения.
• Если
  m
  — радиус
  капилляра, 
  — крае­вой угол, то из рис. 101 следует,
  что (2cos)/r=gh,
  откуда

В соответствии с
тем, что смачиваю­щая жидкость по
капилляру поднимается, а несмачивающая
— опускается, из фор-

мулы
(69.1) при 0)
полу­чим положительные значения Л, а
при 0>/2
(cos

Видео:Вывод уравнения неразрывности - Лекция 1Скачать

КАПИЛЛЯ́РНЫЕ ЯВЛЕ́НИЯ

Авторы: А. М. Емельяненко, Н. В. Чураев

КАПИЛЛЯ́РНЫЕ ЯВЛЕ́НИЯ, со­во­куп­ность яв­ле­ний, обу­слов­лен­ных по­верх­но­ст­ным на­тя­же­ни­ем на гра­ни­це раз­де­ла не­сме­ши­ваю­щих­ся сред (в сис­те­мах жид­кость – жид­кость, жид­кость – газ или пар) при на­ли­чии ис­крив­ле­ния по­верх­но­сти. Ча­ст­ный слу­чай по­верх­но­ст­ных яв­ле­ний.

При от­сут­ст­вии си­лы тя­же­сти жид­кость ог­ра­ни­чен­ной мас­сы под воз­дей­ст­ви­ем по­верх­но­ст­но­го на­тя­же­ния стре­мит­ся за­нять объ­ём с ми­ним. по­верх­но­стью, т. е. при­ни­ма­ет фор­му ша­ра.

В ус­ло­ви­ях дей­ст­вия си­лы тя­же­сти не слиш­ком вяз­кая жид­кость дос­та­точ­ной мас­сы при­ни­ма­ет фор­му со­су­да, в ко­то­рый на­ли­та, и её сво­бод­ная по­верх­ность при от­но­си­тель­но боль­шой пло­ща­ди (вда­ли от сте­нок со­су­да) ста­но­вит­ся пло­ской, т. к. роль по­верх­но­ст­но­го на­тя­же­ния ме­нее су­ще­ст­вен­на, чем си­лы тя­же­сти.

При взаи­мо­дей­ст­вии с по­верх­но­стью др. жид­ко­сти или твёр­до­го те­ла (напр., со стен­ка­ми со­су­да) по­верх­ность рас­смат­ри­вае­мой жид­ко­сти ис­крив­ля­ет­ся в за­ви­си­мо­сти от на­ли­чия или от­сут­ст­вия сма­чи­ва­ния. Ес­ли име­ет ме­сто сма­чи­ва­ние, т. е. мо­ле­ку­лы жид­ко­сти 1 (рис.

1) силь­нее взаи­мо­дей­ст­ву­ют с мо­ле­ку­ла­ми по­верх­но­сти 3, чем с мо­ле­ку­ла­ми др. жид­ко­сти (или га­за) 2, то под воз­дей­ст­ви­ем раз­но­сти сил меж­мо­ле­ку­ляр­но­го взаи­мо­дей­ст­вия жид­кость 1 под­ни­ма­ет­ся по стен­ке со­су­да – уча­сток жид­ко­сти, при­мы­каю­щий к стен­ке, ис­крив­ля­ет­ся.

Дав­ле­ние, вы­зы­вае­мое подъ­ё­мом жид­ко­сти, урав­но­ве­ши­ва­ет­ся ка­пил­ляр­ным дав­ле­ни­ем $Delta p$ – раз­но­стью дав­ле­ний над и под ис­крив­лён­ной по­верх­но­стью раз­де­ла.

Ве­ли­чи­на ка­пил­ляр­но­го дав­ле­ния за­ви­сит от сред­не­го ра­диу­са $r$ кри­виз­ны по­верх­но­сти и оп­ре­де­ля­ет­ся фор­му­лой Ла­п­ла­са: $Delta p=2 sigma/r$, где $sigma$ – по­верх­но­ст­ное на­тя­же­ние. Ес­ли гра­ни­ца раз­де­ла фаз пло­ская ($r= infty$), то в ус­ло­ви­ях ме­ха­нич. рав­но­ве­сия сис­те­мы дав­ле­ния с обе­их сто­рон гра­ни­цы раз­де­ла рав­ны и $Delta p=0$. В слу­чае во­гну­той по­верх­но­сти жид­ко­сти ($r lt 0$) дав­ле­ние в жид­ко­сти ни­же, чем дав­ле­ние в гра­ни­ча­щей с ней фа­зе и $Delta p lt 0$; для вы­пук­лой по­верх­но­сти ($r>0$) $Delta p>0$.

Ес­ли стен­ки со­су­да при­бли­зить друг к дру­гу, зо­ны ис­крив­ле­ния по­верх­но­сти жид­ко­сти об­ра­зу­ют ме­ниск – пол­но­стью ис­крив­лён­ную по­верх­ность.

Об­ра­зо­вав­шая­ся сис­те­ма на­зы­ва­ет­ся ка­пил­ля­ром; в нём в ус­ло­ви­ях сма­чи­ва­ния дав­ле­ние под ме­ни­ском по­ни­же­но и жид­кость в ка­пил­ля­ре под­ни­ма­ет­ся (над уров­нем сво­бод­ной по­верх­но­сти жид­ко­сти в со­су­де); вес стол­ба жид­ко­сти вы­со­той $h$ урав­но­ве­ши­ва­ет ка­пил­ляр­ное дав­ле­ние $Delta p$.

Не­сма­чи­ваю­щая жид­кость в ка­пил­ля­ре об­ра­зу­ет вы­пук­лый ме­ниск, дав­ле­ние над ко­то­рым вы­ше, и жид­кость в нём опус­ка­ет­ся ни­же уров­ня сво­бод­ной по­верх­но­сти вне ка­пил­ля­ра.

Вы­со­та под­ня­тия (опус­ка­ния) жид­ко­сти в ка­пил­ля­ре от­но­си­тель­но сво­бод­ной по­верх­но­сти (где $r= infty$ и $Delta p=0$) оп­ре­де­ля­ет­ся со­от­но­ше­ни­ем: $h=2 sigma cos heta/ Delta
ho gr$, где $ heta$ – крае­вой угол (угол ме­ж­ду ка­са­тель­ной к по­верх­но­сти ме­ни­ска и стен­кой ка­пил­ля­ра), $Delta
ho$ – раз­ность плот­но­стей жид­ко­сти 1 в ка­пил­ля­ре и внеш­ней сре­ды 2, $g$ – ус­ко­ре­ние сво­бод­но­го па­де­ния.

Ис­крив­ле­ние по­верх­но­сти влия­ет на ус­ло­вия рав­но­ве­сия ме­ж­ду жид­ко­стью и её на­сы­щен­ным па­ром: со­глас­но Кель­ви­на урав­не­нию, дав­ле­ние па­ров над ка­п­лей жид­ко­сти по­вы­ша­ет­ся с умень­ше­ни­ем её ра­диу­са, что объ­яс­ня­ет, напр., рост боль­ших ка­пель в об­ла­ках за счёт ма­лых.

К ха­рак­тер­ным К. я. от­но­сят­ся ка­пил­ляр­ное впи­ты­ва­ние, по­яв­ле­ние и рас­про­стра­не­ние ка­пил­ляр­ных волн, ка­пил­ляр­ное пе­ре­дви­же­ние жид­ко­сти, ка­пил­ляр­ная кон­ден­са­ция, про­цес­сы ис­па­ре­ния и рас­тво­ре­ния при на­ли­чии ис­крив­лён­ной по­верх­но­сти.

Ка­пил­ляр­ное впи­ты­ва­ние ха­рак­те­ри­зу­ет­ся ско­ро­стью, за­ви­ся­щей от ка­пил­ляр­но­го дав­ле­ния и вяз­ко­сти жид­ко­сти. Оно иг­ра­ет су­ще­ст­вен­ную роль в во­до­снаб­же­нии рас­те­ний, дви­же­нии во­ды в поч­вах и др. про­цес­сах, свя­зан­ных с дви­же­ни­ем жид­ко­стей в по­рис­тых сре­дах.

Ка­пил­ляр­ная про­пит­ка – один из рас­про­стра­нён­ных про­цес­сов хи­мич. тех­но­ло­гии. В сис­те­мах с не­па­рал­лель­ны­ми стен­ка­ми (или ка­пил­ля­рах ко­нич.

се­че­ния) кри­виз­на ме­ни­сков за­ви­сит от рас­по­ло­же­ния в них гра­нич­ных по­верх­но­стей жид­ко­сти, и ка­п­ля сма­чи­ваю­щей жид­ко­сти в них на­чи­на­ет дви­гать­ся к ме­ни­ску с мень­шим ра­диу­сом (рис. 2), т. е. в ту сто­ро­ну, где дав­ле­ние ни­же.

При­чи­ной ка­пил­ляр­но­го пе­ре­дви­же­ния жид­ко­сти мо­жет слу­жить и раз­ни­ца сил по­верх­но­ст­но­го на­тя­же­ния в ме­ни­сках, напр. при су­ще­ст­во­ва­нии гра­ди­ен­та темп-ры или при ад­сорб­ции по­верх­но­ст­но-ак­тив­ных ве­ществ, сни­жаю­щих по­верх­но­ст­ное на­тя­же­ние.

Ка­пил­ляр­ной кон­ден­са­ци­ей на­зы­ва­ют про­цесс кон­ден­са­ции па­ра в ка­пил­ля­рах и мик­ро­тре­щи­нах по­рис­тых тел, а так­же в про­ме­жут­ках ме­ж­ду сбли­жен­ны­ми твёр­ды­ми час­ти­ца­ми или те­ла­ми.

Не­об­хо­ди­мое ус­ло­вие ка­пил­ляр­ной кон­ден­са­ции – на­ли­чие сма­чи­ва­ния по­верх­но­сти тел (час­тиц) кон­ден­си­рую­щей­ся жид­ко­стью.

Про­цес­су ка­пил­ляр­ной кон­ден­са­ции пред­ше­ст­ву­ет ад­сорб­ция мо­ле­кул па­ра по­верх­но­стью тел и об­ра­зо­ва­ние ме­ни­сков жид­ко­сти.

В ус­ло­ви­ях сма­чи­ва­ния фор­ма ме­ни­сков во­гну­тая и дав­ле­ние $p$ на­сы­щен­но­го па­ра над ни­ми ни­же, чем дав­ле­ние на­сы­щен­но­го па­ра $p_0$ при тех же ус­ло­ви­ях над пло­ской по­верх­но­стью. Т. е. ка­пил­ляр­ная кон­ден­са­ция про­ис­хо­дит при бо­лее низ­ких, чем $p_0$, дав­ле­ни­ях.

Ис­крив­ле­ние по­верх­но­сти жид­ко­сти мо­жет су­ще­ст­вен­но вли­ять на про­цес­сы ис­па­ре­ния, ки­пе­ния, рас­тво­ре­ния, за­ро­ды­ше­об­ра­зо­ва­ния при кон­ден­са­ции па­ра и кри­стал­ли­за­ции.

Так, свой­ст­ва сис­тем, со­дер­жа­щих боль­шое ко­ли­че­ст­во ка­пель или пу­зырь­ков га­за (эмуль­сий, аэ­ро­зо­лей, пен), и их фор­ми­ро­ва­ние во мно­гом оп­ре­де­ля­ют­ся К. я. Они ле­жат так­же в ос­но­ве мн. тех­но­ло­гич.

про­цес­сов: фло­та­ции, спе­ка­ния по­рош­ков, вы­тес­не­ния неф­ти из пла­стов вод­ны­ми рас­тво­ра­ми по­верх­но­ст­но-ак­тив­ных ве­ществ, ад­сорб­ци­он­но­го раз­де­ле­ния и очи­ст­ки га­зо­вых и жид­ких сме­сей и т. п.

Впер­вые К. я. бы­ли ис­сле­до­ва­ны Ле­о­нар­до да Вин­чи. Сис­те­ма­тич. на­блю­де­ния и опи­са­ния К. я.

в тон­ких труб­ках и ме­ж­ду пло­ски­ми, близ­ко рас­по­ло­жен­ны­ми стек­лян­ны­ми пла­сти­на­ми про­вёл в 1709 Ф. Хокс­би, де­мон­ст­ра­тор Лон­дон­ско­го ко­ро­лев­ско­го об-ва. Ос­но­вы тео­рии К. я.

за­ло­же­ны в тру­дах Т. Юн­га, П. Ла­п­ла­са, а их тер­мо­ди­на­мич. рас­смот­ре­ние осу­ще­ст­вил Дж. Гиббс (1876).

Видео:Метод Лапласа решения ДУСкачать

Давление под искривленной поверхностью жидкости

В случае если поверхность жидкости не плоская, а искривленная, то она оказывает на жидкость избыточное (добавочное) давление. Это давление, обусловленное силами поверхност­ного натяжения, для выпуклой поверхности положительно, а для вогнутой поверх­ности — отрицательно.

Для расчета избыточного давления предположим, что свободная поверхность жидкости имеет форму сферы радиуса R, от которой мысленно отсечен шаровой сегмент, опирающийся на окружность радиуса (ряс. 100). На каждый бес-

конечно малый элемент длины этого контура действует сала поверхностного натяжения касательная к поверхности сферы. Разложив на два компонента

видим, что геометрическая сумма сил равна нулю, так как эти силы на противоположных сторонах контура направлены в обратные стороны и взаимно уравновешиваются. По этой причине равнодействующая сил поверхностного натяжения, дей­ствующих на вырезанный сегмент, направлена перпендикулярно плоскости сечения внутрь жидкости и равна алгебраической сумме составляющих AF1:

Разделив эту силу на площадь основания сегмента пг2, вычислим избыточное давление на жидкость, создаваемое силами поверхностного натяжения и обусловленное кривиз­ной поверхности:

(68.1)

Давление под искривленной поверхностью жидкости — понятие и виды. Классификация и особенности категории «Давление под искривленной поверхностью жидкости» 2017, 2018.

🔥 Видео

Три давления? Нет, три энергии!Скачать

Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Физика. МКТ: Смеси газов. Закон Дальтона. Центр онлайн-обучения «Фоксфорд»Скачать

Капиллярный эффектСкачать

Гидростатическое давлениеСкачать

Уравнение ЛапласаСкачать

7.2 Уравнение Лапласа в секторе и кольцевом сектореСкачать

Оператор набла (оператор Гамильтона) и оператор ЛапласаСкачать

Уравнения математической физики. Уравнение Лапласа. Часть 1Скачать

Задача Дирихле для круга. Уравнение ЛапласаСкачать