Причина данной публикации — неоднозначная статья на тему принципа наименьшего действия (ПНД), опубликованная на ресурсе несколько дней назад. Неоднозначна она потому, что её автор в популярной форме пытается донести до читателя один из основополагающих принципов математического описания природы, и это частично ему удается. Если бы не одно но, притаившееся в конце публикации. Под спойлером приведена полная цитата данного отрывка
- Не все так просто
- 1. Определение действия по Гамильтону. Принцип наименьшего действия
- 2. Границы применимости принципа наименьшего действия. Некоторые определения для самых маленьких
- 3. Понятие о вариациях обобщенных координат. Постановка вариационной задачи
- 4. Решение вариационной задачи. Уравнения Лагранжа 2-го рода
- 5. Задача с шариком и стенкой
- Выводы и пожелания
- Вывод уравнения лагранжа из вариационного принципа
- 💥 Видео
Видео:№9. Элементы вариационного исчисления. Уравнения Лагранжа-Эйлера.Скачать

Не все так просто
На самом деле я немного обманул, сказав, что тела всегда двигаются так, чтобы минимизировать действие. Хотя в очень многих случаях это действительно так, можно придумать ситуации, в которых действие явно не минимально.
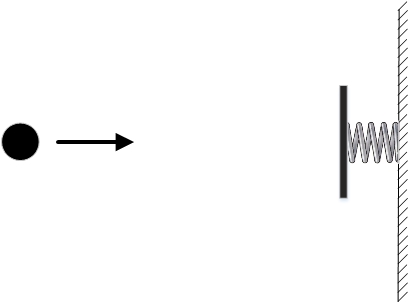
Например, возьмем шарик и поместим его в пустое пространство. На некотором отдалении от него поставим упругую стенку. Допустим, мы хотим, чтобы через некоторое время шарик оказался в том же самом месте. При таких заданных условиях шарик может двигаться двумя разными способами. Во-первых, он может просто оставаться на месте. Во-вторых, можно его толкнуть по направлению к стенке. Шарик долетит до стенки, отскочит от нее и вернется обратно. Понятно, что можно толкнуть его с такой скоростью, чтобы он вернулся в точно нужное время.
Оба варианта движения шарика возможны, но действие во втором случае получится больше, потому что все это время шарик будет двигаться с ненулевой кинетической энергией.
Как же спасти принцип наименьшего действия, чтобы он был справедлив и в таких ситуациях? Об этом мы поговорим в следующий раз.
Так в чем же, с моей точки зрения, проблема?
Проблема в том, что автор, приводя данный пример допустил ряд фундаментальных ошибок. Она усугубляется тем, что планируемая вторая часть, со слов автора, будет опираться на эти ошибки. Руководствуясь принципом наполнения ресурса достоверной информацией я вынужден выступить с разъяснением своей позиции по данному вопросу более развернуто, и формат комментариев для этого маловат.
Данная статья расскажет о том, как строится механика на базе ПНД, и постарается объяснить читателю, что проблема, которую ставит автор цитируемой публикации отсутствует.
Видео:Принцип наименьшего действия #2 - Уравнение Эйлера-ЛагранжаСкачать

1. Определение действия по Гамильтону. Принцип наименьшего действия
— функция Лагранжа, для некоторой механической системы, в которой (опуская аргументы в дальнейшем) T — кинетическая энергия системы; П — потенциальная её энергия; q(t) — вектор обобщенных координат этой системы, являющийся функцией времени. при этом полагают, что моменты времени t1 и t2 — фиксированы.
Почему функционал, а не функция? Потому, что функция, по определению есть правило, по которому одному числу из области определения (аргументу функции) ставится в соответствие другое число из области значений. Функционал отличается тем, что качестве его аргумента выступает не число, а целая функция. В данном случае это закон движения механической системы q(t), определенный по крайней мере на промежутке времени между t1 и t2.
Многолетние (и это мягко сказано!) труды ученых-механиков (включая умопомрачительного Леонарда Эйлера), позволили сформулировать
Принцип наименьшего действия:
Механическая система, для которой задана функция Лагранжа
, движется таким образом, что закон её движения q(t) доставляет минимум функционалу
называемому действием по Гамильтону.
Уже из самого определения ПНД следует тот факт, что данный принцип приводит к уравнениям движения лишь для ограниченного класса механических систем. Для каких? А давайте разберемся.
Видео:Основы вариационного исчисления | уравнение Эйлера Лагранжа | 1Скачать

2. Границы применимости принципа наименьшего действия. Некоторые определения для самых маленьких
Как следует из определения, опять таки, функции Лагранжа, ПНД позволяет получить уравнения движения для механических систем, силовое воздействие на которые определяется исключительно потенциальной энергией. Для того чтобы разобраться, о каких системах идет речь, дадим несколько определений, которые, для экономии объема статьи я помещаю под спойлер
Рассмотрим движущуюся по траектории AB точку, к которой приложена сила . Бесконечно малое перемещение точки по траектории определяется вектором
, направленным по касательной к траектории.
Элементарной работой силы на перемещении
называют скалярную величину, равную
Тогда, полная работа силы на перемещении точки по траектории AB есть криволинейный интеграл
Кинетической энергией точки T называют работу, которую должны совершить приложенные к точке массой m силы, для того чтобы из состояния покоя перевести точку в движение со скоростью
В соответствии со вторым законом Ньютона
Вычислим строго стоящее под знаком интеграла скалярное произведение, для чего продифференцируем по времени скалярное произведение вектора скорости самого на себя
С другой стороны,
Дифференцируя это равенство по времени, имеем
Сравнивая (1) и (2) приходим к выводу, что
Тогда, спокойно вычисляем работу, раскрывая криволинейный интеграл через определенный, взяв в качестве пределов модуль скорости точки в начале и в конце траектории
Пусть точка перемещается в пространстве по произвольной траектории AB. Вычислим, какую работу при этом совершит сила (3)
Так как проекции силы на оси координат зависят исключительно от этих самых координат, всегда можно найти функцию
Тогда, выражение для работы преобразуется к виду
где — значения функции U(x, y, z) в точках A и B соответственно. Таким образом работа рассматриваемой нами силы не зависит от траектории точки, а определяется только значениями функции U в начале и в конце траектории. Такая сила называется консервативной силой, а соответствующая ей функция U(x, y, z) — силовой функцией. Очевидно, что
, а так же равенство нулю работы консервативной силы при движении по замкнутой траектории. Говорят так же, что функция U(x, y, z) задает в пространстве силовое поле.
Потенциальной энергией
точки, в пространстве с заданным силовым полем, называют работу внешних сил, приложенных к ней, которую они совершают при перемещении точки в заданное координатами (x, y, z) положение в пространстве из некоторого произвольного положения, выбранного в качестве начала отсчета уровня потенциальной энергии.
— потенциальная энергия точки в положении A, а
— потенциальная энергия точки в положении B. Учитывая всё вышесказанное снова вычислим работу потенциальных сил на перемещении из точки A в точку B
Таким образом, работа консервативных сил равна изменению потенциальной энергии точки, взятому с обратным знаком
причем выбор уровня, на котором мы считаем потенциальную энергию равной нулю совершенно не влияет на результат. Отсюда можно сделать вывод, что уровень отсчета потенциальной энергии можно выбрать совершенно произвольно.
Видео:9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать

3. Понятие о вариациях обобщенных координат. Постановка вариационной задачи
где s — число степеней свободы данной системы.
Действительный, но неизвестный пока нам, закон движения данной системы определяется зависимость обобщенных координат (4) от времени. Рассмотрим одну из обобщенных координат , полагая аналогичные рассуждения и для всех остальных координат.
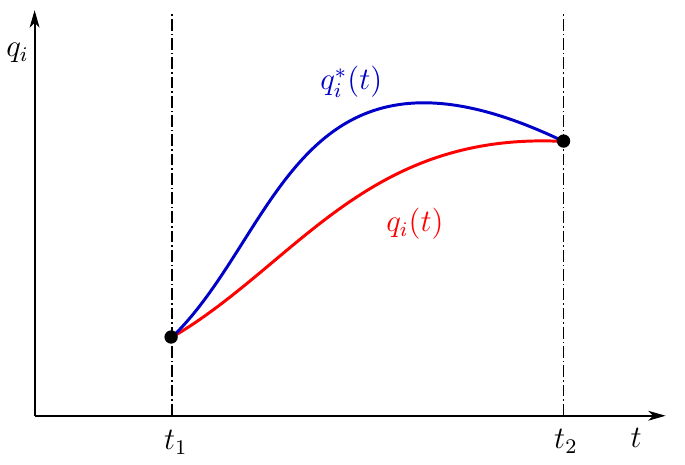
Рисунок 1. Действительное и окольное движение механической системы
На рисунке зависимость изображена красной кривой. Выберем два произвольных фиксированных момента времени t1 и t2, полагая t2 > t1. Положение системы
договоримся называть начальным положением системы, а
— конечным положением системы.
Однако, я ещё раз настаиваю на том, чтобы нижеследующий текст был прочтен внимательно! Несмотря на то, что мы задаемся начальным и конечным положением системы, ни первое положение, ни второе, нам заранее неизвестны! Равно как и неизвестен закон движения системы! Эти положения рассматриваются именно как начальное и конечное положение, безотносительно конкретных значений.
Далее мы полагаем, что из начального положения в конечное система может придти разными путями, то есть зависимость может быть любой кинематически возможной. Действительное движение системы будет существовать в единственном варианте (красная кривая), остальные кинематически возможные варианты будем называть окольными движениями
(синяя кривая на рисунке). Разность между действительным и окольным движением
будем называть изохронными вариациями обобщенных координат
В данном контексте вариации (5) следует понимать как бесконечно малые функции, выражающие отклонение окольного движения от действительного. Малая «дельта» для обозначения выбрана не случайно и подчеркивает принципиальное отличие вариации от дифференциала функции. Дифференциал — главная линейная часть приращения функции, вызванного приращением аргумента. В случае с вариацией изменение значения функции при постоянном значении аргумента вызвано изменением вида самой функции! Мы не варьируем аргумент, в роли которого выступает время, поэтому вариация называется изохронной. Мы варьируем правило по которому каждому значению времени приводится в соответствие некоторое значение обобщенных координат!
По сути, мы варьируем закон движения, по которому система из начального состояния перемещается в конечное состояние. Начальное и конечное состояние определяются действительным законом движения, но я ещё раз подчеркиваю — их конкретные значения нам не известны и могут быть любыми кинематически возможными, мы лишь полагаем, что они существуют и система гарантированно перемещается из одного положения в другое! В начальном и конечном положении системы мы не варьируем закон движения, поэтому вариации обобщенных координат в начальном и конечном положении равны нулю
Исходя из принципа наименьшего действия, действительное движение системы должно быть таким, чтобы доставлять минимум функционалу действия. Варьирование координат вызывает изменение функционала действия. Необходимым условием достижения функционалом действия экстремального значения является равенство нулю его вариации
Видео:Вывод уравнения Лагранжа 2-го родаСкачать

4. Решение вариационной задачи. Уравнения Лагранжа 2-го рода
Загоним всё под один интеграл, и так как для вариаций справедливы все операции над бесконечно малыми величинами, преобразуем этот крокодил к виду
Исходя из определения обобщенной скорости
Тогда выражение (8) преобразуется к виду
Второе слагаемое интегрируется по частям
Исходя из условия (7), имеем
тогда, получаем уравнение
При произвольных пределах интегрирования равенство нулю определенного интеграла обеспечивается равенством нулю подынтегральной функции
С учетом того, что вариации обобщенных координат независимы, (11) справедливо только в случае равенства нулю всех коэффициентов при вариациях, то есть
Никто не мешает нам умножить каждое из уравнений на (-1) и получить более привычную запись
Уравнения (12) и есть решение задачи. И вот на этом моменте ещё раз внимание — решение вариационной задачи по принципу наименьшего действия, это не функция, доставляющая минимум действию по Гамильтону, а система дифференциальных уравнений, решая которое таковую функцию можно найти. В данном случае это дифференциальное уравнение Лагранжа 2-го рода, записанное через функцию Лагранжа, то есть в формулировке для консервативных механических систем.
И всё, на этом принцип наименьшего действия заканчивается, а начинается теория обыкновенных дифференциальных уравнений, которая, в частности, гласит, что решением уравнения (12) является вектор-функция вида
где C1. C2s — произвольные константы интегрирования.
ПНД — фундаментальный принцип, позволяющий получить уравнения движения системы, для которой определена функция Лагранжа
Точка! В задачах аналитической механики вышеперечисленные выкладки больше не нужно проделывать, достаточно использовать их результат (12). Функция, удовлетворяющая уравнению (12) есть закон движения системы, удовлетворяющей ПНД.
Видео:Уравнения Лагранжа второго рода. Задача 1Скачать

5. Задача с шариком и стенкой
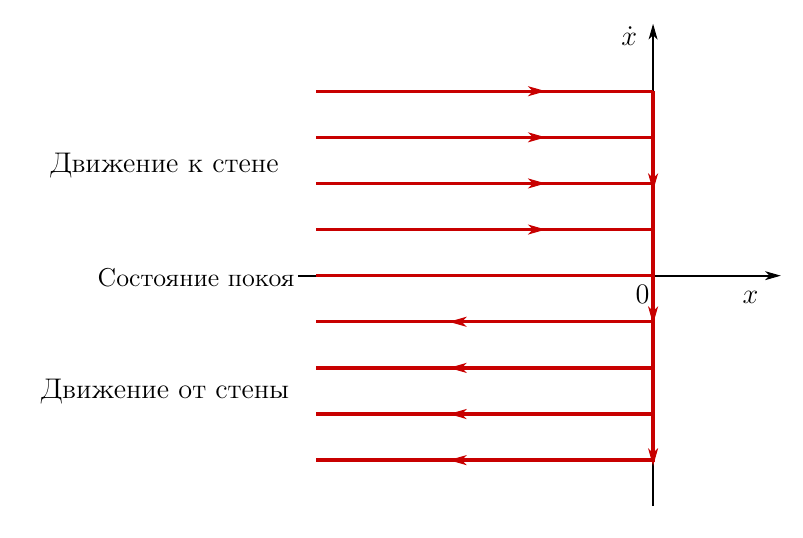
Теперь вернемся к той задаче, с которой всё началось — об одномерном движении шарика около абсолютно упругой стенки. Разумеется, для данной задачи можно получить дифференциальные уравнения движения. Так как это дифференциальные уравнения движения, то любое, я подчеркиваю это, любое их решение доставляет минимум функционалу действия, а значит ПНД выполняется! Общее решение уравнений движения шарика можно изобразить в виде так называемого фазового портрета рассматриваемой механической системы. Вот этот фазовый портрет
Рисунок 2. Фазовый портрет системы в задаче с шариком
По горизонтальной оси откладывается координата шарика, по вертикальной — проекция скорости на ось x. Может это покажется странным, но данный чертеж отражает все возможные фазовые траектории движения шарика, при любых начальных, или если вам так хочется, краевых условиях. На самом деле параллельных прямых на графике бесконечно много, на чертеже показаны некоторые из них и направление движения по фазовой траектории.
Это — общее решение уравнения движения шарика. Каждая из этих фазовых траекторий доставляет минимум функционалу действия, что непосредственно следует из выкладок, проделанных выше.
Что делает автор задачи? Он говорит: вот шарик покоится, и за промежуток времени от tA до tB действие равно нулю. Если шарик толкнуть к стенке, то за тот же промежуток времени действие будет больше, так как у шарика отличная от нуля и неизменная кинетическая энергия. Но почему шарик движется к стенке, ведь в покое действие будет меньше? Значит ПНД испытвает проблемы и не работает! Но мы обязательно решим это в следующей статье.
То что говорит автор — бред. Почему? Да потому, что он сравнивает действия на различных ветвях одной и той же действительной фазовой траектории! Между тем, при применении ПНД, сравнивается действие на действительной траектории и на множестве окольных траекторий. То есть происходит сравнение действия на реальной траектории с действием на тех траекториях, которых нет в природе, и никогда не будет!
Не понятно? Объясню ещё более доходчиво. Рассмотрим состояние покоя. Оно описывается ветвью фазового портрета, совпадающего с осью абсцисс. Координата не меняется с течением времени. Это действительное движение. А какое же движение будет окольным. Любое другое кинематически возможное. Например малые колебания шарика около рассматриваемого нами положения покоя. Задача допускает колебания шарика вдоль оси х? Допускает, значит такое движение кинематически возможно и может рассматриваться как одно их окольных
Почему же шарик таки покоится? Да потому, что действие в состоянии покоя, вычисленное на фиксированном промежутке времени от tA до tB, будет меньше действия, при малых колебаниях на том же промежутке времени. Значит колебаниям и любому другому «шевелению» шарика природа предпочитает покой. В полном соответствии с ПНД.
Допустим мы толкнули шарик в сторону стенки. Пусть мы толкнули его как хочет автор, со скоростью, подобранной из краевых условий, так чтобы в момент времени tB шарик оказался в том же положении, откуда стартовал. Шарик, с постоянной скоростью долетит до стенки, упруго отскочит и вернется в начальное положение в момент времени tB, опять таки с постоянной скоростью. Ок, это действительное движение. Какое движение будет одним из окольных? Например, если шарик будет двигаться к стенке и от стенки со скоростью, меняющейся со временем. Такое движение возможно кинематически? Возможно. Почему же модуль скорости шарика не меняется? Да потому, что действие на такой фазовой траектории будет иметь минимальное значение, в сравнении с любом другим вариантом, где скорость зависит от времени.
Вот и всё. Ничего такого волшебного тут не происходит. ПНД работает безо всяких проблем.
Видео:Уравнения Лагранжа второго родаСкачать

Выводы и пожелания
ПНД — фундаментальный закон природы. Из него, в частности, вытекают законы механики, например дифференциальные уравнения движения (12). ПНД говорит нам о том, что природа устроена так, что уравнение движения консервативной механической системы выглядит именно как выражение (12) и никак иначе. Большего от него и не требуется.
Не нужно придумывать проблем там где их нет.
Видео:Уравнение ЛагранжаСкачать

Вывод уравнения лагранжа из вариационного принципа
Философские науки, 2004, № 1, с. 105-136.
© Г.А.Голицын, А.П.Левич
Вариационные принципы в научном знании *
Г.А. Голицын, А.П. Левич
В методах научного описания мира существует крайне ограниченный набор формальных способов вводить основные законы изменчивости исследуемых систем. Почти всегда такие законы постулируются или в форме “уравнений движения” или в форме экстремального принципа. Как правило, такие формулировки равносильны: если имеется уравнение движения, то из его вида выводится функционал, для которого исходное уравнение является уравнением Эйлера-Лагранжа соответствующей вариационной задачи, и наоборот. Однако, экстремальные принципы обладают большей эвристической и обобщающей силой. Поясню сказанное простым примером. Почему камень, брошенный под углом к горизонту, движется по параболе? Можно указать на квадратичное уравнение равнопеременного движения тела. Само это уравнение представляет следствие второго закона Ньютона для тела, движущегося под действием постоянной силы. Впрочем, парабола может быть представлена и геодезической линией – решением уравнений Эйнштейна из общей теории относительности для движений в сильных полях и с высокими скоростями. Закон Ньютона и уравнения Эйнштейна могут быть выведены из принципа наименьшего действия с определенной формой экстремизируемого лагранжиана. Таким образом, существует несколько уровней объяснения явлений, каждый из которых может служить исходным постулатом. Однако, уравнения равнопеременного движения относятся лишь к узкому классу явлений, второй закон Ньютона описывает все движения в несильных полях и с невысокими скоростями, уравнения Эйнштейна лишены этих ограничений, а принцип наименьшего действия применим ко всем формам механического и электромагнитного движений.
В кратком обзоре невозможно охватить все богатство и разнообразие идей, связанных с вариационными принципами. Необходима какая-то руководящая идея для отбора материала. Такой идеей служит для нас желание получить в руки какой-то метод формулировки вариационных принципов для новых областей научного знания.
Структура научной теории
Существует ли какая-то “идеальная” форма научной теории, общая для всех научных дисциплин? Можно ли в гуманитарных и биологических науках строить теории, подобные тем, которые мы находим в физике? Если да, то почему до сих пор нет таких теорий? Некоторые биологические и гуманитарные дисциплины претендуют на звание теории, но физик отверг бы подобные притязания. Почему? Чтобы ответить на эти вопросы, нужно сначала выяснить, какие черты физических теорий дают им безоговорочное право на это наименование.
Прежде всего заметим, что любая “настоящая” (с точки зрения физика) теория имеет два этажа: помимо законов, связывающих друг с другом различные явления и образующих первый этаж теории, должен существовать второй этаж, который состоит из дедуктивных (логических) связей между самими законами. Эти логические связи позволяют выводить сами законы из других, или, следуя А. Эйнштейну, “понять эмпирическую закономерность как логическую необходимость”. Если этот второй этаж отсутствует, то данная область может рассматриваться только как совокупность эмпирических знаний, но не как теория.
Возьмем в качестве примера психологию. Психологами найдено огромное количество закономерностей и фактов, многие из них даже выражены в математической форме (Закон Вебера-Фехнера, закон Иеркса-Додсона и пр.). Но теории в строгом смысле, в каком употребляется это слово в точных науках, не существует. Причина в том, что эти законы разрознены, не образуют системы, не выводятся друг из друга или из каких-то общих принципов. Итак, жесткая дедуктивная структура, “логический скелет” есть необходимый компонент любой “настоящей” научной теории.
Но это еще не все. Как показывает история науки, логическая структура теории не остается постоянной, она эволюционирует к определенному “идеальному” состоянию. Этот идеал научной теории обрисован еще И. Ньютоном: “Объяснить как можно большее количество фактов как можно меньшим числом исходных положений”. И мы действительно наблюдаем, как в ходе эволюции теории число объясняемых фактов возрастает, а число исходных приложений (постулатов, принципов) – сокращается. В итоге оказывается, что все теории, завершившие свое развитие (такие как механика, термодинамика, геометрическая оптика и т.п.) сходны по своей логической структуре: их дедуктивные связи (образующие “второй этаж”) имеют единый центр – некоторый общий принцип.
Спрашивается, можно ли что-нибудь сказать о форме такого принципа? Является ли она для каждой области естествознания особенной или у всех теорий в этом смысле есть общие черты?
Обращаясь к теориям, которые завершили процесс централизации (механика, геометрическая оптика, термодинамика), мы находим, что в центре каждой из них стоит принцип оптимальности (иначе его называют еще экстремальным или вариационным принципом) – утверждение о минимуме (или максимуме) некоторой величины (“функционала”, “целевой функции”). В оптике это – принцип скорейшего пути Ферма, в механике – принцип наименьшего действия, в термодинамике – принцип максимума энтропии.
Случайно ли, что центральным принципом в этих (и в других) случаях оказался именно принцип оптимальности? Или у такого принципа есть определенные преимущества, которые и выводят его на центральное место в теории?
В физической и методологической литературе сложилось убеждение, что указанное обстоятельство не случайно, что экстремальный принцип обладает столь несомненными достоинствами, что у него просто нет соперников.
Из истории вариационных принципов
Мысль о том, что “природа действует простейшим образом” (И. Бернулли), т.е. “наиболее экономно”, чрезвычайно стара и послужила источником многих научных идей и методических приемов. Сошлемся еще раз на И. Ньютона, который в своих “Началах” говорил, что не должно принимать в природе иных причин сверх тех, которые истинны и достаточны для объяснения явлений, что природа ничего не дает напрасно, а было бы напрасным совершать многим то, что может быть сделано меньшим, что природа проста и не роскошествует излишними причинами вещей. Эта мысль была источником не только методологии Ньютона, но и чисто физической идеи о равенстве тяжелой и инертной масс – идеи, имевшей столь далекие последствия в общей теории относительности.
Вскоре в математике и физике идея “экономии” в природе получила воплощение в развитии экстремальных принципов. Исторически первым таким принципом был “принцип Ферма” в геометрической оптике.
Еще Герон Александрийский выводил закон отражения света из принципа кратчайшего пути. Однако уже в случае преломления света этот принцип явно нарушался; поэтому П. Ферма предположил (1662 г.), что световой луч избирает не кратчайший путь, а путь наименьшего времени. Так был сформулирован первый экстремальный принцип, оставшийся незыблемым и по сей день: “Истинный путь светового луча отличается от всех возможных (мыслимых) путей тем, что время движения вдоль него минимально”.
Вся геометрическая оптика заключена в этом принципе, как растение в зерне, и может быть получена из него путем методического развертывания с учетом конкретных условий движения света (плотность среды, наличие отражающих и преломляющих поверхностей и т.д.).
На этом примере можно видеть две основные черты, присущие всем экстремальным принципам: крайний лаконизм и простота и, в то же время, крайне общий и универсальный характер. Зная принцип Ферма, можно рассчитать любую оптическую систему, не нуждаясь ни в каких других законах геометрической оптики – все они являются лишь следствием этого принципа.
Итак, содержание всякого экстремального принципа является утверждение о минимуме (или максимуме) некоторой величины. Расчет траектории рассматривается как отыскание “истинного” пути среди всего множества возможных. Истинное движение отличается от всех возможных своей “оптимальностью”, т.е. тем, что для него некоторая величина достигает минимума (или максимума). Таким образом, основная проблема состоит в том, чтобы найти минимизируемую величину, выяснить ее конструкцию. Не всегда это так просто сделать, как в оптике: механике пришлось ждать около ста лет, прежде чем соответствующая конструкция была найдена для нее.
15-го апреля 1744 года П. Мопертюи представил Парижской Академии мемуар, в котором предлагался новый универсальный принцип механики – принцип наименьшего действия: истинное движение отличается от всех возможных тем, что для него величина действия минимальна.
Само понятие действия – как произведения массы , скорости и пути – было введено еще Г. Лейбницем, причем ему, видимо, даже было известно, что в “истинных” движениях действие имеет всегда минимальное значение. Однако Лейбниц воздержался от формулировки какого-либо общего принципа, связанного с этим свойством действия. Мопертюи же провозгласил его наиболее общим законом природы. Законы движения и покоя, по мнению Мопертюи, выведенные из этого принципа, являются точно теми, которые наблюдаются в природе, и мы можем восхищаться результатами его применения ко всем явлениям: движение животных, произрастание растений, вращение светил является только его следствиями.
Мемуар вызвал среди ученых того времени ожесточенную полемику, далеко выходящую за рамки механики. Главным предметом спора было: являются ли события, происходящие в мире, причинно обусловленными или они телеологически направляются неким высшим разумом посредством “конечных причин”, т.е. целей? Сам Мопертюи подчеркивал и отстаивал телеологический характер своего принципа и прямо утверждал, что “экономия действия” в природе доказывает существование бога.
Последний тезис вызвал резкий отпор со стороны материалистически настроенных ученых и публицистов того времени (Д´Аламбер, Дарси, Вольтер). Дискуссия велась и по другим направлениям, в частности, критиковалось определение действия, предложенное Мопертюи. Ряд авторов отрицал универсальный характер этого принципа, некоторые приводили примеры “истинных” движений, в которых “действие” не минимально, а наоборот, максимально. Велись споры и по вопросу о приоритете.
Л. Эйлер выступил в защиту приоритета Мопертюи, хотя сам сформулировал принцип наименьшего действия в более четкой и осторожной форме еще ранее него. Заслугой Мопретюи Эйлер считал универсальность его принципа; сам Эйлер рассматривал свой принцип лишь как средство решения некоторых задач механики.
Эйлер был первым, кто понял, что причинный и телеологический пути объяснения эквивалентны, хотя вначале он больше склонялся к телеологическим взглядам Мопертюи.
Окончательная формулировка принципа наименьшего действия, свободная от всякой “метафизики”, принадлежит Ж. Лагранжу.
Лагранжа больше всего интересует формальная сторона механики и мало беспокоит физическое истолкование ее уравнений. В соответствии с этим он рассматривает минимизацию действия “не как метафизический принцип, а как простой и общий вывод из законов механики”. Если Мопертюи и Эйлер рассматривали принцип наименьшего действия как первичный и основной закон механики, а все остальные законы – как его следствия, то после работ Лагранжа установилась позитивистская точка зрения, согласно которой экстремальные принципы суть только изящная и компактная упаковка для большого количества опытных фактов, не вносящая ничего нового в уже известные законы. Всякая попытка вернуть экстремальным принципам их прежнее положение – фундамента науки – клеймилась как теологическая. И только в ХХ веке революция, вызванная в физике теорией относительности и квантовой механикой, привела к пересмотру роли и места экстремальных принципов.
Выяснилось, что понятия и законы, лежащие в основании ньютоновской физики, не являются абсолютными: они изменяются при переходе от одной системы отсчета к другой. Действительно, основными законами природы могут считаться лишь те, которые остаются неизменными в любой системе отсчета. Оказалось, что этому требованию отвечают лишь экстремальные принципы. Можно считать, что в настоящее время этот спор решен окончательно: основные законы физики (а весьма вероятно, что и любой другой науки) должны иметь экстремальную форму [20].
Если стихийное развитие научной теории направлено к определенному идеалу, то ученый, очевидно, сэкономит себе силы и время, если уяснит себе форму этого идеала и будет стремиться к нему сознательно. Особенно успешным может оказаться такой подход в областях знания, которые еще не обрели строгой теоретической формы.
История действительно знает попытки такого рода. Открытие экстремальных принципов в свое время породило надежду, что к законам природы можно идти не только “снизу”, путем индукции, обобщения фактов, но и “сверху”, путем дедукции от экстремальных принципов. Эйлер, в частности, считал, что для этого только нужно путем общих “метафизических” рассуждений найти величину, которую “экономит” природа в данной области естествознания (т.е. “целевую функцию”, “функционал”), и сформулировать соответствующий экстремальный принцип. В скрытом виде он содержит все нужные нам законы; получить их в явной форме – дело простой математической ловкости.
Несмотря на соблазнительную простоту этой программы, реализовать ее в то время ни разу не удалось – ни самому Эйлеру, ни тем, кто пытался следовать за ним. Причина этого достаточно очевидна: не существовало никакого регулярного метода для отыскания экстремизируемой величины. Механике и оптике в этом смысле повезло: соответствующие величины были для них достаточно простыми и, в сущности, могли быть найдены путем перебора. Но уже в термодинамике максимизируемая величина – энтропия – не обладает ни простотой, ни достаточно очевидным физическим смыслом.
После ряда неудач программа Эйлера по отысканию законов природы “сверху” была заброшена. Более того, сами вариационные принципы были взяты под подозрение и урезаны в своих правах вследствие своего рода “телефобии”, которой была заражена позитивистски настроенная наука XIX века.
Спрашивается, не появились ли в наше время какие-нибудь новые предпосылки, позволяющие надеяться на успех реализации программы Эйлера?
На наш взгляд – появились. Прежде всего умножилось само число вариационных принципов, возникла возможность сравнивать, комбинировать и обобщать.
Далее, сложилось боле глубокое понимание некоторых идей, связанных с вариационными принципами: (“сила”, “связь”, “равновесие” и пр.). Стало, в частности, ясно, что специфические, сложные и разнообразные интегральные вариационные принципы механики могут быть получены как следствие более простых и общих дифференциальных принципов. А эти последние могут быть представлены в единообразной форме, выражающей идею равновесия системы [9]:
Здесь – вектор обобщенной силы; – вектор возможных движений системы, совместимых с наложенными на нее связями.
Условие (1) означает ортогональность этих двух векторов: проекция силы на поверхность возможных движений системы равна нулю. Этим действительное (равновесное) состояние системы выделяется среди множества возможных. Иллюстрацией может служить известный в механике принцип возможных перемещений. Принцип позволяет найти равновесное состояние системы, которое – в случае его устойчивости – и совпадет с истинным состоянием.
В термодинамике условия равновесия, как их сформулировал Гиббс, являются другим примером вариационного принципа (1).
Очень часто силы могут быть получены как частные производные от некоторого потенциала по соответствующим координатам:
Тогда произведения могут рассматриваться как вариации этого потенциала, а сам принцип может быть записан в более компактной скалярной форме
Т.е. равновесное, истинное состояние системы определяется как точка стационарности потенциала.
В 1743 г. Д´Аламбер сформулировал принцип, позволивший распространить идею равновесия на динамику. К активным силам он добавил силы инерции . В этом случае истинное состояние (движение) системы выделяется из всего множества возможных тем, что для него вектор суммарной силы ортогонален любому вектору возможных перемещений :
Стоит подробнее остановиться на принципе Д´Аламбра, чтобы оценить ту важную идею, которую он вносит и которая может иметь далеко идущие последствия. Идея состоит в том, что понятие равновесия относительно. Нельзя говорить о равновесии, предварительно не указав тех факторов – сил и связей, которые уравновешиваются.
Система, неравновесная относительно одного набора факторов, может оказаться равновесной относительно другого.
Так атомное ядро неравновесно относительно кулоновских сил (протоны отталкиваются). Но может быть сделано равновесным за счет добавления ядерных сил. Живой организм неравновесен относительно термодинамических сил, но может быть сделан равновесным за счет добавления специальных управляющих сил.
Дело еще и в том, как определяется равновесие, что служит критерием равновесности или неравновесности. Чаще всего под равновесием по данной переменной понимают такое состояние, (значение ) в котором обращается в нуль скорость изменения . Но иногда под равновесием понимают обращение в нуль суммы сил, действующих на данную переменную. Последнее понимание является более общим. Оно включает в себя не только статистическое равновесие (когда скорость изменения переменной равна нулю), но и различные формы динамических равновесных (“стационарных”) состояний. В таких состояниях ряд переменных может изменяться с постоянной скоростью . И даже падение с постоянным ускорение в поле тяжести может – в духе теории тяготения Эйнштейна – рассматриваться как движение в отсутствие сил, т.е. как равновесное.
В 1829 году Гаусс предложил еще один общий принцип механики, который он назвал принципом наименьшего принуждения:
Здесь – вектор возможных ускорений.
Наконец, в 1903 году Журден обнаружил существование третьего вариационного принципа механики:
где в качестве варьируемой переменной выступает скорость .
Сравнение трех принципов (2), (3), (4) показывает, что довольно безразлично, с помощью какой переменной – , или задается поверхность возможных движений, совместимых со связями, наложенными на систему. Тем не менее следует отметить, что принципы Журдена и Гаусса являются более общими, поскольку позволяют учитывать не только голономные (“позиционные”), ни и неголономные (“скоростные”) связи. Однако вычислительные трудности, связанные с использованием этих принципов, привели к тому, что они не стали столь популярными, как принцип Д´Аламбера.
Привлекательность принципа Гаусса еще и в том, что в роли “потенциала” для него выступает простая квадратичная форма
которую Гаусс назвал принуждением. Сам принцип может быть записан в виде требования минимума этой квадратичной формы: .
Дьярмарти (1974) в поисках наиболее общей формы для вариационных принципов линейной неравновесной термодинамики пришел к принципу, который он также назвал принципом наименьшего принуждения – по аналогии с принципом Гаусса:
где – обобщенные термодинамические силы, – потоки, – сопротивления.
В этом случае, однако, возможна и более общая форма принципа, включающая помимо “диагональных” членов ( ) также и смешанные члены ( ):
Такого рода квадратичные формы являются весьма типичными, поскольку любой потенциал вблизи точки экстремума может быть аппроксимирован такой формой. Это соответствует линейной аппроксимации зависимости между силами и координатами: . Можно надеяться, что именно такая форма принципа – хотя бы как аппроксимация – является универсальной, справедлива не только для механики или термодинамики, но и для других дисциплин.
Наиболее общая формулировка принципа наименьшего принуждения, не зависящая от природы системы, может быть получена так.
Пусть – равновесное, нормальное состояние системы; это состояние, в которое система переходит под действием внутренних сил (“реакций”) когда внешние силы отсутствуют.
Будем предполагать, что реакция пропорциональна отклонению переменной от равновесия (нормы) и обратна по знаку этому отклонению , т.е. мы предполагаем, что система линейна и статически устойчива.
Пусть – внешняя сила, действующая на переменную (“приведенная” к этой переменной); в частном случае эта сила может быть и равной нулю.
Пусть, наконец, – действительное значение переменной, действительное состояние системы.
Тогда действительное состояние отличается от всего множества возможных тем, что принуждение для него минимально:
Отсюда следует также дифференциальная форма принципа:
(значения , , фиксированы и варьирует только ).
В отсутствие внешних сил ( ) принцип (5) принимает вид:
Действительное состояние определяется только связями между переменными .
Наконец, если и связи отсутствуют (переменные независимы), то действительное состояние совпадает с нормой , которая и является истинным, “наиболее равновесным” состоянием системы. Принуждение при этом обращается в нуль.
Итак, приступая к формулировке вариационного принципа для какой-нибудь новой области естествознания мы можем считать, что форма минимизируемой величины нам – в первом приближении – известна. Это квадратичная форма (5). Для ее полного определения нужно найти весовые коэффициенты . Как это можно было бы сделать? Здесь просматриваются два пути:
1) Прежде всего можно определить экспериментально. Если мы умеем измерять обобщенные силы и отклонения переменных от нормы , то весовой коэффициент определяется как отношение
Проблема в том, что чаще всего мы это делать не умеем. Механика и термодинамика являются счастливым исключением, но в других дисциплинах, как правило, методы измерения нужно создавать заново. При этом, помимо технических трудностей, возникают и непростые теоретические и методологические проблемы. В основном они связаны с понятием обобщенной силы, ее опрерациональным определением.
В механике и термодинамике обобщенные силы определяются через понятие энергии, как частные производные от некоторого потенциала по координатам. Но как определять обобщенные силы за пределами физики? Что делать, если нет понятия энергии или оно не играет определяющей роли в поведении системы? Выше мы определяли обобщенную силу (обобщенный) потенциал как частную производную от этого потенциала по соответствующей координате, т.е. как понятие вторичное. Но что делать, когда именно потенциал не известен и его нужно определить через силу, когда сила является первичным, исходным понятием?
Короче говоря, нужно независимое операциональное определение обобщенной силы.
2) Второй, более плодотворный, но и более трудный путь состоит в том, чтобы обратиться к “метафизическим” соображениям и попытаться понять, какая “истинная” минимизируемая величина скрывается за квадратичной аппроксимацией. При этом квадратичная форма служит всего лишь наводящим мостиком и особенно важно исследовать границы ее применимости, т.е. случаи, когда она перестает работать.
Широкое обобщение понятия силы и соответствующего понятия координаты, возможность преобразования этих величин приводят к важному наблюдению, что во многих ситуациях они являются относительными или, как обычно говорят, “двойственными”: сила может выступать в роли координаты, а координата – в роли силы. Глубокие основания этой двойственности лежат в относительности самих понятий причины и следствия: причина сама обычно является следствием какой-то другой причины, а следствие может стать причиной других следствий. Уже в механике мы видим, что активная сила является причиной изменения состояния (например, ускорения) системы, а изменение состояния в свою очередь служит причиной появления реакции системы (например, силы инерции). Еще более сложную взаимосвязь причин и следствий мы находим в процессах управления. Двойственность служит формальным выражением этой относительности.
Проблема двойственности наиболее полную разработку получила в теории оптимального управления (методы оптимизации, линейное и нелинейное программирование, математическая экономика [5]). Выглядит она следующим образом: пусть требуется найти максимум целевой функции
где – вектор, при наличии ограничений
Для решения задачи обычно используют метод множителей Лагранжа: строят функцию Лагранжа
и ищут ее максимум уже безо всяких ограничений. Переменные – множители Лагранжа. Эта задача называется прямой.
Однако множители Лагранжа изначально являются неопределенными. Поэтому возникает вторая задача – найти значения множителей Лагранжа, обеспечивающие максимум . Это и есть двойственная задача. В общем случае двойственные переменные – множители Лагранжа – также могут быть подвержены ограничениям. Такие ограничения должны быть согласованы с ограничениями на переменные .
Наиболее просто связь между условиями прямой и двойственной задачи выглядит в линейном программировании. Прямая задача: максимизировать целевую функцию при условиях . Двойственная задача: минимизировать целевую функцию при условиях . Здесь – векторы, – матрица. Одна из наиболее наглядных интерпретаций этих величин имеет место в экономике: – производимый продукт, – продажная цена единицы продукта, – получаемый доход, – ресурс, необходимый для производства продуктов, – стоимость единицы ресурса, – затраты на производство. Элементы матрицы – затраты -го ресурса на производство -го продукта (эта интерпретация с некоторой корректировкой терминов применима и в биологии).
Добавим, что ограничения в экономике обычно задаются в виде неравенств. Однако решение, как правило, лежит на границе допустимой области и в этом случае можно обойтись равенствами.
Доказан целый ряд теорем, касающихся свойств прямой и двойственной задачи и связей между ними. В частности показано, что если решение вообще существует, то оно совпадает в обеих задачах.
Существование двойственности обнаружено также в ряде областей физики, связанных с экстремальными принципами (механика, термодинамика и пр.). Массье (1869) первый обратил внимание на то, что в качестве независимых переменных, определяющих состояние системы, можно одинаково выбирать и энергию, и энтропию ([8], с.219). Позднее Гиббс (1875) развил метод термодинамических потенциалов – “равноправных” функций состояния системы, которые одинаково хорошо можно использовать для описания и вывода уравнений системы, выбирая наиболее удобную функцию в зависимости от характера наложенных на систему ограничений (иначе говоря – независимых, извне задаваемых переменных). Например, вариационный принцип, устанавливающий критерий равновесия изолированной системы Гиббс формулирует следующим образом:
1) “Для равновесия любой изолированной системы необходимо и достаточно, чтобы при всех возможных изменениях состояния системы, не влияющих на ее энергию, вариация энтропии исчезала или была отрицательной”: при .
2) “Для равновесия любой изолированной системы необходимо и достаточно, чтобы при всех возможных изменениях состояния системы, не влияющих на ее энтропию, вариация ее энергии исчезала или была положительной”: при (цит. по [22], с. 208).
В экологии сообществ предложено [16] обобщение теоремы Гиббса. Рассматривается вариационная задача на условный экстремум [13, 15]
где – искомые численности каждого из видов сообщества в стационарном состоянии, – количество -го ресурса, потребленное популяцией вида из среды в расчете на одну клетку к моменту остановки роста; – общее количество взаимонезаменимых ресурсов, потребляемых сообществом; – число видов в сообществе; – начальное содержание ресурса в среде .
Задача (6) является математической формализацией постулируемого экстремального принципа, согласно которому динамическая система из заданного состояния переходит в состояние с экстремальной (в пределах, допустимых имеющимися ресурсами) структурой [13, 37].
Приведем некоторые возможные интерпретации функционала и сформулированного экстремального принципа.
Энтропия может рассматриваться как мера “структурированности” некоторого состояния или мера “удаленности” структуры состояния от его бесструктурного аналога [14].
Энтропия, линейно упорядочивая сами структуры и описываемые математическими структурами состояния естественных систем, в определенном смысле в рамках функторного метода сравнения математических структур [13] обобщает понятие “количество элементов” для конечных структурированных множеств [14]. Тем самым, экстремальный принцип реализует максимум экспансии сообществ живых организмов [37].
Энтропию системы можно рассматривать как количество информации, связанной со структурой системы, поэтому введенный экстремальный принцип можно интерпретировать и в информационных терминах [13].
Согласно обсуждаемой “теореме Гиббса” энтропийный экстремальный принцип с ограничениями по ресурсам равносилен принципу минимального потребления любого из лимитирующих динамику ресурсных факторов с ограничениями на наименьшую допустимую величину энтропийной характеристики системы.
порождающего динамику сообщества, можно интерпретировать и как требование максимального разнообразия системы, ограниченного доступными ресурсами среды [12].
При исследовании сформулированной экстремальной задачи (6) при условии был получен ряд строгих результатов, среди которых следующие [15]:
Максимум в задаче (6) достигается в точке, где
Теорема существования и единственности: для любого вектора ресурсов решение задачи (6) существует, единственно и задается формулой видовой структуры
где а общая численность и вектор есть решения системы алгебраических уравнений
Теорема стратификации: все пространство ресурсов
является объединением непересекающихся подмножеств (стратов), находящихся во взаимно-однозначном соответствии с непустыми подмножествами множества в том смысле, что если некоторый вектор принадлежит подмножеству пространства ресурсов, соответствующему , то для этого вектора задача (6) эквивалентна задаче с равенствами
Заметим, что задача с неравенствами (6) сводится (редуцируется) к задачам с равенствами и в каждом страте решение задачи (7) зависит только от ресурсов (и потребностей в них), принадлежащих подмножеству . Причем именно эти ресурсы (и только они) потребляются полностью (являются лимитирующими), т.е. соответствующие неравенства из ограничений обращаются в равенства.
“Теорема Гиббса”. Пусть мы имеем вектор соответствующий решению (7) задачи (6), и пусть Пусть данный вектор ресурсов принадлежит некоторому страту , причем для , для . Рассмотрим следующую экстремальную задачу:
Тогда решение (7) задачи (6) является одновременно решением системы (8). Верно и обратное утверждение: если вектор – решение системы (8), то вектор будет и решением задачи (6) с
В статистике переменными являются вероятности. В качестве “действительного состояния” системы, отвечающего некоторому критерию оптимальности и выделяющемуся среди множества возможных, рассматривается распределение вероятностей. Обычно ¬ это в каком-то смысле “равновесное” распределение. Однако равновесие, как правило, надо понимать обобщенно (см. принцип Д´Аламбера (2)). Таково, например, “стационарное состояние”.
Первостепенным является вопрос о статических (вероятностных) силах, определяющих это равновесие.
Из требования аддитивности силы следует, что сила должна быть связна не с самой вероятностью события, а с ее логарифмом. В самом деле, известно, что вероятности независимых событий перемножаются, и только логарифмы их складываются:
И если мы определим силу как
Как же выглядит условие равновесия в вероятностном случае?
Пусть по оси действует сила , которая в этом случае может быть задана через потенциал Эта сила вызывает отклонение распределения вероятностей от исходного равновесного состояния и порождает соответствующую реакцию системы Последняя пропорциональна разности “вероятностных” сил, возникающих в соседних точках оси:
В новом равновесном состоянии сумма активной силы и реакции системы равна нулю:
где – нормировочный множитель.
Мы получили известное распределение Больцмана, исходя из общих предпосылок (аддитивность силы) и для самого общего случая, независимо от природы системы и действующих в них сил.
Квадратичная форма (5) (принцип наименьшего принуждения) также справедлива в статистике как первое приближение.
В роли переменных опять выступают вероятности
Пусть — равновесное значение вероятности; — действительное значение; — внешняя сила.
Что касается жесткости равновесного состояния , то, как следует из (9), за нее следует принять величину, обратную вероятности состояния .
Тогда принцип наименьшего принуждения может быть записан в виде:
Если внешние силы равны нулю, то мы получаем принцип свободного поведения:
Здесь левая часть — известное выражение для критерия согласия Пирсона. При отсутствии внешних сил действительное распределение вероятностей (состояние системы) находится в наилучшем согласии с равновесным (нормальным) состоянием , какое только допускают связи, наложенные на вероятности . Если связи отсутствуют, то действительное состояние совпадает с равновесным и принуждение обращается в нуль.
Известно, однако, что квадратичная форма (10) является всего лишь аппроксимацией более фундаментальной величины, а именно, так называемой “дивергенцией” Кульбака [11]:
Эта величина, как и величина всегда отрицательна и обращается в нуль только при . Используя для логарифма аппроксимацию можем переписать (11) в виде:
что совпадает с (7).
Все выше сказанное наводит на мысль, что истинными величинами, входящими в статистические экстремальные принципы должны быть логарифмические формы — информация, энтропия и связанные с ними понятия. Из таких принципов мы рассмотрим два, которые стали важными вехами на пути развития этого направления:
1. Так называемый, “формализм Джейнса”, возникший как обобщение известного физического принципа максимума энтропии, но получивший широкое распространение и за пределами физики [34].
2. Принцип “минимума различающей информации” Кульбака, возникший в недрах статистики как обобщение и теоретическое обоснование множества известных эмпирических методов и приобретающий ныне все более общее значение и за пределами статистики [11].
В работах Джейнса [34] был предложен метод отыскания равновесных распределений вероятности при наличии дополнительных условий. В основе его лежит широкое обобщение принципа максимума энтропии и сочетание его с методом множителей Лагранжа.
Идея формализма является развитием известного “принципа недостаточного основания”: если нам ничего не известно о величине , кроме того, что она лежит в некотором ограниченном диапазоне, то разумнее всего принять, что вероятности распределены в этом диапазоне равномерно. Потому что у нас нет доказательств, чтобы считать одно значение более вероятным, чем другое.
Но этот результат может быть получен также из принципа максимума энтропии, которая может рассматриваться как мера нашего незнания — и это самый честный и непредвзятый подход к определению вероятностей .
Однако этот подход может быть обобщен и на те случаи, когда нам что-то известно о величине , например, среднее значение некоторой функции от :
Для отыскания “самого непредвзятого” распределения в этом случае мы можем снова использовать требование максимизации энтропии
но на этот раз с учетом имеющейся у нас информации о среднем значении функции .
Для учета дополнительных условий (их может быть несколько) используется метод множителей Лагранжа.
С учетом условия нормировки, наложенной на вероятности
и дополнительных условий мы можем построить функцию Лагранжа:
Оптимальное (равновесное) распределение, отвечающее максимуму этой функции, имеет вид:
Множитель может быть найден из условия нормировки:
и выражение для может быть переписано:
Это обобщение распределения Больцмана на случай, когда имеется несколько ограничений (несколько “потенциалов” ).
Если в число координат входят и скорости, то мы получаем и распределение Гиббса (в этом случае — “кинетический потенциал”). Вообще все основные результаты равновесной термодинамики могут быть получены на основе этого подхода.
Следует отметить, что простой, изящный и универсальный формализм Джейнса до сих пор еще редко находит место в учебниках физики, хотя способен намного облегчить жизнь и студентам и преподавателям. До сих пор для вывода статических распределений и вытекающих из них термодинамических функций используются громоздкие методы, восходящие еще к Гиббсу, сложные модели, не имеющие универсального значения. Чем это объяснить?
Одна из версий состоит в том, что принцип максимума энтропии в трактовке Джейнса (как меры незнания) имеет характер скорее логический, чем физический, говорит о субъективных свойствах нашего познания, а не об объективных законах природы. В определенном смысле он чужероден для физики – хотя, казалось бы, квантовая механика должны была приучить нас к мысли, что субъект и объект познания связаны теснее, чем казалось когда-то.
Как бы то ни было, но принцип максимума энтропии в трактовке Джейнса, постепенно завоевывает физику. (См., например, [26], [29]).
Однако наиболее успешное применение он нашел за пределами физики: в лингвистике [19], математике [32, 39], экономике [2, 17, 23], биологии [25], психологии [4], теории распознавания образов [6, 33], инженерной деятельности [10].
Интересно, что в последние годы к принципу все чаще обращаются социологи, экономисты, лингвисты, инженеры и т.п. Представьте себе, что вам нужно оценить количество электродвигателей разной мощности на каком-нибудь крупном предприятии [10]. Если известна суммарная мощность, потребляемая предприятием, то вам незачем ходить по цехам и пересчитывать двигатели — равновесное распределение двигателей по мощностям вы можете с достаточной точностью получить из принципа максимума энтропии с учетом ограничения на мощность. Разумеется, двигатели не сами так распределились — их распределили люди, бессознательно руководствуясь эти принципом.
Формализм Джейнса позволяет достаточно просто подойти и к отысканию равновесных состояний биологических сообществ при различных дополнительных условиях. Проблема эта имеет важные практические приложения, в частности в экологии и постоянно привлекает внимание исследователей (см., например, работы А.К. Прица [21], Ю.М. Свирежева и Д.О. Логофета [24], Д. Лурье и Х.Вагесберга [18], А.П. Левича [12, 37], а также раздел по проблеме двойственности настоящего обзора).
Однако, основная проблема в применении этого принципа состоит в отсутствии явных процедур для сопоставления каждой из исследуемых систем адекватного ее природе энтропийного функционала. Даже в прародительнице энтропии — статистической физике — подходы к расчету энтропии в интересующих исследователя случаях крайне ограничены (как сетовал И. Пригожин, формулировка второго начала с точки зрения современного физика представляет собой скорее программу, чем утверждение, допускающее однозначную интерпретацию, так как ни Томпсон, ни Клаузис не указали точный рецепт, позволяющий выразить изменение энтропии через наблюдаемые величины). Поэтому обычная практика при работе с принципом максимума энтропии состоит в постулировании для исследуемой системы какого-либо аналога формул Больцмана или Шеннона. Наиболее последовательно указанная тенденция проявляет себя как раз в формализме Джейнса. Метод исследования систем Эдвина Томсона Джейнса состоит из нескольких рекомендаций:
Сопоставить допустимым состоянием системы определенные значения вероятности их реализации.
Сформулировать в виде неравенств ограничения на макропараметры системы (например, законы сохранения энергии, числа частиц и т.д.).
Отыскать равновесное состояние системы методом множителей Лагранжа как решения задачи на условный максимум с функционалом в форме шенновской энтропии.
Появившись в конце 60-х годов прошедшего века в статистической физике, формализм Джейнса прошествовал по многим областям знания, добавив к проблеме обоснования энтропийного функционала и проблему адекватного выбора ограничений на его экстремум, поскольку до решения вариационной задачи не известно, для каких макропараметров должны выполняться ограничения в виде строгих равенств.
Обратимся теперь к другому общему принципу статистики, имеющему экстремальную форму — принципа минимума различающей информации.
Понятие “различающей информации”
введенное и исследованное в работах Реньи [38] и Кульбака [11], тесно связано с упоминавшимся выше понятием дивергенции Кульбака:
В самом деле, как следует их этих формул:
Обе величины обладают сходными свойствами: неотрицательны; обращаются в нуль только, когда оба распределения совпадают Их различие в том, что дивергенция симметрична относительно обоих распределений; различающая информация такой полной симметрии не имеет, но зато проще. Обе величины с одинаковым успехом могут использоваться в качестве критерия согласия (или различия) двух распределений, причем критерия очень общего. Легко показать, что известные критерии Фишера, Стьюдента, Пирсона и пр. являются частными случаями этого критерия.
Однако с точки зрения наших целей наиболее интересны для нас результаты, связанные с использованием критерия “минимума различающей информации” для разыскания равновесных распределений вероятностей. Причем, это равновесие более общего типа, чем те, которые получаются на основе формализма Джейнса. Последний является частным случаем подхода, основанного на требовании минимума различающей информации:
В самом деле, можно видеть, что если и не зависит от , то это выражение сводится к требованию максимума энтропии.
Однако в более общем случае распределение неравномерно. Если оно нам не задано и не может меняться, то возникает задача: отыскать распределение , наиболее близкое к заданному. Мерой близости служит различающая информация.
Если на не наложено никаких ограничений, то решение задачи тривиально: совпадает с . Наиболее интересны случаи, когда на наложены дополнительные условия типа тех, которые мы встречали в методе Джейнса. Например, заданы средние значения некоторых функций от :
Идеология применения формализма Кульбака может быть переосмыслена так: пусть нам известно некоторое “априорное” (здесь его называют “образующим”) распределение и какая-то дополнительная информация о величине , например, среднее значение некоторой функции . Тогда наилучшим, “самым непредвзятым” апостериорным распределением будет то, которое минимально отличается от априорного — с учетом дополнительного условия для функции . Вообще говоря, таких условий может быть несколько.
Тогда мы можем обычным образом составить функцию Лагранжа
и найти значения , доставляющие ей минимум. Решение имеет вид:
В отличие от (12) здесь в правую часть входит в виде множителя априорное распределение Если , то мы, как и следовало ожидать, получаем выражение (12).
Возможен и еще один подход: как правило, априорное распределение может быть представлено в экспоненциальной форме
где — некий фиктивный “потенциал”, отражающий имеющуюся у нас априорную информацию об . Тогда выражение для приобретает однородную форму:
Это распределение может быть получено и на основе формализма Джейнса, если к числу дополнительных условий добавить Таким образом оба формализма приводят к одинаковым результатам; и оба позволяют учесть имеющуюся у нас априорную информацию — либо в виде априорного распределение , либо в форме фиктивного дополнительного условия
На этом примере хорошо видна также относительность понятия равновесия: мы можем либо считать равновесным равномерное распределение вероятностей, а неравномерное рассматривать как отклонение от равновесия под действием потенциальной внешней силы , введенного как дополнительное условие. Либо упрятать это условие внутрь системы, а возникающее при этом неравномерное распределение рассматривать как равновесное.
Принцип минимума различающей информации может рассматриваться как наиболее общий статистический аналог принципа наименьшего принуждения Гаусса (5). В качестве источников активных внешних сил здесь выступают потенциалы ; а пассивные силы (реакции) порождаются отклонением вероятностей от заданных, нормальных значений .
Легко показать, что в частном случае, когда — гауссово распределение, из принципа минимума различающей информации следует знаменитый метод наименьших квадратов Гаусса. Как известно, сам Гаусс усматривал в нем глубокую аналогию с принципом наименьшего принуждения.
Кульбак показал [11], что и многие другие известные результаты статистики могут быть получены как следствие принципа (13). Таковы метод максимума правдоподобия, методы классификации, регрессионного, корреляционного и факторного анализа, анализа таблиц сопряженности и пр.
Интересны и те приложения, которые получило понятие различающей информации за пределами собственно статистики.
Оприраясь на понятие различающей информации Шлегль [30] смог дать статистическое обоснование критерию устойчивости Гленсдорфа-Пригожина [3]. Шлегль показал, что эта величина связана со второй вариацией энтропии, которую применяли для той же цели сами Гленсдорф и Пригожин. Различающая информация — положительно определенная функция вероятностей, так что ее можно использовать в качестве функции Ляпунова для проверки устойчивости. Тогда получаем так называемый критерий устойчивости Шлегеля — статистический аналог критерия Гленсдорфа-Пригожина где — производство энтропии. (Индекс означает, что рассматривается только та часть изменения , которая обусловлена изменением сил ).
Обратим внимание на то, что в отличие от энтропии, различающая информация не является функцией состояния системы (т.е. значений ): она зависит также от “заданного”, “нормального” распределения вероятностей . Это сближает ее также с локальными потенциалами , введенными Гленсдорфом и Пригожиным.
Об экстремальных принципах биологии
Экстремальные принципы биологии находятся в стадии становления. Поэтому естественны и большое разнообразие этих принципов и не очень четкая порой их формулировка. Дело осложняется и тем, что живая материя организована в сложные иерархически системы: биосфера — биоценозы — популяции — особи — органы и ткани — клетки — органеллы — молекулы. И на каждом уровне организации могут существовать свои критерии оптимальности. Приложение принципа максимума энтропии к экологическим сообществам продемонстрировано в предыдущих разделах. Подробный обзор приложения экстремальных принципов в математической биологии опубликован недавно в работах с участием одного из авторов [27, 28]. В данном разделе обратим внимание на то, что для биологических систем чрезвычайно типичны и важны такие процессы как потеря устойчивости, уход от равновесия и переход к новому равновесию. Такие процессы мы наблюдаем на всех уровнях организации — от клеток и молекул до биоценозов и биосферы в целом. Развитие индивида, поведение, творчество, эволюция биосферы — основаны именно на таких неустойчивых процессах. Желательно было бы найти экстремальный принцип, который с одной стороны адекватно описывал бы динамику этих процессов, а с другой — сохранял бы преемственность по отношению к известным экстремальным принципам, включая их в себя как предельные частные случаи.
Одна из наиболее интересных попыток такого рода принадлежит Эйгену [31]. Составленное им эволюционное уравнение описывает эволюцию некоего сообщества видов. (Последние могут трактоваться очень широко, так что уравнение пригодно, например, для описания процессов восприятия). Вообще говоря, подобное уравнение — или его общий аналог — может быть получено как следствие некоторого экстремального принципа. Что это может быть за принцип?
Нам кажется, что в поисках такого принципа нужно исходить из центральной аксиомы биологии: живой организм формируется в процессе адаптации к условиям окружающей среды. Адаптированность, приспособленность является условием выживания в этой среде и определяет все реакции и свойства организма. Формальное описание этого факта могло бы послужить отправной точкой поиска.
В ряде работ (см., например, [4]) было выдвинуто предположение, что наиболее общей и адекватной мерой адаптации системы к окружению является средняя взаимная информация между условиями среды и признаками или реакциями системы . А основным принципом, определяющим поведение и развитие системы, является принцип максимума информации:
Здесь — условная и безусловная энтропия, — условная и безусловная вероятность.
В своих работах по теории информации А.Н. Колмагоров показал [7], что под величинами не обязательно понимать вероятности, это могут быть просто относительные доли, части, концентрации. Подход Колмагорова, сохраняя основной математический аппарат теории информации, в то же время резко расширяет сферу применимости.
Принцип максимума информации означает, что по мере адаптации к среде признаки и реакции организма со все большей полнотой и точностью отражают условия среды. У хорошо приспособленного организма эта взаимная информация так велика, что биолог, наблюдая признаки организма, может довольно точно описать условия среды, в которой он обитает. И наоборот, зная условия среды, можно довольно правильно предсказать признаки организма, способного выжить в этой среде.
Заметим, что принцип максимума информации включает в себя и принцип максимума энтропии при фиксированном .
Из этого принципа следует также эволюционное уравнение, сходное с уравнением Эйгена, но в некоторых отношениях более общее:
Здесь — информативность признака в условиях ; — средняя информативность; — относительная доля /“вероятность”/ комбинации .
Из приведенного уравнения видно, что в отличие от уравнения Эйгена, информативность, характеризующая селективное преимущество признака, зависит от условий среды . Поэтому не только изменение признака /мутация/, но и изменение условий среды может изменить информативность и дать толчок новому направлению эволюции. Система эволюционирует вместе с окружающей средой — это, конечно, более реалистическая точка зрения; и примеров, когда равновесие нарушалось именно изменением условий среды, давая преимущество одним видам и уничтожая другие, — можно найти огромное количество.
Система уравнений (14) задает некоторое преобразование начального состояния /вектора вероятностей/ системы в конечное, равновесное. Число таких возможных равновесных состояний определяется числом собственных векторов линеаризованного преобразования. Неустойчивость процесса проявляется в том, что ничтожное изменение начальных условий может совершенно изменить ход эволюции и привести систему к другому “аттрактору” /равновесному состоянию/. Таким образом, принцип максимума информации и эволюционное уравнение (14) описывают не только устойчивый процесс выбора вблизи равновесного состояния, в точке бифуркации эволюционного процесса. Таким образом, принцип максимума взаимной информации является более общим, чем принцип минимума различающей информации и переходит в последний только вблизи равновесия. Покажем это более подробно.
Пусть система достигла одного из равновесных состояний, характеризуемых распределением вероятностей . Взаимная информация между и в этом состоянии может быть разбита на две части следующим образом:
Здесь — состояние, близкое к равновесному /возникшее, например, вследствие како-то флуктуации/; — различающая способность между и ; — взаимная информация, усредненная по . Поскольку вблизи равновесия , то приближенно можем заменить эту величину на среднюю взаимную информацию между и , т.е. на . Поскольку постоянна и не варьируется, то и выражение в целом постоянно. Поэтому требование максимизации взаимной информации равносильно требованию минимума различающей информации , т.е. вблизи равновесного состояния принцип максимума взаимной информации переходит в принцип минимума различающей информации. Но – только вблизи равновесия. Вообще же принцип максимума информации является более общим и адекватно описывает также процессы вдали от равновесия.
Более подробное обсуждение и некоторые дополнительные аргументы в пользу принципа максимума взаимной информации можно найти в работе [4].
В заключение можно сказать, что обобщенный принцип равновесия в форме (1), принцип наименьшего принуждение (5) и его статистический аналог – принцип максимума различающей информации (10) – уже сейчас могут служить надежной базой для отыскания экстремальных принципов в самых разных областях естественных и гуманитарных наук.
Особо следует сказать о перспективах обоснования формализма Джейнса. В современной науке возникли предпосылки – идеи и разработки – для возврата к программе Эйлера именно в форме принципа максимума энтропии. Любое формальное моделирование объектов науки основывается на подборе математической структуры, адекватно отражающей структуру и функционирование моделируемой системы. К концу ХХ столетия сформировалась область математического знания, позволяющая оперировать полными совокупностями одинаково структурированных множеств, а также устанавливать соответствия между классами структурированных объектов с различной аксиоматикой. Эта область – теория категорий и функторов – включает в себя и способы сравнения по степени “структурированности” различных состояний моделируемых систем. Другими словами, на самом общем уровне описание систем возникает конструктивная возможность рассчитывать числовые характеристики состояний и с помощью их выявлять экстремальные состояния системы [1, 13,14, 35, 36]. Указанная числовая характеристика есть число преобразований, допускаемых структурой системы, и может быть интерпретирована как количество микросостояний системы, соответствующее ее макросостоянию, т.е. как обобщенная энтропия системы. Таким образом появляется строгий метод расчета энтропии систем, поддающихся формальному описанию с помощью математических структур, и алгоритм порождения целевых функций для задач с использованием формализма Джейнса и других модификаций принципа максимума энтропии. Ряд современных теорем вариационного моделирования [15, 37] позволяет надеяться преодолеть и те трудности, которые связаны с произволом в выборе ограничивающих экстремум энтропии условий.
💥 Видео
Уравнения Лагранжа #1Скачать

Основы вариационного исчисления | уравнение Эйлера Лагранжа | конкретные примеры | 3Скачать
Основы вариационного исчисления | уравнение Эйлера Лагранжа | конкретные примеры | 1Скачать

Функция Лагранжа. Уравнения Лагранжа. Интегралы движения.Скачать

#Дифуры I. Урок 11. Уравнение Лагранжа . Уравнение КлероСкачать

Основы вариационного исчисления | уравнение Эйлера Лагранжа | конкретные примеры | 2Скачать
Основы вариационного исчисления | многомерные вариационные задачи | уравнение Эйлера ЛагранжаСкачать

Основы вариационного исчисления | конкретные Лагранжианы | 2 | классический одномерный осциляторСкачать

№10. Уравнения Лагранжа первого и второго рода. Общее уравнение динамики.Скачать

Т. Уравнения Лагранжа 2 рода. Теория.Скачать

Принцип наименьшего действия (Принцип Гамильтона)Скачать

Классические уравнения | математический маятник | вывод при помощи уравнения Эйлера - ЛагранжаСкачать