Вывод уравнения колебания математического маятника через закон сохранения энергии

О чем эта статья:

9 класс, 11 класс, ЕГЭ/ОГЭ

Видео:Математические и пружинные маятники. 11 класс.Скачать

Механические колебания

Механические колебания — это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени.

Колебания делятся на два вида: свободные и вынужденные.

Видео:математический маятник ЕГЭ ФИЗИКА колебания частота периодСкачать

Свободные колебания

Это колебания, которые происходят под действием внутренних сил в колебательной системе.

Они всегда затухающие, потому что весь запас энергии, сообщенный в начале, в конце уходит на совершение работы по преодолению сил трения и сопротивления среды (в этом случае механическая энергия переходит во внутреннюю). Из-за этого свободные колебания почти не имеют практического применения.

Видео:Вывод закона сохранения механической энергии | Физика 9 класс #22 | ИнфоурокСкачать

Вынужденные колебания

А вот вынужденные колебания восполняют запас энергии внешним воздействием. Если это происходит каждый период, то колебания вообще затухать не будут.

Вынужденные колебания — это колебания, которые происходят под действием внешней периодически меняющейся силы.

Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.

Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным.

Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием.

Видео:Классические уравнения | физический маятник | вывод при помощи уравнения Эйлера - ЛагранжаСкачать

Автоколебания

Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.

У автоколебательной системы есть три важных составляющих:

• сама колебательная система
• источник энергии
• устройство обратной связи, обеспечивающей связь между источником и системой

Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.

Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.

Видео:Математический маятник или откуда формула периодаСкачать

Характеристики колебаний

Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение можно описать величинами: период, частота, амплитуда, фаза колебаний.

Период — это время одного полного колебания. Измеряется в секундах и обозначается буквой T.

Формула периода колебаний

T = t/N

N — количество колебаний [—]

Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.

Формула частоты

ν = N/t = 1/T

N — количество колебаний [—]

Амплитуда — это максимальное отклонение от положения равновесия. Измеряется в метрах и обозначается либо буквой A, либо x max .

Она используется в уравнении гармонических колебаний:

Видео:Гармонические колебания. Вывод формул. Математический маятник. Пружинный маятник. LC-контурСкачать

Гармонические колебания

Простейший вид колебательного процесса — простые гармонические колебания, которые описывают уравнением:

Уравнение гармонических колебаний

x — координата в момент времени t [м]

t — момент времени [с]

(2πνt) в этом уравнении — это фаза. Ее обозначают греческой буквой φ

Фаза колебаний

t — момент времени [с]

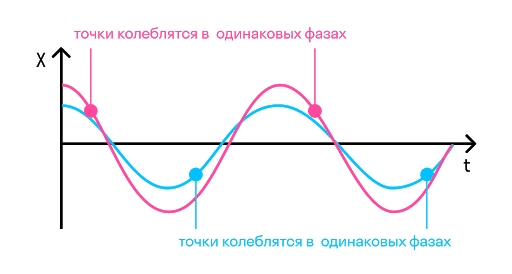
Фаза колебаний — это физическая величина, которая показывает отклонение точки от положения равновесия. Посмотрите на рисунок, на нем изображены одинаковые фазы:

Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу.

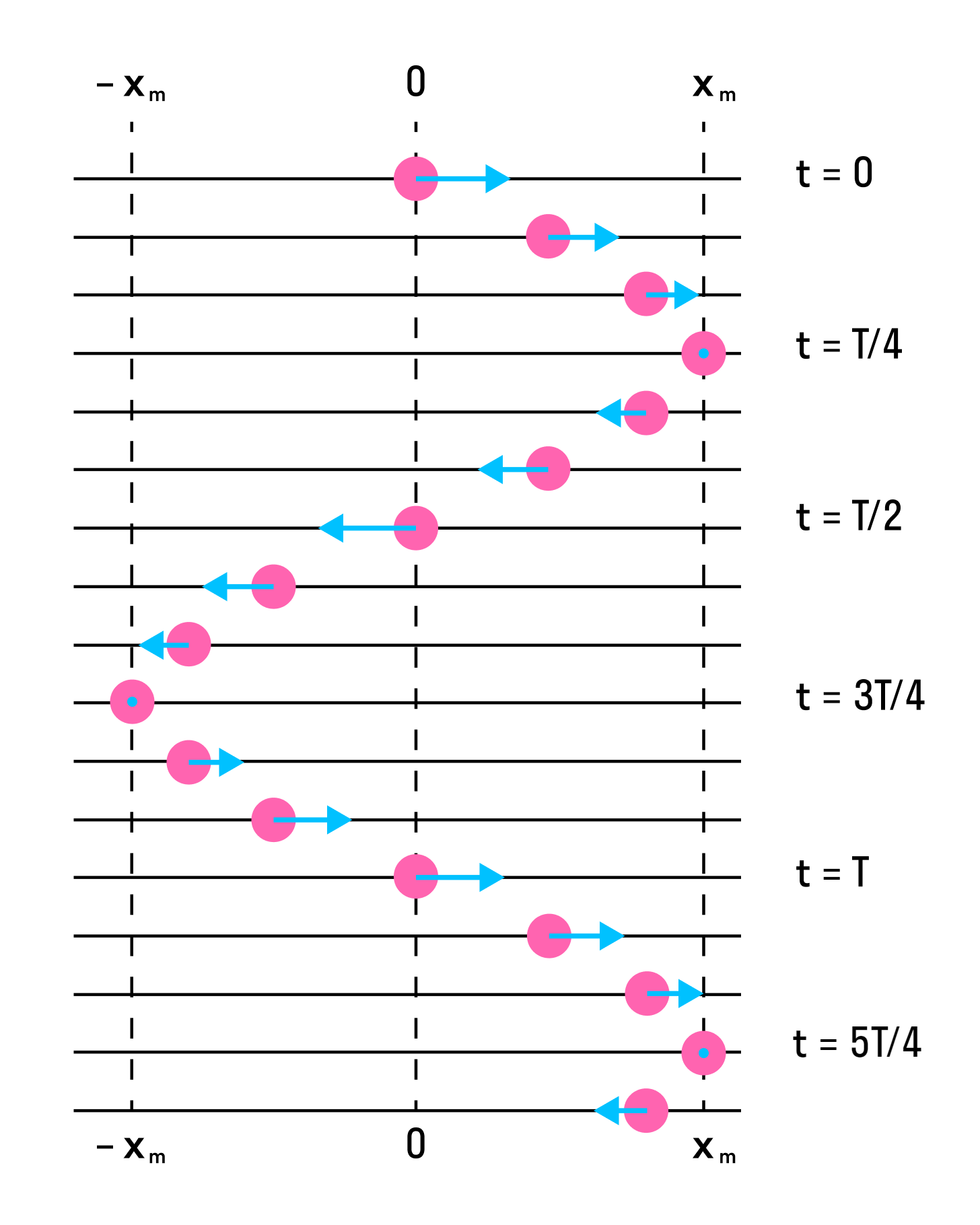
На рисунке ниже показаны положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.

Если изменить период, начальную фазу или амплитуду колебания, графики тоже изменятся.

На рисунке ниже во всех трех случаях для синих кривых начальная фаза равна нулю, а в последнем (с) — красная кривая имеет меньшую начальную фазу.

В первом случае (а) красная кривая описывает колебание, у которого амплитуда больше колебания, описанного синей линией.

Во втором случае (b) красная кривая отличается от синей только значением периода — у красной период в два раза меньше.

Видео:Колебания математического маятникаСкачать

Математический маятник

Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.

Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.

Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).

Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:

Формула периода колебания математического маятника

l — длина нити [м]

g — ускорение свободного падения [м/с 2 ]

На планете Земля g = 9,8 м/с 2

Видео:Видеоурок по физике "Математический и пружинный маятники"Скачать

Пружинный маятник

Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.

В пружинном маятнике колебания совершаются под действием силы упругости.
Пока пружина не деформирована, сила упругости на тело не действует.

Формула периода колебания пружинного маятника

m — масса маятника [кг]

k — жесткость пружины [Н/м]

Видео:Применение закона сохранения и превращения механической энергии. Практическая часть. 9 класс.Скачать

Закон сохранения энергии для гармонических колебаний

Физика — такая клевая наука, в которой ничего не исчезает бесследно и не появляется из ниоткуда. Эту особенность описывает закон сохранения энергии.

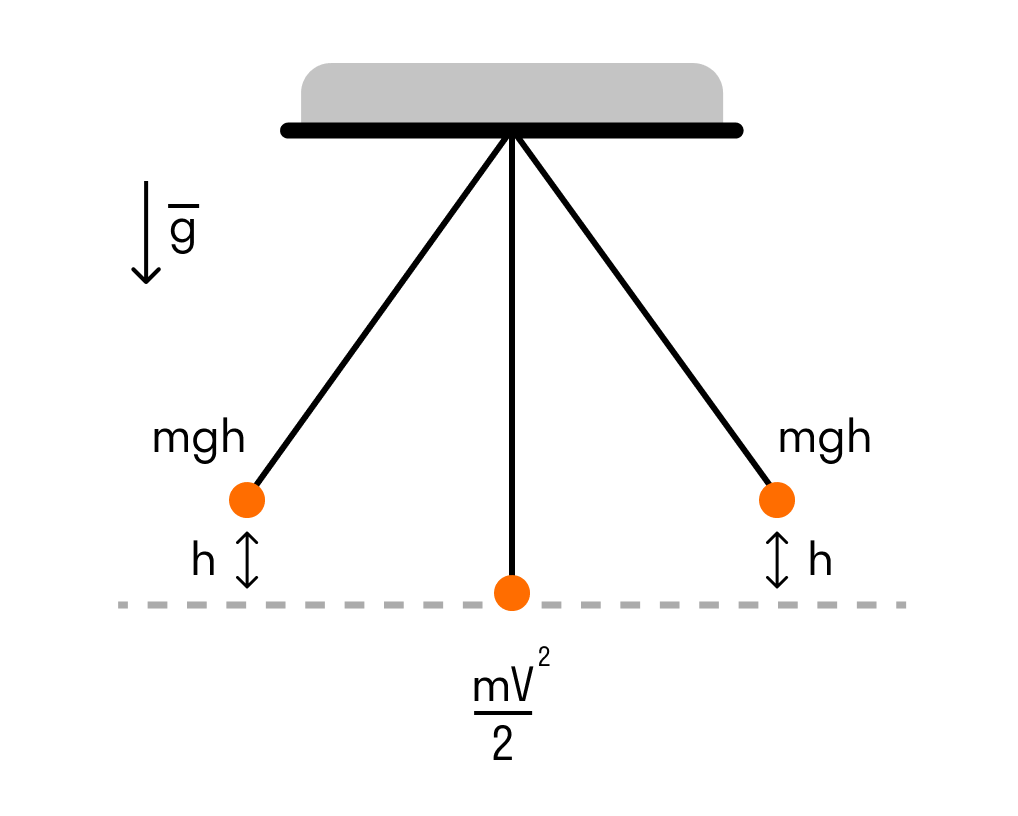
Рассмотрим его на примере математического маятника.

• Когда маятник отклоняют на высоту h, его потенциальная энергия максимальна.
• Когда маятник опускается, потенциальная энергия переходит в кинетическую. Причем в нижней точке, где потенциальная энергия равна нулю, кинетическая энергия максимальна и равна потенциальной энергии в верхней точке. Скорость груза в этой точке максимальна.

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!

Видео:Закон Сохранения Энергии // Урок по Физике 7 класс - Закон Сохранения Механической ЭнергииСкачать

Формулы математического маятника

Видео:Урок 122. Закон сохранения полной механической энергииСкачать

Определение и формулы математического маятника

Математический маятник — это колебательная система, являющаяся частным случаем физического маятника, вся масса которого сосредоточена в одной точке, центре масс маятника.

Обычно математический маятник представляют как шарик, подвешенный на длинной невесомой и нерастяжимой нити. Это идеализированная система, совершающая гармонические колебания под действием силы тяжести. Хорошим приближением к математическому маятнику массивный маленький шарик, осуществляющий колебания на тонкой длинной нити.

Галилей первым изучал свойства математического маятника, рассматривая качание паникадила на длинной цепи. Он получил, что период колебаний математического маятника не зависит от амплитуды. Если при запуске мятника отклонять его на разные малые углы, то его колебания будут происходить с одним периодом, но разными амплитудами. Это свойство получило название изохронизма.

Видео:Урок 92 (осн). Колебательное движение. МаятникиСкачать

Уравнение движения математического маятника

Математический маятник — классический пример гармонического осциллятора. Он совершает гармонические колебания, которые описываются дифференциальным уравнением:

где $varphi $ — угол отклонения нити (подвеса) от положения равновесия.

Решением уравнения (1) является функция $varphi (t):$

где $alpha $ — начальная фаза колебаний; $_0$ — амплитуда колебаний; $_0$ — циклическая частота.

Колебания гармонического осциллятора — это важный пример периодического движения. Осциллятор служит моделью во многих задачах классической и квантовой механики.

Видео:Классические уравнения | математический маятник | вывод через второй закон НьютонаСкачать

Циклическая частота и период колебаний математического маятника

Циклическая частота математического маятника зависит только от длины его подвеса:

Период колебаний математического маятника ($T$) в этом случае равен:

Выражение (4) показывает, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения.

Видео:Колебания математического и пружинного маятников. 9 класс.Скачать

Уравнение энергии для математического маятника

При рассмотрении колебаний механических систем с одной степенью свободы часто берут в качестве исходного не уравнения движения Ньютона, а уравнение энергии. Так как его проще составлять, и оно является уравнением первого порядка по времени. Предположим, что трение в системе отсутствует. Закон сохранения энергии для совершающего свободные колебания математического маятника (колебания малые) запишем как:

где $E_k$ — кинетическая энергия маятника; $E_p$ — потенциальная энергия маятника; $v$ — скорость движения маятника; $x$ — линейное смещение груза маятника от положения равновесия по дуге окружности радиуса $l$, при этом угол — смещение связан с $x$ как:

Максимальное значение потенциальной энергии математического маятника равно:

Максимальная величина кинетической энергии:

где $h_m$ — максимальная высота подъема маятника; $x_m$- максимальное отклонение маятника от положения равновесия; $v_m=_0x_m$ — максимальная скорость.

Видео:Превращение энергии при колебаниях. Уравнение колебательного движения. 1 часть. 9 класс.Скачать

Примеры задач с решением

Задание. Какова максимальная высота подъема шарика математического маятника, если его скорость движения при прохождении положения равновесия составляла $v$?

Решение. Сделаем рисунок.

Пусть ноль потенциальной энергии шарика в его положении равновесия (точка 0).В этой точке скорость шарика максимальна и равна по условию задачи $v$. В точке максимального подъема шарика над положением равновесия (точка A), скорость шарика равна нулю, потенциальная энергия максимальна. Запишем закон сохранения энергии для рассмотренных двух положений шарика:

Из уравнения (1.1) найдем искомую высоту:

Ответ. $h=frac$

Задание. Каково ускорение силы тяжести, если математический маятник имеющий длину $l=1 м$, совершает колебания с периодом равным $T=2 с$? Считайте колебания математического маятника малыми.textit

Решение. За основу решения задачи примем формулу для вычисления периода малых колебаний:

Выразим из нее ускорение:

Проведем вычисления ускорения силы тяжести:

Ответ. $g=9,87 frac$

Видео:Закон сохранения энергии. 9 класс. Решение задачСкачать

1.1. Уравнение гармонических колебаний

В этом разделе мы покажем, что уравнения колебательного движения многих систем, в сущности, одинаковы, так что различные физические процессы могут быть описаны одними и теми же математическими формулами.

Пружинный маятник — это система, состоящая из шарика массой m, подвешенного на пружине длиной .

Рис. 1.2. К выводу уравнения движения для пружинного маятника

В положении равновесия (рис. 1.2) сила тяжести уравновешивается упругой силой :

где – статическое удлинение пружины. Направим ось x вниз и выберем начало отсчета так, что координата x = 0 соответствует положению неподвижного шарика в положении равновесия.

Если теперь оттянуть шарик от положения равновесия на расстояние x, то полное удлинение пружины станет равным . По закону Гука проекция результирующей силы на ось ОХ будет тогда равна

Знак минус означает, что сила стремится уменьшить отклонение от положения равновесия. Полученное выражение соответствует упругой силе слабо деформированной пружины.

Запишем теперь уравнение второго закона Ньютона:

Его можно также представить в виде:

Математический маятник

Математический маятник — это идеализированная система, состоящая из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке.

Будем характеризовать отклонение маятника от положения равновесия углом , который образует нить с вертикалью (рис. 1.3).

Рис. 1.3. К выводу уравнения движения математического маятника

При отклонении маятника от положения равновесия на материальную точку массой m действуют сила тяжести и сила натяжения нити . Соответственно, уравнение движения этой материальной точки имеет вид

.

Проецируя его на направления нормали и касательной к траектории (окружности радиуса ), получаем

Модуль скорости равен , учитывая, что при движении точки к положению равновесия угол убывает, а скорость точки растет, напишем

.

Тогда второе из написанных выше уравнений движения приобретает вид

При малых отклонениях маятника от вертикали, когда ,

Физический маятник

Физический маятник — это протяженное колеблющееся тело, закрепленное на оси. Его размеры таковы, что его невозможно рассматривать как материальную точку.

Пример физического маятника приведен на рис. 1.4.

Рис. 1.4. К выводу уравнения движения физического маятника

При отклонении маятника от положения равновесия на угол возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен

где m – масса маятника, а l – расстояние 0C между точкой подвеса 0 и центром масс C маятника.

Рассматривая как вектор, связанный с направлением поворота правилом правого винта, противоположность знаков и можно объяснить тем, что векторы и направлены в противоположные стороны. Обозначив момент инерции маятника относительно оси, проходящей через точку подвеса, как I, для маятника можно записать основное уравнение динамики вращательного движения:

Ограничимся рассмотрением малых отклонений от положения равновесия:

В этом случае уравнение колебаний принимает вид:

В случае, когда физический маятник можно представить как материальную точку, колеблющуюся на нити длиной l, момент инерции равен

и мы приходим к уравнению (1.6) движения математического маятника.

Колебания поршня в сосуде с идеальным газом

Рассмотрим цилиндр с площадью поперечного сечения , в который вставлен поршень массы (рис. 1.5). Под поршнем в цилиндре идеальный газ с показателем адиабаты , над поршнем воздух с постоянным (атмосферным) давлением . Поршень может двигаться в цилиндре вверх и вниз без трения. Будем считать, что в равновесии объем идеального газа под поршнем равен и изменения объема газа, обусловленные движением поршня, происходят адиабатно, то есть без теплообмена со стенками цилиндра и поршнем.

Рис. 1.5. Колебания поршня, закрывающего сосуд с идеальным газом

В состоянии равновесия давление в газе под поршнем складывается из атмосферного давления и давления , оказываемого поршнем. Обозначим это результирующее давление :

Переместим поршень на расстояние x вверх. Объем сосуда увеличится и станет равным

Соответственно уменьшится давление. В силу предположения об отсутствии теплообмена, новое давление в газе можно найти из уравнения адиабаты Пуассона

Здесь — показатель адиабаты, зависящий от числа степеней свободы молекул газа.

При малых колебаниях, когда изменение объема газа много меньше его «равновесной» величины , то есть когда

выражение (1.11) можно разложить в ряд Тейлора:

На поршень действуют три силы: сила атмосферного давления , сила давления газа под поршнем и сила тяжести . Знаки сил соответствуют выбору положительного направления оси x вверх. Используя (1.10) и (1.12), находим для равнодействующей этих сил:

Используя (1.13), уравнение движения поршня

Видео:ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ в механике класс физика ПерышкинСкачать

Математический маятник: период, ускорение и формулы

Механическая система, которая состоит из материальной точки (тела), висящей на нерастяжимой невесомой нити (ее масса ничтожно мала по сравнению с весом тела) в однородном поле тяжести, называется математическим маятником (другое название – осциллятор). Бывают и другие виды этого устройства. Вместо нити может быть использован невесомый стержень. Математический маятник может наглядно раскрыть суть многих интересных явлений. При малой амплитуде колебания его движение называется гармоническим.

Видео:Урок 126. Задачи на закон сохранения энергии (ч.1)Скачать

Общие сведения о механической системе

Если маятник находится в положении равновесия (висит отвесно), то сила тяжести будет уравновешиваться силой натяжения нити. Плоский маятник на нерастяжимой нити является системой с двумя степенями свободы со связью. При смене всего одного компонента меняются характеристики всех ее частей. Так, если нитку заменить на стержень, то у данной механической системы будет всего 1 степень свободы. Какими же свойствами обладает математический маятник? В этой простейшей системе под воздействием периодического возмущения возникает хаос. В том случае, когда точка подвеса не двигается, а совершает колебания, у маятника появляется новое положение равновесия. При быстрых колебаниях вверх-вниз эта механическая система приобретает устойчивое положение «вверх тормашками». У нее есть и свое название. Ее называют маятником Капицы.

Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Свойства маятника

• Если, сохраняя одинаковую длину маятника, подвешивать различные грузы, то период их колебаний получится одинаковым, хотя их массы будут сильно различаться. Следовательно, период такого маятника не зависит от массы груза.

• Если при запуске системы отклонять маятник на не слишком большие, но разные углы, то он станет колебаться с одинаковым периодом, но по разным амплитудам. Пока отклонения от центра равновесия не слишком велики, колебания по своей форме будут достаточно близки гармоническим. Период такого маятника никак не зависит от колебательной амплитуды. Это свойство данной механической системы называется изохронизмом (в переводе с греческого «хронос» — время, «изос» — равный).

Видео:Урок 327. Гармонические колебанияСкачать

Период математического маятника

Этот показатель представляет собой период собственных колебаний. Несмотря на сложную формулировку, сам процесс очень прост. Если длина нити математического маятника L, а ускорение свободного падения g, то эта величина равна:

Период малых собственных колебаний ни в какой мере не зависит от массы маятника и амплитуды колебаний. В этом случае маятник двигается как математический с приведенной длиной.

Колебания математического маятника

Математический маятник совершает колебания, которые можно описать простым дифференциальным уравнением:

где х (t) – неизвестная функция (это угол отклонения от нижнего положения равновесия в момент t, выраженный в радианах); ω – положительная константа, которая определяется из параметров маятника (ω = √g/L, где g – это ускорение свободного падения, а L – длина математического маятника (подвес).

Уравнение малых колебаний вблизи положення равновесия (гармоническое уравнение) выглядит так:

Колебательные движения маятника

Математический маятник, который совершает малые колебания, двигается по синусоиде. Дифференциальное уравнение второго порядка отвечает всем требованиям и параметрам такого движения. Для определения траектории необходимо задать скорость и координату, из которых потом определяются независимые константы:

где θ₀ – начальная фаза, A – амплитуда колебания, ω – циклическая частота, определяемая из уравнения движения.

Математический маятник (формулы для больших амплитуд)

Данная механическая система, совершающая свои колебания со значительной амплитудой, подчиняется более сложным законам движения. Для такого маятника они рассчитываются по формуле:

sin x/2 = u * sn(ωt/u),

где sn — синус Якоби, который для u 2 августа, 2014