Вывод основного уравнения динамики вращательного движения из уравнения моментов

Для кинематического описания процесса вращения твердого тела нужно ввести такие понятия как угловое перемещение Δ φ , угловое ускорение ε и угловая скорость ω :

ω = ∆ φ ∆ t , ( ∆ t → 0 ) , ε = ∆ φ ∆ t , ( ∆ t → 0 ) .

Углы выражаются в радианах. За положительное направление вращения принимается направление против часовой стрелки.

Когда твердое тело вращается относительно неподвижной оси, все точки этого тела перемещаются с одинаковыми угловыми скоростями и ускорениями.

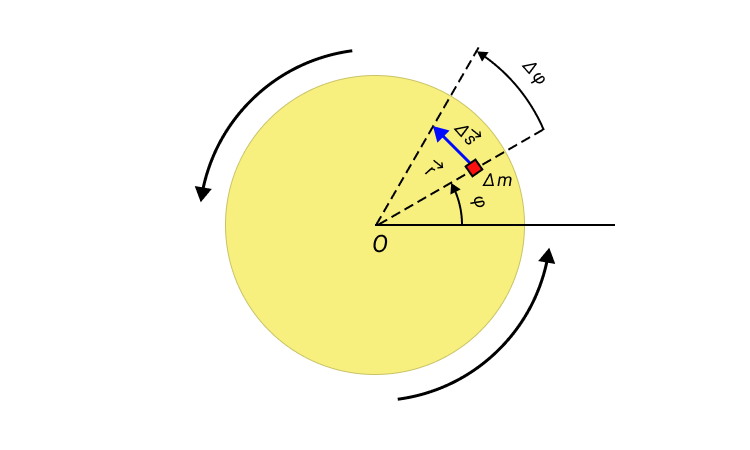
Рисунок 1. Вращение диска относительно оси, проходящей через его центр O .

Если угловое перемещение Δ φ мало, то модуль вектора линейного перемещения ∆ s → некоторого элемента массы Δ m вращающегося твердого тела можно выразить соотношением:

в котором r – модуль радиус-вектора r → .

Между модулями угловой и линейной скоростей можно установить связь посредством равенства

Модули линейного и углового ускорения также взаимосвязаны:

Векторы v → и a → = a τ → направлены по касательной к окружности радиуса r .

Также нам необходимо учесть возникновение нормального или центростремительного ускорения, которое всегда возникает при движении тел по окружности.

Модуль ускорения выражается формулой:

a n = v 2 r = ω 2 r .

Если разделить вращающееся тело на небольшие фрагменты Δ m i , обозначить расстояние до оси вращения через r i , а модули линейных скоростей через v i , то запись формулы кинестетической энергии вращающегося тела будет иметь вид:

E k = ∑ i ν m v i 2 2 = ∑ i ∆ m ( r i ω ) 2 2 = ω 2 2 ∑ i ∆ m i r i 2 .

Физическая величина ∑ i ∆ m i r i 2 носит название момента инерции I тела относительно оси вращения. Она зависит от распределения масс вращающегося тела относительно оси вращения:

I = ∑ i ∆ m i r i 2 .

В пределе при Δ m → 0 эта сумма переходит в интеграл. Единица измерения момента инерции в С И – килограмм—метр в квадрате ( к г · м 2 ) . Таким образом, кинетическую энергию твердого тела, вращающегося относительно неподвижной оси, можно представить в виде:

В отличие от выражения, которое мы использовали для описания кинестетической энергии поступательно движущегося тела m v 2 2 , вместо массы m в формулу входит момент инерции I . Также мы принимаем во внимание вместо линейной скорости v угловую скорость ω .

Если для динамики поступательного движения основную роль играет масса тела, то в динамике вращательного движения имеет значение момент инерции. Но если масса – это свойство рассматриваемого твердого тела, которое не зависит от скорости движения и других факторов, то момент инерции зависит от того, вокруг какой оси вращается тело. Для одного и того же тела момент инерции будет определяться различными осями вращения.

В большинстве задач считается, что ось вращения твердого тела проходит через центр его массы.

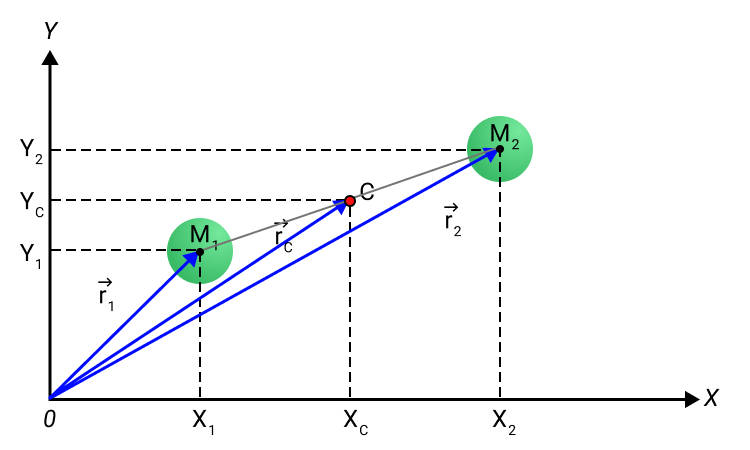
Положение x C , y C центра масс для простого случая системы из двух частиц с массами m 1 и m 2 , расположенными в плоскости X Y в точках с координатами x 1 , y 1 и x 2 , y 2 определяется выражениями:

x C = m 1 x 1 + m 2 x 2 m 1 + m 2 , y C = m 1 y 1 + m 2 y 2 m 1 + m 2 .

Рисунок 2. Центр масс C системы из двух частиц.

В векторной форме это соотношение принимает вид:

r C → = m 1 r 1 → + m 2 r 2 → m 1 + m 2 .

Аналогично, для системы из многих частиц радиус-вектор r C → центра масс определяется выражением

r C → = ∑ m i r i → ∑ m i .

Если мы имеем дело с твердым телом, состоящим из одной части, то в приведенном выражении суммы для r C → необходимо заменить интегралами.

Центр масс в однородном поле тяготения совпадает с центром тяжести. Это значит, что если мы возьмем тело сложной формы и подвесим его за центр масс, то в однородном поле тяготения это тело будет находиться в равновесии. Отсюда следует способ определения центра масс сложного тела на практике: его необходимо последовательно подвесить за несколько точек, одновременно отмечая по отвесу вертикальные линии.

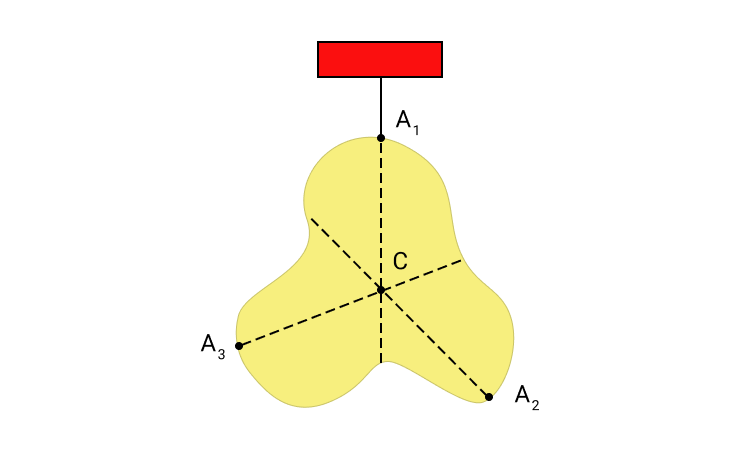
Рисунок 3. Определение положения центра масс C тела сложной формы. A 1 , A 2 , A 3 точки подвеса.

На рисунке мы видим тело, которое подвешено за центр масс. Оно находится в состоянии безразличного равновесия. В однородном поле тяготения равнодействующая сил тяжести приложена к центру масс.

Мы можем представить любое движение твердого тела как сумму двух движений. Первое поступательное, которое производится со скоростью центра масс тела. Второе – это вращение относительно оси, которая проходит через центр масс.

Предположим. Что у нас есть колесо, которое катится по горизонтальной поверхности без проскальзывания. Все точки колеса во время движения перемещаются параллельно одной плоскости. Такое движение мы можем обозначить как плоское.

Видео:Урок 93. Основное уравнение динамики вращательного движенияСкачать

Теорема о движении центра масс

Кинестетическая энергия вращающегося твердого тела при плоском движении будет равна сумме кинетической энергии поступательного движения и кинетической энергии вращения относительно оси, которая проведена через центр масс и располагается перпендикулярно плоскостям, в которых движутся все точки тела:

E k = m v C 2 2 + I C ω 2 2 ,

где m – полная масса тела, I C – момент инерции тела относительно оси, проходящей через центр масс.

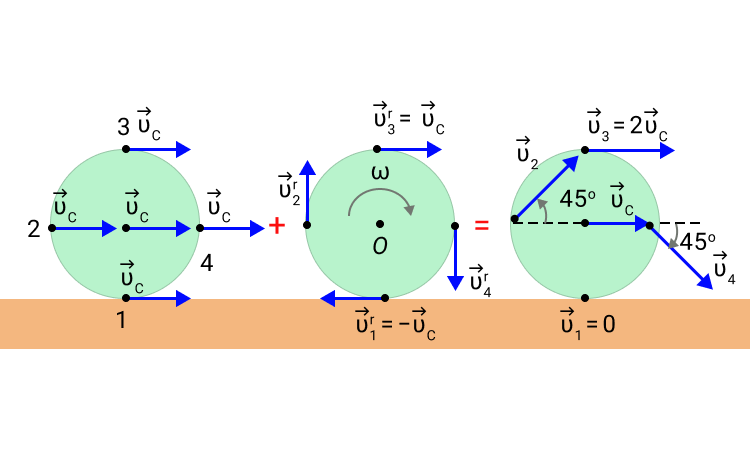
Рисунок 4. Качение колеса как сумма поступательного движения со скоростью v C → и вращения с угловой скоростью ω = v C R относительно оси O , проходящей через центр масс.

В механике используется теорема о движении центра масс.

Любое тело или несколько взаимодействующих тел, которые представляют собой единую систему, обладают центром масс. Этот центр масс под воздействием внешних сил перемещается в пространстве как материальная точка, в которой сосредоточена вся масса системы.

На рисунке мы изобразили движение твердого тела, на которое действуют силы тяжести. Центр масс тела движется по траектории, которая близка к параболе, тогда как траектория остальных точек тела является более сложной.

Рисунок 5. Движение твердого тела под действием силы тяжести.

Видео:Физика. 10 класс. Основное уравнение динамики вращательного движенияСкачать

Теорема Штейнера о параллельном переносе оси вращения

Рассмотрим случай, когда твердое тело движется вокруг некоторой неподвижной оси. Момент инерции этого тела инерции I можно выразить через момент инерции I C этого тела относительно оси, проходящей через центр масс тела и параллельной первой.

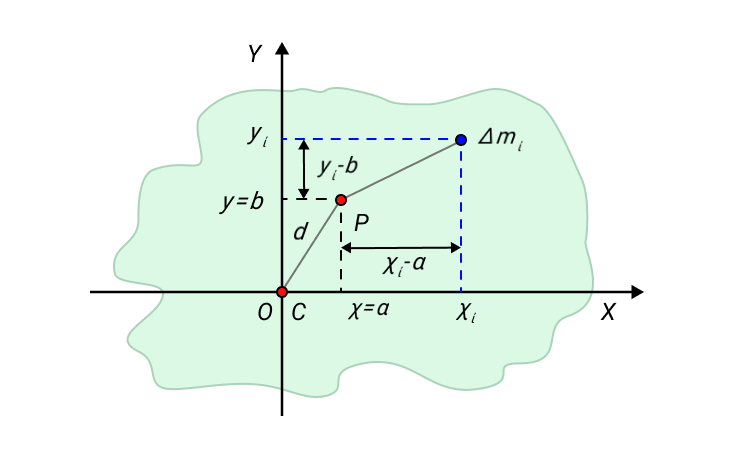
Рисунок 6. К доказательству теоремы о параллельном переносе оси вращения.

Для примера возьмем твердое тело, форма которого произвольна. Обозначим центр масс С . Выберем систему координат Х У с началом координат 0 . Совместим центр масс и начало координат.

Одна из осей проходит через центр масс С . Вторая ось пересекает произвольно выбранную точку Р , которая расположена на расстоянии d от начала координат. Выделим некоторый малый элемент массы данного твердого тела Δ m i .

По определению момента инерции:

I C = ∑ ∆ m i ( x i 2 + y i 2 ) , I P = ∑ m i ( x i — a ) 2 + y i — b 2

Выражение для I P можно переписать в виде:

I P = ∑ ∆ m i ( x i 2 + y i 2 ) + ∑ ∆ m i ( a 2 + b 2 ) — 2 a ∑ ∆ m i x i — 2 b ∑ ∆ m i y i .

Два последних члена уравнения обращаются в нуль, так как начало координат в нашем случае совпадает с центром масс тела.

Так мы пришли к формуле теоремы Штейнера о параллельном переносе оси вращения.

Для тела, которое вращается относительно произвольной неподвижной оси, момент инерции, согласно теореме Штейнера, равен сумме момента инерции этого тела относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями.

I P = I C + m d 2 ,

где m – полная масса тела.

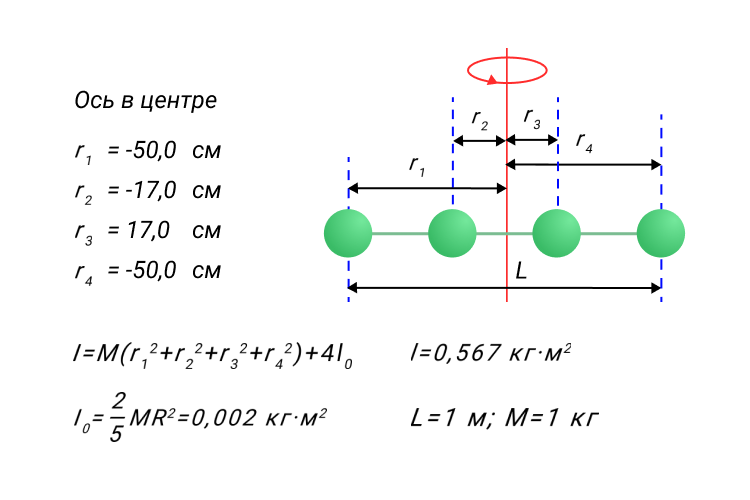
Рисунок 7. Модель момента инерции.

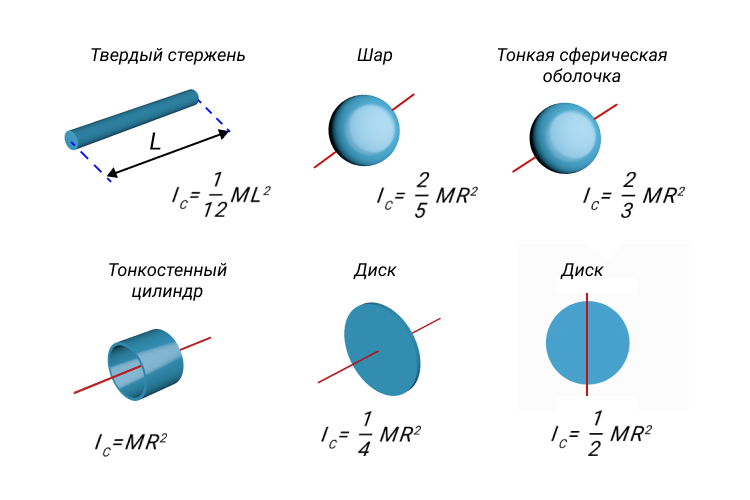
На рисунке ниже изображены однородные твердые тела различной формы и указаны моменты инерции этих тел относительно оси, проходящей через центр масс.

Рисунок 8. Моменты инерции I C некоторых однородных твердых тел.

Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

Основное уравнение динамики вращательного движения твердого тела

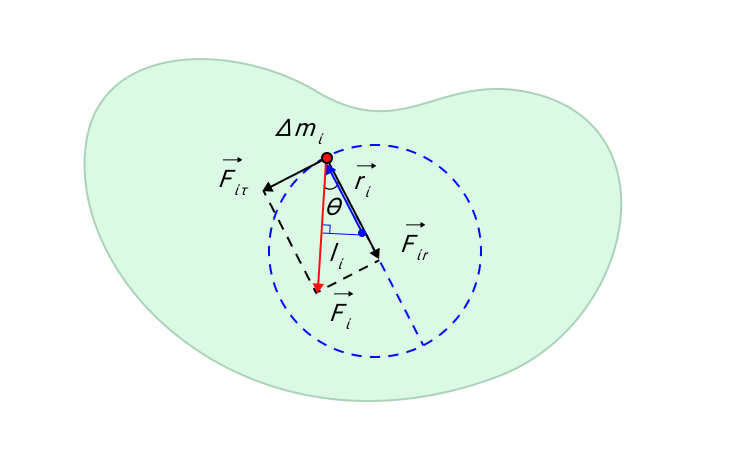
В тех случаях, когда мы имеем дело с твердым телом, которое вращается относительно неподвижной оси, мы можем обобщить второй закон Ньютона. На рисунке ниже мы изобразили твердое тело произвольной формы, вращающееся относительно некоторой оси, проходящей через точку О . Ось вращения расположена перпендикулярно плоскости рисунка.

Δ m i – это произвольный малый элемент массы, на который оказывают воздействие внешние и внутренние силы. Равнодействующая всех сил есть F i → . Ее можно разложить на две составляющие: касательную составляющую F i τ → и радиальную F i r → . Радиальная составляющая F i r → создает центростремительное ускорение a n .

Рисунок 9. Касательная F i τ → и радиальная F i r → составляющие силы F i → действующей на элемент Δ m i твердого тела.

Касательная составляющая F i τ → вызывает тангенциальное ускорение a i τ → массы Δ m i . Второй закон Ньютона, записанный в скалярной форме, дает

∆ m i a i τ = F i τ sin θ или ∆ m i r i ε = F i sin θ ,

где ε = a i τ r i – угловое ускорение всех точек твердого тела.

Если обе части написанного выше уравнения умножить на r i , то мы получим:

∆ m i r i 2 ε = F i r i sin θ = F i l i = M i .

Здесь l i – плечо силы, F i , → M i – момент силы.

Теперь нужно аналогичные соотношения записать для всех элементов массы Δm_i вращающегося твердого тела, а затем просуммировать левые и правые части. Это дает:

∑ ∆ m i r i 2 ε = ∑ M i .

Стоящая в правой части сумма моментов сил, действующих на различные точки твердого тела, состоит из суммы моментов всех внешних сил и суммы моментов всех внутренних сил.

∑ M = ∑ M i в н е ш н + ∑ M i в н у т р .

Но сумма моментов всех внутренних сил согласно третьему закону Ньютона равна нулю, поэтому в правой части остается только сумма моментов всех внешних сил, которые мы будем обозначать через M . Так мы получили основное уравнение динамики вращательного движения твердого тела.

Угловое ускорение ε и момент сил M в этом уравнении являются величинами алгебраическими.

Обычно за положительное направление вращения принимают направление против часовой стрелки.

Возможна и векторная форма записи основного уравнения динамики вращательного движения, при которой величины ω → , ε → , M → определяются как векторы, направленные по оси вращения.

Видео:ЛР "Проверка основного уравнения динамики вращательного движения с помощью маятника Обербека"Скачать

Закон сохранения момента импульса

В разделе, посвященном поступательному движению тела, мы ввели понятие импульса тела p → . По аналогии с поступательным движением для вращательного движения мы вводим понятие момента импульса.

Момент импульса вращающегося тела – это физическая величина, которая равняется произведению момента инерции тела I на угловую скорость ω его вращения.

Для обозначения момента импульса используется латинская буква L .

Поскольку ε = ∆ ω ∆ t ; ∆ t → 0 , уравнение вращательного движения можно представить в виде:

M = I ε = I ∆ ω ∆ t или M ∆ t = I ∆ ω = ∆ L .

M = ∆ L ∆ t ; ( ∆ t → 0 ) .

Мы получили это уравнение для случая, когда I = c o n s t . Но оно будет справедливо и тогда, когда момент инерции тела будет изменяться в процессе движения.

Если суммарный момент M внешних сил, действующих на тело, равен нулю, то момент импульса L = I ω относительно данной оси сохраняется: ∆ L = 0 , если M = 0 .

L = l ω = c o n s t .

Так мы пришли к закону сохранения момента импульса.

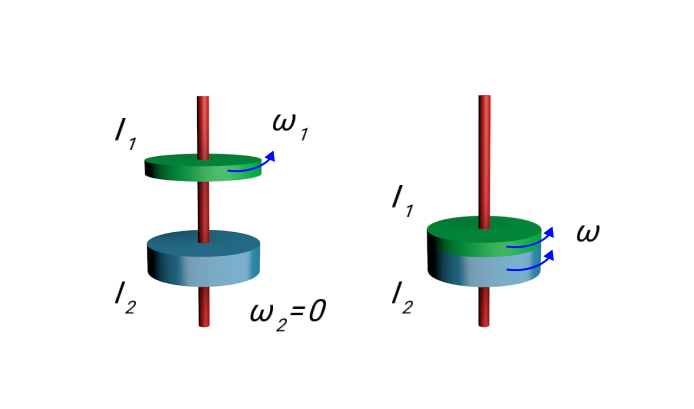
В качестве примера приведем рисунок, на котором изображено неупругое вращательное столкновение дисков, которые насажены на общую для них ось.

Рисунок 10. Неупругое вращательное столкновение двух дисков. Закон сохранения момента импульса: I 1 ω 1 = ( I 1 + I 2 ) ω .

Мы имеем дело с замкнутой системой. Для любой замкнутой системы закон сохранения момента импульса будет справедливым. Он выполняется и в условиях экспериментов по механике, и в условиях космоса, когда планеты движутся по своим орбитам вокруг звезды.

Мы можем записать уравнение динамики вращательного движения как для неподвижной оси, так и для оси, которая перемещается равномерно или с ускорением. Вид уравнения не изменится и в том случае, если ось движется ускоренно. Для этого должно выполняться два условия: ось должна проходить через центр массы тела, а ее направление в пространстве остается неизменным.

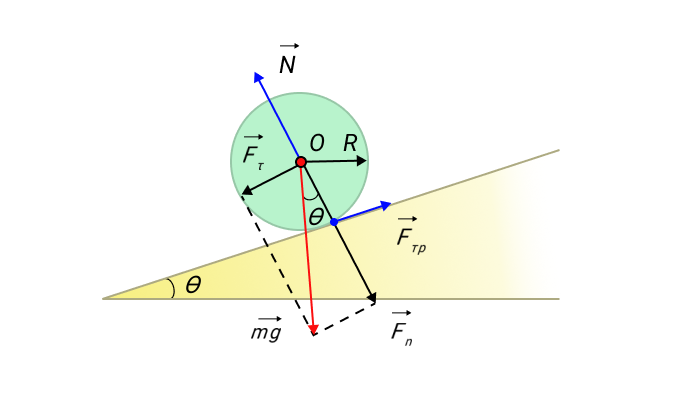
Предположим, что у нас есть тело (шар или цилиндр), которое катится по наклонной плоскости с некоторым трением.

Рисунок 11. Качение симметричного тела по наклонной плоскости.

Ось вращения O проходит через центр масс тела. Моменты силы тяжести m g → и силы реакции N → относительно оси O равны нулю. Момент M создает только сила трения: M = F т р R .

Уравнение вращательного движения:

I C ε = I C a R = M = F т р R ,

где ε – угловое ускорение катящегося тела, a – линейное ускорение его центра масс, I C – момент инерции относительно оси O , проходящей через центр масс.

Второй закон Ньютона для поступательного движения центра масс записывается в виде:

m a = m g sin α — F т р .

Исключая из этих уравнений F т р , получим окончательно:

α = m g sin θ I C R 2 + m .

Из этого выражения видно, что быстрее будет скатываться с наклонной плоскости тело, обладающее меньшим моментом инерции. Например, у шара I C = 2 5 m R 2 , а у сплошного однородного цилиндра I C = 1 2 m R 2 . Следовательно, шар будет скатываться быстрее цилиндра.

Видео:Лекция 06 Динамика твердого телаСкачать

§ 7.7. Основное уравнение динамики вращательного движения твердого тела

Уравнение движения

Для вывода основного уравнения динамики вращательного движения можно поступить следующим образом. Разделить мысленно тело на отдельные, достаточно малые элементы, которые можно было бы рассматривать как материальные точки (рис. 7.33). Записать для каждого элемента уравнение (7.6.13), и все эти уравнения почленно сложить. При этом внутренние силы, действующие между отдельными элементами, в уравнение движения тела не войдут. Сумма их моментов в результате сложения уравнений окажется равной нулю, так как по третьему закону Ньютона силы взаимодействия равны по модулю и направлены вдоль одной прямой в противоположные стороны. Учитывая далее, что при вращении твердого тела все его точки совершают одинаковые угловые перемещения с одинаковыми скоростями и ускорениями, можно таким образом получить уравнение вращательного движения всего тела.

Однако вывод этого уравнения довольно громоздок, поэтому мы на нем останавливаться не будем. Тем более что это уравнение имеет такую же форму, что и уравнение (7.6.13) для материальной точки, движущейся по окружности:

В этом уравнении Jω = L — момент импульса тела, а — суммарный момент всех внешних сил, действующих на тело относительно оси вращения.

Читается уравнение (7.7.1) так: производная по времени от момента импульса равна суммарному моменту внешних сил.

Следует иметь в виду, что вращение тела вокруг оси могут вызывать лишь силы i, лежащие в плоскости, перпендикулярной оси вращения (рис. 7.34). Силы же k, направленные параллельно оси вращения, очевидно, способны вызвать лишь перемещение тела вдоль оси. Момент каждой силы _i равен взятому со знаком плюс или минус произведению модуля этой силы на плечо d, т. е. на длину отрезка перпендикуляра, опущенного из точки С оси на линию действия силы _i:

Момент силы, вращающий тело вокруг данной оси против часовой стрелки, считается положительным, а по часовой стрелке — отрицательным.

Момент инерции тела

В формулу (7.7.1) входит момент инерции тела J. Момент инерции тела J равен сумме моментов инерции AJ₁ отдельных малых элементов, на которые можно разбить все тело:

Так как момент инерции материальной точки

где Δm₁; — масса элемента тела, a r₁ — его расстояние до оси вращения (см. рис. 7.33), то

Момент инерции тела зависит не только от массы тела, но и от характера распределения этой массы. Чем больше вытянуто тело вдоль оси вращения, тем меньше его момент инерции, так как тем ближе к оси вращения расположены отдельные элементы тела. Очевидно также, что, изменив ось вращения тела, мы тем самым изменим и его момент инерции. У твердых тел момент инерции относительно данной оси — постоянная величина. Поэтому изменение момента импульса может происходить лишь за счет изменения угловой скорости. Соответственно уравнение (7.7.1) можно записать в виде:

Читается это уравнение так: произведение момента инерции тела относительно оси вращения на угловое ускорение тела равно сумме моментов (относительно той же оси) всех внешних сил, приложенных к телу.

Уравнение (7.7.6) показывает, что при вращении тела момент инерции играет роль массы, момент силы — роль силы, а угловое ускорение — роль линейного ускорения при движении материальной точки или центра масс.

В том, что угловое ускорение определяется действительно моментом силы, т. е. силой и плечом, а не просто силой, убедиться нетрудно. Так, раскрутить велосипедное колесо до одной и той же угловой скорости одной и той же силой (например, усилием пальца) можно гораздо быстрее, если прикладывать силу к ободу колеса (это создает больший момент), а не к спицам вблизи втулки (рис. 7.35).

Для того чтобы убедиться в том, что угловое ускорение определяется именно моментом инерции, а не массой тела, нужно иметь в распоряжении тело, форму которого можно легко изменять, не меняя массы. Велосипедное колесо здесь непригодно. Но можно воспользоваться своим собственным телом. Попробуйте закрутиться на пятке, оттолкнувшись от пола другой ногой. Если вы при этом прижмете руки к груди, то угловая скорость окажется большей, чем если вы раскинете руки в стороны. Эффект будет особенно заметным, если в обе руки взять по толстой книге.

Моменты инерции обруча и цилиндра

Найти момент инерции тела произвольной несимметричной формы довольно сложно. Проще его измерить опытным путем, чем вычислить.

Мы ограничимся вычислением момента инерции тонкого обруча, вращающегося вокруг оси, проходящей через его центр. Если масса колеса сосредоточена главным образом в его ободе (как, например, у велосипедного колеса), то такое колесо приближенно можно рассматривать как обруч, пренебрегая массой спиц и втулки.

Разобьем обруч на N одинаковых элементов. Если m — масса всего обруча, то масса каждого элемента . Толщину обруча будем считать много меньшей ее радиуса (рис. 7.36). Если число элементов выбрать достаточно большим, то каждый элемент можно рассматривать как материальную точку. Поэтому момент инерции произвольного элемента с номером i будет равен:

Подставляя выражение (7.7.7) в формулу (7.7.5) для полного момента инерции, получим:

Здесь мы учли, что расстояние R для всех элементов одинаково и что сумма масс элементов равна массе m обруча.

Получился очень простой результат: момент инерции обруча равен произведению его массы на квадрат радиуса. Момент инерции обруча данной массы тем больше, чем больше его радиус. Формула (7.7.8) определяет также момент инерции полого тонкостенного цилиндра при его вращении вокруг оси симметрии.

Вычисление момента инерции сплошного однородного цилиндра массой m и радиусом R относительно его оси симметрии представляет более сложную задачу. Мы приведем лишь результат расчета:

Следовательно, если сравнить моменты инерции двух цилиндров одинакового размера и массы, один из которых полый, а другой сплошной, то у второго цилиндра момент инерции будет в два раза меньше. Это связано с тем, что у сплошного цилиндра масса расположена в среднем ближе к оси вращения.

Мы познакомились с уравнением вращательного движения твердого тела. По форме оно похоже на уравнение для поступательного движения твердого тела. Дано определение новых физических величин, характеризующих твердое тело: момента инерции и момента импульса.

Видео:7.2 Применение основного уравнения динамики вращательного движения. Школьная задача.Скачать

Основное уравнение динамики вращательного движения

Средняя оценка: 4.8

Всего получено оценок: 150.

Средняя оценка: 4.8

Всего получено оценок: 150.

Движение, при котором траектории точек твердого тела представляют собой окружности различных радиусов с центрами, лежащими на одной прямой, называется вращательным движением. Причины движения, в том числе вращательного, изучает динамика. Рассмотрим основное уравнение динамики вращательного движения твердого тела.

Видео:Физика. 10 класс. Основное уравнение динамики вращательного движения /05.10.2020/Скачать

Основное уравнение динамики

Динамика – это раздел механики, изучающий причины движения тел. Основным уравнением динамики является Второй Закон Ньютона. Согласно этому закону, ускорение, получаемое телом, равно отношению силы, действующей на тело, к массе тела:

Данный закон имеет векторную форму. То есть, ускорение, получаемое телом, имеет направление, и из уравнения следует, что это направление совпадает с направлением действия силы (поскольку масса – это скалярная величина).

Рис. 1. Второй закон Ньютона.

Видео:Физика. 10 класс. Основное уравнение динамики вращательного движения /08.10.2020/Скачать

Моменты силы и инерции

Общий принцип основного уравнения динамики для вращательного движения сохраняется. То есть, изменение скорости движения (ускорение) прямо пропорционально интенсивности воздействия, и обратно пропорционально инертности тела.

Но, особенность вращательного движения состоит в том, что одна и та же сила может сообщать точке различные угловые ускорения, в зависимости от точки ее приложения.

Это легко наблюдать на примере действия рычага, когда поднимается тяжелый предмет. Чем длиннее плечо приложения силы рычага, тем меньше требуется сила для подъема предмета, хотя масса предмета остается неизменной.

Рис. 2. Рычаг первого рода.

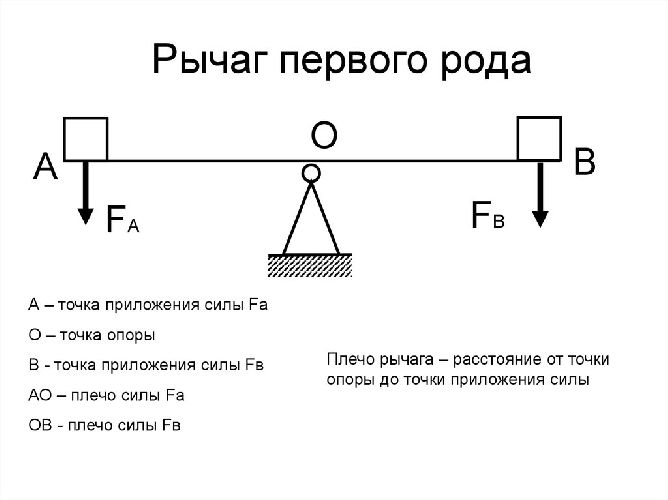
Таким образом, для вращательного движения обязательно необходимо учитывать плечо – расстояние от точки приложения силы до оси вращения. Для такого учета в уравнении сила и масса заменяется моментом силы и моментом инерции соответственно. Момент силы $M$ равен произведению модуля силы $F$ на плечо силы $l_F$ (расстояние от точки приложения до оси вращения). Момент инерции $J$ равен произведению массы материальной точки $m$ на квадрат расстояния от нее до оси вращения $l_F$.

Видео:Момент импульса. 10 класс.Скачать

Второй Закон Ньютона для вращения

Заменяя силу и массу во Втором Законе Ньютона на моменты силы и инерции, необходимо помнить, что ускорение, получаемое в такой формуле получается не линейным, а угловым $varepsilon$. Оно равно изменению угловой скорости $omega$ за единицу времени и измеряется в радианах в секунду за секунду. Скорость $omega$, приобретаемая телом в результате этого ускорения, также является угловой и измеряется в радианах в секунду:

• $varepsilon$ – угловое ускорение, получаемое телом;
• $М$ – момент силы, приложенной к телу;
• $J$ – момент инерции тела;
• $F$ – величина силы, приложенной к телу;
• $l_F$ – плечо силы, приложенной к телу;
• $m$ – масса тела;
• $l_m$ – расстояние от оси вращения до центра масс тела.

Отметим, что в данной формуле момент инерции рассчитывается для материальной точки, то есть, для случая, когда ось вращения лежит вне тела, а размерами тела можно пренебречь по сравнению с величиной плеча. Если ось вращения проходит через само тело или размеры тела сравнимы с величиной плеча, расчет момента инерции гораздо более сложен.

Видео:Семинар 3. Момент силы. Основное уравнение динамики вращательного движения.Скачать

Что мы узнали?

Уравнение динамики вращательного движения похоже на уравнение динамики поступательного движения. Но вместо силы и массы здесь используются момент силы и момент инерции. А получаемое ускорение является угловым, и измеряется в радианах в секунду за секунду.

📸 Видео

Моменты силы, импульса, инерции. Динамика вращательного движенияСкачать

Момент импульса. Закон сохранения момента импульса. Физика 10 классСкачать

Урок 109. Момент импульса. Закон сохранения момента импульсаСкачать

Момент импульса и момент силы относительно точки и оси | Студенты, абитуриенты МФТИ | Вуз. физика #1Скачать

Урок 94. Вычисление моментов инерции телСкачать

Поступательное и вращательное движенияСкачать

Общее уравнение динамики. Задача 1Скачать

Вращательное движение. 10 класс.Скачать