Вывод о релаксации давления после физической нагрузки на основании уравнения бернулли

Видео:Закон БернуллиСкачать

Основы гидравлики

Видео:Закон БернуллиСкачать

Уравнение Бернулли — фундамент гидродинамики

Бернулли — вне всякого сомнения — имя, знакомое и специалистам, и обывателям, которые хоть немного интересуются науками. Этот человек оставил ослепительный след в истории познавания человечеством окружающего мира, как физик, механик, гидравлик и просто общепризнанный гений, Даниил Бернулли навсегда останется в памяти благодарных потомков за свои идеи и выводы, которые долгое время существования человечества были покрыты мраком неизведанного.
Открытия и законы, которыми Бернулли осветил путь к познанию истины, являются фундаментальными, и придали ощутимый импульс развитию многих естественных наук. К таковым относится и уравнение Бернулли в Гидравлике, которое он вывел почти три века назад. Данное уравнение является основополагающим законом этой сложной науки, объясняющим многие явления, описанные даже древними учеными, например, великим Архимедом.

Попробуем уяснить несложную суть закона Бернулли (чаще его называют уравнением Бернулли), описывающего поведение жидкости в той или иной ситуации.

Выделим в стационарно текущей идеальной жидкости трубку тока, которая ограничена сечениями S₁ и S₂ , (рис. 1) .
(Понятие идеальной жидкости абстрактно, как и понятие всего идеального. Идеальной считается жидкость, в которой нет сил внутреннего трения, т. е. трения между отдельными слоями и частицами подвижной жидкости).
Пусть в месте сечения S₁ скорость течения ν₁ , давление p₁ и высота, на которой это сечение расположено, h₁ . Аналогично, в месте сечения S₂ скорость течения ν₂ , давление p₂ и высота сечения h₂ .

За бесконечно малый отрезок времени Δt жидкость переместится от сечения S₁ к сечению S₁‘ , от S₂ к S₂‘ .

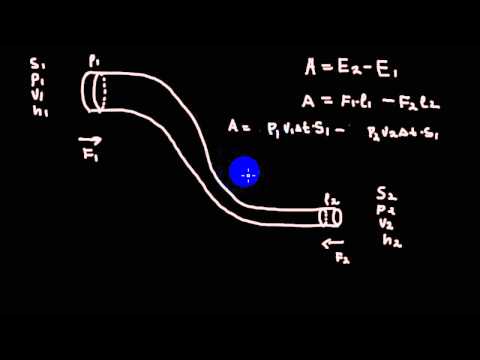
По закону сохранения энергии, изменение полной энергии E₂ — E₁ идеальной несжимаемой жидкости равно работе А внешних сил по перемещению массы m жидкости:

где E₁ и E₂ — полные энергии жидкости массой m в местах сечений S₁ и S₂ соответственно.

С другой стороны, А — это работа, которая совершается при перемещении всей жидкости, расположенной между сечениями S₁ и S₂ , за рассматриваемый малый отрезок времени Δt .
Чтобы перенести массу m от S₁ до S₁‘ жидкость должна переместиться на расстояние L₁ = ν₁Δt и от S₂ до S₂‘ — на расстояние L₂ = ν₂Δt . Отметим, что L₁ и L₂ настолько малы, что всем точкам объемов, закрашенных на рис. 1 , приписывают постоянные значения скорости ν , давления р и высоты h .
Следовательно,

где F₁ = p₁S₁ и F₂ = — p₂S₂ (сила отрицательна, так как направлена в сторону, противоположную течению жидкости; см. рис. 1).

Полные энергии E₁ и E₂ будут складываться из кинетической и потенциальной энергий массы m жидкости:

Подставляя (3) и (4) в (1) и приравнивая (1) и (2) , получим

Согласно уравнению неразрывности для несжимаемой жидкости, объем, занимаемый жидкостью, всегда остается постоянным, т. е.

Разделив выражение (5) на ΔV , получим

где ρ — плотность жидкости.

После некоторых преобразований эту формулу можно представить в другом виде:

Поскольку сечения выбирались произвольно, то в общем случае можно записать:

ρv 2 /2 +ρgh +p = const (6) .

Выражение (6) получено швейцарским физиком Д. Бернулли (опубликовано в 1738 г.) и называется уравнением Бернулли.

Даниил Бернулли (Daniel Bernoulli, 1700 — 1782), швейцарский физик, механик и математик, один из создателей кинетической теории газов, гидродинамики и математической физики. Академик и иностранный почётный член (1733) Петербургской академии наук, член Академий: Болонской (1724), Берлинской (1747), Парижской (1748), Лондонского королевского общества (1750).

Уравнение Бернулли по своей сути является интерпретацией закона сохранения энергии применительно к установившемуся течению идеальной жидкости. Уравнение хорошо выполняется и для реальных жидкостей, для которых внутреннее трение не очень велико.

Величина р в формуле (6) называется статическим давлением (давление жидкости на поверхность обтекаемого ею тела) , величина ρν 2 /2 — динамическим давлением, величина ρgh — гидростатическим давлением.

Статическое давление обусловлено взаимодействием поверхности жидкости с внешней средой и является составляющей внутренней энергии рассматриваемого элементарного объема жидкости (т. е. характеризуется взаимодействием внутренних частиц жидкости, вызванных внешним возмущением — давлением) , а гидростатическое – положением этого объема жидкости в пространстве (зависит от высоты над поверхностью Земли) .
Динамическое давление характеризует кинематическую составляющую энергии этого объема, поскольку зависит от скорости потока, в котором движется рассматриваемый элементарный объем жидкости.

Для горизонтальной трубки тока изменение потенциальной составляющей ρgh будет равно нулю (поскольку h2 – h1 = 0) , и выражение (6) примет упрощенный вид:

ρv 2 /2 + p = const (7) .

Выражение p + ρν 2 /2 называется полным давлением.

Таким образом, содержание уравнения Бернулли для элементарной струйки при установившемся движении можно сформулировать так: удельная механическая энергия при установившемся движении элементарной струйки идеальной жидкости, представляющая собой сумму удельной потенциальной энергии положения и давления и удельной кинетической энергии, есть величина постоянная.

Все члены уравнения Бернулли измеряются в линейных единицах.

В гидравлике широко применяют термин напор, под которым подразумевают механическую энергию жидкости, отнесенную к единице ее веса (удельную энергию потока или неподвижной жидкости) .
Величину v 2 /2g называют скоростным (кинетическим) напором, показывающим, на какую высоту может подняться движущаяся жидкость за счет ее кинетической энергии.
Величину h_п = p/ρg называют пьезометрическим напором, показывающим на какую высоту поднимается жидкость в пьезометре под действием оказываемого на нее давления.
Величину z называют геометрическим напором, характеризующим положение центра тяжести соответствующего сечения движущейся струйки над условно выбранной плоскостью сравнения.

Сумму геометрического и пьезометрического напоров называют потенциальным напором, а сумму потенциального и скоростного напора — полным напором.

На основании анализа уравнения Бернулли можно сделать вывод, что при прочих неизменных параметрах потока (жидкости или газа) величина давления в его сечениях обратно пропорциональна скорости, т. е. чем выше давление, тем меньше скорость, и наоборот.
Это явление используется во многих технических конструкциях и устройствах, например, в карбюраторе автомобильного двигателя (диффузор), в форме крыла самолета. Увеличение скорости воздушного потока в диффузоре карбюратора приводит к созданию разрежения, всасывающего бензин из поплавковой камеры, а специальная форма сечения самолетного крыла позволяет создавать на его нижней стороне зону повышенного давления, способствующего появлению подъемной силы.

Геометрическая интерпретация уравнения Бернулли

Поскольку напор измеряется в линейных величинах, можно дать графическую (геометрическую) интерпретацию уравнению Бернулли и его составляющим.

На графике (рис. 2) представлена горизонтальная плоскость сравнения 0-0 , относительно которой геометрический напор будет в каждом сечении равен вертикальной координате z центра тяжести сечения (линия геометрического напора проходит по оси струйки) .
Линия К-К , характеризующая потенциальный напор струйки, получена сложением геометрического и пьезометрического напора в соответствующих сечениях (т. е. разница координат точек линии К-К и соответствующих точек оси струйки характеризует пьезометрический напор в данном сечении) .
Полный напор характеризуется линией MN , которая параллельна плоскости сравнения О-О , свидетельствуя о постоянстве полного напора H’_e (удельной механической энергии) идеальной струйки в любом ее сечении.

При движении реальной жидкости, обладающей вязкостью, возникают силы трения между ограничивающими поток поверхностями и между слоями внутри самой жидкости. Для преодоления этих сил трения расходуется энергия, которая превращается в теплоту и рассеивается в дальнейшем движущейся жидкостью. По этой причине графическое изображение уравнения Бернулли для идеальной жидкости будет отличаться от аналогичного графика для реальной жидкости.
Если обозначить h_f потери напора (удельной энергии) струйки на участке длиной L , то уравнение Бернулли для реальной жидкости примет вид:

Для реальной жидкости полный напор вдоль струйки не постоянен, а убывает по направлению течения жидкости, т. е. его графическая интерпретация имеет вид не прямой линии, а некоторой кривой МЕ (рис. 3) . Заштрихованная область характеризует потери напора.

Падение напора на единице длины элементарной струйки, измеренной вдоль оси струйки, называют гидравлическим уклоном:

Гидравлический уклон положителен, если напорная линия снижается по течению жидкости, что всегда бывает при установившемся движении.

Для практического применения уравнения Бернулли необходимо распространить его на поток реальной жидкости:

где α₁ , α₂ — коэффициенты Кориолиса, учитывающие различие скоростей в разных точках сечения потока реальной жидкости.
На практике обычно принимают α₁ = α₂ = α : для ламинарного режима течения жидкости в круглых трубах α = 2, для турбулентного режима α = 1,04. 1,1.

Из уравнения Бернулли для горизонтальной трубки тока и уравнения неразрывности ( S₁v₁Δt = S₂v₂Δt ) видно, что при течении жидкости по горизонтальной трубе, которая имеет различные сечения, скорость жидкости больше в более узких местах (где площадь сечения S меньше) , а статическое давление больше в более широких местах, т. е. там, где скорость меньше. Это можно увидеть, установив вдоль трубы ряд манометров.

Данный опыт показывает, что в манометрической трубке В , которая прикреплена к узкой части трубы, уровень жидкости ниже, чем в манометрических трубках А и С , которые прикреплены к широкой части трубы, что соответствует уравнению Бернулли.

Так как динамическое давление зависит от скорости движения жидкости (газа) , то уравнение Бернулли можно использовать для измерения скорости потока жидкости. Принципиально это свойство жидкости для определения скорости потока реализовано в так называемой трубке Пито – Прандтля (обычно ее называют трубкой Пито ) .

Трубка Пито – Прандтля ( см. рис. 2 ) состоит из двух тонких стеклянных трубок, одна из которых изогнута под прямым углом (Г-образно) , а вторая — прямая.
Одним из свободных концов каждая трубка присоединена к манометру.
Изогнутая трубка имеет открытый свободный конец, направленный против тока и принимающий напор потока жидкости, а вторая погружена в поток перпендикулярно току, и скорость потока на давление внутри трубки не влияет, т. е. внутри этой трубки действует лишь статическая составляющая давления жидкости.
Разница между давлением в первой трубке (полное давление) и второй трубке (статическое давление) , которую показывает манометр, является динамическим давлением, определяемым по формуле:

Определив с помощью трубки Пито — Прандтля динамическое давление в потоке жидкости, можно легко вычислить скорость этого потока:

Уравнение Бернулли также используют для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Рассмотрим цилиндрический сосуд с жидкостью, с маленьким отверстием в боковой стенке на некоторой глубине ниже уровня жидкости.

Рассмотрим два сечения (на уровне h₁ свободной поверхности жидкости в сосуде и на уровне h₁ выхода ее из отверстия) и применим уравнение Бернулли:

Так как давления р₁ и р₂ в жидкости на уровнях первого и второго сечений равны атмосферному, т. е. р₁ = р₂ , то уравнение будет иметь вид

Из уравнения неразрывности мы знаем, что ν₁/ν₂ = S₂/S₁ , где S₁ и S₂ — площади поперечных сечений сосуда и отверстия.
Если S₁ значительно превышает S₂ , то слагаемым ν₁ 2 /2 можно пренебречь и тогда:

Это выражение получило название формулы Торричелли.
Формулу Торричелли можно использовать для подсчета объемного (или массового) расхода жидкости, истекающего из отверстия в сосуде с поддерживаемым постоянно уровнем под действием атмосферного давления.
При этом используется формула Q = vS (для определения массового расхода – m = ρvS ) , по которой определяется расход жидкости за единицу времени.

Если требуется узнать расход жидкости за определенный промежуток времени t , то его определяют, умножив расход за единицу времени на время t .

Следует отметить, что такая методика расчета расхода реальной жидкости через отверстие в стенке сосуда дает некоторые погрешности, обусловленные физическими свойствами реальных жидкостей, поэтому требует применения поправочных коэффициентов (коэффициентов расхода) .

Пример решения задачи на определение расхода жидкости

Определить примерный объемный расход воды, истекающей из отверстия диаметром 10 мм, проделанном в вертикальной стенке широкого сосуда на высоте h = 1 м от верхнего, постоянно поддерживаемого, уровня воды за 10 секунд.
Ускорение свободного падения принять равным g = 10 м/с 2 .
Коэффициент расхода воды через отверстие — µ_s = 0,62.

По формуле Торричелли определим скорость истечения воды из отверстия:

v = √2gh = √2×10×1 ≈ 4,5 м/с.

Определим расход воды Q за время t = 10 секунд:

Q = µ_svSt = 0,62×4,5×3,14×0,012/4 × 10 ≈ 0,0022 м 3 ≈ 2,2 литра.

На практике расход жидкости в трубопроводах измеряют расходомерами, например, расходомером Вентури. Расходомер Вентури (см рис. 2) представляет собой конструкцию из двух конических патрубков, соединенных цилиндрическим патрубком. В сечениях основной трубы и цилиндрического патрубка устанавливают трубки-пьезометры, которые фиксируют уровень жидкости, обусловленный полным давлением в потоке.

При прохождении жидкости через сужающийся конический патрубок часть потенциальной энергии потока преобразуется в кинетическую, и, наоборот, – при прохождении потока по расширяющемуся коническому патрубку, кинетическая энергия уменьшается, а потенциальная растет. Это сказывается на скорости движения жидкости по рассматриваемым участкам. Перепад высоты уровня жидкости в пьезометрах позволяет рассчитать среднюю скорость потока жидкости на рассматриваемых участках и вычислить объемный расход по внутреннему сечению трубы.
В расходомерах учитываются потери напора в самом приборе при помощи коэффициента расхода прибора φ .

Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Уравнение Бернулли и его применение

Разделы: Физика

Цели урока:

• Образовательные: знакомство с принципом Бернулли и его применением в технике и быту;
• Развивающие: развитие навыков проблемного подхода к решению поставленной задачи; развитие логического мышления учащихся; совершенствование умения наблюдать, сравнивать и сопоставлять изучаемые явления, выделять общие признаки и обобщать результаты экспериментов.
• Воспитательные: формирование научного мировоззрения, воспитание интереса и любознательности.

Оборудование: мультимедийный проектор, компьютер, интерактивная доска.

Демонстрационное оборудование: цилиндр Магнуса, по два бумажных листка на каждой парте учащихся, шарики для тенниса, фен, свеча и воронка, компьютерная модель (диск «Открытая физика 1.1»), рисунки.

1. Постановка учебной проблемы (просмотр видеосюжета, слайд 3).

Осенью 1912 г океанский пароход «Олимпик» плыл в открытом море, а почти параллельно ему, на расстоянии сотни метров, проходил с большой скоростью другой корабль, гораздо меньший, броненосный крейсер «Гаук». Когда оба судна заняли положение, изображенное на рисунке , произошло нечто неожиданное: меньшее судно стремительно свернуло с пути, словно повинуясь неведомой силе, повернулось носом к большому кораблю и, не слушаясь руля, двинулось почти прямо на него. «Гаук» врезался носом в бок «Олимпика».Удар был так силен, что «Гаук» проделал в борту «Олимпика» большую пробоину. Случай столкновения двух кораблей рассматривался в морском суде. Капитана корабля «Олимпик» обвинили в том, что он не дал команду пропустить броненосец. Как вы думаете, что произошло? Почему меньший корабль, не слушаясь руля, пошел наперерез «Олимпику»? Смоделируем это явление с помощью двух полосок бумаги.

Опыт 1. Между двумя полосками бумаги продуваем воздух, они сближаются. Скорость воздуха внутри полосок больше, значит давление между листами меньше, чем снаружи.

Парадоксальность результатов такого поведения тел можно объяснить, используя закон Берннули (уравнение Бернулли). Швейцарский ученый Даниил Бернулли длительное время жил в России, именно к этому времени относится создание его главного научного труда — теории гидромеханики. Основная теорема гидродинамики связывает давление жидкости с её скоростью. До сих пор вы рассматривали движение твердых тел. Сегодня мы перенесем знания законов сохранения на движение жидкостей и газов. Будем рассматривать закон Бернулли на качественном уровне.

2. Изучение нового материала.

Пусть жидкость течет без трения по трубе переменного сечения . Иначе говоря, через все сечения трубы проходят одинаковые объемы жидкости, иначе жидкости пришлось бы либо разорваться где-нибудь, либо сжаться, что невозможно. За время t через сечение S₁ пройдет объем

Делаем вывод: скорость течения жидкости в трубе переменного сечения обратно пропорциональна площади поперечного сечения.

Если площадь поперечного сечения увеличилась в 4 раза, то скорость уменьшилась во столько же раз и, наоборот, во сколько раз уменьшилось сечение трубы, во столько же раз увеличилась скорость течения жидкости или газа. Где наблюдается такое явление изменения скорости? Например, на реке, впадающей в море, наблюдается уменьшение скорости, вода из ванны — скорость увеличивается, мы наблюдаем турбулентное течение воды. Если скорость невелика, то жидкость течет как бы разделенная на слои («ламиниа» — слой). Течение называется ламинарным.

Итак, выяснили, что при течении жидкости из узкой части в широкую или наоборот, скорость изменяется, следовательно, жидкость движется с ускорением. А что является причиной возникновения ускорения? (Сила (второй закон Ньютона)). Какая же сила сообщает жидкости ускорение? Этой силой может быть только разность сил давления жидкости в широкой и узкой частях трубы.

К этому выводу впервые пришел академик Петербургской академии наук Даниил Бернулли в 1726 году, и закон теперь носит его имя. Принцип, впервые высказанный Д.Бернулли в 1726 г., гласит: в струе воды или воздуха давление велико, если скорость мала, и давление мало, если скорость велика. Существуют известные ограничения этого принципа, но здесь мы не будем на них останавливаться.

Опыт 2. Работа с интерактивной моделью [5].

Уравнение Бернулли показывает, что давление жидкости (или газа) больше там, где скорость её течения меньше и наоборот. Этот, казалось бы, парадоксальный вывод подтверждается опытами .

Даниил Бернулли (29.1.1700- 17.3.1782), сын Иоганна Бернулли (брат — Якоб Бернулли) . Занимался физиологией и медициной, но больше всего математикой и механикой. В 1725-33 он работал в Петербургской АН сначала на кафедре физиологии, а затем механики. Впоследствии он состоял почётным членом Петербургской АН, опубликовал (с 1728-78) в её изданиях 47 работ. В работах, завершенных написанным в Петербурге трудом «Гидродинамика» (1738), вывел основное уравнение стационарного движения идеальной жидкости, носящее его имя. Даниил Бернулли разрабатывал кинетические представления о газах.После рассмотрения принципа Бернулли можно объяснить причины столкновения двух кораблей .

Объяснение поведения двух листочков при продувании воздуха между ними . Давление воздуха в пространстве левее и правее листочков бумаги равно атмосферному давлению.Направив воздушный поток между листочками, мы тем самим в этом скоростном потоке воздуха создаем область пониженного давления в соответствии с законом Бернулли, в результате чего возникает разность давлений в пространстве между листками и с внешней стороны листков. Эта разность давлений является причиной «прилипания» листочков.

Опыт 3. Взять листок бумаги за короткую сторону и подуть вдоль листа. Лист поднимается вверх. Объяснение опыта: Скорость над листом больше, чем под листом, а давление меньше. Эта разность давлений и поднимает лист вверх .

Аэродинамический принцип создания подъемной силы был изложен Н. Е. Жуковским так: «. двигаясь под малым углом к горизонту с большой горизонтальной скоростью, наклонная плоскость сообщает громадному количеству последовательно прилегающего к ней воздуха малую скорость вниз и тем развивает большую подъемную силу вверх при незначительной затрате работы на горизонтальное перемещение». Следовательно, для создания подъемной силы по этому принципу необходимо перемещение тела относительно воздуха.
Аэродинамический принцип создания подъемной силы используется при подъеме аппарата тяжелее воздуха, к которым относятся планеры и дельтапланы, самолеты и сверхлегкие моторные летательные аппараты, вертолеты и автожиры, летательные аппараты с машущими крыльями (ортоптеры и орнитоптеры).

Подъемная сила у моторного сверхлегкого летательного аппарата создается неподвижно закрепленным крылом. При поступательном движении аппарата крыло обтекается потоком воздуха. Из-за особой формы сечения крыла (несимметричная форма) воздух, огибающий крыло сверху, движется быстрее, чем внизу, поэтому создается разность давлений под крылом и над ним, а в результате возникает подъемная сила. Для моторного аппарата перемещение в воздухе происходит под действием силы тяги, создаваемой силовой установкой.
Планеры, в том числе дельтапланы, создают подъемную силу так же, как моторные аппараты, неподвижно закрепленным крылом, но так как они не имеют силовой установки, то могут только планировать или летать на буксире. При планировании они снижаются за счет силы веса или набирают высоту за счет восходящих потоков воздуха. Подъемная сила появляется при обтекании не всех тел, а лишь тел с определенным профилем. Для крыльев дельтапланов должны применяться профили с хорошими летными характеристиками, создающими большую подъемную силу.

Жуковский Николай Егорович (5.I.1847-17.III.1921). Русский ученый в области механики, основоположник современной гидроаэродинамики. Жуковский является автором многочисленных оригинальных исследований в области механики твердого тела, астрономии, математики, гидродинамики и гидравлики, прикладной механики, теории регулирования машин и др.

Работы Жуковского в области аэродинамики явились источником основных идей, на которых строится авиационная наука. Он всесторонне исследовал динамику полёта птиц, теоретически предсказал ряд возможных траекторий полёта. В 1904 году Жуковский открыл закон, определяющий подъёмную силу крыла самолёта; определил основные профили крыльев и лопастей винта самолёта; разработал вихревую теорию воздушного винта. При его активном участии были созданы Центральный аэродинамический институт (ЦАГИ), Военно-воздушная инженерная академия (ныне носит имя Жуковского).

Проблема изучения подъемной силы имеет очень давнюю историю. Загадки полета птицы занимали умы ученых задолго до появления летательных аппаратов. Первая попытка исследования природы подъемной силы была сделана Леонардо да Винчи в 1505 году. Объясняя причину возникновения подъемной силы птицы, он считал, что из-за быстрых ударов крыльями воздух под ними уплотняется и поэтому поддерживает птицу. Эта гипотеза Леонардо да Винчи, основанная на сжимаемости воздуха, была ошибочной, так как применялась для полета с малыми скоростями, когда свойство сжимаемости воздуха практически не проявляется.

В 1852 году Магнус провел серию опытов для объяснения явления отклонения от вертикальной плоскости вращающихся артиллерийских снарядов. Он показал, что поперечная сила, вызывающая это отклонение, возникает из-за взаимодействия двух потоков воздуха: набегающего на снаряд и вращающегося вместе со снарядом. Это явление, получившее название эффекта Магнуса.

Опыт 4. Для опыта изготовим цилиндр из плотной, но не толстой бумаги диаметром 5 см, длиной 25-30 см. На цилиндр намотаем ленточку, один конец которой прикрепим к линейке. Резким движением вдоль горизонтальной поверхности стола сообщим цилиндру сложное движение (поступательное и вращательное) . При большой скорости цилиндр поднимается вверх и описывает небольшую вертикальную петлю. Объясните, почему это происходит.

Уравнение Бернулли объясняет такое поведение рулона (и закрученного мячика): вращение нарушает симметричность обтекания за счёт эффекта прилипания. С одной стороны бумажного цилиндра скорость потока больше (над цилиндром вектор скорости воздуха сонаправлен вектору скорости цилиндра), значит, давление там понижается, а под цилиндром вектор скорости воздуха антипараллелен вектору скорости цилиндра. В результате разности давлений возникает подъёмная сила, называемая силой Магнуса. Эта сила поднимает цилиндр вверх, а не по параболе.

Это явление носит название эффекта Магнуса, по имени ученого, открывшего и исследовавшего его экспериментально. Эффект Магнуса проявляется в таких природных явлениях, как образование смерчей над поверхностью океана. В месте встречи двух воздушных масс с разными температурами и скоростями возникает вращающийся вокруг вертикальной оси столб воздуха и несется вперед. В поперечнике такой столб может достигать сотен метров и несется со скоростью около 100м/с. Из-за быстрого вращения воздух отбрасывается к периферии вихря и давление внутри него понижается. Когда такой столб приближается к воде, то засасывает ее в себя, представляя огромную опасность для судов.

3. Закрепление нового материала.

По рисункам и демонстрациям объясните наблюдаемые явления (Слайд 12).

Опыт 5. «Демон» Бернулли.

Струя воздуха может поддерживать легкий шарик (например мяч для настольного тенниса). Воздушная струя ударяется о шарик и не дает ему падать. Когда шарик выскакивает из струи, окружающий воздух возвращает его обратно в струю, т.к. давление окружающего воздуха, имеющего малую скорость, велико, а давление воздуха в струе, имеющего большую скорость, мало. Дополнительная подъемная сила может возникать из-за вращения мяча вследствие эффекта Магнуса, который проявляется и при полете закрученного бейсбольного мяча. (Нередко подъемную силу, возникающую в рассматриваемом случае, ошибочно объясняют уменьшением давления в воздушной струе вследствие движения воздуха. Это неправильное истолкование смысла уравнения Бернулли. На самом деле давление в свободно движущейся воздушной струе равно атмосферному. Если насадка на шланг пылесоса сужается (как это обычно бывает), то скорость воздушного потока увеличивается, а давление уменьшается. Таким оно остается и в струе, пока в нее не будет «затянут» окружающий воздух. Тогда давление станет равным атмосферному. Поперечная устойчивость мяча объясняется уменьшением давления в струе, обтекающей мяч.)

Опыт 6. Воздух продувается между двумя воздушными шариками, подвешенными на нитях. Шарики сближаются и ударяются друг о друга.

Опыт 7. Напротив воронки зажигаем свечу. Через воронку продуваем воздух, пламя свечи отклоняется в сторону воронки.

Обсуждение рисунков (Слайд 14).

Ситуация 1. Ветер под зданием. В США был предложен проект жилого дома, в котором этажи, подобно мостам, «подвешиваются» между двумя мощными стенами, а пространство под домом остается открытым . Внешне такое здание выглядит весьма привлекательно, но оно абсолютно не пригодно для ветреных районов. Одно из таких зданий было выстроено на территории Массачусетского технологического института. И вот когда подули весенние ветры, скорость ветра под зданием достигла 160 км/ч. Чем вызвано столь сильное увеличение скорости ветра? (Ветер, попадающий на здание, частично прогоняется через нижний просвет. При этом скорость его возрастает).

Ситуация 2. Встречные поезда. Скоростные поезда . при встрече должны замедлить ход, иначе стекла в вагонах разобьются. Почему? В какую сторону при этом выпадают стекла: внутрь вагонов или наружу? Может ли случиться подобное, если поезда движутся в одном направлении? Будет ли вас притягивать к поезду или отталкивать от него, если вы окажетесь слишком близко от быстро идущего поезда?

(Впереди быстро идущего поезда создается фронт высокого давления, а за ним — область низкого давления. Когда встречные поезда разъезжаются, стекла в вагонах могут быть выдавлены наружу, поскольку между поездами возникает область пониженного давления).

Ситуация 3. Крылья и вентиляторы на гоночных автомобилях. Гоночные автомобили за время своего существования претерпели существенные изменения. К числу наиболее значительных усовершенствований можно отнести установку в задней части автомобиля горизонтального крыла. Когда автомобиль с таким крылом совершал поворот, водитель наклонял крыло вперед. При выходе из поворота, крыло снова принимало горизонтальное положение. Это устройство оказалось очень эффективным средством удержания машины на дороге во время поворотов и позволяло делать повороты с гораздо большей скоростью. Однако поломка таких крыльев на трассе делала машину неуправляемой, и поэтому пришлось установить неподвижные крылья. Каким образом крылья — подвижные или неподвижные — могут удерживать автомобиль на повороте?

Одна из самых странных гоночных машин «Чаппараль-2.1» была построена Джимом Холлом, который придумал и подвижное крыло. Почти 20 лет прошло с момента первых экспериментов легендарного Джима Холла с «машиной-крылом» Chapparal-Chevrolet до победы в Гран При «гоночного пылесоса», целиком и полностью обязанного своим преимуществом «граунд-эффекту». «Чаппараль» имел в задней части два больших вентилятора, которые засасывали воздух из-под днища и гнали его назад. Сбоку автомобиль был закрыт щитками почти до самой дороги, чтобы воздух проходил прямо под машиной. Благодаря этому Холлу удалось увеличить сцепление колес с дорогой и тем самым значительно повысить скорость автомобиля. Почему воздух, прогоняемый под машиной и выпускаемый позади, усиливает сцепление колес с дорогой? Можете ли вы оценить увеличение сцепления и скорости?

(Наклоненное вниз крыло создавало силу, направленную вниз; тем самым улучшалось сцепление колес с дорогой. Это позволяло машине быстрее проходить повороты. Аэродинамическая сила крыла здесь создавалась так же, как и на самолете, только в данном случае она была направлена вниз. Вентилятор в задней части автомобиля тоже создавал направленную вниз силу, увеличивающую сцепление колес с дорогой. Воздух, который засасывался под автомобиль, ускорялся, так как сечение воздушного потока уменьшалось. Согласно уравнению Бернулли, увеличение скорости потока сопровождается понижением давления. Таким образом, давление над автомобилем оказывалось выше, чем под ним, и автомобиль почти в полтора раза сильнее прижимался к дороге).

Ситуация 4. «Ветроход». Всегда находятся люди, способные увидеть то, чего не замечают другие, и обладающие неиссякаемой пытливостью — этим неотъемлемым качеством всех изобретателей. Таким человеком был немецкий инженер Антон Флеттнер (1885-1961). Однажды, наблюдая во время плавания на паруснике за усилиями матросов, работавших в шторм с парусами на высоте 40-50 м, он подумал: а нельзя ли чем-нибудь заменить классический парус, используя при этом все ту же силу ветра? Размышления заставили Флеттнера вспомнить о его соотечественнике физике Генрихе Густаве Магнусе. В качестве первого опытного судна для его испытания использовали видавшую виды трехмачтовую шхуну «Букау» водоизмещением 980 т. В 1924 году на ней вместо трех мачт поставили два ротора-цилиндра высотой 13,1 м и диаметром 1,5 м. Их приводили в движение два электромотора постоянного тока напряжением 220 В. Объясните принцип действия такого «ветрохода» . (Если на поверхность вращающегося ротора воздействует ветер, скорость последнего изменяется. Там, где поверхность движется навстречу ветру, его скорость уменьшается, а давление увеличивается. С противоположной же стороны ротора скорость воздушного потока, наоборот, увеличивается, а давление падает. Полученная разность давлений и создает движущую силу, которую можно использовать для перемещения судна).

Магнус в 1852 г доказал, возникающая поперечная сила, действующая на тело, вращающееся в обтекающем его потоке жидкости или газа, направлена в сторону, где скорость потока и вращение тела совпадают. Наличие такого эффекта Магнус подтвердил позже на опыте с весами. На одну из их чаш клали горизонтально цилиндр с подключенным к нему моторчиком, а на другую — уравновешивавшие гири. Цилиндр обдували воздухом, но, пока не включали моторчик, он оставался неподвижным, и равновесие весов не нарушалось. Однако стоило лишь запустить моторчик и тем самым заставить цилиндр вращаться, как чаша, где он находился, или поднималась, или опускалась — в зависимости от того, в каком направлении шло вращение. Этим опытом ученый установил: если на вращаемый цилиндр набегает поток воздуха, то скорости потока и вращения по одну сторону цилиндра складываются, по другую же — вычитаются. А поскольку большим скоростям соответствуют меньшие давления, на вращаемом цилиндре, помещенном в поток воздуха, возникает движущая сила, перпендикулярная потоку. Ее можно увеличивать или уменьшать, если крутить цилиндр быстрее или медленнее. Именно опыты Магнуса и навели Флеттнера на мысль заменить парус на судне вращающимся цилиндром. Но сразу же возникли сомнения. Ведь на большом судне такие роторы будут выглядеть огромными башнями высотой 20-25 м, которые в шторм создадут колоссальную опасность для судна. На эти вопросы требовалось ответить, и Флеттнер начал свои исследования, которые завершились созданием первого «ветрохода» — трехмачтовая шхуна «Букау».

Ситуация 5. В дождливую ветряную погоду, каждый из нас замечал, что раскрытые зонтики иногда «выворачиваются наизнанку» . Почему это происходит? Аналогичное действие производит на крыши домов сильный ураган. (Поток воздуха, набегающий на изогнутую поверхность зонта, движется по руслу своеобразной сужающейся трубы с большей скоростью, чем воздух в нижней части, следовательно, давление снизу больше, чем вверху, и зонт выворачивается)

Ситуация 6. В футболе одним из коварных ударов для вратаря считается так называемый «сухой лист» . Похожий подрезанный удар — «сплин» применяют в теннисе и других играх с мячом. Предвидеть, куда направится такой крученый мяч, неопытному спортсмену довольно трудно. Объясните, почему так происходит. («Виновата» во всем сила Магнуса, проявляющаяся при движении закрученного вдоль своей оси симметричного тела — мяча, цилиндра и т.п.).

Уравнение Бернулли просто объясняет множество явлений, происходящих в жидкости и газе. Это возникновение подъемной силы крыла, работа таких приборов как пульверизатор, карбюратор, газовой горелки и многое другое. Жизнь самого Даниила Бернулли похожа на его замечательное уравнение. Движение по разным городам и странам, взаимодействие со многими учеными, периодическое расширение и сжатие научных интересов в конечном итоге привели к результатам, которыми до сих пор пользуется человечество, находя все новые и новые применения.

Рефлексия. Конструирование бумажного самолетика. Чей самолет имеет большую дальность полета?

Домашнее задание. Применение закона Бернулли и эффекта Магнуса (рисунки, кроссворды, презентации, стихи)

Видео:Уравнение Бернулли гидравликаСкачать

Уравнение Бернулли

Уравнение Бернулли для струйки жидкости формулируется следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т.е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии – есть величина постоянная во всех сечениях струйки.

Уравнение Бернулли выглядит так:

Подробное описание всех входящих в состав уравнения параметров уже описан в этой статье.

Содержание статьи

Видео:Влияние физических нагрузок на артериальное давление и частоту пульса у человекаСкачать

Смысл уравнения Бернулли

По существу вывода уравнение Бернулли для струйки идеальной жидкости представляет собой закон сохранения механической энергии, составленный применительно к единице массового расхода жидкости. Это следует из того, что в процессе вывода значения работы сил, приложенных к выделенному объему струйки и значения кинетической энергии этого объема были поделены на величину ρqΔT.

Отсюда вытекает, что поскольку член υ 2 /2 является мерой кинетической энергии единицы массы движущейся жидкости, то сумма членов gz+p/ρ будет мерилом ее потенциальной энергии.

В отношении величины gz это очевидно, ведь если частица жидкости массы m расположена на высоте z относительно некоторой плоскости и находится под действием сил тяжести, то способность ее совершить работу, т.е. её потенциальная энергия относительно этой плоскости равняется mgz. Но если её поделить на массу частиц m, то эта часть потенциальной энергии даст величину gz.

Для более ясного физического представления о том, что потенциальная энергия измеряется величиной p/ρ рассмотрим такую схему: пусть к трубе, заполненной жидкостью с избыточным давлением p, присоединен пьезометр, снабженный на входе в него краном.

Кран сначала закрыт, т.е. пьезометр свободен от жидкости, а элементарный объем жидкости ΔV массой ρ*ΔV перед краном находится под давлением p.

Если затем открыть кран, то жидкость в пьезометре поднимется на некоторую высоту, равную

Таким образом, единица массы, находящейся под давлением p, как бы несет в себе ещё заряд потенциальной энергии, определяемой величиной p/ρ.

В гидравлике для характеристики удельной энергии обычно используется понятие напор, под которым понимают энергию жидкости, отнесенную к единице силы тяжести, а не её массы. В соответствии с этим уравнение Бернулли записанное в начале этой статьи примет вид

Такое уравнение Бернулли для элементарной струйки идеальной жидкости в другой форме, весьма удобно для гидравлических расчетов и может быть сформулировано следующим образом.

Для элементарной струйки идеальной жидкости полный напор, т.е. сумма геометрического, пьезометрического и скоростного напоров, есть величина постоянная во всех её сечениях.

Отсюда следует, что между напором и удельной энергией существует очень простая зависимость

где э – удельная энергия

Уравнение Бернулли для элементарной струйки реальной жидкости

Если вместо идеальной жидкости рассматривать жидкость реальную, то уравнение Бернулли для реальной жидкости должно принять несколько другой вид.

При движении идеальной жидкости её полная удельная энергия или напор сохраняет постоянное значение по длине струйки, а при движении реальной жидкости эта энергия будет убывать по направлению движения. Причиной этого являются затраты энергии на преодоление сопротивлений движению, обусловленные внутренним трением в вязкой жидкости.

Если же мы рассмотрим два сечения для струйки идеальной жидкости: 1-1 в начале и 2-2 в конце струйки, то полная удельная энергия будет

Полная удельная энергия для сечения 1-1 всегда будет больше, чем полная удельная энергия для сечения 2-2 на некоторую величину потерь, и уравнение Бернулли в этом случае получается

Величина Э_1-2 представляет собой меру энергии, потерянную единицей массы жидкости на преодоление сопротивлений при её движениями между указанными сечениями.

Соответствующий этой потере удельной энергии напор называют потерей напора между сечениями 1-1 и 2-2 и обозначают h_1-2 . Поэтому уравнение Бернулли для элементарной струйки реальной жидкости можно представить в виде

Уравнение Бернулли для потока реальной жидкости

Уравнение Бернулли для струйки реальной жидкости это еще только половина дела, ведь в при решении различных практических вопросов о движении жидкостей приходится иметь дело с потоками конечных размеров. Уравнение Бернулли в этом случае может быть получено, исходя из рассмотрения потока как совокупности множества элементарных струек.

Учитывая, что все струйки движутся с одной и той же средней скоростью форма записи уравнения Бернулли для потока идеальной жидкости становится идентичной его записи для элементарной струйки.

В таком виде уравнение Бернулли обычно и применяется при решении практических задач для потоков однородной несжимаемой жидкости при установившемся движении, происходящем под действием одной силы тяжести.

Такое уравнение составляется для различных живых сечений потока, вблизи которых движение жидкости должно удовлетворять условиям медленно изменяющегося движения, хотя на пути между этими сечениями движение может и не удовлетворять указанным условиям.

Слагаемое h_1-2 в этом уравнении показывает потери напора на преодоление сопротивлений движению жидкости. При этом в гидравлике различают два основных вида сопротивлений:
— h_лп — линейные потери — сопротивления, проявляющиеся по всей длине потока, обусловленные силами трения частиц жидкости друг о друга и о стенки, ограничивающие поток.
— h_мп — местные потери – местные сопротивления, обусловленные различного рода препятствиями, устанавливаемыми в потоке (задвижка, кран, колено), приводящими к изменениям величины или направления скорости течения жидкости

Поэтому полная потеря напора между двумя сечениями потока при наличии сопротивлений обоих видов будет

Видео по теме

Уравнение Бернулли подходит и для газов. Явление уменьшения давления при повышении скорости потока является основой работы различных приборов для измерения расхода. Закон Бернулли справедлив и для жидкостей вязкость которых равна нулю. При описании течения таких жидкостей используют уравнение Бернулли с добавлением слагаемых учитывающих потери на местные сопротивления.

📽️ Видео

Уравнение БернуллиСкачать

Уравнение Бернулли. Практическая часть. 10 класс.Скачать

Артериальное давление при физической нагрузке После физической нагрузки повышается давлениеСкачать

Уравнение БернуллиСкачать

Эффект Вентури и трубка Пито (видео 16) | Жидкости | ФизикаСкачать

Основы гидродинамики и аэродинамики | уравнение БернуллиСкачать

Гидродинамика. Вывод уравнения БернуллиСкачать

Эффект Магнуса и уравнение БернуллиСкачать

Характеристика насосной системы. Потери по длине трубопровода.Скачать

Трубка Пито и скоростной напорСкачать

Урок 134. Применения уравнения Бернулли (ч.1)Скачать

Парадокс сужающейся трубыСкачать

Скорость восстановления после физической нагрузкиСкачать

Эффект МагнусаСкачать