В РИС все параметры по объему постоянны.
| Физическая модель РИВ-Н– длинная узкая труба, в которой все частицы движутся в заданном направлении, не перемешиваясь и вытесняя, подобно поршню, находящиеся впереди частицы потока и постепенно потоки вещества претерпевают превращение по высоте реактора. Время пребывания всех частиц в гаком реакторе постоянно: | 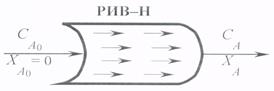 |
Все характеристики (концентрация СA, степень превращения ХА, температура Т и др.) изменяются плавно по объему реактора,поэтому материальный баланс для всего объема реактора составить нельзя.
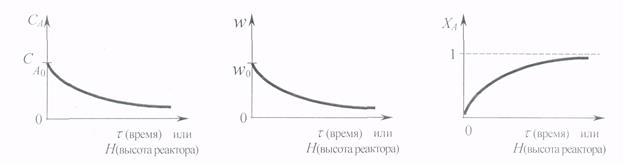
Рис.2. Графики зависимостей:
а) СА=f (τ или H) б) w= f (τ или H) в)ХА= f (τ или H)
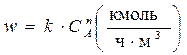
Выбирают бесконечно малый объем реактора dVи для него составляют материальный баланс. Затем проводят интегрирование этих бесконечно малых объемов по всему объему реактора.
Пусть простая необратимая реакция протекает в реакторе без изменения объема υ:
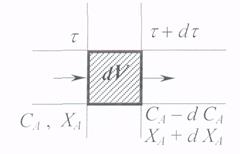 | реагент продукт А → R . CAпонижается, ХА увеличивается. Материальный баланс процесса: Gприх.=Gрасх., Gрасх.=Gулетевш.частиц +Gчастиц.прореагр., в ХР |
где 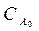
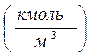
υ- объемный расход
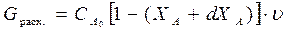
где V- объем реактора (м 3 );
dV- элементарный объем реактора (м 3 ).
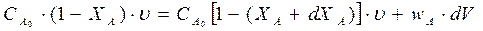
(Приход) 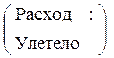
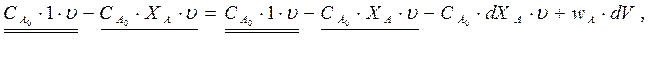
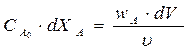
элементарного объема РИВ-Н
Для получения уравнения мат. баланса всего реактора полученное уравнение после разделения переменных проинтегрируем (по объему всего реактора):
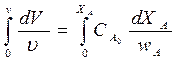
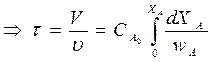
где wA находим, зная кинетику процесса.
Характеристическое уравнение РИВ-Н позволяет, зная кинетику процесса
(для нахождения wА), определить время τпребывания реагентов в реакторе доля достижения заданной степени превращения ХА, а затем — и размеры реактора.
Для реакции п -го порядка :
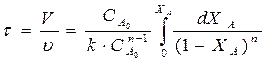
где п — порядок реакции.
— зависит только от степени превращения ХА и не зависит от начальной концентрации 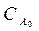
В некоторых производственных реакторах степень превращения ХА столь незначительна, что для расчета можно применить модель РИВ— это трубчатые контактные аппараты с катализатором в трубах или межтрубном пространстве («кожухотрубчатые»), служащие для гетерогенных газофазных реакций.
Модель вытеснения также применяется при проектировании жидкофазных трубчатых реакторов с большим отношением длины трубы к ее диаметру.
При одинаковых условиях проведения одной и той же реакции для достижения равной глубины превращения среднее время пребывания реагентов в проточном реакторе идеального смешения больше, чем в реакторе идеального вытеснения. В РИС концентрации во всех точках равны конечной концентрации, а в РИВ в 2-х соседних точках концентрации реагентов отличаются. Скорость реакции, согласно ЗДМ пропорциональна концентрации реагентов. Следовательно в РИВ она всегда выше, чем в РИС. Т.е. требуется меньшее время пребывания для достижения той же глубины превращения.
Дата добавления: 2016-06-02 ; просмотров: 4288 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Химические реакторыСкачать

Материальный баланс РИС-Н
Описание модели РИС-Н
Реактор идеального смешения непрерывного действия представляет собой ёмкостный аппарат с перемешивающим устройством. Реакционная смесь подается в аппарат и выгружается из него непрерывно.
Рисунок. Схема проточного реактора идеального смешения:
1 – геометрический объем реактора;
2 – реакционный объем;
3 – мешалка;
4 – штуцер для аварийного опорожнения реактора.
Vo – объемный расход реакционной смеси;
САо, ХАо – начальная концентрация и степень превращения реагента А;
СА, ХА – конечная концентрация и степень превращения реагента А;
Т.Н. – теплоноситель или хладагент.
В РИС-Н выполняются следующие допущения:
1. В результате интенсивного перемешивания все параметры в реакционном объёме полностью выравнены.
2. Изменение параметров входного потока при попадании в реакционный объём происходит мгновенно.
3. Параметры выходного потока равны параметрам внутри реакционного объёма.
Для реакторов непрерывного действия характерен стационарный режим работы, то есть параметры в реакторе не изменяются с течением времени. Неустановившееся состояние наблюдается только в пусковой период и в период остановки реактора.
В дальнейшем все реакторы непрерывного действия будут рассматриваться только в стационарном режиме, когда отсутствует накопление вещества и тепла.
Исходя из идеальности перемешивания, в качестве элементарного объема для реактора идеального смешения можно принять весь реакционный объем реактора Vр. По условию стационарности в качестве элементарного промежутка времени можно принять любой промежуток времени τ.
Изменение концентрации реагента А в реакторе идеального смешения непрерывного действия по реакционному объему аппарата и по времени
В реальных условиях приблизиться к режиму идеального смешения можно, применяя интенсивное перемешивание реакционной смеси. Наряду с этим, форма и размеры емкостного аппарата должны быть оптимальными для уменьшения объема застойных зон.
Материальный баланс РИС-Н
Материальный баланс показывает изменение количества реагента или продукта за счёт его поступления (со знаком плюс) и расходования (со знаком минус) в элементарном объёме за элементарный промежуток времени.
Запишем материальный баланс РИС-Н по взятому в недостатке реагенту A:
Здесь NAвх − количество (в молях) реагента A, поступающего со входящим в элементарный объём потоком реакционной массы за элементарный промежуток времени,
NAвых − количество (в молях) реагента A, уходящего с выходящим из элементарного объёма потоком реакционной массы за элементарный промежуток времени,
NAх.р − количество (в молях) реагента A, расходуемого на протекание химической реакции в элементарном объёме за элементарный промежуток времени.
Входящие в состав материального баланса РИС-Н слагаемые могут быть выражены через параметры процесса следующим образом:

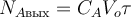
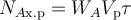
При подстановке полученных выражений в уравнение материального баланса РИС-Н получим:
Преобразуем выражение, сократив на элементарный промежуток времени τ, и вынеся за скобку объёмный расход смеси Vo:
Отношение реакционного объёма реактора Vр к объёмному расходу реакционной смеси Vo соответствует среднему времени пребывания частиц в проточном реакторе:
Выразив среднее время пребывания частиц в реакторе, получим характеристическое уравнение РИС-Н:
Учитывая, что 
Тепловой баланс РИС-Н
Тепловой баланс показывает изменение количества теплоты за счёт её поступления (со знаком плюс) и расходования (со знаком минус) в элементарном объёме за элементарный промежуток времени.
Запишем тепловой баланс политермического РИС-Н:
Здесь Qвх − количество теплоты, поступающей со входящим в элементарный объём потоком реакционной массы за элементарный промежуток времени,
Qвых − количество теплоты, уходящей с выходящим из элементарного объёма потоком реакционной массы за элементарный промежуток времени,
Qх.р − количество теплоты, выделяющейся (со знаком плюс) или поглощаемой (со знаком минус) при протекании химической реакции в элементарном объёме за элементарный промежуток времени,
Qт.о − количество теплоты, вносимой (со знаком плюс) в элементарный объём или отводимой (со знаком минус) из него за счёт теплообмена с теплоносителем или хладагентом за элементарный промежуток времени.
Входящие в состав теплового баланса РИС-Н слагаемые могут быть выражены через параметры процесса следующим образом:
(здесь ρo − плотность входящей в элементарный объём реакционной смеси, Vo − объёмный расход реакционной смеси, cpo − удельная теплоёмкость входящей в элементарный объём реакционной смеси, To − температура входящей в элементарный объём реакционной смеси, τ − элементарный промежуток времени),
(здесь ρ − плотность выходящей из элементарного объёма реакционной смеси, Vo − объёмный расход реакционной смеси, cp − удельная теплоёмкость выходящей из элементарного объёма реакционной смеси, T − температура выходящей из элементарного объёма реакционной смеси, τ − элементарный промежуток времени)
(здесь ΔH − тепловой эффект химической реакции, WA − скорость химической реакции по компоненту A, Vр − реакционный объём реактора, τ − элементарный промежуток времени)
(здесь Kт − коэффициент теплопередачи между теплоносителем или хладагентом и реакционной массой, F − поверхность теплообмена между теплоносителем или хладагентом и реакционной массой, ΔT − положительная разность температур между теплоносителем или хладагентом и реакционной массой, τ − элементарный промежуток времени).
При подстановке полученных выражений в уравнение теплового баланса РИС-Н получим:
Преобразуем выражение, сократив на элементарный промежуток времени τ, и предполагая, что плотность и теплоёмкость реакционной смеси слабо зависят от температуры (ρocpo ≈ ρcp):
Выразим из материального баланса РИС-Н скорость реакции WA:
Подставим это выражение в тепловой баланс и разделим все слагаемые на CAoVo:
Учитывая, что мольная теплоёмкость с ‘ p может быть рассчитана по формуле 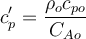
В случае адиабатического теплового режима, характеризующегося отсутствием теплообмена реакционной смеси с теплоносителем или хладагентом (тепловая изоляция реактора), тепловой баланс РИС-Н примет вид:
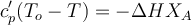
В случае изотермического теплового режима, характеризующегося постоянством температуры реакционной смеси, можно принять Qвх ≈ Qвых:
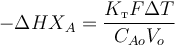
Видео:РеакторСкачать

Математические модели процессов в идеальных реакторах
Читайте также:
|

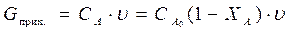
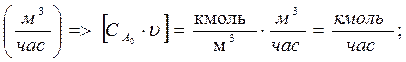
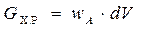
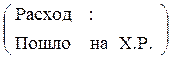
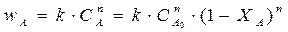
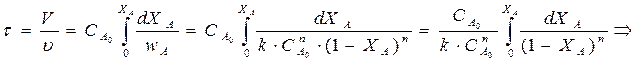
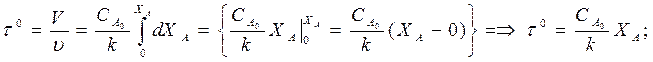
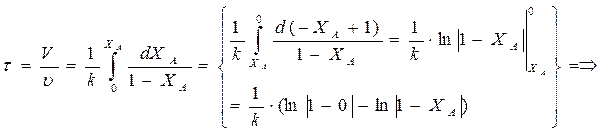
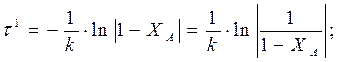
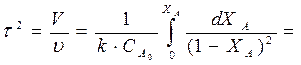
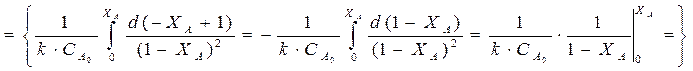
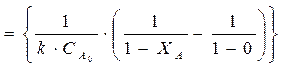
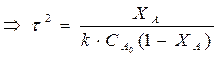

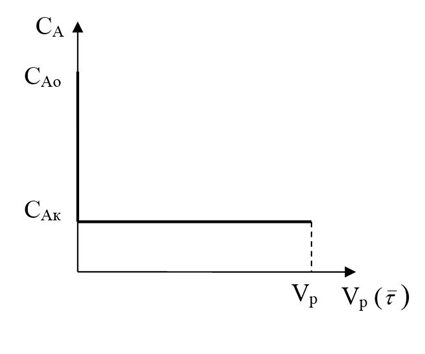
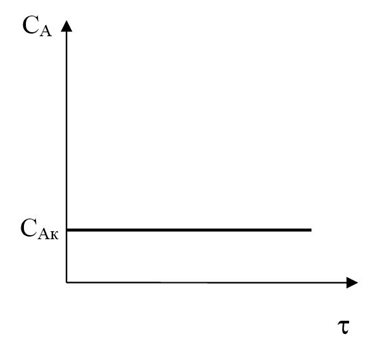
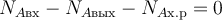
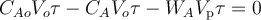

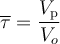
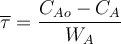
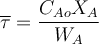
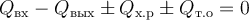
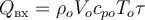
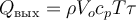
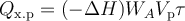

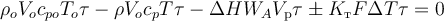
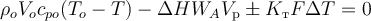


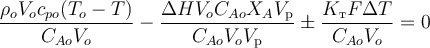
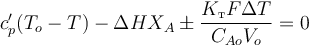
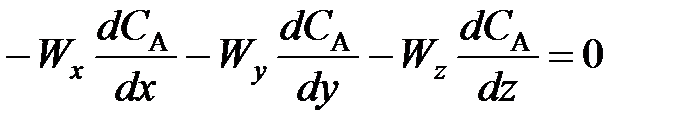 ; (77)
; (77)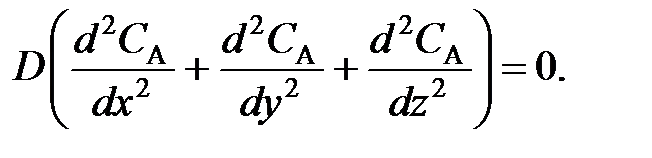 (78)
(78)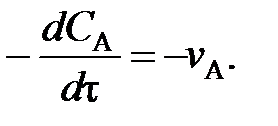 (79)
(79) . Поэтому перед
. Поэтому перед 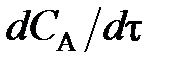 и vA ставят знак «–», чтобы скорость являлась положительной величиной.
и vA ставят знак «–», чтобы скорость являлась положительной величиной. (80)
(80)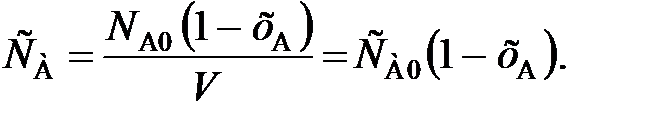 (81)
(81)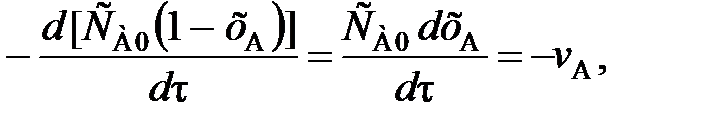 (82)
(82)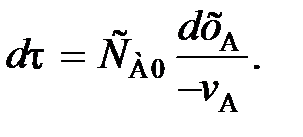 (83)
(83)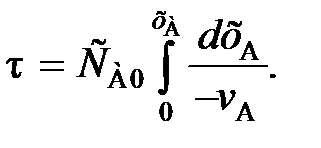 (84)
(84)
 (85)
(85)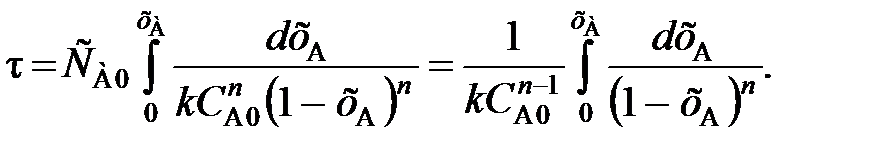 (86)
(86)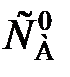 = k. (87)
= k. (87)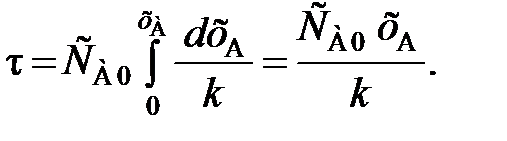 (88)
(88)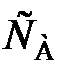 = k
= k 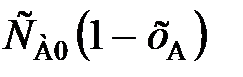 , (89)
, (89)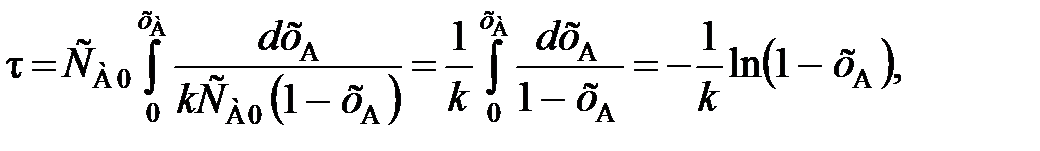 (90)
(90)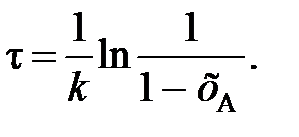 (91)
(91)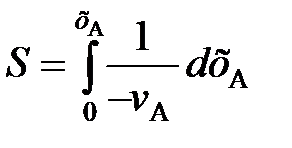 . (92)
. (92)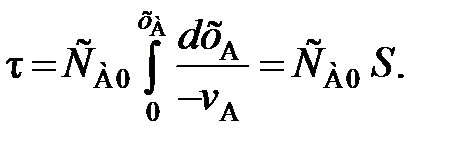 (93)
(93)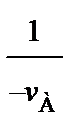
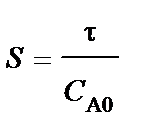
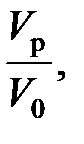 (94)
(94)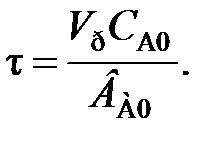 (95)
(95)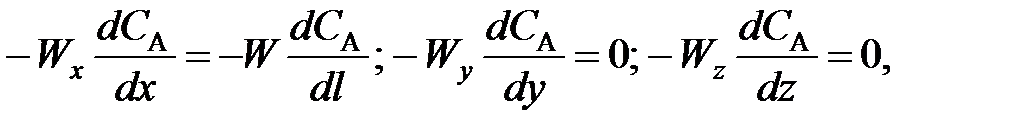 (96)
(96)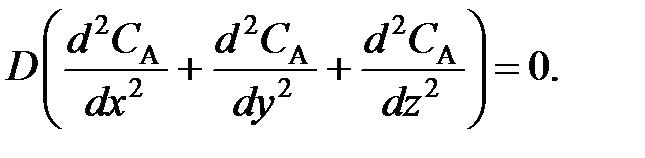 (97)
(97)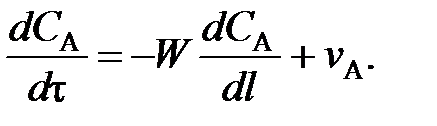 (98)
(98)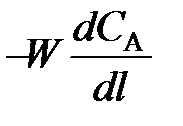 и от расхода вещества на химическую реакцию vА.
и от расхода вещества на химическую реакцию vА. (99)
(99)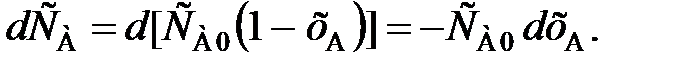 (100)
(100)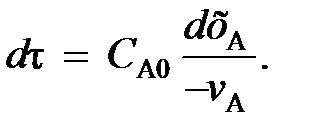 (102)
(102)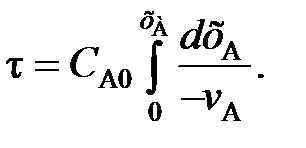 (103)
(103)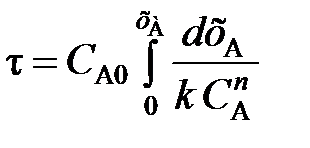 (104)
(104)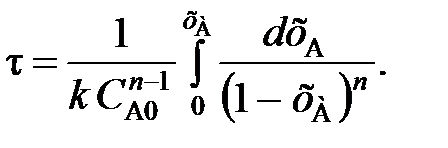 (105)
(105) (106)
(106)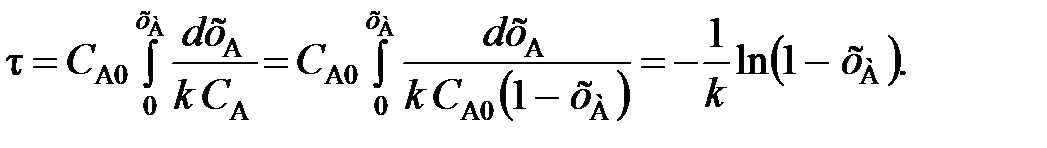 (107)
(107)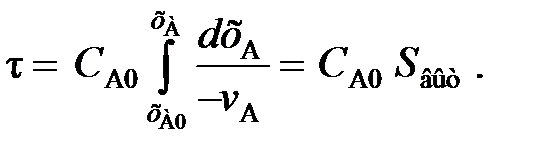 (108)
(108)
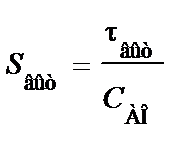
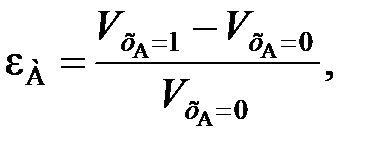 (109)
(109)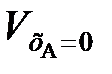 ,
, 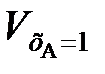 – объемы реакционной смеси соответственно при хА = 0 и хА = 1.
– объемы реакционной смеси соответственно при хА = 0 и хА = 1.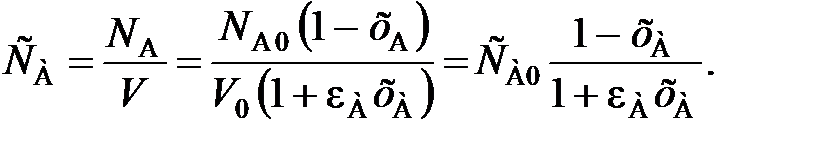 (111)
(111)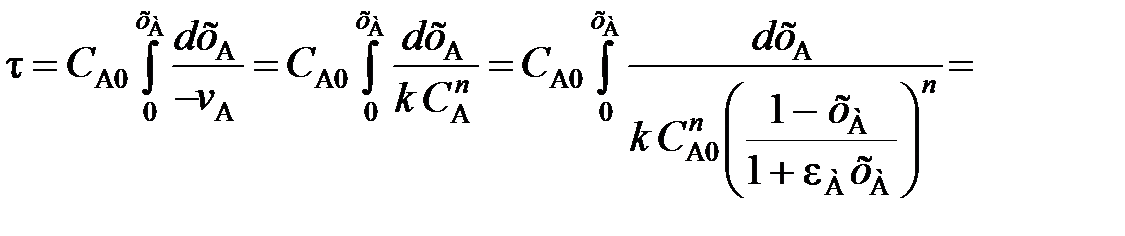
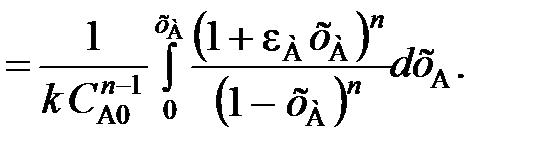 (112)
(112)















