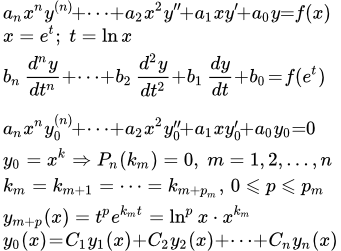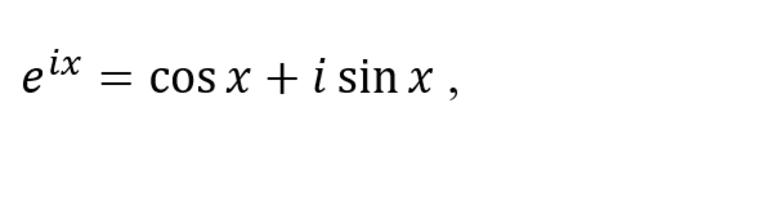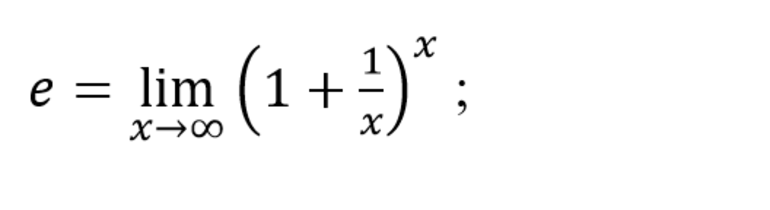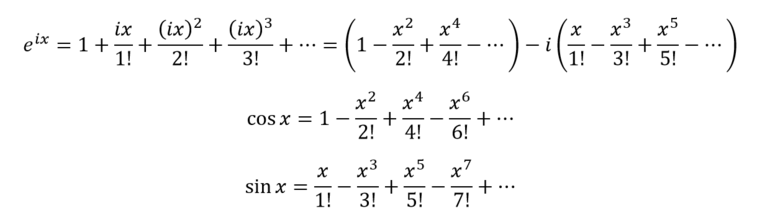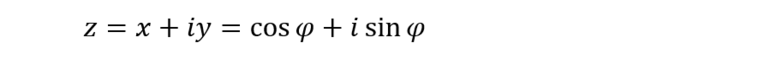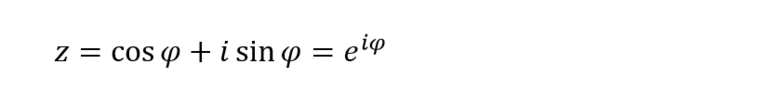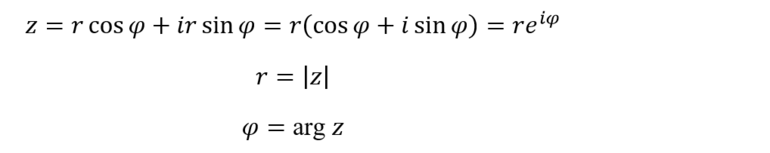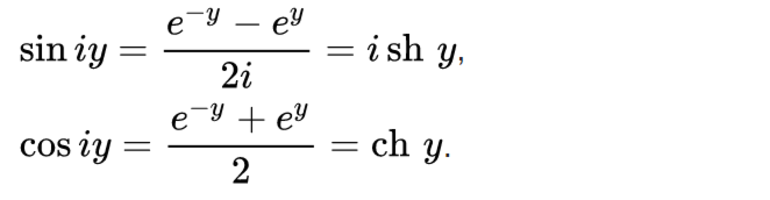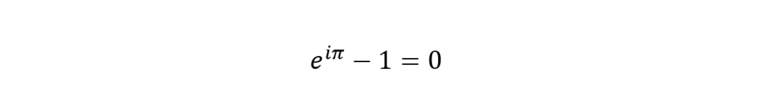Вывод формулы эйлера для дифференциальных уравнений

Более общее уравнение Эйлера имеет вид:
.
Это уравнение подстановкой t = ax+b приводится к более простому виду, которое мы и будем рассматривать.

Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Приведение дифференциального уравнения Эйлера к уравнению с постоянными коэффициентами.

Рассмотрим уравнение Эйлера:
(1) .
Оно сводится к линейному уравнению с постоянными коэффициентами подстановкой:
x = e t .
Действительно, тогда
;
;
;

;
;
.

Таким образом, множители, содержащие x m , сокращаются. Остаются члены с постоянными коэффициентами. Однако на практике, для решения уравнений Эйлера, можно применять методы решения линейных ДУ с постоянными коэффициентами без использования указанной выше подстановки.

Видео:Дифференциальное уравнение. Формула ЭйлераСкачать

Решение однородного уравнения Эйлера

Рассмотрим однородное уравнение Эйлера:
(2) .
Ищем решение уравнения (2) в виде
.
;
;
.
.
Подставляем в (2) и сокращаем на x k . Получаем характеристическое уравнение:
.
Решаем его и получаем n корней, которые могут быть комплексными.

Рассмотрим действительные корни. Пусть k_i – кратный корень кратности m . Этим m корням соответствуют m линейно независимых решений:
.

Рассмотрим комплексные корни. Они появляются парами вместе с комплексно сопряженными. Пусть k_i – кратный корень кратности m . Выразим комплексный корень k_i через действительную и мнимую части:
.
Этим m корням и m комплексно сопряженным корням соответствуют 2 m линейно независимых решений:
;
;
.
.

После того как получены n линейно независимых решений, получаем общее решение уравнения (2):
(3) .

Примеры

Видео:Линейное дифференциальное уравнение Коши-ЭйлераСкачать

Решение неоднородного уравнения Эйлера

Рассмотрим неоднородное уравнение Эйлера:
.
Метод вариации постоянных (метод Лагранжа) также применим и к уравнениям Эйлера.

Сначала мы решаем однородное уравнение (2) и получаем его общее решение (3). Затем считаем постоянные функциями от переменной x . Дифференцируем (3) n – 1 раз. Получаем выражения для n – 1 производных y по x . При каждом дифференцировании члены, содержащие производные приравниваем к нулю. Так получаем n – 1 уравнений, связывающих производные . Далее находим n -ю производную y . Подставляем полученные производные в (1) и получаем n -е уравнение, связывающее производные . Из этих уравнений определяем . После чего интегрируя, получаем общее решение уравнения (1).

Пример

Видео:06. Формула ЭйлераСкачать

Неоднородное уравнение Эйлера со специальной неоднородной частью

Рассмотрим уравнение Эйлера со специальной неоднородной частью:
(4)
,
где – многочлены от степеней и , соответственно.

Наиболее простой способ решения такого уравнения заключается в том, чтобы сделать подстановку
,
и решать линейное уравнение с постоянными коэффициентами со специальной неоднородной частью.

Автор: Олег Одинцов . Опубликовано: 14-08-2013 Изменено: 24-10-2020

Видео:Что такое формула Эйлера для комплексных чисел? Душкин объяснитСкачать

Формула Эйлера — доказательство, применение и примеры решения

Несмотря на простоту записи, эта формула несёт принципиально важную идею и находит применение почти во всех современных точных исследованиях и разработках.

Видео:✓ Формула Эйлера для графов и многогранников за 8 минут | Ботай со мной #103 | Борис ТрушинСкачать

Общие сведения

Формула Эйлера утверждает, что:

• i — мнимая единица, то есть корень квадратный из -1;
• e – экспонента, одна из важнейших математических констант, определяется выражением:

Формула, связывающая тригонометрические и функции экспоненциальные выражения, имеет множество применений. Она позволяет рассчитать некоторые выражения, решения которых невозможно или проблематично вычислить другим путём.

Необходимо лишь превратить исходные формулы в конструкцию, которая будет содержать удобные для проведения дальнейших операций функции.

Экспоненциальные и тригонометрические выражения обладают столь многочисленными свойствами, что имеют наиболее широкую область использования. Это делает неочевидную связь между ними особенно полезной.

История создания

Первым формулу опубликовал Роджер Котс, математик родом из Англии, в научном журнале, издаваемом Лондонским королевским обществом. Затем, формула была отображена в книге «Гармония мер», которую издали после смерти автора — в 1722 году. Котс не придал ей большого значения и отобразил среди геометрических построений. Чтоб полученное Котсом выражение приобрело привычный вид, необходимо исправить ошибку в знаке и перевести на современный язык описания математики.

Формулу в привычном для людей виде опубликовал Эйлер в статье 1740 года. В 1748 году выражение было также представлено в его книге «Введение в анализ бесконечно малых». Эйлер доказал формулу на основе бесконечных разложений составляющих формулы в степенные ряды.

Но учёные того времени не рассматривали геометрической интерпретации формулы, которая используется на сегодняшний день. Представление о комплексных числах в виде точек на комплексной плоскости, на основе которого строится геометрическая интерпретация равенства, появилось примерно на 50 лет позже в работах К. Весселя.

Доказательство формулы

Вывод формулы Эйлера можно выполнить, используя ряд Маклорена – частный случай ряда Тейлора при разложении функции в окрестности точки x=0. Раскладывая левую часть равенства, получится cтепенной ряд, в котором в различные степени будет возводиться мнимая единица. Необходимо вынести её, сформировав коэффициент перед x.

При расчёте степеней мнимой единицы удаётся получить интересный эффект: если степень чётная – можно её представить как умножение некоторого числа пар i*i, которые можно заменить на -1 (из определения мнимой единицы). А при умножении между собой отрицательных единиц возможны два случая, опять же исходя из чётности их количества. Если их число кратно 2, то получают просто единицу («минус на минус даёт плюс»). Если их нечётное число – получится -1.

С другой стороны, из всех членов, где мнимая единица стоит в нечётной степени, она выносится за скобки. В них останется выражение, подобное тому, которое вышло для чётных степеней.

Таким образом, чередование происходит дважды: по чётности степеней мнимой единицы, а следом – по чётности степеней -1, которые были получены вследствие первого шага. Получается циклическое изменение на каждые четыре члена суммы.

После разделения мнимых и вещественных членов последовательности и расстановки чередующихся знаков формируются две группы слагаемых, которые представляют собой разложения других функций – синуса и косинуса. При их подстановке получится равенство Эйлера.

Видео:Метод ЭйлераСкачать

Использование

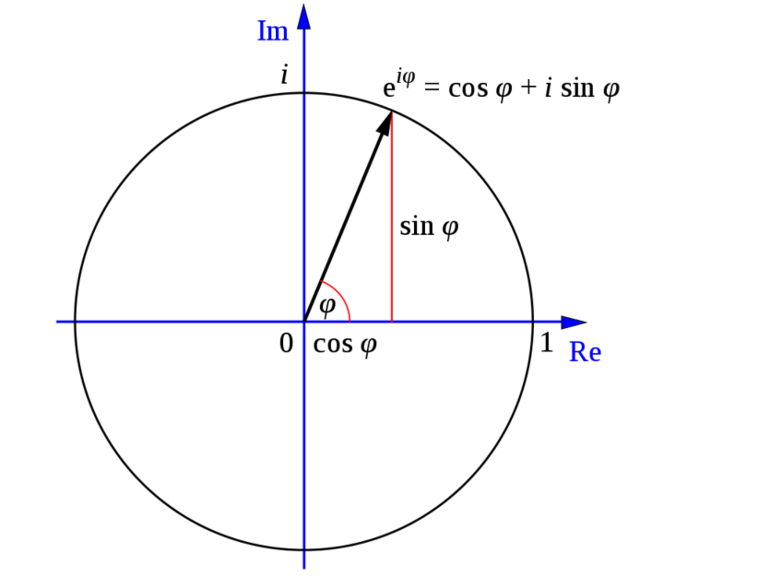
Геометрическая интерпретация позволяет наглядно отобразить математические преобразования. Для этой цели используется комплексная плоскость. Она геометрически отображает комплексные величины: вдоль горизонтальной оси откладывается вещественная часть числа, а вдоль вертикальной – мнимая. Таким образом, число отражается точкой с координатами, представляющими собой вещественную (Re) и мнимую (Im) его части. Часто для удобства используется вектор, проведённый из начала координат в эту точку (радиус-вектор). Несложно понять, что его координаты совпадают с координатами той самой точки.

В геометрической интерпретации рассматривается единичная окружность (радиус равен единице). Для любой точки, принадлежащей окружности, можно построить прямоугольные треугольники, опуская перпендикуляры на оси координат. Это позволяет сделать переход в полярную систему координат, которая удобна для пояснения другой формы числа.

В ней положение точки определяется не расстояниями, отложенными на осях, а длиной вектора, проведённого в точку из начала координат и углом поворота относительно оси (вещественной).

Из свойств прямоугольного треугольника следует, что синус используемого угла равен отношению мнимой части числа (противолежащего катета) к длине вектора (гипотенузе). Так как длина гипотенузы равна единице (радиус окружности), то мнимая часть числа равна синусу угла. Аналогично вдоль вещественной оси откладывается расстояние, равное косинусу этого угла. Теперь для получения числа в новом виде осталось только сложить его части, не забыв умножить мнимую на i. Таким образом, исходное число равно:

Последняя конструкция в точности повторяет выражение, стоящее в правой части равенства Эйлера. Значит, благодаря ей появляется возможность отобразить комплексную величину по-новому – через экспоненту:

Комплексный анализ

Формула играет важную роль в комплексном анализе. На её основе строится связь тригонометрической и показательной форм записи комплексного числа, которая отображена в только что полученной формуле.

Нельзя ограничиваться единичной окружностью. Как отобразить любую точку комплексной плоскости в новом виде? Можно это представить очень просто: будет изменяться радиус. Тогда числа, выраженные через синус и косинус, будут умножаться на длину гипотенузы (радиус окружности). Эта длина называется модулем комплексной величины, а угол поворота – аргументом.

Модуль обозначается так же, как и обычный модуль для вещественного числа, ведь он представляет просто более общий случай. В то же время для аргумента стало использоваться новое обозначение – arg.

И синус, и косинус умножаются на модуль. Следовательно, его можно вынести за скобки. Что осталось в скобках? – Всё та же правая часть любимой формулы. Можно заменить содержимое скобок на экспоненту.

Таким образом, имеется три формы записи комплексного числа:

• алгебраическая;
• тригонометрическая;
• показательная.

Последние две связаны между собой за счёт формулы Эйлера. Зачем их три? Новичку, как правило, приятно использовать алгебраическую, ведь она проще выглядит: лишь сумма двух чисел. Но некоторые операции очень сложно либо даже невозможно осуществить, используя лишь её.

Так что часто приходится переводить число из алгебраической формы в тригонометрическую, которая имеет ряд полезных особенностей. А вот перейти к показательной форме от тригонометрической не составит труда – копируется аргумент числа и вставляется в степень e, умножив на i.

Производные формулы

Формула Эйлера выражает экспоненту через тригонометрические функции, но можно получить и обратное преобразование. Применимость её для таких целей очевидна. Заменяют x на –x. Косинус – чётная функция, синус – нечётная. В результате замены происходит изменение знака перед синусом.

Сложение и вычитание полученных выражений приводит к уравнению, с одной стороны которого располагается удвоенный косинус или синус, а с другой – комбинация экспонент. Выразить отсюда тригонометрическую функцию не составит труда.

Эти формулы имеют большое значение при работе с преобразованиями комплексных величин. Например, они могут служить определением тригонометрических функций комплексной переменной.

При обычном рассмотрении тригонометрических функций не удаётся получить значения для комплексного аргумента, зато есть возможность поставить такое значение в только что полученную формулу. В результате преобразований можно получить значение, которое выражается лишь через косинусы и синусы вещественной переменной, а также гиперболические косинусы и синусы, опять же, с вещественными аргументами.

Таким образом, для получения значений ряда функций комплексных используются следствия формулы Эйлера.

Пример применения:

Также эти формулы значительно упрощают некоторые расчёты. С их помощью можно получить многие тригонометрические тождества путём проведения преобразований и дальнейшей обратной замены.

Кроме того, из формулы вытекает известное тождество Эйлера, которое связывает пять фундаментальных математических констант. Оно представляет собой частный случай при x=π. При подстановке числа π синус обращается в 0, а косинус принимает значение 1.

Остаётся лишь перенести 1 в другую часть уравнения, чтоб получить все пять констант в явном виде.

Тождество было опубликовано Эйлером в 1740 году и вызвало общественный резонанс. Имели место даже попытки мистического толкования как символа единства математики. Ведь тождество связывает величины, произошедшие из разных разделов математики:

• нуль и единица — из арифметики;
• число π — геометрии;
• мнимая единица (i) — алгебры;
• число Эйлера (е) — из математического анализа.

Наглядное доказательство

Существуют альтернативные доказательства, как для почти любых математических выражений. Более наглядное отображение может дать рассмотрение производной выражения в показательной форме, а именно от числа с модулем, равным единице.

Производная экспоненты равна той же самой экспоненте, но с одним изменением: необходимо умножить её значение, на которое умножался аргумент в степени.

Умножение на i аналогично повороту на 90 градусов. Полученный угол даёт возможность провести аналогию с центростремительной силой – подтверждается то, что точка движется по окружности с центром в начале координат. Но в то же время, для этой же окружности действует отображение точек через сумму косинуса и синуса. Отсюда вытекает взаимное соответствие комплексной экспоненты и тригонометрических функций.

В науке и технике

В комплексном анализе для возведения числа в степень его переводят в тригонометрическую или показательную форму. Например, возведение в степень комплексного числа в тригонометрической форме легко произвести, пользуясь формулой Муавра. Тем не менее, показательная форма позволяет сократить объёмы записей, не усложняя их. Так что имеет смысл проводить промежуточные расчёты, используя именно её. Хотя для простых случаев есть возможность просто вычислять корни и степени с помощью онлайн-калькуляторов. Они тоже используют переходы между формами комплексного числа.

Согласно формуле Муавра, при возведении комплексного числа в степень необходимо возвести в эту степень модуль числа и умножить аргумент на тот же показатель степени. Для вычисления корня производятся аналогичные операции: взятие корня и деление соответственно.

Но для получения всех корней необходимо учитывать возможность сдвига аргумента 2π и кратные ему значения (при повороте на полный оборот попадают в ту же точку – то же число). В связи с этим, при взятии корня образуется также множество результатов, но сдвиг между ними в равное показателю корня раз меньший. Следовательно, на каждый оборот приходится несколько корней, что необходимо учитывать в большинстве расчётов.

Ещё более широкие перспективы открываются благодаря свойству экспоненты при дифференцировании и интегрировании переходить самой в себя. Задачи решаются на порядок проще, чем при проведении вычислений с тригонометрическими функциями. Как следствие, показательная форма комплексного числа и формула Эйлера широко применяются в физике и технике, а также множестве программных алгоритмов.

Видео:Дифференциальное уравнение Эйлера. Основное уравнение гидростатикиСкачать

Вывод формулы эйлера для дифференциальных уравнений

Пример 2.1. Рассмотрим пример, который легко решить аналитически. Требуется найти экстремум функционала

при граничных условиях

Найдём частные производные и

Вычислим полную производную по x от

Составляем дифференциальное уравнение Эйлера вида

или, после упрощений

Его общее решение имеет вид

Для нахождения произвольных постоянных C₁ и C₂ подставим решение (2.16) в граничные условия (2.11):

Видно, что система (2.17) имеет единственное решение. Решая эту систему, найдём значения C₁ и C₂:

и тогда уравнение экстремали имеет вид:

Действительно ли на этой кривой достигается экстремум? И если да, то какой: минимум или максимум? Далее, в главе 13, мы рассмотрим достаточные условия экстремума . В частности, мы выведем условие Лежандра: если на экстремали выполняется условие а на функциях, близких к экстремали, для произвольных y‘ имеет место то достигается сильный минимум. В нашем случае это выполняется:

и, следовательно, на нашей экстремали достигается сильный минимум. Проверим этот результат: вычислим на нескольких функциях вида Эти функции удовлетворяют граничным условиям (2.11) и, следовательно, являются допустимыми. Для вычислений применим MATLAB.

Действительно, полученный результат не противоречит выводу о том, что на функции достигается минимум. Но, конечно же, проведенная проверка не доказывает этот факт. Ведь мы проверили только несколько из бесконечного числа функций, графики которых проходят через точки и Доказательством могут служить необходимые и достаточные условия экстремума функционала.

Пример 2.2. Найти экстремаль функционала

при граничных условиях

Выводим уравнение Эйлера вида (2.9). Частные производные:

Уравнение Эйлера после упрощений имеет вид:

Его общее решение

Находим произвольные постоянные из граничных условий (3.22). Подставляем решение (3.25) в эти граничные условия:

Мы видим, что из полученной системы уравнений можно найти только а C₂ может быть произвольной. Поэтому данная вариационная задача имеет бесчисленное множество решений вида

На любой из этих функций функционал принимает постоянное значение (какое − мы сейчас посчитаем). Проверка по достаточному условию Лежандра даёт:

поэтому на экстремалях (3.27) достигается сильный минимум.

Посчитаем значение функционала (2.21) на функциях вида (2.27) и нарисуем несколько экстремалей с помощью MATLAB.

На каждой из наших функций функционал равен нулю.

Видео:Численное решение задачи Коши методом ЭйлераСкачать

2.2. Частные случаи уравнений Эйлера

Иногда решение уравнения Эйлера существенно упрощается. Рассмотрим соответствующие частные случаи.

2.2.1. Подынтегральная функция F не зависит явно от y‘

Материал этого подраздела изложен в книге.

2.2.2. Подынтегральная функция F линейно зависит от y‘

Материал этого подраздела изложен в книге.

2.2.3. Подынтегральная функция F не зависит явно от y

Материал этого подраздела изложен в книге.

2.2.4. Подынтегральная функция F зависит только от y‘

Материал этого подраздела изложен в книге.

2.2.5. Подынтегральная функция F не зависит явно от x

Материал этого подраздела изложен в книге.

Видео:Формула ЭйлераСкачать

2.3. Вопросы для самопроверки

1. Какую вариационную задачу мы решаем?
2. Как выводится дифференциальное уравнение Эйлера?
3. Где используется в выводе дифференциального уравнения Эйлера основная лемма вариационного исчисления?
4. Почему обращается в нуль внеинтегральное слагаемое в формуле (2.8) при интегрировании по частям?
5. Чем отличается частная производная от полной?
6. Какие Вы знаете методы решения дифференциальных уравнений порядка?
7. Всегда ли решение вариационной задачи будет единственным? От чего это зависит?
8. Какие частные случаи уравнения Эйлера Вы знаете?
9. В каких случаях уравнение Эйлера перестаёт быть дифференциальным и становится конечным?
10. В каких случаях вариационная задача теряет смысл?
11. Как записывается интеграл уравнения Эйлера, если подынтегральная функция F не зависит явно от y?
12. Каким будет решение уравнения Эйлера, если подынтегральная функция F зависит только от y‘?
13. Как решается уравнение Эйлера, если подынтегральная функция F не зависит явно от y‘?
14. Как решается задача о брахистохроне?

Видео:#161. САМАЯ КРАСИВАЯ ФОРМУЛА В МАТЕМАТИКЕ — ФОРМУЛА ЭЙЛЕРА: e^(iπ)+1=0Скачать

2.4. Примеры выполнения заданий

2.4.1. Задание 1

Найти экстремаль функционала

Исследовать полученную экстремаль на достаточные условия экстремума. Вычислить значение функционала на найденной экстремали и, для сравнения, на прямой, соединяющей точки и Построить график решения.

В этом примере подынтегральная функция является функцией общего вида, поэтому составим уравнение Эйлера в виде (2.9) и решим его. Затем построим график решения. Попутно исследуем на выполнение достаточных условий экстремума и вычислим значение функционала на экстремали и отрезке прямой M₁M₂. Применим для решения задачи MATLAB.

Очистим память. Напечатаем заголовок решаемой задачи. Если хотите, задайте другую строку для вывода (например, свою фамилию). Опишем символические переменные [58]. Для решения уравнения Эйлера используем принятые в MATLAB обозначения производных: Dy для y‘ и D2y для y». Аргумент обозначим x , а функцию − y .

Вводим подынтегральную функцию и граничные условия. Печатаем их. Здесь вы должны поставить свои исходные данные: подынтегральную функцию F и граничные условия x₁, y₁, x₂, y₂.

Начинаем вывод дифференциального уравнения Эйлера (2.9). Найдём частные производные F_y и F_y’. Напечатаем их.

В уравнение Эйлера (2.9) входит полная производная Вычислим её по обычной формуле дифференцирования сложной функции:

Напечатаем её. Напечатаем также величину необходимую для проверки достаточных условий экстремума по признаку Лежандра.

Составим левую часть дифференциального уравнения Эйлера (2.9) и упростим её. Преобразуем символическую переменную Euler в строку.

Мы составили уравнение Эйлера, теперь решим его. Команда dsolve позволяет находить как общее решение дифференциального уравнения, так и частное его решение, удовлетворяющее заданным начальным или граничным условиям. В следующих главах при решении других заданий нам нужно будет иметь общее решение уравнения Эйлера. Найдём его.

Сформируем теперь уравнения для граничных условий. Подставим в найденное аналитическое решение Sol граничные точки x1 и x2 , и приравняем их соответственно y1 и y2 .

Решаем полученную систему конечных уравнений − находим значения произвольных постоянных C1 и C2 . Присваиваем найденные решения символическим константам, полученным при решении дифференциального уравнения. Теперь вычисляем аналитическое решение Sol21 . Такое вычисление сводится к тому, что в него будут подставлены найденные значения констант C1 и C2 . Печатаем найденное уравнение экстремали.

Вычислим значения функционала (2.86) на найденной экстремали и на прямой, соединяющей точки M₁ и M₂. Подставим в подынтегральную функцию F аналитические выражения для этих линий и их производных, а затем проинтегрируем. Напечатаем результаты.

В данном примере условие Лежандра говорит о сильном минимуме, что подтверждается полученным результатом: значение функционала на экстремали меньше, чем на другой допустимой функции. А как в вашем варианте: какой экстремум достигается? И подтверждается ли этот результат сравнением величин Jextr и Jlin ? Если нет, то не забудьте, что найденный экстремум − только локальный, а не глобальный! Попробуйте вычислить значение функционала не на прямой M₁M₂, а на какой-нибудь другой допустимой кривой, достаточно близкой к экстремали. Например, можно наложить на экстремаль несколько полуволн синусоиды, смещённой и деформированной вдоль оси Ox так, что

И, наконец, строим график. Задаём массив аргументов для рисования графика функции и вычисляем значения функции. Рисуем график, подписываем заголовок и координатные оси установленным шрифтом.

2.4.2. Задание 2

Найти экстремаль функционала

Исследовать на выполнение достаточных условий экстремума. Построить график решения.

В этом примере подынтегральная функция не зависит явно от y. Первый интеграл уравнения Эйлера имеет вид (2.43). Составим программу для решения этой вариационной задачи. Вначале введём исходные данные. У нас будет первый интеграл уравнения Эйлера, поэтому ни сама функция y, ни её вторая производная y» нам не нужны, и мы их не описываем. Поставьте свою подынтегральную функцию и граничные условия.

Строим первый интеграл и решаем полученное дифференциальное уравнение. Названия констант C1 и C2 используются в команде dsolve , поэтому при составлении интеграла уравнения Эйлера обозначим константу C . Все использованные здесь функции и операторы MATLAB были описаны ранее, в примере 1.

В переменной Sol получено общее решение, произвольные постоянные обозначены C и C1 . Найдём их. Для этого подставим в Sol граничные точки. Приравняем полученные выражения соответственно y1 и y2 . Тем самым мы сформируем систему уравнений.

Решим полученную систему − найдём произвольные постоянные C и C1 . Подставим их в решение Sol . Ограничим решение 14 знаками. Напечатаем уравнение найденной экстремали.

Дальнейшие действия не отличаются от описанных в примере 1. Рисуем график и и вычисляем F_y’y’, которая нужна для проверки достаточных условий экстремума по признаку Лежандра.

Проанализируйте достаточное условие Лежандра. Достигается ли экстремум на вашей экстремали? Если да, то какой?

2.4.3. Задание 3

Решить задачу о брахистохроне, соединяющей точки и

Мы уже решили эту задачу аналитически. Нам осталось найти значение константы C₁ и параметра в конечной точке t₂ из решения системы уравнений (2.84). Составим программу для решения этого примера. Вначале введём исходные данные задачи. Подставьте свою правую точку.

Составляем систему уравнений (2.84). Левую часть каждого уравнения мы задаём сразу в виде строки. В правой части переводим числа x2 и y2 в их строковые представления с помощью функции num2str . Ранее мы использовали конструкцию char(sym(y2)) . Оба варианта работают правильно − вы можете это проверить. Решаем полученную систему уравнений аналитически. Печатаем решения.

Рисуем график полученной брахистохроны. Выбираем начало координат в левом верхнем углу с помощью команды axis . Задаём границы по оси Ox, чтобы график занимал всё место на рисунке. Выравниваем масштабы по осям координат, чтобы брахистохрона выглядела неискажённой. Надписываем заголовок и метки осей.

Видео:Численные методы решения ДУ: метод ЭйлераСкачать

2.5. Задание

Для своего варианта функционалов 1, 2, 3 найти экстремали, построить их графики и исследовать на выполнение достаточных условий экстремума.

💡 Видео

#Дифуры II. Урок 5. Уравнение ЭйлераСкачать

7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Решение ОДУ методом Эйлера (программа)Скачать

МЗЭ 2022 Численное решение дифференциальных уравнений. Неявный метод Эйлера. Ложкин С.А.Скачать

Устойчивость стержня. Формула ЭйлераСкачать

Формула Эйлера: объяснение | Самая красивая формула математики – Алексей Савватеев | ЛекцииСкачать

Пример решения задачи Коши методом Эйлера. Метод Эйлера с пересчетом.Скачать