- п.1. Понятие асимптоты
- п.2. Вертикальная асимптота
- п.3. Горизонтальная асимптота
- п.4. Наклонная асимптота
- п.5. Алгоритм исследования асимптотического поведения функции
- п.6. Примеры
- Асимптоты графика функции
- Виды асимптот
- Нахождение наклонной асимптоты
- Асимптоты
- Вертикальная асимптота.
- Асимптота (невертикальная асимптота).
- 🌟 Видео
п.1. Понятие асимптоты
Различают вертикальные, горизонтальные и наклонные асимптоты.
Например:
 Вертикальная асимптота x=3 |  Горизонтальная асимптота y=1 |
 Наклонная асимптота y=x | |
п.2. Вертикальная асимптота
Таким образом, практически каждой точке разрыва 2-го рода (см. §40 данного справочника) соответствует вертикальная асимптота.
Вертикальных асимптот может быть сколько угодно, в том числе, бесконечное множество (например, как у тангенса – см. §6 данного справочника).
Например:
Исследуем непрерывность функции (y=frac)
ОДЗ: (xne left)
(leftnotin D) — точки не входят в ОДЗ, подозрительные на разрыв.
Исследуем (x_0=-3). Найдем односторонние пределы: begin lim_frac=frac=frac=+infty\ lim_frac=frac=frac=-infty end Односторонние пределы не равны и бесконечны.
Точка (x_0=-3) — точка разрыва 2-го рода.
Исследуем (x_1=1). Найдем односторонние пределы: begin lim_frac=frac=frac=-infty\ lim_frac=frac=frac=+infty end Односторонние пределы не равны и бесконечны.
Точка (x_1=1) — точка разрыва 2-го рода.
Вывод: у функции (y=frac) две точки разрыва 2-го рода (left), соответственно – две вертикальные асимптоты с уравнениями (x=-3) и (x=1).
п.3. Горизонтальная асимптота
Число горизонтальных асимптот не может быть больше двух.
Например:
Исследуем наличие горизонтальных асимптот у функции (y=frac)
Ищем предел функции на минус бесконечности: begin lim_frac=frac=+0 end На минус бесконечности функция имеет конечный предел (b=0) и стремится к нему сверху (о чем свидетельствует символическая запись +0).
Ищем предел функции на плюс бесконечности: begin lim_frac=frac=+0 end На плюс бесконечности функция имеет тот же конечный предел (b=0) и также стремится к нему сверху.
Вывод: у функции (y=frac) одна горизонтальная асимптота (y=0). На плюс и минус бесконечности функция стремится к асимптоте сверху.
Итоговый график асимптотического поведения функции (y=frac):
п.4. Наклонная асимптота
Число наклонных асимптот не может быть больше двух.
Чтобы построить график асимптотического поведения, заметим, что у функции (y=frac), очевидно, есть вертикальная асимптота x=1. При этом: begin lim_frac=-infty, lim_frac=+infty end
График асимптотического поведения функции (y=frac):
п.5. Алгоритм исследования асимптотического поведения функции
На входе: функция (y=f(x))
Шаг 1. Поиск вертикальных асимптот
Исследовать функцию на непрерывность. Если обнаружены точки разрыва 2-го рода, у которых хотя бы один односторонний предел существует и бесконечен, сопоставить каждой такой точке вертикальную асимптоту. Если таких точек не обнаружено, вертикальных асимптот нет.
Шаг 2. Поиск горизонтальных асимптот
Найти пределы функции на плюс и минус бесконечности. Каждому конечному пределу сопоставить горизонтальную асимптоту. Если оба предела конечны и равны, у функции одна горизонтальная асимптота. Если оба предела бесконечны, горизонтальных асимптот нет.
Шаг 3. Поиск наклонных асимптот
Найти пределы отношения функции к аргументу на плюс и минус бесконечности.
Каждому конечному пределу k сопоставить наклонную асимптоту, найти b. Если только один предел конечен, у функции одна наклонная асимптота. Если оба значения k конечны и равны, и оба значения b равны, у функции одна наклонная асимптота. Если оба предела для k бесконечны, наклонных асимптот нет .
На выходе: множество всех асимптот данной функции.
п.6. Примеры
Пример 1. Исследовать асимптотическое поведение функции и построить схематический график:
a) ( y=frac )
1) Вертикальные асимптоты
Точки, подозрительные на разрыв: (x=pm 1)
Односторонние пределы в точке (x=-1) begin lim_frac=frac=frac=-infty\ lim_frac=frac=frac=+infty end Точка (x=-1) — точка разрыва 2-го рода
Односторонние пределы в точке (x=1) begin lim_frac=frac=frac=-infty\ lim_frac=frac=frac=+infty end Точка (x=1) — точка разрыва 2-го рода
Функция имеет две вертикальные асимптоты (x=pm 1)
График асимптотического поведения функции (y=frac)
2) Горизонтальные асимптоты
Пределы функции на бесконечности: begin b_1=lim_e^<frac>=e^0=1\ b_2=lim_e^<frac>=e^0=1\ b=b_1=b_2=1 end Функция имеет одну горизонтальную асимптоту (y=1). Функция стремится к этой асимптоте на минус и плюс бесконечности.
График асимптотического поведения функции (y=e^<frac>)
в) ( y=frac )
Заметим, что ( frac=frac=frac=frac ) $$ y=fracLeftrightarrow begin y=frac\ xne -1 end $$ График исходной функции совпадает с графиком функции (y=frac), из которого необходимо выколоть точку c абсциссой (x=-1).
3) Наклонные асимптоты
Ищем угловые коэффициенты: begin k_1=lim_frac=left[fracright]=lim_frac<x^2left(1+fracright)>=frac=1\ k_2=lim_frac=left[fracright]=lim_frac<x^2left(1+fracright)>=frac=1\ k=k_1=k_2=1 end У функции есть одна наклонная асимптота с (k=1).
Ищем свободный член: begin b=lim_(y-kx)= lim_left(frac-2right)= lim_frac= lim_frac=left[fracright]=\ =lim_frac=frac=1 end Функция имеет одну наклонную асимптоту (y=x+1).
График асимптотического поведения функции (y=frac)
2) Горизонтальные асимптоты
Пределы функции на бесконечности: begin b_1=lim_xe^<frac>=-inftycdot e^0=-infty\ b_2=lim_xe^<frac>=+inftycdot e^0=+infty end Оба предела бесконечны.
Функция не имеет горизонтальных асимптот.
График асимптотического поведения функции (y=xe^<frac>)
Видео:Асимптоты функции. Наклонная асимптота. 10 класс.Скачать

Асимптоты графика функции
Видео:Математика без Ху!ни. Нахождение асимптот, построение графика функции.Скачать

Виды асимптот
Прямая $x=x_$ называется вертикальной асимптотой графика функции $y=f(x)$, если хотя бы одно из предельных значений $lim _<x rightarrow x_-0> f(x)$ или $lim _<x rightarrow x_+0> f(x)$ равно $+infty$ или $-infty$ .
Замечание. Прямая $x=x_$ не может быть вертикальной асимптотой, если функция непрерывна в точке $x=x_$ . Поэтому вертикальные асимптоты следует искать в точках разрыва функции.
Прямая $y=y_$ называется горизонтальной асимптотой графика функции $y=f(x)$, если хотя бы одно из предельных значений $lim _ f(x)$ или $lim _ f(x)$ равно $y_$ .
Замечание. График функции может иметь только правую горизонтальную асимптоту или только левую.
Прямая $y=k x+b$ называется наклонной асимптотой графика функции $y=f(x)$, если $lim _[f(x)-k x-b]=0$
Видео:Математический анализ, 15 урок, АссимптотыСкачать

Нахождение наклонной асимптоты
(условиях существования наклонной асимптоты)
Если для функции $y=f(x)$ существуют пределы $lim _ frac=k$ и $lim _[f(x)-k x]=b$, то функция имеет наклонную асимптоту $y=k x+b$ при $x rightarrow infty$ .
Горизонтальная асимптота является частным случаем наклонной при $k=0$ .
Если при нахождении горизонтальной асимптоты получается, что $lim _ f(x)=infty$, то функция может иметь наклонную асимптоту.
Кривая $y=f(x)$ может пересекать свою асимптоту, причем неоднократно.
Задание. Найти асимптоты графика функции $y(x)=frac<x^-3 x+2>$
Решение. Область определения функции:
$D[f] : x in(-infty ;-1) cup(-1 ;+infty)$
а) вертикальные асимптоты: прямая $x=-1$ — вертикальная асимптота, так как
то есть, горизонтальных асимптот нет.
в) наклонные асимптоты $y=k x+b$:
Таким образом, наклонная асимптота: $y=x-4$ .
Ответ. Вертикальная асимптота — прямая $x=-1$ .
Видео:Асимптоты функции. Горизонтальная асимптота. 10 класс.Скачать

Асимптоты
Видео:Установление эмпирической и молек. формул по массовым долям элем., входящих в состав в-ва. 10 класс.Скачать

Вертикальная асимптота.
Если выполнено хотя бы одно из условий
$$
lim_<xrightarrow x_-0>f(x)=infty,qquadlim_<xrightarrow x_+0>f(x)=infty,nonumber
$$
то прямую (x=x_) называют вертикальной асимптотой графика функции (y=f(x)).
Например, прямая (x=0) — вертикальная асимптота графиков функций (y=displaystyle frac), (y=operatornamex^2), (y=displaystyle frac<x^>), (y=operatornamex), прямая (x=-1) — вертикальная асимптота графика функции (y=displaystyle frac), прямые (x=displaystyle frac +pi k (kin mathbb)) — вертикальные асимптоты графика функции (y=operatornamex).
| Асимптота | Функция | График функции |
| (x=0) | (y=displaystyle frac) | |
| (y=operatornamex^2) | | |
| (y=displaystyle frac<x^>) | | |
| (y=operatornamex) | | |
| (x=-1) | (y=displaystyle frac) | |
Видео:Асимптоты графика функции. Практика. Пример 1.Скачать

Асимптота (невертикальная асимптота).
Прямую
$$
y=kx+bnonumber
$$
называют асимптотой (невертикальной асимптотой) графика функции (y=f(x)) при ( xrightarrow+infty), если
$$
lim_(f(x)-(kx+b))=0.label
$$
Если (kneq 0), то асимптоту называют наклонной, а если (k=0), то асимптоту (y=b) называют горизонтальной.
Аналогично вводится понятие асимптоты при (xrightarrow-infty).
Например, прямая (y=0) — горизонтальная асимптота графиков функции (y=displaystyle frac), (y=displaystyle frac<x^>) при (xrightarrow +infty) и (xrightarrow -infty), графика функции (y=a^x, a > 1)), при (xrightarrow -infty). Прямая (y=1) — асимптота графиков функций (y=e^), (y=operatorname
| Асимптота | Функция | График функции |
| (y=1) | (y=e^) | |
| (y=operatorname | x) | |
|---|---|---|
| (y=operatornamex) | | |
| (y=displaystyle frac) | (y=operatornamex) | |
| (y=pi) | (y=operatornamex) | |
Найти асимптоту при (xrightarrow+infty) и (xrightarrow-infty) графика функции:
- (triangle) Так как (y=-2+displaystyle frac), то прямая (y=-2) — асимптота графика (y=displaystyle frac) (рис. 9.4) при (xrightarrow+infty) и (xrightarrow-infty).
(y=displaystyle frac)
- Разделив числитель (x^) на знаменатель ((x+1)^2) по правилу деления многочленов (можно воспользоваться равенством (x^=((x+1)-1)^=(x+1)^-3(x+1)^+3(x+1)-1)), получим
$$
frac<x^><(x+1)^>=x-2+frac<(x+1)^>.label
$$
Отсюда следует, что асимптотой графика функции (y=displaystyle frac<x^><(x+1)^>) при (xrightarrow+infty) и (xrightarrow-infty) является прямая (y=x-2). - Используя равенство (y=displaystyle sqrt[3]<x^+x^>=xleft(1+fracright)^) и локальную формулу Тейлора, получаем (y=xleft(1+displaystyle frac+oleft(fracright)right)=x+frac+o(1)) при (xrightarrow 0), откуда следует, что прямая (y=x+displaystyle frac) — асимптота графика функции (y=sqrt[3]) при (xrightarrow+infty) и (xrightarrow-infty).
- Применяя формулу Тейлора для экспоненты, получаем (y=left(x-displaystyle fracright)left(1-frac+oleft(fracright)right)=x-frac+o(1)) при (xrightarrow infty), откуда следует, что (y=x-displaystyle frac) — асимптота графика данной функции при (xrightarrow+infty) и (xrightarrow-infty). (blacktriangle)
Для того, чтобы прямая (y=kx+b) была асимптотой графика функции (y=f(x)) при ( xrightarrow+infty), необходимо и достаточно, чтобы существовали конечные пределы
$$
lim_frac=k,label
$$
$$
displaystyle lim_(f(x)-kx)=b.label
$$
(circ) Необходимость. Если прямая (y=kx+b) — асимптота графика функции (y=f(x)) при (xrightarrow+infty), то выполняется условие eqref или равносильное ему условие
$$
f(x)=kx+b+alpha(x),quad alpha(x)rightarrow 0 quad при quad xrightarrow +infty.label
$$
Разделив обе части равенства eqref на (x), получим
$$
frac=k+frac+frac,nonumber
$$
откуда следует, что существует предел eqref.
Из равенства eqref получаем
$$
f(x)-kx=b++alpha(x), где alpha(x)rightarrow 0 при xrightarrow+infty,nonumber
$$
откуда следует, что существует предел eqref.
Достаточность. Если существуют конечные пределы eqref и eqref, то (f(x)-(kx+b)=alpha(x)), где (alpha(x)rightarrow 0) при (xrightarrow+infty), то есть выполняется условие eqref. Это означает, что прямая (y=kx+b) — асимптота графика функции (y=f(x)) . (bullet)
Для случая горизонтальной асимптоты данная теорема формулируется в следующем виде: для того, чтобы прямая (y=b) была асимптотой графика функции (y=f(x)) при (xrightarrow+infty), необходимо и достаточно, чтобы (displaystyle lim_f(x)=b).
🌟 Видео
Асимптоты функции. 10 класс.Скачать

Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

Решение задач на вывод формул органических соединений | Химия 10 класс #8 | ИнфоурокСкачать

Математика без Ху!ни. Исследование функции, график. Первая, вторая производная, асимптоты.Скачать

Задание №35: вывод формулы органического соединения | Химия 10 класс | УмскулСкачать

Схема Горнера. 10 класс.Скачать

Пределы №6 Нахождение асимптот графиков функцийСкачать

Исследование точек разрыва функций. Графическое построение наклонных асимптот в MS ExcelСкачать

Исследование функции. Часть 4. Асимптоты графика функцииСкачать

Асимптоты функции. Практическая часть. 10 класс.Скачать

Задание 23 из ОГЭ Построение графиков функций с модулем | МатематикаСкачать

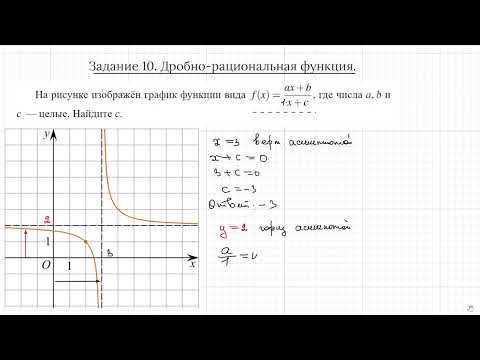
Задание 10. ЕГЭ профиль. Горизонтальные и вертикальные асимптоты гиперболы.Скачать
Математический анализ, 16 урок, Исследование функции и построение графикаСкачать

Нахождение асимптоты параметрически заданной функции.Скачать






