В общем случае нагрузка на стержень может быть задана интенсивностью сил с составляющими , и интенсивностью моментов с составляющими . Возможна также нагрузка, сосредоточенная в отдельных точках. Для бесконечно малой части стержня (рис.2.3) составим дифференциальные уравнения равновесия.
Из условий следуют уравнения:
Из условий получаем:
откуда, пренебрегая бесконечно малыми второго порядка, находим
Подставляя выражения в соответствующие дифференциальные уравнения, получаем
Интегрируя полученные шесть уравнений, находим выражения для внутренних усилий:
Постоянные интегрирования Сi (i=1,2. 6) определяются из граничных условий для рассматриваемых внутренних усилий.
Поскольку дифференциальные уравнения выражают равновесие любого бесконечно малого элемента стержня, то удовлетворение им означает выполнение условий равновесия стержня в целом.
Дифференциальные зависимости используются для проверки результатов, полученных с помощью алгебраических уравнений равновесия. Они позволяют, например, по эпюре определить характер эпюры . В частности, на участках, где =0 (=0), т.е. при соблюдении зависимостей
можно установить, что при Мz = const имеем Qy = 0(при Мy =const имеем Qz = 0). Переменная величина достигает экстремальных значений в точках, где Qy = 0(Qz = 0).
При определении внутренних усилий из уравнений равновесия целесообразно нагрузку на поверхности переносить в соответствующие точки на оси стержня с соблюдением условий статической эквивалентности. Полученная таким образом силовая схема является составной частью так называемой расчетной схемы (системы), когда брус представляется его осью.
Дата добавления: 2015-05-28 ; просмотров: 946 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Математика это не ИсламСкачать

Дифференциальные уравнения равновесия
Из тела, находящегося под действием внешних сил, вырежем мысленно в окрестности точки О элементарный параллелепипед, грани которого параллельны координатным плоскостям (рис. 4.5). Напряженное состояние в этой точке определяется напряжениями, которые показаны на невидимых гранях. Поскольку все напряжения являются функциями координат точек тела, то при переходе к параллельным граням они получат некоторые малые приращения. Обозначим с помощью штрихов величины напряжений на видимых гранях параллелепипеда.
При переходе на параллельные грани приращения обусловлены изменением только одной из координат. Например, для а’х справедливо равенство
Заменяя приближенно в этом выражении частное приращение частным дифференциалом, получим
Аналогично определяем и другие напряжения на видимых гранях.
Составим суммы проекций всех сил, действующих на параллелепипед, на оси координат. При этом учтем также действие объемных
сил. Обозначим отнесенные к единице объема тела проекции этих сил на оси координат через X, У, Z. Для вычисления равнодействующих объемных сил их нужно умножить на объем параллелепипеда.
Суммируя проекции всех сил на ось Ох и приравнивая их к нулю, получим
Входящие в это уравнение напряжения т‘ и x’xz определяются с помощью равенств, аналогичных (4.8) для напряжения о’:
Подставив эти равенства в (4.9), после приведения подобных членов и деления на dxdydz получим
Аналогично можно составить уравнения проекций всех сил на оси Оу и Oz. В итоге получим систему трех уравнений
которые называются дифференциальными уравнениями равновесия Навье.
Второе и третье уравнения равновесия могут быть также получены из первого путем так называемой круговой перестановки индексов, схематично показанной на рис. 4.6.
Дифференциальные уравнения равновесия устанавливают законы изменения напряжений при переходе от одной точки к бесконечно близко расположенной другой точке. С учетом закона парности касательных напряжений (4.4) эти уравнения содержат шесть неизвестных напряжений. Поскольку количество уравнений статики меньше количества неизвестных, то в общем случае задача определения напряжений является статически неопределимой.
Уравнения (4.10) могут быть также получены, если рассмотреть равновесие тела в целом. Составим уравнение суммы проекций всех сил на ось Ох, в которое войдут проекции объемных сил X и проекции поверхностной нагрузки р :
Здесь dV и dS — соответственно элементы объема и поверхности тела. Подставив во второй интеграл первое равенство (4.2), получим
Из курса высшей математики известна формула Гаусса—Остроградского, которая позволяет преобразовать интеграл по поверхности в интеграл по объему:
Используя эту формулу, запишем уравнение равновесия в виде
Поскольку это равенство справедливо при любых значениях dV, подынтегральное выражение должно быть равно нулю, что дает первое уравнение (4.10).
Видео:Асташова И. В. - Дифференциальные уравнения. Часть 2 - Фазовый портретСкачать

Дифференциальные уравнения равновесия
Рассмотрим равновесие элемента тела в форме параллелепипеда объемом dV. В этом случае напряжения на противоположных гранях будут отличаться на некоторую величину, определяемую путем разложения функции напряжения в ряд Тэйлора. В случае упругих (малых) деформаций тела можно ограничиться только линейными приращениями напряжений. На рис. 20.8 показаны положительные
Рис. 20.8. Напряжения, действующие вдоль оси х, в элементарном параллелепипеде напряжения на противоположных гранях элементарного параллелепипеда. Правило знаков:
Если нормаль к площадке совпадает с направлением оси координат, то положительное направление напряжения также совпадает с направлением соответствующей оси
Чтобы не загромождать чертеж, на нем обозначены только напряжения, проектирующиеся на ось*. Остальные компоненты напряжений показаны на рисунке стрелками без надписей. В этом разделе использована обычная система координат х, у, z, которая более привычна и наглядна, чем индексная система х,, х2, х3. Умение свободно переходить от одной системы координат к другой облегчает составление компьютерных программ.
Рассмотрим равновесие выделенного элемента. Спроектируем все силы на осьх:
ЗдесьрУх — проекция на осьх напряжения, вызванного объемными силами.
Разделив уравнение равновесия на объем элемента dV= dxdydz Эс Эх Эх
получаем ——ч—— + ——+pVr = 0 — первое из трех дифференци-
альных уравнений равновесия. По аналогии спроектировав все силы на оси у и z, получим еще два уравнения. В итоге получаем систему из трех дифференциальных уравнений равновесия (уравнения Навье):
Рассмотрев еще три уравнения равновесия суммы моментов всех сил относительно осей jc, у и z, получим уже известный из основного курса сопротивления материалов закон парности касательных напряжений: Ту = т;/ или тху = тух; тп = t.v = txz. Отсюда следует, что
📸 Видео
Дифференциальные уравнения для самых маленькихСкачать

Дифференциальные уравнения 2. Сопротивление воздухаСкачать

1. Что такое дифференциальное уравнение?Скачать

Дифференциальные уравнения. Задача Коши. Метод Эйлера.Скачать

#Дифуры II. Урок 5. Уравнение ЭйлераСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 1Скачать

Сопротивление материалов. Лекция: дифференциальное уравнение изогнутой оси балкиСкачать

2. Линейные уравнения с переменными коэффициентамиСкачать

Однородные дифференциальные уравнения первого порядкаСкачать
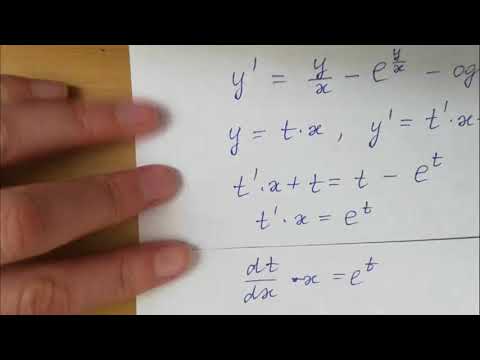
Откуда появляются дифференциальные уравнения и как их решатьСкачать

Дифференциальные уравнения при поперечном изгибе. ПРАВИЛЬНЫЙ СОПРОМАТ. Видео 1 Часть 1.Скачать

Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

Как решать диффуры?(Дифференциальные уравнения)Скачать

Дифференциальные уравнения, 8 урок, Линейные дифференциальные уравнения с const коэф-ами 2 порядкаСкачать

Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 2Скачать

Дифференциальное уравнение. Формула ЭйлераСкачать















