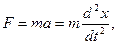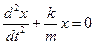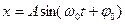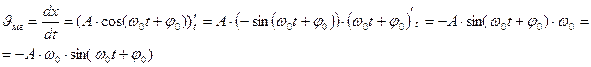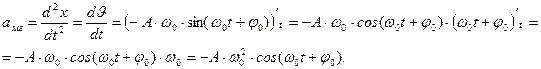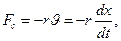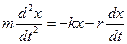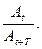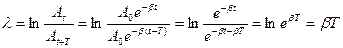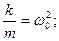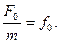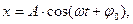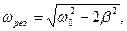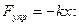Вывод дифференциального уравнения незатухающих колебаний (6 видео)

Уравнение свободных незатухающих гармонических колебаний.

Для возбуждения в контуре колебаний предварительно заряжают конденсатор, сообщая его обкладкам заряд ±q. Тогда в начальный момент времени t=0 (рис. 19, а) между обкладками конденсатора возникнет электрическое поле. Если замкнуть конденсатор на катушку индуктивности, конденсатор начнет разряжаться, и в контуре потечет возрастающий со временем ток I. Когда конденсатор полностью разрядится, энергия электрического поля конденсатора полностью перейдет в энергию магнитного поля катушки (рис. 19, б). Начиная с этого момента ток в контуре будет убывать, и, следовательно, начнет ослабевать магнитное поле катушки, тогда в ней согласно закону Фарадея индуцируется ток, который течет в соответствии с правилом Ленца в том же направлении, что и ток разрядки конденсатора. Конденсатор начнет перезаряжаться, возникнет электрическое поле, стремящееся ослабить ток, который, в конце концов, обратится в нуль, а заряд на обкладках конденсатора достигнет максимума (рис. 19, в). Далее те же процессы начнут протекать в обратном направлении (рис. 19, г), и система к моменту времени t=Т (Т – период колебаний) придет в первоначальное состояние (рис. 19, а). После этого начнется повторение рассмотренного цикла разрядки и зарядки конденсатора, то есть начнутся периодические незатухающие колебания величины заряда q на обкладках конденсатора, напряжения U_C на конденсаторе и силы тока I, текущего через катушку индуктивности. Согласно закону Фарадея напряжение U_C на конденсаторе определяется скоростью изменения силы тока в катушке индуктивности идеального контура, то есть :

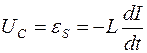
Исходя из того, что U_C=q/C, а I=dq/dt, получаем дифференциальное уравнение свободных незатухающих гармонических колебаний величины заряда q на обкладках конденсатора:

или .

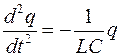
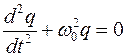
Решением этого дифференциального уравнения является функция q(t), то естьуравнение свободных незатухающих гармонических колебаний величины заряда q на обкладках конденсатора:

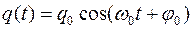
где q(t) – величина заряда на обкладках конденсатора в момент времени t;

q₀ – амплитуда колебаний заряда на обкладках конденсатора;

– круговая (или циклическая) частота колебаний ( ) ;

=2 /T (T – период колебаний, –формула Томсона);

– фаза колебаний в момент времени t;

– начальная фаза колебаний, то есть фаза колебаний в момент времени t=0.

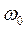
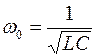
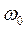
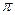
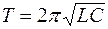
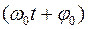
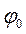
Уравнение свободных затухающих гармонических колебаний.В реальном колебательном контуре учитывается, что кроме катушки индуктивностью L, конденсатора емкостью С, в цепи также имеется резистор сопротивлением R,отличным от нуля, что является причиной затухания колебаний в реальном колебательном контуре. Свободные затухающие колебания – колебания, амплитуда которых из-за потерь энергии реальной колебательной системой с течением времени уменьшается.

Для цепи реального колебательного контура напряжения на последовательно включенных конденсаторе емкостью С и резисторе сопротивлением R складываются. Тогда с учетом закона Фарадея для цепи реального колебательного контура можно записать:

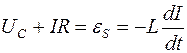
где 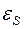– электродвижущая сила самоиндукции в катушке;

IR – напряжения на резисторе.

Исходя из того, что I=dq/dt, получаем дифференциальное уравнение свободных затухающих гармонических колебаний величины заряда q на обкладках конденсатора:

или ,

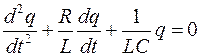
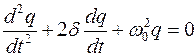
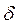
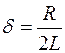
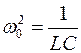
где – коэффициент затухания колебаний ( ) , .

Решением полученного дифференциального уравнения является функция q(t), то естьуравнение свободных затухающих гармонических колебаний величины заряда q на обкладках конденсатора:

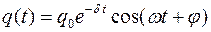
где q(t) – величина заряда на обкладках конденсатора в момент времени t;

– амплитуда затухающих колебаний заряда в момент времени t ;

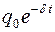
q₀ – начальная амплитуда затухающих колебаний заряда;

– круговая (или циклическая) частота колебаний ( );

– фаза затухающих колебаний в момент времени t;

– начальная фаза затухающих колебаний.

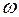
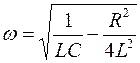
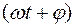
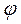
Период свободных затухающих колебаний в реальном колебательном контуре :

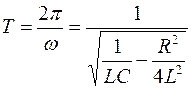
Вынужденные электромагнитные колебания. Чтобы в реальной колебательной системе получить незатухающие колебания, необходимо в процессе колебаний компенсировать потери энергии. Такая компенсация в реальном колебательном контуре возможна с помощью внешнего периодически изменяющегося по гармоническому закону переменного напряжения U(t):

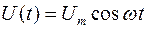
В этом случае дифференциальное уравнение вынужденных электромагнитных колебанийпримет вид:

или .

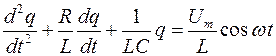
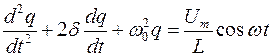
Решением полученного дифференциального уравнения является функция q(t):

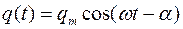
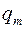
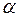
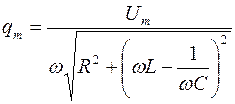
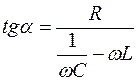
В установившемся режиме вынужденные колебания происходят с частотой w и являются гармоническими, а амплитуда и фаза колебаний определяются следующими выражениями:

; .

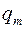
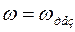
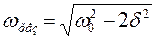
Отсюда следует, что амплитуда колебаний величины заряда имеет максимум при резонансной частоте внешнего источника :

Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающего переменного напряжения к частоте, близкой частоте 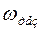, называется резонансом.

Тема 10. Электромагнитные волны

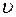
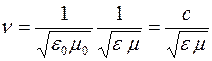
Согласно теории Максвелла электромагнитные поля могут существовать в виде электромагнитных волн, фазовая скорость распространения которых определяется выражением:

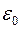
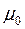
где и – соответственно электрическая и магнитная постоянные,

e и m – соответственно электрическая и магнитная проницаемости среды,

с – скорость света в вакууме ( ) .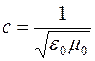

В вакууме (e = 1, m = l) скорость распространения электромагнитных волн совпадает со скоростью света( с ), что согласуется с теорией Максвелла о том,

что свет представляет собой электромагнитные волны.

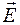
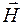
По теории Максвелла электромагнитные волны являются поперечными,то есть векторы и напряженностей электрического и магнитного полей взаимно перпендикулярны и лежат в плоскости, перпендикулярной вектору

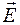
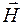
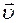
скорости распространения волны, причем векторы , и образуют правовинтовую систему (рис. 20).

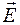
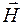
Из теории Максвелла следует также, что в электромагнитной волне векторы и колеблются в одинаковых фазах (рис. 20), то есть значения напряженностей Е и Н электрического и магнитного полей одновременно достигают максимума и одновременно обращаются в нуль, причем мгновенные значения Е и Н связаны соотношением: .

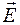
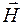
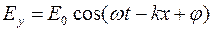
Уравнение плоской монохроматической электромагнитной волны (индексы у и z при Е и Н подчеркивают лишь то, что векторы и направлены вдоль взаимно перпендикулярных осей в соответствии с рис. 20):

где E₀ и Н₀– соответственно амплитуды напряженностей электрического и магнитного полей,

w – круговая частота волны, 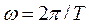(T – период колебаний),

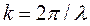
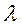
k – волновое число, ( – длина волны),

j – начальная фаза колебаний (начальная фаза колебаний j имеет одинаковое значение как для колебания электрического, так и магнитного векторов, так как в электромагнитной волне эти колебания происходят в одинаковых фазах).

Энергия электромагнитных волн. Электромагнитные волны переносят энергию. Объемная плотность w энергии электромагнитной волны складывается из объемных плотностей w_эл электрического и w_м магнитного полей:

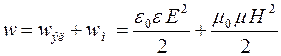
Учитывая выражение связи между величинами Е и Н , можно получить, что суммарная плотность энергии электрического и магнитного полей:

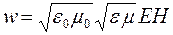
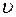
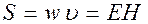
Умножив плотность энергии w на скорость распространения волны в среде, получим модуль плотности потока энергии:

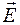
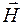
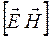
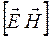
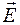
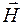
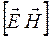
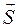
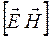
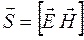
Tax как векторы и взаимно перпендикулярны, то произведение EH совпадает с модулем вектора ( – векторное произведение векторов и ). Кроме того, направление вектора совпадает с направлением распространения волны, то есть с направлением переноса энергии, что позволило ввести вектор ,равныйвекторному произведению , как вектор плотности потока электромагнитной энергии, называемыйвектором Умова–Пойнтинга:

Итак, вектор 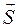направлен в сторону распространения электромагнитной волны, а его модуль равен энергии, переносимой электромагнитной волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны.

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Вывод дифференциального уравнения свободного колебания

На тело, совершающее свободные колебания, действуют две силы:

1. Сила, определяемая по второму закону Ньютона:

где m – масса тела;

а – ускорение;

х – смещение;

t – время.

2. Сила упругости, выраженная по закону Гука:

где k – коэффициент упругости. Знак минус показывает, что сила упругости F_упр всегда направлена в сторону положения равновесия.

На основании второго закона Ньютона (произведение массы тела на его ускорение равно сумме всех действующих сил) получаем:

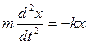
Перенесем –kx в левую часть равенства, получим:

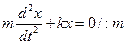
Введем замену: ,

где ω₀ – круговая (циклическая) частота колебаний (ω₀=2πν)

Получили дифференциальное уравнение второго порядка относительно смещения х.

Решением этого уравнения будет:

или (см. рис.1 и рис. 2).

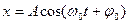
где А – амплитуда колебания;

φ₀ – начальная фаза;

ω₀t+φ₀ – фаза колебания в момент времени t;

ω₀t= ∆φ – изменение фазы колебания за время t.

Выведем уравнения мгновенной скорости и мгновенного ускорения, если колебания совершаются по закону косинуса.

Затухающие колебания.

Все реальные гармонические колебания происходят при воздействии сил сопротивления, на преодоление которых тело затрачивает часть своей энергии, в результате амплитуда колебания уменьшается со временем, т.е. колебания носят затухающий характер.

Представим график затухающего колебания:

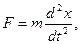
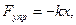
Вывод дифференциального уравнения затухающего колебания.На тело, кроме силы силы упругости действует сила сопротивления:

где r – коэффициент сопротивления.

Согласно второму закону Ньютона можно записать:

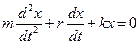
Разделим на массу m, получим:

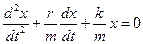
Введем обозначения: ,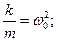

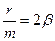
где β – коэффициент затухания.

Получили дифференциальное уравнение затухающего колебания:

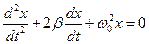
Решение уравнения существенно зависит от знака разности ,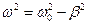

где ω— круговая частота затухающих колебаний, ω₀ — круговая частота собственных колебаний системы (без затухания).

При ω>0 решение дифференциального уравнения будет следующим:

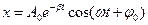
Амплитуда затухающего колебания в любой момент времени t определяется равенством:

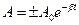
где А₀ – начальная амплитуда, указанная на графике (см. рис 3).

Период Т затухающих колебаний определяется по формуле:

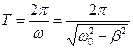
Скорость затухания (быстрота уменьшения амплитуды) определяется величиной коэффициента затухания β: чем больше β, тем быстрее уменьшается амплитуда.

Для характеристики скорости затухания ввели понятие декремента затухания.

Декрементом затухания называется отношение двух соседних амплитуд, разделенных периодом:

На практике степень затухания характеризуется логарифмическим декрементомзатухания λ, равным:

Выведем формулу, связывающую логарифмический декремент затухания λ с коэффициентом затухания β и периодом колебания Т.

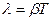
Выведем размерность коэффициента затухания

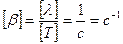
Вынужденные колебания. Вынужденными колебанияминазываются колебания, возникающие в системе при воздействии на неё внешней силы, изменяющейся по периодическому закону.

Пусть на систему действует сила:

где F₀ – максимальное значение,

ω — круговая частота колебаний внешней силы.

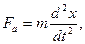
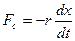
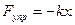
На систему действуют сила сила сопротивления и сила упругости .

С учетом всех четырех сил на основании второго закона Ньютона запишем:

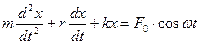
Разделим обе части равенства на m, получим:

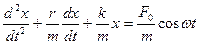
Получили дифференциальное уравнение вынужденного колебания:

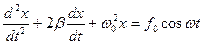
Представим график вынужденных колебаний:

Вывод дифференциального уравнения незатухающих колебаний

В начале амплитуда колебаний возрастает, а затем становится постоянной А.

Для установившихся вынужденных колебаний:

(см. рис. 4)

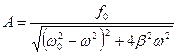
Резонанс.Если ω₀ и β для системы заданы, то амплитуда А вынужденных колебаний имеет максимальное значение при некоторой определенной частоте вынуждающей силы, называемой резонансной. Достижение максимальной амплитуды вынужденных колебаний для заданных ω₀ и β называется резонансом.

Резонансная круговая частота определяется формулой:

а резонансная амплитуда:

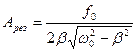
Если отсутствует сопротивление (β=0), то амплитуда неограниченно возрастает.

Представим на графиках зависимость амплитуды вынужденных колебаний от круговой частоты вынуждающей силы ω при различных значениях коэффициента затухания:

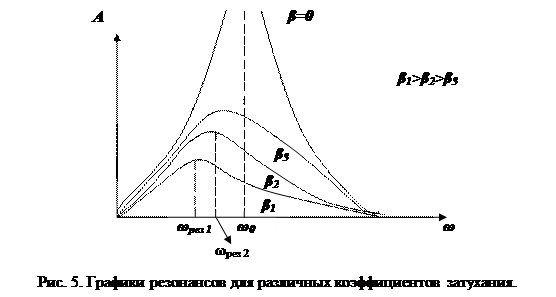По виду резонансной кривой резонанс может быть острым при β→0, тупым – при β→1. (см. рис. 5).

По механизму возбуждения резонанс классифицируется на:

— механический; акустический; электромагнитный; парамагнитный; ядерномагнитный.

Возникновение резонансных явлений в организме может быть как полезным, так и вредным. Например, на акустическом резонансе основано восприятия звука, инфразвук может вызвать разрыв тканей внутренних органов.

Автоколебания.При затухающих колебаниях энергия системы расходуется на преодоление сопротивления среды. Если восполнять эту потерю энергии, то колебания станут незатухающими. Пополнять эту потерянную системой энергию можно за счет источника энергии извне, а можно сделать так, чтобы колеблющаяся система сама бы управляла внешним воздействием.

Незатухающие колебания, возникающие в системе за счет источника энергии, не обладающего колебательными свойствами, называются автоколебаниями, а сами системы – автоколебательными.

Классическим примером автоколебаний являются часы: заведенная пружина; поднятая гиря – источник энергии; анкер – регулятор поступления энергии от источника; маятник или баланс – колебательная система.

Амплитуда и частота автоколебаний зависят от свойств самой автоколебательной системы.

Автоколебания осуществляется по следующей схеме:

Через канал обратной связи регулятор, получив информацию о состоянии колебательной системы, осуществляет регулирующую подачи энергии от источника к системе.

К автоколебательным системам относятся сердце, легкие и т.д.

Автоколебательная система сердца может быть представлена в следующем виде:

Порядок выполнения работы:

Включить кимограф, записать положение равновесия.
Отклонив маятник в сторону, отпустить его, одновременно включив секундомер.
После записи последнего n-го колебания отключить секундомер.
После последнего колебания зарегистрировать положение равновесия и отключить кимограф.
Записать графики 3-го – 5-го колебательных процессов.
С помощью линейки для каждого графика определить величину начальной амплитуды (А₀) и последней амплитуды (А_n).
Подсчитать число полных колебаний на графике (n).
Определить период колебания T:

где t – время по секундомеру.

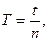
Определить величину коэффициента затухания по формуле:

Определить величину логарифмического декремента затухания: .
Полученные данные занести в таблицу.

п/п

А₀ (см)

А_n (см)

t(c)

T(c)

β(c -1 )

Контрольные вопросы

Определения и единицы измерения основных характеристик колебательного движения.
Гармонические колебания. Вывод дифференциального уравнения гармонического колебания и его решение.
Затухающие колебания. Вывод дифференциального уравнения затухающего колебания и его решение.
Декремент затухания, логарифмический декремент затухания. Вывод формулы, связывающей логарифмический декремент с периодом колебания и коэффициентом затухания.
Вынужденные колебания. Дифференциальное уравнение вынужденного колебания и его решение.
Резонанс и его значение в медицине.
Автоколебания.

Тестовые задания

Циклической (круговой) частотой называется число полных колебаний за:

а) 1 с; б) 1 мин; в) 1 ч; г) 2π с.

Укажите формулу, связывающую циклическую частоту ω с частотой ν:

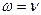
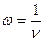
а) ; в) ;

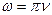
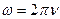
б) ; г) .

Укажите формулу, по которой определяется амплитуда затухающего колебания в любой момент времени t:

а) 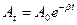; в) ;

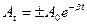
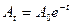
б) . г) .

Декрементом затухания называется отношение:

а) двух соседних амплитуд;

б) двух соседних амплитуд, разделенных периодом;

в) первой и последней амплитуд;

г) двух амплитуд, разделенных полупериодом.

Укажите единицу измерения коэффициента затухания β:

б) безразмерная величина; г) .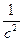

6. Укажите решение дифференциального уравнения свободного гармонического колебания:

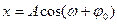
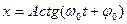
а) ; в) ;

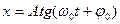
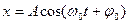
б) ; г) .

7. Укажите, сколько сил действует на систему, если она совершает свободные гармонические колебания:

8. Укажите дифференциальное уравнение свободного гармонического колебания:

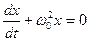
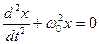
а) ; в) ;

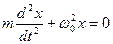
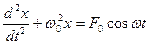
б) ; г) .

9. Укажите решение дифференциального уравнения затухающего колебания:

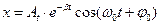
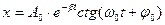
а) ; в) ;

б) 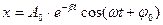; г) .

10. Сколько полных колебаний тело должно совершить в одну минуту, чтобы частота его колебаний равнялась 1 Гц:

11. Укажите подстановку в уравнение смещения затухающего колебания:

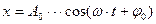
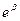
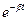
а) ; в) ;

б) ; г) ;

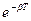
12. Укажите, сколько сил действует на систему, если она совершает вынужденные колебания:

13. Укажите дифференциальное уравнение вынужденного колебания:

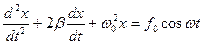
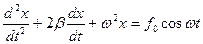
а) ; в) ;

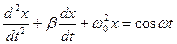
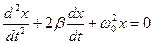
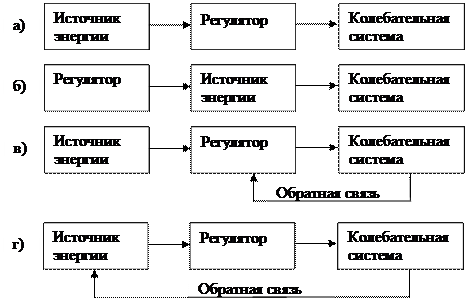
б) ; г) .

14. Укажите блок – схему, по которой осуществляются автоколебания:

15. Укажите формулу, связывающую логарифмический декремент затухания λ с периодом колебания Т и коэффициентом затухания β:

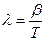
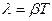
а) ; в) ;

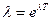
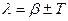
б) ; г) .

16. Укажите дифференциальное уравнение затухающего колебания:

а) ; в) ;

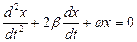
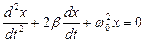
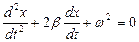
б) ; г) .

17. Укажите, по какой формуле определяется период колебания Т, если за время t тело совершило n полных колебаний:

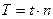
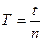
а) ; в) ;

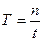
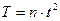
б) ; г) .

18. Укажите единицу измерения логарифмического декремента затухания:

б) с 2 ; г) безразмерная величина.

19. Укажите, какой параметр в уравнении смещения указывает на то, что процесс носит затухающий характер:

20. Укажите, какая сила вызывает уменьшение амплитуды при затухающих колебаниях:

а) ускоряющая сила;

б) сила упругости;

в) сила сопротивления;

г) сила давления.

21. Укажите, при каком значении декремента затухания процесс затухания будет проходить наиболее медленно:

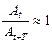
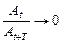
а) ; в) ;

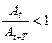
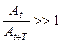
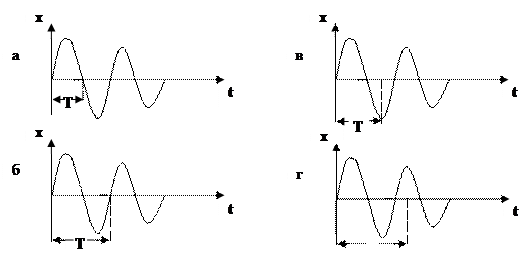
б) ; г) .

22. Укажите, на каком из графиков показан период колебания Т:

23. Укажите график вынужденного колебания:

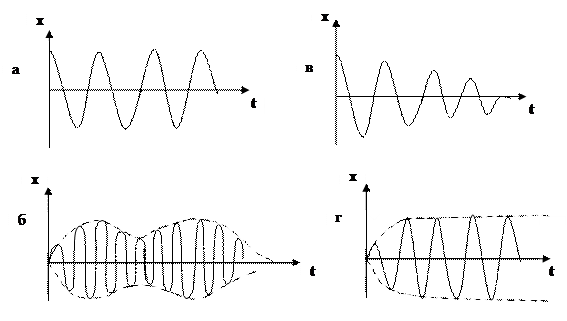24. Укажите, каков физический смысл знака «-» в формуле закона Гука

а) физический смысл отсутствует;

б) показывает, что направления силы упругости F_упр и смещения х совпадают;

в) показывает, что направления силы упругости F_упр и смещения х противоположны;

г) показывает, что направления силы упругости F_упр и смещения х взаимно перпендикулярны.

25. Частотой колебания ν называется величина, показывающая число полных колебаний:

а) за минуту; в) за час;

б) за секунду; г) за сутки.

26. Укажите, в каких единицах измеряется циклическая частота ω:

а) в секундах; в) в минутах;

б) в Гц ; г) в часах.

27. Укажите условие резонанса при β=0:

Видео:Урок 343. Затухающие колебания (часть 1)Скачать

Свободные колебания пружинного маятника. Общие сведения

Цель работы. Ознакомиться с основными характеристиками незатухающих и затухающих свободных механических колебаний.

Задача. Определить период собственных колебаний пружинного маятника; проверить линейность зависимости квадрата периода от массы; определить жесткость пружины; определить период затухающих колебаний и логарифмический декремент затухания пружинного маятника.

Приборы и принадлежности. Штатив со шкалой, пружина, набор грузов различной массы, сосуд с водой, секундомер.

1. Свободные колебания пружинного маятника. Общие сведения

Колебаниями называются процессы, в которых периодически изменяется одна или несколько физических величин, описывающих эти процессы. Колебания могут быть описаны различными периодическими функциями времени. Простейшими колебаниями являются гармонические колебания – такие колебания, при которых колеблющаяся величина (например, смещение груза на пружине) изменяется со временем по закону косинуса или синуса. Колебания, возникающие после действия на систему внешней кратковременной силы, называются свободными.

Рассмотрим одну из простейших колебательных систем – пружинный маятник, представляющий собой груз массой m, подвешенный на абсолютно упругой пружине с коэффициентом жесткости k
(рис. 1). Пусть l0 – длина пружины без подвешенного к ней груза. При подвешивании груза под действием силы тяжести пружина растянется на x1 так, что маятник будет находиться в положении равновесия вследствие равенства модулей силы тяжести mg и упругой силы Fупр: mg = kx1, стремящейся вернуть груз в положение равновесия (полагается, что деформации пружины идеально упругие и подчиняются закону Гука).

Если груз вывести из положения равновесия, отклонив на величину x, то сила упругости возрастает: Fупр = – kx2= – k(x1 + x). Дойдя до положения равновесия, груз будет обладать отличной от нуля скоростью и пройдет положение равновесия по инерции. По мере дальнейшего движения будет увеличиваться отклонение от положения равновесия, что приведет к возрастанию силы упругости, и процесс повторится в обратном направлении. Таким образом, колебательное движение системы обусловлено двумя причинами: 1) стремлением тела вернуться в положении равновесия и 2) инерцией, не позволяющей телу мгновенно остановиться в положении равновесия. В отсутствии сил трения колебания продолжались бы сколь угодно долго. Наличие силы трения приводит к тому, что часть энергии колебаний переходит во внутреннюю энергию и колебания постепенно затухают. Такие колебания называются затухающими.

Незатухающие свободные колебания

Сначала рассмотрим колебания пружинного маятника, на который не действуют силы трения – незатухающие свободные колебания. Согласно второму закону Ньютона c учетом знаков проекций на ось X

(1)

Из условия равновесия смещение, вызываемое силой тяжести: . Подставляя в уравнение (1), получим: . Разделив правую и левую часть этого уравнения на m и принимая, что a = d2x/dt2, получим дифференциальное уравнение

. (2)

Это уравнение называется дифференциальным уравнением гармонических колебаний пружинного маятника. Из этого уравнения следует, что после прекращения внешнего воздействия, приводящего к первоначальному отклонению системы от положения равновесия, движение груза обусловлено только действием упругой силы (сила тяжести вызывает постоянное смещение).

Общее решение однородного дифференциального уравнения второго порядка (2) имеет вид

. (3)

Данное уравнение называется уравнением гармонических колебаний. Наибольшее отклонение груза от положения равновесия А0 называется амплитудой колебаний. Величина , стоящая в аргументе косинуса, называется фазой колебания. Постоянная φ0 представляет собой значение фазы в начальный момент времени (t = 0) и называется начальной фазой колебаний. Величина

(4)

есть круговая или циклическая частота собственных колебаний, связанная с периодом колебаний Т соотношением . Период колебаний определяется

. (5)

Рассмотрим свободные колебания пружинного маятника при наличии силы трения (затухающие колебания). В простейшем и вместе с тем наиболее часто встречающемся случае сила трения пропорциональна скорости υ движения:

где r – постоянная, называемая коэффициентом сопротивления. Знак минус показывает, что сила трения и скорость имеют противоположные направления. Уравнение второго закона Ньютона в проекции на ось Х при наличии упругой силы и силы трения

Данное дифференциальное уравнение с учетом υ = dx/dt можно записать

, (8)

где – коэффициент затухания; – циклическая частота свободных незатухающих колебаний данной колебательной системы, т. е. при отсутствии потерь энергии (β = 0). Уравнение (8) называют дифференциальным уравнением затухающих колебаний.

Чтобы получить зависимость смещения x от времени t, необходимо решить дифференциальное уравнение (8). В случае малых затуханий () решение уравнения можно записать следующим образом:

, (9)

где А0 и φ0 – начальная амплитуда и начальная фаза колебаний;
– циклическая частота затухающих колебаний при ω >> ω ≈ ω0.

Движение груза в этом случае можно рассматривать как гармоническое колебание с частотой ω и переменной амплитудой, меняющейся по закону:

. (10)

На графике функции (9), рис. 2, пунктирными линиями показано изменение амплитуды (10) затухающих колебаний.

Рис. 2. Зависимость смещения х груза от времени t при наличии силы трения

Для количественной характеристики степени затухания колебаний вводят величину, равную отношению амплитуд, отличающихся на период, и называемую декрементом затухания:

. (11)

Часто используют натуральный логарифм этой величины. Такой параметр называется логарифмическим декрементом затухания:

. (12)

Если за время t‘ амплитуда уменьшается в n раз, то из уравнения (10) следует, что

. (13)

Отсюда для логарифмического декремента получаем выражение

. (14)

Если за время t‘ амплитуда уменьшается в е раз (е = 2,71 – основание натурального логарифма), то система успеет совершить число колебаний

. (15)

Следовательно, логарифмический декремент затухания – величина, обратная числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в е раз. Чем больше θ, тем быстрее происходит затухание колебаний.

2. Методика эксперимента и экспериментальная установка

Рис. 3. Схема установки

Установка состоит из штатива 1 с измерительной шкалой 2. К штативу на пружине 3 подвешиваются грузы 4 различной массы. При изучении затухающих колебаний в задании 2 для усиления затухания используется кольцо 5, которое помещается в прозрачный сосуд 6 с водой.

В задании 1 (выполняется без сосуда с водой и кольца) в первом приближении затуханием колебаний можно пренебречь и считать гармоническими. Как следует из формулы (5) для гармонических колебаний зависимость T 2 = f (m) – линейная, из которой можно определить коэффициент жесткости пружины k по формуле

, (16)

где – угловой коэффициент наклона прямой T 2 от m.

Задание 1. Определение зависимости периода собственных колебаний пружинного маятника от массы груза.

1. Определить период колебаний пружинного маятника при различных значениях массы груза m. Для этого с помощью секундомера для каждого значения m трижды измерить время t полных n колебаний (n ≥10) и по среднему значению времени вычислить период . Результаты занести в табл. 1.

2. По результатам измерений построить график зависимости квадрата периода T2 от массы m. Из углового коэффициента графика определить жесткость пружины k по формуле (16).

Результаты измерений для определения периода собственных колебаний

, с