В этом разделе мы покажем, что уравнения колебательного движения многих систем, в сущности, одинаковы, так что различные физические процессы могут быть описаны одними и теми же математическими формулами.
Пружинный маятник — это система, состоящая из шарика массой m, подвешенного на пружине длиной 
Рис. 1.2. К выводу уравнения движения для пружинного маятника
В положении равновесия (рис. 1.2) сила тяжести 

где 
Если теперь оттянуть шарик от положения равновесия на расстояние x, то полное удлинение пружины станет равным 
Знак минус означает, что сила стремится уменьшить отклонение от положения равновесия. Полученное выражение соответствует упругой силе слабо деформированной пружины.
Запишем теперь уравнение второго закона Ньютона:
Его можно также представить в виде:
Математический маятник
Математический маятник — это идеализированная система, состоящая из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке.
Будем характеризовать отклонение маятника от положения равновесия углом 
Рис. 1.3. К выводу уравнения движения математического маятника
При отклонении маятника от положения равновесия на материальную точку массой m действуют сила тяжести 


Проецируя его на направления нормали и касательной к траектории (окружности радиуса 
Модуль скорости 




Тогда второе из написанных выше уравнений движения приобретает вид
При малых отклонениях маятника от вертикали, когда 
Физический маятник
Физический маятник — это протяженное колеблющееся тело, закрепленное на оси. Его размеры таковы, что его невозможно рассматривать как материальную точку.
Пример физического маятника приведен на рис. 1.4.
Рис. 1.4. К выводу уравнения движения физического маятника
При отклонении маятника от положения равновесия на угол 
где m – масса маятника, а l – расстояние 0C между точкой подвеса 0 и центром масс C маятника.
Рассматривая 




Ограничимся рассмотрением малых отклонений от положения равновесия:
В этом случае уравнение колебаний принимает вид:
В случае, когда физический маятник можно представить как материальную точку, колеблющуюся на нити длиной l, момент инерции равен
и мы приходим к уравнению (1.6) движения математического маятника.
Колебания поршня в сосуде с идеальным газом
Рассмотрим цилиндр с площадью поперечного сечения 




Рис. 1.5. Колебания поршня, закрывающего сосуд с идеальным газом
В состоянии равновесия давление в газе под поршнем складывается из атмосферного давления 


Переместим поршень на расстояние x вверх. Объем сосуда увеличится и станет равным
Соответственно уменьшится давление. В силу предположения об отсутствии теплообмена, новое давление в газе можно найти из уравнения адиабаты Пуассона
Здесь 
При малых колебаниях, когда изменение объема газа 

выражение (1.11) можно разложить в ряд Тейлора:
На поршень действуют три силы: сила атмосферного давления 



Используя (1.13), уравнение движения поршня
- Уравнение колебаний маятника
- Изучение колебаний физического маятника, методические указания к лабораторной работе № 3
- Методические указания
- Волгоград 2010
- где М – момент внешних сил;
- — угловое ускорение движения маятника, которое характеризует быстроту изменения угловой скорости по времени, и равно второй производной от угла поворота по времени;
- J – момент инерции тела относительно оси вращения О.
- Момент инерции маятника выразим, используя теорему Штейнера. Согласно данной теореме момент инерции твердого тела J относительно произвольной оси складывается из момента инерции Jс относительно параллельной оси, проходящей через центр инерции, и произведения массы тела на квадрат расстояния между осями
- Момент внешних сил М складывается из момента силы тяжести и момента сил трения, которым в нашем рассмотрении можно пренебречь, т. е. считать, что Мтр=0. Момент силы тяжести равен произведению силы тяжести mg на расстояние от линии действия силы до оси вращения l sina (плечо силы, рис.1)
- (4)
- Решение этого уравнения можно записать в виде
- 📺 Видео
Видео:Механика. Л 10.1. Колебания. Вывод дифференциального уравнения пружинного маятникаСкачать

Уравнение колебаний маятника
Рис.1
Исследуем выражение (2) в зависимости от разности фаз (φ2 — φ1):
1) φ2 — φ1 = ±2mπ (m = 0, 1, 2, . ), тогда A=A1+A2, т. е. амплитуда результирующего колебания А будет равна сумме амплитуд складываемых колебаний;
2) φ2 — φ1 = ±(2m+1)π (m = 0, 1, 2, . ), тогда A=|A1–A2|, т. е. амплитуда результирующего колебания будет равна разности амплитуд складываемых колебаний.
Для практики представляет особый интерес случай, когда два складываемых гармонических колебания одинакового направления мало отличаются по частоте. После сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой. Периодические изменения амплитуды колебания, которые возникают при сложении двух гармонических колебаний с близкими частотами, называются биениями.
Пусть амплитуды складываемых колебаний равны А, а частоты равны ω и ω+Δω, причем Δω
23 Колебания физического маятника.
Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.
Определения
— угол отклонения маятника от равновесия;
— начальный угол отклонения маятника;
— масса маятника;
— расстояние от точки подвеса до центра тяжести маятника;
— радиус инерции относительно оси, проходящей через центр тяжести.
— ускорение свободного падения.
Момент инерции относительно оси, проходящей через точку подвеса:

[править] Дифференциальное уравнение движения физического маятника
Основная статья: Приведённая длина
Пренебрегая сопротивлением среды, дифференциальное уравнение колебаний физического маятника в поле силы тяжести записывается следующим образом:
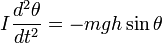
Полагая 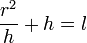
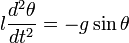
Последнее уравнение аналогично уравнению колебаний математического маятника длиной 

[править] Центр качания физического маятника
Центр качания — точка, в которой надо сосредоточить всю массу физического маятника, чтобы его период колебаний не изменился.
Поместим на луче, проходящем от точки подвеса через центр тяжести точку на расстоянии 
Действительно, если всю массу сосредоточить в центре качания, то центр качания будет совпадать с центром масс. Тогда момент инерции относительно оси подвеса будет равен 
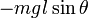
[править] Теорема Гюйгенса
[править] Формулировка
Если физический маятник подвесить за центр качания, то его период колебаний не изменится, а прежняя точка подвеса сделается новым центром качания.
[править] Доказательство
Вычислим приведенную длину для нового маятника:
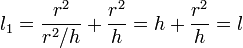
Совпадение приведённых длин для двух случаев и доказывает утверждение, сделанное в теореме.
[править] Период колебаний физического маятника
Для того, чтобы найти период колебаний физического маятника, необходимо решить уравнение качания. Для этого умножим левую часть этого уравнения на 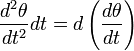
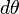
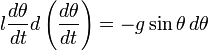
Интегрируя это уравнение, получаем.
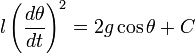
где 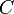
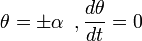
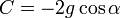
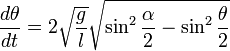
Отделяем переменные и интегрируем это уравнение:
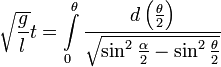
Удобно сделать замену переменной, полагая 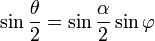
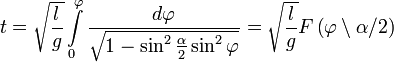
Здесь 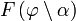
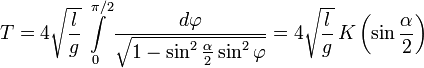
Здесь 
[править] Период малых колебаний физического маятника
Если амплитуда колебаний 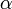
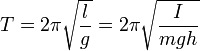
24 Колебания математического маятника
Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебаний математического маятника длины l неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен
и не зависит [1] от амплитуды и массы маятника.
Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы.
При малых колебаниях физический маятник колеблется так же, как математический с приведённой длиной.
Уравнение колебаний маятника
Колебания математического маятника описываются обыкновенным дифференциальным уравнением вида
где ω ― положительная константа, определяемая исключительно из параметров маятника. Неизвестная функция x(t) ― это угол отклонения маятника в момент t от нижнего положения равновесия, выраженный в радианах; 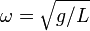
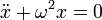
[править] Решения уравнения движения
[править] Гармонические колебания
Маятник, совершающий малые колебания, движется по синусоиде. Поскольку уравнение движения является обыкновенным ДУ второго порядка, для определения закона движения маятника необходимо задать два начальных условия — координату и скорость, из которых определяются две независимых константы:
где A — амплитуда колебаний маятника, θ0 — начальная фаза колебаний, ω — циклическая частота, которая определяется из уравнения движения. Движение, совершаемое маятником, называется гармоническими колебаниями
[править] Нелинейный маятник
Для маятника, совершающего колебания с большой амплитудой, закон движения более сложен:
где 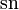

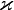
Параметр 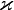
где 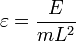
Период колебаний нелинейного маятника
где K — эллиптический интеграл первого рода.
[править] Движение по сепаратрисе
Движение маятника по сепаратрисе является непериодическим. В бесконечно далёкий момент времени он начинает падать из крайнего верхнего положения в какую-то сторону с нулевой скоростью, постепенно набирает её, и останавливается, возвратившись в исходное положение.
25 Затухающие колебания. Зависимость амплитуды от времени.
Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс вида 
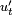
Пускай имеется система, состоящая из пружины (подчиняющейся закону Гука), один конец которой жёстко закреплён, а на другом находится тело массой m. Колебания совершаются в среде, где сила сопротивления пропорциональна скорости с коэффициентом c (см. вязкое трение).
Тогда второй закон Ньютона для рассматриваемой системы запишется так:
где Fc — сила сопротивления, Fy — сила упругости
или в дифференциальной форме
где k — коэффициент упругости в законе Гука, c — коэффициент сопротивления, устанавливающий соотношение между скоростью движения грузика и возникающей при этом силой сопротивления.
Для упрощения вводятся следующие обозначения:
Величину ω называют собственной частотой системы, ζ — коэффициентом затухания.
Тогда дифференциальное уравнение принимает вид
Сделав замену x = e λt , получают характеристическое уравнение
Корни которого вычисляются по следующей формуле
[править] Решения
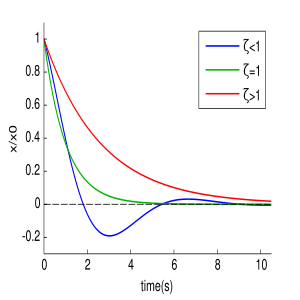
Зависимость графиков колебаний от значения ζ.
В зависимости от величины коэффициента затухания решение разделяется на три возможных варианта.
Если 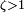
В этом случае колебания с самого начала экспоненциально затухают.
- Граница апериодичности
Если 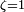
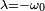
В данном случае может иметь место вре́менный рост, но потом — экспоненциальное затухание.
Если 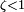
Тогда решением исходного дифференциального уравнения является
Где 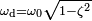
Константы c1 и c2 в каждом из случаев определяются из начальных условий:
26 Вынужденные колебания. Понятие резонанса.
Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.
Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.
Наиболее простой и содержательный пример вынужденных колебаний можно получить из рассмотрения гармонического осциллятора и вынуждающей силы, которая изменяется по закону: 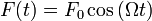
Видео:Математический маятник или откуда формула периодаСкачать

Изучение колебаний физического маятника, методические указания к лабораторной работе № 3
На правах рукописи
Министерство образования Российской Федерации
Волгоградская государственная архитектурно-строительная академия
ИЗУЧЕНИЕ КОЛЕБАНИЙ ФИЗИЧЕСКОГО МАЯТНИКА
Видео:9. Колебания физического маятникаСкачать

Методические указания
Видео:Классические уравнения | математический маятник | вывод через второй закон НьютонаСкачать

Волгоград 2010
Методические указания к лабораторной работе № 3 по курсу физики «Изучение колебаний физического маятника» / Сост. ; ВолгГАСА.—Волгоград, 2002. – 8 с.
Для студентов всех специальностей.
Табл. 3. Библиогр. 3 назв.
© Волгоградская государственная архитектурно-строительная академия, 2002
Цель работы: Исследование зависимости периода колебаний физического маятника от его длины, определение момента инерции маятника и ускорения свободного падения.
Приборы и принадлежности: физический маятник в виде металлической линейки с отверстиями, секундомер.

Пусть маятник массой m и длиной l отклонен от положения равновесия на угол a. Движение физического маятника описывается основным законом динамики вращательного движения, который для абсолютно твердого тела имеет вид
Видео:Математические и пружинные маятники. 11 класс.Скачать

 где М – момент внешних сил;
где М – момент внешних сил;
Видео:физический маятникСкачать

— угловое ускорение движения маятника, которое характеризует быстроту изменения угловой скорости по времени, и равно второй производной от угла поворота по времени;
Видео:Физический маятникСкачать

J – момент инерции тела относительно оси вращения О.
Видео:ЛР 1.05 Изучение колебаний физического маятникаСкачать

Момент инерции маятника выразим, используя теорему Штейнера. Согласно данной теореме момент инерции твердого тела J относительно произвольной оси складывается из момента инерции Jс относительно параллельной оси, проходящей через центр инерции, и произведения массы тела на квадрат расстояния между осями
В нашем случае Jс – момент инерции относитльно оси, проходящей параллельно оси вращения через центр тяжести маятника С.
Видео:Классические уравнения | физический маятник | вывод при помощи уравнения Эйлера - ЛагранжаСкачать

Момент внешних сил М складывается из момента силы тяжести и момента сил трения, которым в нашем рассмотрении можно пренебречь, т. е. считать, что Мтр=0. Момент силы тяжести равен произведению силы тяжести mg на расстояние от линии действия силы до оси вращения l sina (плечо силы, рис.1)
Знак минус показывает, что момент силы направлен противоположно углу отклонения маятника от положения равновесия, т. е является возвращающим моментом. Подставив (3) в (1), получим
Это уравнение, справедливое для любых значений амплитуды колебаний физического маятника, можно упростить для случая малых колебаний, когда угол отклонения маятника от положения равновесия мал и можно положить sina»a. Тогда уравнение движения маятника принимает вид
Видео:Теормех. 2021-окт-18. Группа ПМФ. Двойной маятникСкачать

 (4)
(4)
Видео:Колебания математического маятникаСкачать

Решение этого уравнения можно записать в виде
где ao – амплитуда колебаний (максимальное отклонение);
wo – собственная частота колебаний;
jo — начальная фаза колебаний.
Продифференцировав дважды уравнение (5) по времени и подставив в дифференциальное уравнение (4), получим соотношение
которое удовлетворяется при условии Jwo2- mgl=0. Отсюда собственная частота колебаний физического маятника
Тогда уравнение движения можно записать в виде дифференциального уравнения свободных гармонических колебаний

Амплитуда и начальная фаза колебаний определяются из начальных условий. Если в начальный момент времени t=0 известны угол отклонения маятника от положения равновесия a(0) и угловая скорость движения маятника da/dt=w(0) (не путать угловую скорость движения маятника w с собственной частотой колебаний wо!), имеем
a(0)=aosinjo и w(0)=woaocosjo.
Решая эту систему уравнений, получаем ao=(a2(0)+w2(0)/wo2)1/2 и jo=arctg(woa(0)/w(0)). Отсюда находим, что, если в начальный момент времени маятник покоится w(0)=0 в положении a=a(0), то амплитуда равна начальному отклонению маятника aо=a(0), а начальная фаза jо=p/2. Решение дифференциального уравнения для таких начальных условий имеет вид a(t)=ao sin (wot+p/2).

Если размеры тела малы по сравнению с длиной маятника l, то есть тело можно принять за материальную точку, подвешенную на невесомой нерастяжимой нити, то такой маятник является математическим маятником с периодом
Здесь учли, что момент инерции материальной точки относительно оси J=ml2. Как видим из сравнения (8) и (9), в отличие от математического маятника, период колебаний которого зависит только от длины и ускорения свободного падения, период колебаний физического маятника зависит также от его массы и момента инерции. Каждому физическому маятнику можно подобрать такой математический маятник, период колебаний которого равен периоду колебаний физического маятника. Длина такого математического маятника называется приведенной длиной физического маятника. Сопоставив (8) и (9) получим выражение для приведенной длины физического маятника
В отличие от математического маятника, зависимость периода колебаний которого от длины T
l1/2, для физического маятника, зависимость T(l) более сложная и представлена на рис.2.
Рис. 2. Зависимость периода колебаний физического маятника от длины.
Как следует из формулы (9), при l ® 0 период физического маятника
Т® ∞, то есть, если ось вращения проходит через центр инерции, то маятник находится в состоянии безразличного равновесия. При увеличении l ( когда выполняется условие ml2 >> Jc) период колебаний физического маятника стремится к периоду колебаний математического маятника. Зависимость Т(l) имеет минимум при некотором значении lmin.
Измеряя зависимость T(l) и построив график, можно определить момент инерции физического маятника Jc и ускорение свободного падения g. Для этого при Тмат> Т>Тmin находим два значения li и lk , соответствующие одному и тому же периоду Тi=Tk=T (рис. 2). Применив формулу (8) можно
записать
Решая совместно систему уравнений (11) и (12) относительно величин Jc и g , получим
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Подвесить физический маятник на седлообразную выемку опорной призмы отверстием, отстоящим от центра масс на величину l (см. табл. 3). Отклонить маятник на небольшой угол и отпустить. Измерить время 25 полных колебаний t¢. После этого подвесить маятник за симметричное отверстие, расположенное на таком же расстоянии от центра масс, и повторить измерение времени t¢¢. Найти среднее значение tср=(t¢+t¢¢)/2 и вычислить период колебаний T=tср/25. Результаты измерений занести в таблицу 1.
📺 Видео
математический маятник ЕГЭ ФИЗИКА колебания частота периодСкачать

Колебания. Физический маятник. Период и частота колебаний физического маятника.Скачать

Физический маятникСкачать

Колебания математического и пружинного маятников. 9 класс.Скачать

Физический маятник.Скачать

Негармонические колебания физического маятникаСкачать

Урок 92 (осн). Колебательное движение. МаятникиСкачать

Почти всё о маятникеСкачать

Лабораторная работа №2 - "Физический маятник"Скачать





























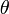 — угол отклонения маятника от равновесия;
— угол отклонения маятника от равновесия; — масса маятника;
— масса маятника;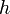 — расстояние от точки подвеса до центра тяжести маятника;
— расстояние от точки подвеса до центра тяжести маятника; — радиус инерции относительно оси, проходящей через центр тяжести.
— радиус инерции относительно оси, проходящей через центр тяжести.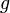 — ускорение свободного падения.
— ускорение свободного падения.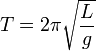

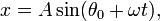
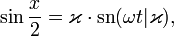
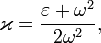


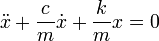
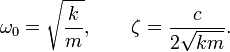
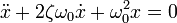

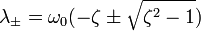

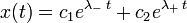

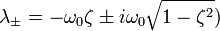
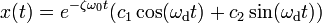
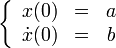


 где М – момент внешних сил;
где М – момент внешних сил;

 (4)
(4)



