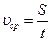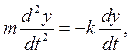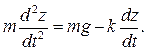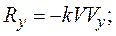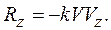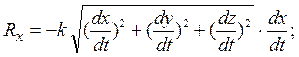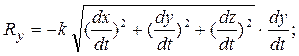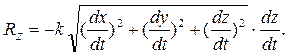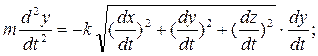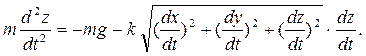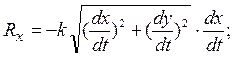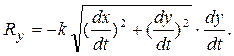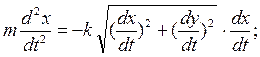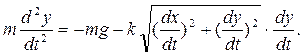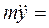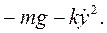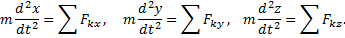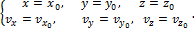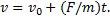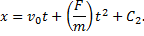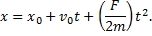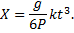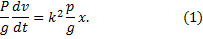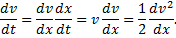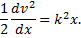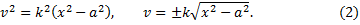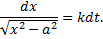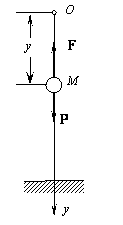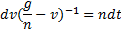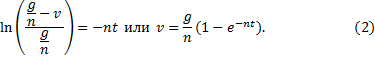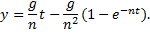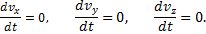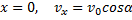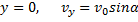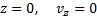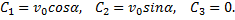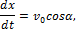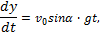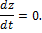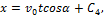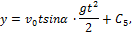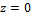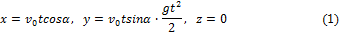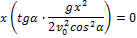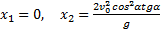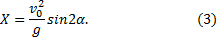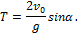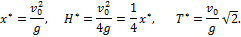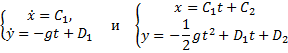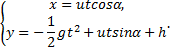Кинематика
Механика – раздел физики, изучающий механическое движение.
Механическое движение – это изменение положения тела в пространстве относительно других тел с течением времени.
Кинематика – раздел механики, изучающий геометрические характеристики механического движения.
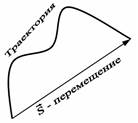
Траектория – линия, которую описывает тело при своем движении.
Путь,S – длина траектории.
Перемещение, 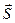
Если размеры тела намного меньше проходимого им пути, то размерами тела можно пренебречь и рассматривать его как материальную точку.
Механическое движение всегда рассматривают относительно некоторой системы отчета, которая позволяет определить характеристики этого движения.
Систему отсчета образуют тело отсчета, связанная с ним прямоугольная система координат и прибор для измерения времени (часы).
| Виды механического движения | |||
| по виду траектории | по характеру движения | ||
| прямолинейное | криволинейное | равномерное (с постоянной скоростью) | равнопеременное (с постоянным ускорением) |
Физические величины, характеризующие механическое движение
Прямолинейное равномерное движение
| Физическая величина | Формула | График зависимости от времени | Физическая величина | Формула | График зависимости от времени |
Ускорение, 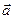 , (м/с 2 ) , (м/с 2 ) | 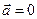 , ,  | 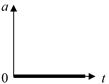 | Перемещение (путь), 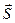 , (м) , (м) |  , , 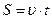 | 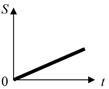 |
Скорость, 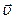 , (м/с) , (м/с) | 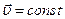 , , 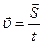 , , 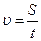 | 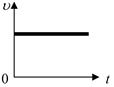 | Координата, х, (м) | 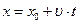 , закон движения , закон движения | 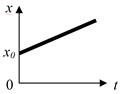 |
Прямолинейное равнопеременное движение
| Физическая величина | Формула | График зависимости от времени | Физическая величина | Формула | График зависимости от времени |
Ускорение, 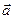 , (м/с 2 ) , (м/с 2 ) | 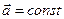 , , 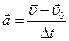 , , 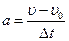 | 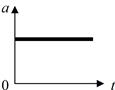 | Перемещение (путь), 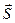 , (м) , (м) | 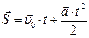 , , 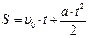 , , 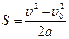 , , 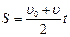 | 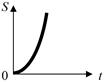 |
Скорость, 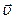 , (м/с) , (м/с) | 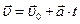 , ,  | 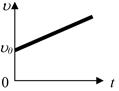 | Координата, х, (м) | 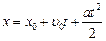 , закон движения , закон движения |  |
Средняя скорость движения:
Движение в поле силы тяжести
Свободным падением называется движение, которое совершило бы тело только под действием силы тяжести без учета сопротивления воздуха.
Видео:Движение тела, брошенного под углом к горизонтуСкачать

Составление дифференциальных уравнений.
Исследование движения материальной точки
Под действием силы тяжести в сопротивляющейся среде
В данной задаче проводится исследование движения материальной точки, находящейся под действием силы тяжести и силы сопротивления, целью которого является определение всех кинематических параметров, характеризующих это движение.
Задача относится к классу основных задач теоретической механики, и ее решение проводится на основе дифференциальных уравнений, описывающих движение материальной точки.
Решение задачи состоит из следующих операций:
1. составление дифференциальных уравнений,
2. определение начальных условий,
3. решение дифференциальных уравнений.
Составление дифференциальных уравнений.
Дифференциальные уравнения движения точки имеют вид
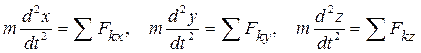
где m – масса материальной точки, x, y, z – ее координаты в произвольный момент времени, Fkx, Fky, Fkz — проекции приложенных к этой точке сил на оси координат.
Поскольку правые части этих уравнений не зависят от содержания конкретной задачи, составление дифференциальных уравнений сводится к определению суммы проекций всех приложенных к точке сил на выбранные оси координат. Для того, чтобы оформить правую часть каждого дифференциального уравнения, необходимо выполнить следующие действия
1. Выбрать систему координат, начало которой следует совместить с известным по условию задачи положением точки, а оси координат направить так, чтобы координаты движущейся точки вблизи начального положения были положительными.
2. Провести анализ каждой действующей на точку силы: определить ее направление и закономерности изменения, изобразить на чертеже и определить проекции на каждую координатную ось. Сложив проекции всех сил на каждую координатную ось, получим соответствующие правые части дифференциальных уравнений.
Составим дифференциальные уравнения точки, движущейся под действием силы тяжести в сопротивляющейся среде.
Выберем неподвижную систему координат Оxyz так (рис. 1)
чтобы относительно нее было удобно определять положение движущейся точки М. Совместим начало координат с начальным положением точки, ось z направим вертикально вверх, горизонтальные оси координат Ох и Оу направим так, чтобы при небольшом отклонении точки от начального положения ее координаты х и у были положительными.
1.2. Проведем анализ действующих на точку сил. В выбранной системе координат (рис.1) изобразим материальную точку и покажем действующие на нее силу тяжести 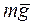
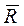

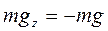
Силы сопротивления появляются в том случае, когда тело движется в какой-либо среде. Так, например, на тело, движущееся в воздухе или воде, действует со стороны этих сред сила, препятствующая движению. Действующая на тело сила сопротивления всегда направлена противоположно скорости движения. Когда относительная скорость обращается в ноль, сила сопротивления исчезает. Зависимость силы сопротивления от скорости движения носит в общем случае сложный характер. Многочисленными экспериментами установлено, что при медленном движении тела в газообразной или жидкой среде силы сопротивления пропорциональны первой степени скорости.
При более высоких скоростях имеет место так называемый квадратный или гидравлический закон сопротивления.
Наконец, при очень больших скоростях движения зависимость оказывается более сложной, однако, как в предыдущих вариантах с достаточной степенью точности можно считать, что сила сопротивления зависит только от скорости и всегда направлена против скорости.
Определим проекции сил сопротивления на оси координат для первых двух случаев.
Пусть сила сопротивления прямо пропорциональна величине скорости точки. Такая сила может быть представлена в виде векторной формулы 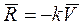
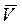
Проекции силы сопротивления на оси координат равны:
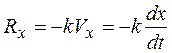
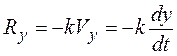
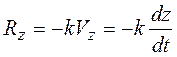
Дифференциальные уравнения движения точки принимают вид
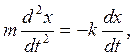
Пусть величина силы сопротивления, действующей на точку, пропорциональна квадрату скорости точки: R = kV 2. . Векторы 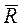
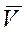
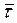
Тогда 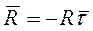
Значит 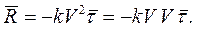
Заменим 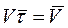
Следовательно, вектор силы сопротивления равен
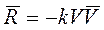
Проекции этого векторного равенства на оси координат будут равны
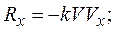
Модуль вектора скорости 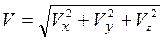
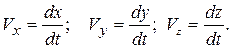
Тогда, проекции силы сопротивления на оси координат будут равны
Дифференциальные уравнения в данном случае будут записаны в виде
Если точка движется в вертикальной плоскости Оху, проекции силы сопротивления на оси координат будут равны
В этом случае будет два дифференциальных уравнения
В том случае, когда начальная скорость точки направлена вертикально по оси Оу, движение точки окажется прямолинейным. Такому движению будет соответствовать одно дифференциальное уравнение
2.Определение начальных условий заключается в том, чтобыв выбранной системе координат определить координаты точки и проекции ее скорости на оси координат в начальный момент времени. Значения указанных характеристик зависят от условия задачи и выбранной системы координат. В результате необходимо записать полученные значения при t = 0: x = x0, y = y0, z = z0,
Vx= 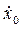
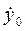
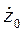
Если движение точки является плоским относительно системы координат Оху, то соответствующие начальные условия должны быть записаны в виде:
Vx= 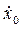
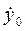
3.Решение дифференциальных уравнений. В данной работе предлагается графическое решение дифференциальных уравнений, описывающих движение материальной точки на основе компьютерной программы Mathcad.
Задание Д -2.
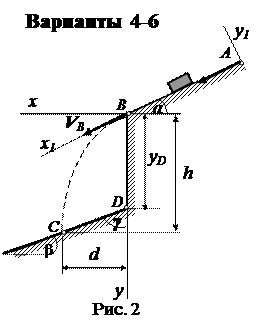
Тело массой m движется из точки А по участку АВ = l наклонной плоскости, составляющей угол α с горизонтом, в течение τ секунд. Его начальная скорость VA, коэффициент трения скольжения тела по плоскости равен f. Силой сопротивления на данном участке пренебречь.
В точке В тело покидает плоскость со скоростью VВ и падает со скоростью VС в точку С на наклонную или горизонтальную плоскость (варианты 20 – 21, 25-30) или ударяется о вертикальную плоскость(варианты 22-24), находясь в воздухе Т секунд. Положение плоскости определяется углом наклона (β или γ) или параметрами точек D и D1, через которые она проходит.
При движении в воздухе на тело действует сила сопротивления, пропорциональная скорости (варианты 1-24) или пропорциональная квадрату скорости (варианты (24-30), коэффициент пропорциональности равен k.
1. Определить все характеристики движения тела по наклонной плоскости АВ: уравнение движения, зависимость скорости и ускорения от времени, время движения по наклонной плоскости, если задана ее длина l, или ее длину, если задано время τ, значение скорости VВ в точке В.
2. Принимая во внимание силу сопротивления, составить дифференциальные уравнения движения тела в воздухе, определить траекторию этого движения, построить графики зависимости скорости и ускорения от времени, определить время движения в воздухе, установить место падения тела на заданную плоскость, определив координаты точки падения, вычислить конечную скорость .
3. Определить движение тела в воздухе без учета силы сопротивления, найти траекторию, скорость и ускорение этого движения, установить место удара тела о наклонную плоскость и его скорость в этот момент.
4. Сравнить движение тела в воздухе при наличии силы сопротивления и без нее.
Варианты 1-3.
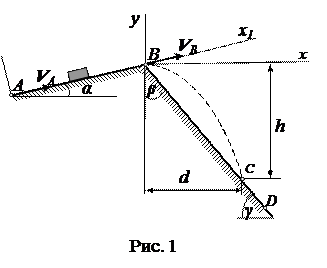
α = 15 0 ; f = 0,1; VA = 25 м/c;
l = 5 м; β = 40 0 ; k =0,4.
Вариант 2.Дано: m = 0,5 кг,
α = 20 0 ; f = 0,12; VA = 20 м/c;
τ = 3 с; γ = 45 0 ; k =2.
Вариант 3.Дано: m = 3 кг,
α = 18 0 ; f = 0,1; VA = 16 м/c;
Вариант 4.Дано: m = 1,5 кг;
Вариант 5. Дано: m = 2 кг;
τ = 3 c; β = 60 0 ; yD = — 30 м;
Вариант 6. Дано: m = 1,5 кг;
Варианты 6-9
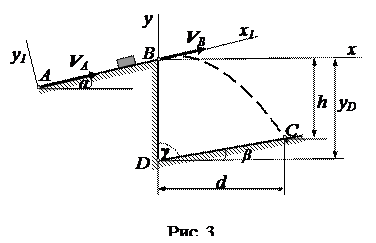
Вариант 8.Дано: m = 1 кг, α = 20 0 ; f = 0,12; τ = 3 с;
Вариант 9.Дано: m = 3 кг, α = 18 0 ;VA = 16 м/c; f = 0,1; τ = 4 с; γ =120 0 ; yD =-20 м.
Варианты 10 – 12
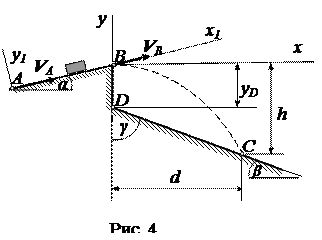
Вариант 11. m = 60 кг;
Вариант 12. Дано: m = 50 кг; α =20 0 ; VA = 20 м/c; τ = 2 с;
f = 0,2; β = 60 0 ; yD = -2,5 м; k = 12;
Варианты 13-15
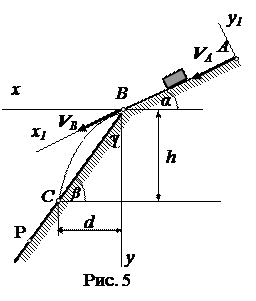
l =10 м; β = 40 0 ; k = 0,3.
Вариант 14. Дано: m = 2 кг;
τ = 3 с; γ = 34 0 ; xD= 20 м;
Вариант 15. Дано: m = 2 кг;
α =15 0 ; VA = 3 м/c; τ = 2 с
Варианты 16-18
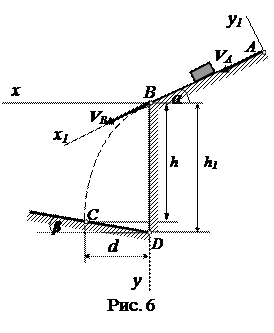
τ = 5 c; f =0,18; β= 15 0 ;
Вариант 17. Дано: m = 2 кг;
l = 8 м; yD = 38 м; k = 0,36;
Вариант 18. Дано: m = 2 кг;
l = 12 м; β = 40 0 ; yD =50 м;
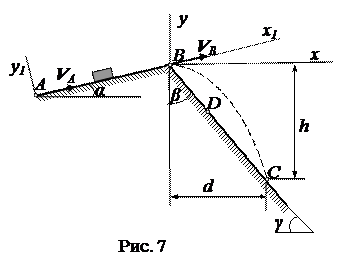
Вариант 20.Дано: m = 0,5 кг,
α = 20 0 ; f = 0,12; τ = 3 с;
Вариант 21.Дано: m = 3 кг,
α = 18 0 ; f = 0,1; VA = 16 м/c; τ = 3 с; k =0,15; γ = 40 0 .
Варианты 22-24
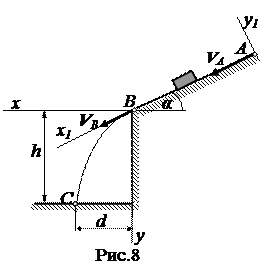
α =25 0 , VA = 12 м/c; l = 8 м;
Вариант 23. Дано: m = 4 кг;
l = 8 м; h=38 м; k =0,36.
Вариант 24. Дано: m = 4 кг;
τ = 3 c; h =40 м; k = 0, 4.
Варианты 25-27
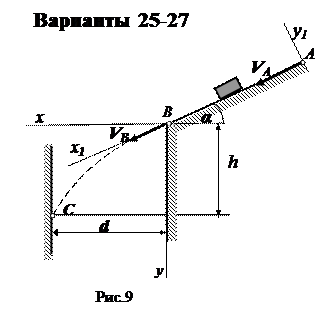
τ = 5 c; d =30 м; k = 0,2.
Вариант 26. Дано: m =0,3 кг;
f = 0,12; α = 15 0 ; τ = 6 c;
Вариант 27. Дано: m =0,3 кг; f = 0,12; α = 15 0 ; VA = 12 м/c; l = 12 м; d =40 м, k = 0,18.
Варианты 28-30
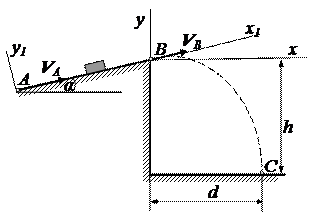
α =15 0 ; f = 0,1; VA = 25 м/c;
τ= 2 сек; h = 24 м; k =0,09.
Вариант 29. Дано:m = 4 кг;
α = 20 0 ; f =0,1; VA = 25 м/c;
l =2 5 м; h = 40 м; k =0,06.
Вариант 30. Дано: m = 4 кг;
α = 20 0 ; f = 0,1; VA = 18 м/c;
Видео:Урок 37. Движение тела, брошенного под углом к горизонту (начало)Скачать

Дифференциальные уравнения движения точки
С помощью дифференциальных уравнений движения решается вторая задача динамики. Правила составления таких уравнений зависят от того, каким способом хотим определить движение точки.
1) Определение движения точки координатным способом.
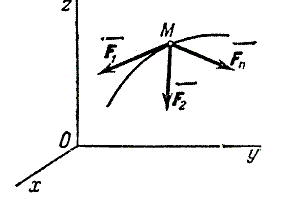
Рассмотрим свободную материальную точку, движущуюся под действием сил 
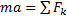
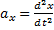
Рис.20
Так как действующие на точку силы могут зависеть от времени, от положения точки и от ее скорости, то правые части уравнений могут содержать время t, координаты точки х, у, z и проекции ее скорости 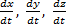
Чтобы с помощью этих уравнений решить основную задачу динамики, надо, кроме действующих сил, знать еще начальные условия, т.е. положение и скорость точки в начальный момент. В координатных осях Oxyz начальные условия задаются в виде: при t=0
Зная действующие силы, после интегрирования уравнений найдем координаты х, y, z движущейся точки, как функции времени t, т.е. найдем закон движения точки.
Пример 17. Найти закон движения материальной точки массы m, движущейся вдоль оси х под действием постоянной по модулю силы F (рис. 20.1) при начальных условиях: 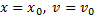
Рис.20.1
Решение. Составим дифференциальное уравнение движения точки в проекции на ось х: 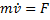
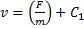
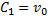
Далее, учитывая, что v = dx/dt, приходим к дифференциальному уравнению: 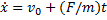
Постоянную C2 определяем из начального условия для координаты точки. Она равна 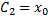
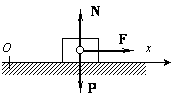
Пример 18. Груз веса Р (рис.20.2) начинает двигаться из состояния покоя вдоль гладкой горизонтальной плоскости под действием силы F = kt. Найти закон движения груза.
Рис.20.2
Решение. Выберем начало отсчета системы координат О в начальном положении груза и направим ось х в сторону движения (рис. 20.2). Тогда начальные условия имеют вид: x(t = 0) = 0, v(t = 0) = 0. На груз действуют силы F, P и сила реакции плоскости N. Проекции этих сил на ось х имеют значения Fx = F = kt, Рx = 0, Nx = 0, поэтому соответствующее уравнение движения можно записать так: 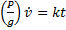
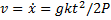
Последнее выражение, в свою очередь, является дифференциальным уравнением, интегрируя которое найдем закон движения материальной точки: 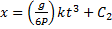
Пример 19. На груз, находящийся в покое на горизонтальной гладкой плоскости (см. рис. 20.2) на расстоянии a от начала координат, начинает действовать в положительном направлении оси x сила F = k 2 (P/g)x, где Р – вес груза. Найти закон движения груза.
Решение. Уравнение движения рассматриваемого груза (материальной точки) в проекции на ось х
Начальные условия уравнения (1) имеют вид: x(t = 0) = a, v(t = 0) = 0.
Входящую в уравнение (1) производную по времени от скорости представим так
Подставляя это выражение в уравнение (1) и сокращая на (P/g), получим
Разделяя переменные в последнем уравнении, находим, что 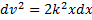
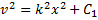
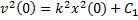
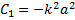
Поскольку сила действует на груз в положительном направлении оси х, то ясно, что в том же направлении он должен и двигаться. Поэтому в решении (2) следует выбрать знак «плюс». Заменяя дальше во втором выражении (2) v на dx/dt, получаем дифференциальное уравнение для определения закона движения груза. Откуда, разделяя переменные, имеем
Интегрируя последнее, находим: arch x/a=kt+C2. После нахождения постоянной C2 окончательно получаем
arch x/a=kt или 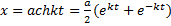
Пример 20. Шар M массы m (рис.20.3) падает без начальной скорости под действием силы тяжести. При падении шар испытывает сопротивление 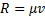
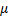
Рис.20.3
Решение. Введем систему координат с началом в точке местоположения шара при t = 0, направив ось у вертикально вниз (рис. 20.3). Дифференциальное уравнение движения шара в проекции на ось у имеет тогда вид
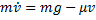
Начальные условия для шара записываются так: y(t = 0) = 0, v(t = 0) = 0.
Разделяя переменные в уравнении (1)
и интегрируя, находим: 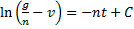
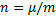
Отсюда следует, что предельная скорость, т.е. скорость при 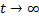
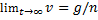
Чтобы найти закон движения, заменим в уравнении (2) v на dy/dt. Тогда, интегрируя полученное уравнение с учетом начального условия, окончательно находим
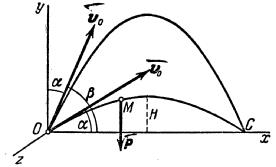
Пример 21. Изучим движение тела, брошенного с начальной скоростью v0 под углом 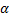
Рис.21
Поместим начало координат О в начальном положении точки. Направим ось Oy вертикально вверх; горизонтальную ось Ox расположим в плоскости, проходящей через Оy и вектор v0, а ось Oz проведём перпендикулярно первым двум осям (рис.21). Тогда угол между вектором v0 и осью Ox будет равен 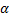
Изобразим движущуюся точку М где-нибудь на траектории. На точку действует одна только сила тяжести 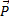
Подставляя эти величины в дифференциальные уравнения и замечая, что 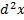
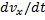
Умножая обе части этих уравнений на dt и интегрируя, находим:
Начальные условия в нашей задаче имеют вид:
Удовлетворяя начальным условиям, будем иметь:
Подставляя эти значения С1, С2 и С3 в найденное выше решение и заменяя vx, vy, vz на 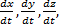
Интегрируя эти уравнения, получим:
Подстановка начальных данных даёт С4=С5=С6=0, и мы окончательно находим уравнения движения точки М в виде:
Из последнего уравнения следует, что движение происходит в плоскости Оxy.
Имея уравнение движения точки, можно методами кинематики определить все характеристики данного движения.
1. Траектория точки. Исключая из первых двух уравнений (1) время t, получим уравнение траектории точки:
Это — уравнение параболы с осью, параллельной оси Оy. Таким образом, брошенная под углом к горизонту тяжёлая точка движется в безвоздушном пространстве по параболе (Галилей).
2. Горизонтальная дальность. Определим горизонтальную дальность, т.е. измеренное вдоль оси Оx расстояние ОС=Х. Полагая в равенстве (2) y=0, найдём точки пересечения траектории с осью Ох. Из уравнения:
получаем
Первое решение дает точку О, второе точку С. Следовательно, Х=Х2 и окончательно
Из формулы (3) видно, что такая же горизонтальная дальность X будет получена при угле 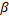
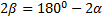
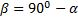
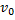
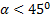
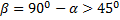
При заданной начальной скорости V0 наибольшая горизонтальная дальность в безвоздушном пространстве получается, когда 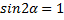
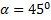
3. Высота траектории. Если положить в уравнении (2)
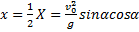
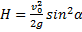
4. Время полета. Из первого уравнения системы (1) следует, что полное время полета Т определяется равенством 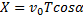
При угле наибольшей дальности 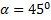
Полученные результаты практически вполне приложимы для ориентировочного определения характеристик полета снарядов (ракет), имеющих дальности порядка 200…600 км, так как при этих дальностях (и при 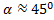
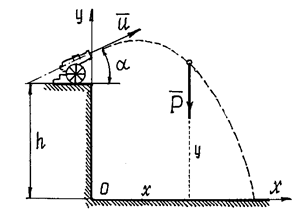
Пример 22. Из пушки, установленной на высоте h, произвели выстрел под углом 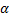
Рис.22
Чтобы правильно составить дифференциальные уравнения движения, надо решать подобные задачи по определённой схеме.
а) Назначить систему координат (количество осей, их направление и начало координат). Удачно выбранные оси упрощают решение.
б) Показать точку в промежуточном положении. При этом надо проследить за тем, чтобы координаты такого положения обязательно были положительными (рис.22).
в) Показать силы, действующие на точку в этом промежуточном положении (силы инерции не показывать!).
В этом примере – это только сила 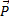
г) Составить дифференциальные уравнения по формулам: 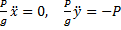
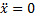
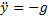
д) Решить дифференциальные уравнения.
Полученные здесь уравнения – линейные уравнения второго порядка, в правой части – постоянные. Решение этих уравнений элементарно.
Осталось найти постоянные интегрирования. Подставляем начальные условия (при t = 0 x = 0, y = h, 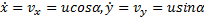
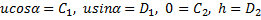
Подставляем в уравнения значения постоянных и записываем уравнения движения точки в окончательном виде
Имея эти уравнения, как известно из раздела кинематики, можно определить и траекторию движения ядра, и скорость, и ускорение, и положение ядра в любой момент времени.
Как видно из этого примера, схема решения задач довольно проста. Сложности могут возникнуть только при решении дифференциальных уравнений, которые могут оказаться непростыми.
💡 Видео
Свободное падение тел. 10 класс.Скачать

Дифференциальные уравнения движения материальной точкиСкачать
Д1 Дифференциальные уравнения движения материальной точкиСкачать

Методика решения задач по динамике материальной точки. Часть 1Скачать

Траектория и уравнения движения точки. Задача 1Скачать

Движение тела под действием силы тяжести. 1 часть. 9 класс.Скачать

Как решать задачи по динамике материальной точки.Скачать

СВОБОДНОЕ ПАДЕНИЕ ТЕЛ 9 класс ускорение свободного падения формулаСкачать

Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

Дифференциальные уравнения движения материальной точки. Часть 1Скачать

Урок 34. Свободное падение. Ускорение свободного паденияСкачать

Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Уравнение движенияСкачать

7.1. Свободное падение тела без начальной скоростиСкачать

Задача на движение материальной точки - bezbotvyСкачать

Уравнение Мещерского, формула ЦиолковскогоСкачать

Дифференциальные уравнения движения точкиСкачать

Урок 104. Импульс. Закон сохранения импульсаСкачать