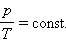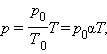Это утверждение называется законом Авогадро .
Для смеси невзаимодействующих газов уравнение состояния принимает вид
|
где , , и т. д. – количество вещества каждого из газов в смеси.
Уравнение, устанавливающее связь между давлением, объемом и температурой газа было получено в середине XIX века французским физиком Б. Клапейроном, в форме оно было впервые записано Д. И. Менделеевым. Поэтому уравнение состояния газа называется уравнением Клапейрона–Менделеева .
Следует отметить, что задолго до того, как уравнение состояния идеального газа было теоретически получено на основе молекулярно-кинетической модели, закономерности поведения газов в различных условиях были хорошо изучены экспериментально. Поэтому уравнение можно рассматривать как обобщение опытных фактов, которые находят объяснение в молекулярно-кинетической теории.
Газ может участвовать в различных тепловых процессах, при которых могут изменяться все параметры, описывающие его состояние (, и ). Если процесс протекает достаточно медленно, то в любой момент система близка к своему равновесному состоянию. Такие процессы называются квазистатическими . В привычном для нас масштабе времени эти процессы могут протекать и не очень медленно. Например, разрежения и сжатия газа в звуковой волне, происходящие сотни раз в секунду, можно рассматривать как квазистатический процесс. Квазистатические процессы могут быть изображены на диаграмме состояний (например, в координатах ) в виде некоторой траектории, каждая точка которой представляет равновесное состояние.
Интерес представляют процессы, в которых один из параметров (, или ) остается неизменным. Такие процессы называются изопроцессами .
Изотермическим процессом называют квазистатический процесс, протекающий при постоянной температуре . Из уравнения состояния идеального газа следует, что при постоянной температуре и неизменном количестве вещества в сосуде произведение давления газа на его объем должно оставаться постоянным:
|
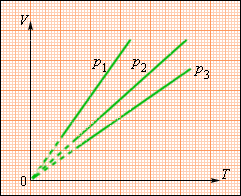
На плоскости () изотермические процессы изображаются при различных значениях температуры семейством гипербол , которые называются изотермами . Так как коэффициент пропорциональности в этом соотношении увеличивается с ростом температуры, изотермы, соответствующие более высоким значениям температуры, располагаются на графике выше изотерм, соответствующих меньшим значениям температуры (рис. 3.3.1). Уравнение изотермического процесса было получено из эксперимента английским физиком Р. Бойлем (1662 г.) и независимо французским физиком Э. Мариоттом (1676 г.). Поэтому это уравнение называют законом Бойля–Мариотта .
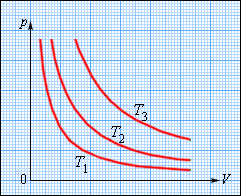 |
| Рисунок 3.3.1. |
Изохорный процесс ()
Изохорный процесс – это процесс квазистатического нагревания или охлаждения газа при постоянном объеме и при условии, что количество вещества в сосуде остается неизменным.
Как следует из уравнения состояния идеального газа, при этих условиях давление газа изменяется прямо пропорционально его абсолютной температуре: или
|
На плоскости () изохорные процессы для заданного количества вещества при различных значениях объема изображаются семейством прямых линий, которые называются изохорами . Большим значениям объема соответствуют изохоры с меньшим наклоном по отношению к оси температур (рис. 3.3.2).
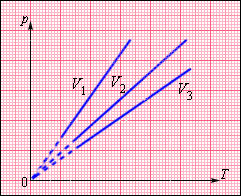 | ||||||
| Рисунок 3.3.2. Экспериментально зависимость давления газа от температуры исследовал французский физик Ж. Шарль (1787 г.). Поэтому уравнение изохорного процесса называется законом Шарля . Уравнение изохорного процесса может быть записано в виде:
где – давление газа при (т. е. при температуре ). Коэффициент , равный (, называют температурным коэффициентом давления . Изобарным процессом называют квазистатический процесс, протекающий при неизменным давлении . Уравнение изобарного процесса для некоторого неизменного количества вещества имеет вид:
где – объем газа при температуре . Коэффициент равен (. Его называют температурным коэффициентом объемного расширения газов . На плоскости () изобарные процессы при разных значениях давления изображаются семейством прямых линий (рис. 3.3.3), которые называются изобарами .
|