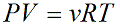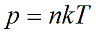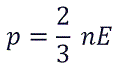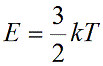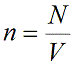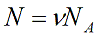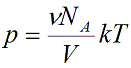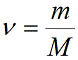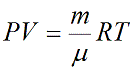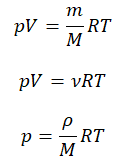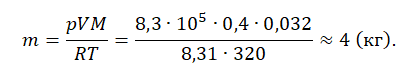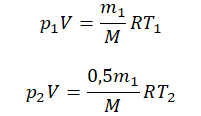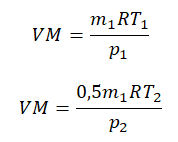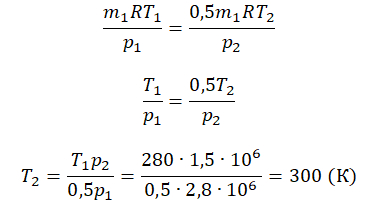Выведите уравнение клапейрона менделеева из основного уравнения молекулярно кинетической теории (5 видео)

Содержание

Уравнение состояния идеального газа Менделеева-Клапейрона с выводом
Вывод уравнения Менделеева-Клапейрона
Закон Бойля-Мариотта — изотермический процесс
Закон Гей-Люссака — изобарный процесс
Закон Шарля — изобарный процесс
Уравнение состояния идеального газа
теория по физике 🧲 молекулярная физика, МКТ, газовые законы
Выведите уравнение клапейрона менделеева из основного уравнения молекулярно кинетической теории
🔍 Видео

Видео:Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

Уравнение состояния идеального газа Менделеева-Клапейрона с выводом

Уравнение состояния идеального газа показывает корреляцию его основных макропараметров, а именно: объема V, давления P, а также температуры T.

ν — количество вещества [моль]

R – универсальная газовая постоянная, 8,31 [Дж/(моль · К)]

T – температура [K]

Данную формулу также называют уравнением Менделеева-Клапейрона для идеального газа в честь двух ученых впервые получившего (Бенуа Клапейрон (1799 – 1864)) и применившего (Дмитрий Иванович Менделеев (1834 – 1907)) его.

Видео:Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать

Вывод уравнения Менделеева-Клапейрона

Давление идеального газа зависит от концентрации частиц и температуры тела:

n — концентрация частиц [м -3 ]

k – константа Больцмана k = 1,38 · 10 -23 [Дж/К]

Т – абсолютная температура, в кельвинах [К]

Возьмем основное уравнение МКТ, выведенное через кинетическую энергию:

Подставим nkT вместо давления и выразим кинетическую энергию:

Концентрация частиц газа n равна:

N – число молекул газа в емкости объемом V [м 3 ]. N также можно представить как произведение количества вещества ν и числа Авогадро NA:

Подставим эти величины в уравнение давления идеального газа (p=nkT):

Произведение числа Авогадро N_A и константы Больцмана k дает универсальную газовую постоянную R, которая равна 8,31 [Дж/(моль · К)]. Используя это, упростим уравнение давления и получим искомое уравнение состояния идеального газа:

Учитывая, что количество вещества ν также можно определить, если известны масса вещества m и его молярная масса M:

можно привести уравнение к следующему виду:

Частными случаями уравнения являются газовые законы, описывающие изопроцессы в идеальных газах, т.е. процессы, при которых один из макропараметров (T, P, V) в закрытой изолированной системе постоянный. Всего этих частных случаев 3.

Закон Бойля-Мариотта — изотермический процесс

Проходит при постоянной температуре: T= const.

P·V = const, то есть для конкретного вещества произведение давления на объем остается постоянным:

Закон Гей-Люссака — изобарный процесс

Проходит при постоянном давлении: P = const.

V/T = const, то есть для конкретного вещества отношение объема и температуры остается постоянным:

Закон Шарля — изобарный процесс

Проходит при постоянном объеме: V = const.

P/T = const, то есть для конкретного вещества отношение давления и температуры остается постоянным:

Понравилась статья, расскажите о ней друзьям:

Видео:Физика 10 класс: Уравнение Клапейрона-МенделееваСкачать

Уравнение состояния идеального газа

теория по физике 🧲 молекулярная физика, МКТ, газовые законы

Уравнение состояния идеального газа было открыто экспериментально. Оно носит название уравнения Клапейрона — Менделеева. Это уравнение устанавливает математическую зависимость между параметрами идеального газа, находящегося в одном состоянии. Математически его можно записать следующими способами:

Уравнение состояния идеального газа

Внимание! При решении задач важно все единицы измерения переводить в СИ.

Пример №1. Кислород находится в сосуде вместимостью 0,4 м 3 под давлением 8,3∙10 5 Па и при температуре 320 К. Чему равна масса кислорода? Молярная масса кислорода равна 0,032 кг/моль.

Из основного уравнения состояния идеального газа выразим массу:

Уравнение состояния идеального газа следует использовать, если газ переходит из одного состояния в другое и при этом изменяется его масса (количество вещества, число молекул) или молярная масса. В этом случае необходимо составить уравнение Клапейрона — Менделеева отдельно для каждого состояния. Решая систему уравнений, легко найти недостающий параметр.

Подсказки к задачам

Важна только та масса, что осталась в сосуде. Поэтому:

Давление возросло на 15%	p₂ = 1,15p₁
Объем увеличился на 2%	V₂ = 1,02V₁
Масса увеличилась в 3 раза	m₂ = 3m₁
Газ нагрелся до 25 о С	T₂ = 25 + 273 = 298 (К)
Температура уменьшилась на 15 К (15 о С)	T₂ = T₁ – 15
Температура уменьшилась в 2 раза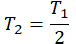
Масса уменьшилась на 20%	m₂ = 0,8m₁
Выпущено 0,7 начальной массы
Какую массу следует удалить из баллона?	Нужно найти разность начальной и конечной массы:
Газ потерял половину молекул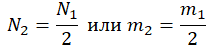
Молекулы двухатомного газа (например, водорода), диссоциируют на атомы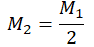
Озон (трехатомный кислород) при нагревании превращается в кислород (двухатомный газ)	M (O₃) = 3A_r (O)∙10 –3 кг/моль M (O₂) = 2A_r (O)∙10 –3 кг/моль
Открытый сосуд	Объем V и атмосферное давление p_атм остаются постоянными
Закрытый сосуд	Масса m, молярная масса M, количество вещества ν, объем V, число N и концентрация n частиц, плотность ρ— постоянные величины
Нормальные условия	Температура T₀ = 273 К Давление p₀ = 10 5 Па
Единицы измерения давления	1 атм = 10 5 Па

Пример №2. В баллоне содержится газ под давлением 2,8 МПа при температуре 280 К. Удалив половину молекул, баллон перенесли в помещение с другой температурой. Определите конечную температуру газа, если давление уменьшилось до 1,5 МПа.

2,8 МПа = 2,8∙10 6 Па

1,5 МПа = 1,5∙10 6 Па

Так как половина молекул была выпущена, m₂ = 0,5m₁. Объем остается постоянным, как и молярная масса. Учитывая это, запишем уравнение состояния идеального газа для начального и конечного случая:

Преобразим уравнения и получим:

Приравняем правые части и выразим искомую величину:

На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.

Алгоритм решения

Решение

График построен в координатах (V;E_k). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:

Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.

Запишем уравнение Менделеева — Клапейрона:

Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:

ν R = p 1 V 1 T 1 . . = p 2 V 2 T 2 . .

Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.

Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.

pазбирался: Алиса Никитина | обсудить разбор | оценить

На высоте 200 км давление воздуха составляет примерно 10 –9 от нормального атмосферного давления, а температура воздуха Т – примерно 1200 К. Оцените плотность воздуха на этой высоте.

Видео:62. Уравнение Клапейрона-МенделееваСкачать

Выведите уравнение клапейрона менделеева из основного уравнения молекулярно кинетической теории

Уравнение Менделеева-Клапейрона — уравнение состояния для идеального газа, отнесенное к 1 молю газа. В 1874 г. Д. И. Менделеев на основе уравнения Клапейрона объединив его с законом Авогадро, используя молярный объем V_m и отнеся его к 1 молю, вывел уравнение состояния для 1 моля идеального газа:

pV = RT , где R — универсальная газовая постоянная,

R = 8,31 Дж/(моль . К)

Уравнение Клапейрона-Менделеева показывает, что для данной массы газа возможно одновременно изменение трех параметров, характеризующих состояние идеального газа. Для произвольной массы газа М, молярная масса которого m: pV = (М/m) . RT. или pV = N_АkT,

где N_А — число Авогадро, k — постоянная Больцмана.

С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса газа и один из параметров — давление, объем или температура — остается постоянным, а изменяются только остальные два и получить теоретически газовые законы для этих условий изменения состояния газа.

Такие процессы называют изопроцессами. Законы, описывающие изопроцессы, были открыты задолго до теоретического вывода уравнения состояния идеального газа.

Изотермический процесс — процесс изменения состояния системы при постоянной температуре. Для данной массы газа произведение давления газа на его объем постоянно, если температура газа не меняется. Это закон Бойля — Мариотта.

Для того, чтобы температура газа оставалась в процессе неизменной, необходимо, чтобы газ мог обмениваться теплотой с внешней большой системой — термостатом. Роль термостата может играть внешняя среда (воздух атмосферы). Согласно закону Бойля-Мариотта, давление газа обратно пропорционально его объему: P₁V₁=P₂V₂=const. Графическая зависимость давления газа от объема изображается в виде кривой (гиперболы), которая носит название изотермы. Разным температурам соответствуют разные изотермы.

Изобарный процесс — процесс изменения состояния системы при постоянном давлении. Для газа данной массы отношение объема газа к его температуре остается постоянным, если давление газа не меняется. Это закон Гей-Люссака. Согласно закону Гей-Люссака, объем газа прямо пропорционален его температуре: V/T=const. Графически эта зависимость в координатах V-T изображается в виде прямой, выходящей из точки Т=0. Эту прямую называют изобарой. Разным давлениям соответствуют разные изобары. Закон Гей-Люссака не соблюдается в области низких температур, близких к температуре сжижения (конденсации) газов.

Изохорный процесс — процесс изменения состояния системы при постоянном объеме. Для данной массы газа отношение давления газа к его температуре остается постоянным, если объем газа не меняется. Этот газовый закон Шарля. Согласно закону Шарля, давление газа прямо пропорционально его температуре: P/T=const. Графически эта зависимость в координатах P-Т изображается в виде прямой, выходящей из точки Т=0. Эту прямую называют изохорой. Разным объемам соответствуют разные изохоры. Закон Шарля не соблюдается в области низких температур, близких и температуре сжижения (конденсации) газов.

Итак, из закона pV = (М/m) . RT выводятся следующие законы:

p = const => V/T = const — закон Гей — Люссака .

V= const => p/T = const — закон Шарля

Если идеальный газ является смесью нескольких газов, то согласно закону Дальтона, давление смеси идеальных газов равно сумме парциальных давлений входящих в нее газов. Парциальное давление — это такое давление, которое производил бы газ, если бы он один занимал весь объем, равный объему смеси.

Некоторых, возможно, интересует вопрос, каким образом удалось определить постоянную Авогадро N_A = 6,02·10 23 ? Значение числа Авогадро было экспериментально установлено только в конце XIX – начале XX века. Опишем один из таких экспериментов.

В откачанный до глубокого вакуума сосуд объемом V = 30 мл поместили навеску элемента радия массой 0,5 г и выдержали там в течение одного года. Было известно, что за секунду 1 г радия испускает 3,7·10 10 альфа-частиц. Эти частицы представляют собой ядра гелия, которые тут же принимают электроны из стенок сосуда и превращаются в атомы гелия. За год давление в сосуде выросло до 7,95·10 -4 атм (при температуре 27 о С). Изменением массы радия за год можно пренебречь. Итак, чему равна N_A?

Сначала найдем, сколько альфа-частиц (то есть атомов гелия) образовалось за один год. Обозначим это число как N атомов:

N = 3,7·10 10 · 0,5 г · 60 сек · 60 мин · 24 час · 365 дней = 5,83·10 17 атомов.

Запишем уравнение Клапейрона-Менделеева PV = nRT и заметим, что число молей гелия n = N/N_A. Отсюда:

N_A = NRT = 5,83 . 10 17 . 0,0821 . 300 = 6,02 . 10 23

PV 7,95 . 10 -4 . 3 . 10 -2

В начале XX века этот способ определения постоянной Авогадро был самым точным. Но почему так долго (в течение года) длился эксперимент? Дело в том, что радий добывается очень трудно. При его малом количестве (0,5 г) радиоактивный распад этого элемента дает очень мало гелия. А чем меньше газа в замкнутом сосуде, тем меньшее он создаст давление и тем большей будет ошибка измерения. Понятно, что ощутимое количество гелия может образоваться из радия только за достаточно долгое время.