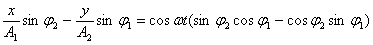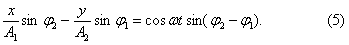Видео:Фигуры Лиссажу на осциллографеСкачать
Выведите уравнение движения точки на экране осциллографа
Лабораторная работа № 117
Градуировка звукового генератора
Цель работы: Градуировка звукового генератора методом фигур Лиссажу.
Приборы и принадлежности: электронный осциллограф, звуковой генератор.
Приведенное ниже краткое теоретическое введение должно способствовать осмысливанию сути метода фигур Лиссажу. Фигуры Лиссажу представляют собой замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским ученым Ж.Лиссажу. Вид фигуры Лиссажу зависит от соотношения между частотами, фазами и амплитудами накладываемых колебаний.
Рассмотрим вначале случай, когда материальная точка участвует одновременно в двух взаимно перпендикулярных гармонических колебаниях, происходящих с одинаковой угловой частотой w . Пусть за направления колебаний взяты оси х и у. Тогда уравнения колебаний запишутся
где A1 и A2, j 1 и j 2 – соответственно амплитуды и начальные фазы первого и второго колебаний.
Определим уравнение траектории точки, для чего исключим из уравнений (1) время. Перепишем уравнение (1) в виде:
Умножая (2) на cos j 2 и (3) на cos j 1 и беря их разность, получим
Умножая (2) на sin j 2 и (3) на sin j 1 и снова беря разность, получим
Возводя в квадрат (4) и (5) и складывая почленно, получим
Выражение (6) является уравнением траектории материальной точки, участвующей одновременно в двух взаимно перпендикулярных гармонических колебаниях с одинаковой частотой. Оно представляет собой уравнение эллипса, характеристики которого определяются значением разности фаз j 2 — j 1 . Пусть разность этих фаз
тогда уравнение траектории (6) примет вид
,
т.е. мы получили уравнение семейства прямых, проходящих через начало координат (рис. 1).
При разности фаз
уравнение (6) переходит в
т.е. в уравнение эллипса, приведенного к координатным осям, причем полуоси эллипса равны соответствующим амплитудам колебания.
Если величина полуоси вдоль оси у меньше, чем вдоль оси х (рис.2,а, А2 А1), то эллипс сплюснутый; и наоборот (рис.2,б, А2> А1) – то эллипс вытянутый. При равенстве амплитуд А1 и А2 эллипс вырождается в окружность.
Если частоты взаимно перпендикулярных колебаний не одинаковы, то траектории результирующего движения имеют вид довольно сложных кривых, называемых фигурами Лиссажу. Форма фигуры Лиссажу определяется соотношением частот и разностью начальных фаз складываемых колебаний, что наглядно видно из приведенной таблицы (рис. 3) .
Фигура Лиссажу остается устойчивой, если отношение частот взаимно перпендикулярных колебаний представляет собой рациональное число, в противном случае траектории не повторяются и вид фигуры Лиссажу непрерывно изменяется.
Описание рабочей установки и метода измерений
Если частота одного из взаимно перпендикулярных колебаний известна, то по виду фигуры можно определить частоту другого, пользуясь соотношением
где w х и w у – угловые частоты колебаний соответственно вдоль осей х и у; nу и nх – число точек пересечения фигуры Лиссажу с осями х и у.
Соотношение выражает тот факт, что чем больше угловая частота колебаний вдоль оси х, тем чаще колеблющаяся точка пересекает ось у и соответственно больше величина nу, и наоборот. Так как w =2 p n , то соотношение (9) можно записать в виде
Сравнение частот можно произвести осциллографическим методом, подавая на горизонтально отклоняющие пластины электронного осциллографа 1 пониженное напряжение из сети переменного тока с частотой n х = 50 Гц, а на вертикально отклоняющие пластины исследуемое напряжение с частотой n у со звукового генератора 2 (рис.5). При сложении взаимно перпендикулярных электрических колебаний фигуры Лиссажу наблюдаются на экране осциллографа. Частота напряжения n у определяется по формуле
вытекающей из соотношения (10).
Пусть фигура Лиссажу имеет вид, изображенный на рис.4. Число точек пересечения фигуры с осями Х и У, nх=1 и nу=2. В соответствии с формулой (11) на вертикально отклоняющие пластины осциллографа подается переменное напряжение с частотой n у = 100 Гц, меняющееся по гармоническому закону. Если ось проходит через точку пересечения ветвей фигуры, то при подсчете значений nх и nу эту точку учитывают дважды. Во избежание ошибки в этом случае оси Х и У можно параллельно самим себе переносить из центра координат. Пользуясь формулой (11), по виду фигур Лиссажу можно проградуировать шкалу частоты колебаний звукового генератора.
1. Собрать схему в соответствии с рис.5.
2. Выключить генератор развертки осциллографа (переключатель «Диапазон частот» в положении ВЫКЛ) и установить ручки усиления по осям х и у на нуль. Ручку звукового генератора «Регулировка выхода» также установить на нуль, переключатель «Множитель частот» — в положение «1».
3. Включить в сеть звуковой генератор, осциллограф. Сфокусировать и вывести световое пятно в центр координатной сетки.
4. Вращая ручку осциллографа «Усиление по оси Х», добиться горизонтальной линии на экране ½ шкалы.
5. Вращением ручки звукового генератора «Регулировка выхода» добиться появления фигуры Лиссажу.
6. Вращая ручку частоты звукового генератора от начала шкалы, добиться появления устойчивой фигуры. Фигуры перерисовать и по формуле (11) определить частоту колебаний генератора n у . Проверить, соответствует ли значение n у показанию лимба звукового генератора n лимба.
7. Оценить абсолютные и относительные ошибки в отсчетах частоты по лимбу звукового генератора.
8. Результаты измерений и вычислений занести в таблицу.
Видео:Затухающие колебания на экране осциллографа.Скачать
Изучение сложения электрических колебаний с помощью электронного осциллографа
Цель работы: изучение сложения колебаний одинакового и взаимно перпендикулярного направлений.
Приборы и принадлежности: два звуковых генератора, электронный осциллограф, два коаксиальных кабеля.
Элементы теории и метод эксперимента
Колебания — движения или процессы, обладающие той или иной степенью повторяемости во времени .
Простейшим типом периодических колебаний являются гармонические (синусоидальные или косинусоидальные) колебания, которые могут быть запи-саны в виде:
, (1)
Где X — изменяющаяся с течением времени величина; А — Амплитуда; 
— фаза; 
— ее начальное значение; 
— циклическая частота.
В случае строго гармонических колебаний величины А, , не зависят от времени.
1. Сложение гармонических колебаний одинакового направления
Рассмотрим сложение двух гармонических колебаний одинакового направления и одинаковой частоты на примере колеблющейся точки. Смещение Х Точки будет суммой смещений 
и 
, которые запишутся следующим образом:
(2)
Представим оба колебания с помощью вращающихся векторов 
и 
(рис. 1). Построим по правилам сложения векторов результирующий вектор 
.
Легко видеть, что проекция этого вектора на ось x равна сумме проекций слагаемых векторов
. (3)
Следовательно, вектор представляет собой, результирующее колебание. Этот вектор вращается с той же угловой скоростью 
, что и векторы 
и , так что результирующее движение будет гармоничесиим колебанием с частотой , амплитудой 
и начальной фазой . Из построения видно, что
(4)
Итак, представление гармонических колебаний посредством векторов дает возможность свести сложение нескольких колебаний к операции сложения векторов.
Рассмотрим несколько наиболее простых случаев сложения гармонических колебаний одинакового направления:
А) циклические частоты и фазы одинаковы, амплитуды различны:
, 
, 
,
, (5)
Т. е. возникает гармоническое колебание такой же частоты с амплитудой, равной сумме амплитуд слагаемых колебаний;
Б) циклические частоты и амплитуды одинаковы, фазы различны:
, 
,
Где — разность фаз. Тогда, применяя формулу сложения синусов, получаем
. (6)
Возникает гармоническое колебание такой же частоты, но отличающееся по фазе от первичных колебаний на половину разности фаз этих колебаний. Амплитуда
,
Вообще говоря, меньше суммы амплитуды первичных колебаний. Toлько при 
. При 
, где 
;
В) амплитуды одинаковы, циклические частоты мало отличаются друг от друга 
, 
; 
; 
. Тогда
. (7)
Результирующее колебание оказывается не гармоническим, так как оно не соответствует уравнению (1). Однако, учитывая, что
,
Можно считать результирующее колебание почти гармоническим, Имеющим циклическую частоту
,
,
Которая очень медленно периодически изменяется со временем (циклическая частота колебаний амплитуды 
слишком мала, поэтому период колебаний амплитуды 
будет большим).
Такого рода колебания называются биениями. График биений, построенный по уравнению (7), представлен на pиc. 2.
Рис. 2. Результирующие колебания, называемые биениями
Процесс возникновения и характер биений нетрудно представить себе, даже не прибегая к расчетам и рисунку. Вначале фазы слагаемых колебаний совпадают, поэтому результирующая амплитуда максимальна. Затем первое колебание постепенно отстает по фазе от второго и результирующая амплитуда будет меньше суммы амплитуд исходных колебаний. По мере нарастания разности фаз результирующая амплитуда уменьшается.
Сложение одинаково направленных колебаний можно наблюдать на экране электронного осциллографа, если синусоидальные напряжения вида
,
Где U — Мгновенная величина напряжения, 
— амплитудное значение напряжения, подать на вертикально отклоняющие пластины, а на горизонтально отклоняющие пластины — пилообразное напряжение линейной временной развертки.
2. Сложение двух взаимно перпендикулярных колебаний
Рассмотрим несколько случаев сложения двух взаимно перпендикулярных колебаний:
А) циклические частоты и фазы одинаковы, амплитуды различны:
, 
,
Где Х И у — Смещения, вызванные первым и вторым колебаниями. Тогда
. (8)
Это уравнение прямой. Следовательно, результирующее колебание совершается вдоль прямой, проходящей через положение равновесия под углом 
к направлению первого колебания (рис. 3)
. (9)
Рис. 3. Диаграмма, характеризующая результирующее колебание вдоль прямой
Величина результирующего смещения
, (10)
Где 
— амплитуда результирующего смещения;
Б) циклические частоты одинаковы, фазы различаются на 
, амплитуды различны
(11)
. (12)
Это уравнение эллипса. Следовательно, результирующее движение совершается по траектории в виде эллипса, полуоси которого равны амплитудам слагаемых колебаний (рис. 4).
Рис. 4. Диаграмма, характеризующая результирующее колебание в виде эллипса
Сопоставляя уравнение (12) и рис. 4, нетрудно установить, что точка при движении будет двигаться по часовой стрелке. Как видно из уравнения (10), в начальный момент 
а 
, т. е. тело находится в вершине эллипса. С течением времени Х Возрастает, а У Уменьшается, что согласно рис. 4 соответствует движению тела по эллипсу в направлении часовой стрелки. Очевидно, что при разности фаз, равной 
, точка описывает такой же эллипс против часовой стрелки. Если 
, уравнение эллипса переходит в уравнение окружности
. (13)
Если слагаемые Колебания имеют различную частоту, То траектории результирующего движения будут весьма сложными и разнообразными по форме — фигуры Лиссажу (см. таблицу).
Описание Формы траекторий можно непосредственно наблюдать на экране электронного осциллографа. Если на одну из пар отклоняющих пластин подать синусоидальное напряжение
,
А на другую пару
,
То при этом электронный луч будет участвовать одновременно в двух взаимно перпендикулярных колебаниях и траекторией результирующего движения при рациональном отношении частот будет одна из фигур Лиccажy.
В данной лабораторной работе для изучения сложения электрических колебаний применяются звуковые генераторы как источники этих колебаний и электронный осциллограф.
Прежде чем приступить к выполнению лабораторной работы, внимательно изучите теоретическую часть лабораторной работы №1!
Видео:Урок 342. Сложение взаимно перпендикулярных колебаний. Фигуры ЛиссажуСкачать
Изучение работы электронного осциллографа
1. Цель работы:изучение устройства, принципа действия и работы электронного осциллографа.
2. Краткая теория
Электронный осциллограф предназначен для исследования быстропеременных периодических процессов. С помощью осциллографа можно измерять силу тока и напряжение и изменение их во времени, сдвиг фаз между ними, сравнивать частоты и амплитуды различных переменных напряжений. При применении соответствующих преобразователей с помощью осциллографа можно исследовать неэлектрические процессы, например, колебания температуры, давления, изменения размеров и т. д. Электронный осциллограф позволяет наблюдать и фотографировать кратковременные процессы длительностью 
с. Регистрировать столь кратковременные процессы можно потому, что электронный луч, по смещению которого определяется искомая величина, практически безинерционен.
Электронный осциллограф представляет собой прибор, состоящий из электронно-лучевой трубки, усилителей сигналов, подаваемых на горизонтально- и вертикально-отклоняющие пластины, генератора развертки и блока питания.
В электронном осциллографе используются явления, связанные с особенностями движения заряженных частиц в электрическом и магнитном полях.
Главным элементом осциллографа является электронно-лучевая трубка. Трубка может быть с электростатическим и электромагнитным управлением. При электростатическом управлении для отклонения электронного луча используется электрическое поле. В трубках с электромагнитным управлением для этой же цели используется магнитное поле.
Рассмотрим более детально устройство электронно-лучевой трубки с электростатическим управлением.
Электронно-лучевая трубка представляет собой стеклянную вакуумную трубку (рис. 11). В узком конце трубки помещена так называемая «электронная пушка». Она состоит из цилиндрического катода 1, управляющего электрода 2 и анодов 3, 4. Катод 1 служит источником электронов и находится внутри цилиндра с отверстием (управляющего электрода) 2. На этот цилиндр подается отрицательное напряжение. Таким образом электроны, покинувшие катод, могут вылетать из цилиндра только через имеющееся в его торце отверстие, направленное в сторону флуоресцирующего экрана.
Дополнительная фокусировка электронного луча осуществляется с помощью двух цилиндрических анодов 3, 4. Оба анода имеют положительный потенциал относительно катода. Второй анод имеет более высокий положительный потенциал по сравнению с первым, поэтому между анодами создается некоторое ускоряющее электростатическое поле, которое ускоряет электроны и концентрирует их в узкий луч, иными словами, ускоряющее поле препятствует рассеянию электронов.
Проходя между двумя парами отклоняющих пластин (отклоняющие конденсаторы) 6 и 7, луч падает на экран 5, покрытый люминесцирующим веществом. В месте падения луча на экране образуется светящееся пятно. Если подать на пластины 7 постоянное напряжение, то направление движения электронного луча изменится и светящееся пятно на экране сместится вдоль вертикали. При подаче переменного напряжения луч будет колебаться в вертикальной плоскости, а на экране появится светящаяся вертикальная линия. Длина этой линии зависит от величины приложенного к пластинам напряжения.
Если постоянное напряжение подвести ко второй паре пластин 6, то пятно переместится на экране в направлении, перпендикулярном направлению первого смещения, т. е. по горизонтали. При подаче переменного напряжения получим горизонтальную линию.
Если одновременно подводятся постоянные напряжения к обоим парам отклоняющих пластин, то пятно сместится по вертикали и горизонтали. При подаче переменного напряжения одновременно к обеим парам пластин получатся фигуры Лиссажу, соответствующие сложению двух взаимно-перпендикулярных колебаний.
Вторым важным элементом электронно-лучевого осциллографа является генератор развёртки. С его помощью на пластины 6 подаётся переменное напряжение пилообразной формы (рис. 12). Под влиянием напряжения такой формы светящееся пятно на экране будет равномерно двигаться по горизонтали (например, вправо) и скачком возвращаться в крайнее левое положение. Такой периодически повторяющийся процесс, называемый горизонтальной развёрткой луча, даст на экране осциллографа светящуюся горизонтальную линию.
Если при горизонтальной развёртке луча наложить вертикальные колебания, обусловленные исследуемым напряжением, то луч на экране будет описывать кривую зависимости исследуемого напряжения от времени. Если это напряжение изменяется периодически, то, подобрав частоту развёртки, кратную частоте исследуемого напряжения, можно получить на экране неподвижный график исследуемого напряжения.
Основным из параметров, входящих в техническую характеристику электронно-лучевого осциллографа, является его чувствительность. Чувствительностью Р осциллографа к напряжению называют отклонение l (в миллиметрах) пятна на экране, вызванное разностью потенциалов 
на отклоняющих пластинах.
Определим зависимость чувствительности от параметров трубки. Пусть S — длина (см. рис. 1) пластин 7, d — расстояние между пластинами, L — расстояние от конца пластины до экрана, U — потенциал анода по отношению к катоду, 
— разность потенциалов между отклоняющими пластинами 7. Считаем, что управляющие пластины параллельны, а электрическое поле однородно и перпендикулярно к плоскости пластин. Тогда, в области между пластинами 7, т. е. по оси Y, электрон движется равноускоренно и его смещение при выходе из области между пластинами будет равно:
, (1)
а его ускорение
. (2)
Здесь 
и 
— заряд и масса электрона, Е — напряженность электрического поля между пластинами, 
— сила, действующая на электрон, находящийся в электрическом поле, 
— время пролёта электрона между пластинами, определяемое соотношением:
, (3)
где 
— горизонтальная составляющая скорости. Эта составляющая скорости вызвана действующей разностью потенциалов между анодом и катодом U и определяется из условия:
. (4)
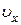
Подставляя (2) и (3) в (1), получим
Отклонение 
в области вне пластин может быть записано в виде:
, (5)
где 
есть скорость по оси Y, которую электрон приобретает при вылете из пространства между пластинами. Эта скорость 
, а время пролёта электроном расстояния равно
.
Подставляя значения a, 
и 
в формулу (5), получим для Y2 выражение
.
Полное отклонение 
будет равно:
(6)
(так как 
).
Подставляя 
из (4) получим, что полное отклонение электронного луча
, (7)
а чувствительность Р будет равна:
. (8)
Таким образом, чувствительность зависит от размера пластин, их расстояния до экрана и напряжения между анодом и катодом, а смещение зависит дополнительно и от напряжения между отклоняющими пластинами.
Описание установки
Лабораторная установка состоит из электронного осциллографа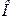 
, звукового генератора 
и потенциометра 
с трансформатором и вольтметром (рис. 14-16). Звуковой генератор позволяет получать синусоидальные электрические колебания в звуковом диапазоне частот от 20 
до 20 
, а потенциаметр частотой 50 , при этом величина напряжения может плавно изменяться и контролироваться с помощью вольтметра.
Панель управления электронного осциллографа
На передней панели осциллографа расположены ручки (у некоторых марок осциллографов отдельные из них могут быть вынесены на верхнюю часть корпуса), с помощью которых можно управлять электронным лучом, а также клеммы вертикального «вход Y» и горизонтального «вход X» входов. На рис. 13 изображена одна из типичных панелей осциллографа.
1. Яркость свечения пятна на экране зависит от количества электронов, ударяющихся об экран в единицу времени и от их скорости. Меняя отрицательный потенциал управляющего электрода 2 (см. рис. 11) и, тем самым, изменяя количество электронов, проходящее через отверстие, можно регулировать яркость пятна на экране — ручка «яркость».
2.Фокусировка электронов в одну точку на экране осуществляется изменением разности потенциалов между первым 3 и вторым 4 анодами (рис. 11) — ручка «фокус».
3.Смещение изображения в вертикальном направлении производится при помощи ручки «Y» (вверх-вниз), а в горизонтальном — ручкой «X» (влево-вправо).
4.Переключатель «ослабление» позволяет уменьшить исследуемый сигнал, подаваемый на входные клеммы осциллографа «вход Y» и «вход X» в десять или в сто раз.
5.Ручки «усиление по вертикали» и «усиление по горизонтали» дают возможность плавно регулировать амплитуду колебания по оси Y и по оси X.
6.К органам управления генератора развертки относятся ручки: «диапазоны частот» и «частота плавно». Первая даёт возможность выбрать нужный диапазон частот для непрерывной развёртки. Вторая — в пределах выбранного диапазона изменять собственную частоту непрерывных пилообразных колебаний генератора развёртки.
Для устранения перемещения изображения по экрану применяется синхронизация частоты генератора с частотой исследуемого напряжения (внутренняя) либо с частотой какого-нибудь внешнего напряжения (внешняя синхронизация) — ручка «синхронизация».
Порядок выполнения работы
Ознакомьтесь со схемой осциллографа и его устройством по данному описанию и плакатам, определите назначение всех ручек управления.
Подготовка осциллографа к работе
1.Ручки с указателями «фокус», «Y» и «X» перевести в среднее положение, ручку с указателем «яркость» — в крайнее правое положение.
2.Установить переключатель «синхронизация» в положение «внутрь».
3.Включить осциллограф в сеть, при этом загорится сигнальная лампочка. Через 1-2 мин, когда прогреются лампы прибора, на экране появится зелёная точка.
4.Проверьте действие ручек, управляющих электронным лучом: «яркость», «фокус», «Y», «.X» и установите чётко светящуюся точку в центре экрана.
5.Включите генератор развёртки, при этом на экране появится светящаяся горизонтальная линия.
Задание 1Определение чувствительности осциллографа
Для определения чувствительности осциллографа необходимо собрать схему осциллографа и потенциометра (с вольтметром и трансформатором), приведенную на рис. 14.
Изменение отклонения луча в миллиметрах от оси трубки, получающееся при изменении напряжения на входе осциллографа на 1 вольт, называется его чувствительностью. Определение чувствительности осциллографа производится в следующем порядке:
1.Выключить генератор развёртки.
2.Включить потенциометр в сеть переменного тока и с движка потенциометра подать напряжение на вход вертикального усилителя при максимальном усилении — «вход Y».
3.Подаваемое переменное напряжение контролировать вольтметром переменного тока.
4.По шкале, укреплённой на экране осциллографа, измерить длину появившейся на экране светящейся вертикальной линии.
Обычно вольтметры переменного тока измеряют эффективные значения напряжения, а осциллограф измеряет амплитудные значения тех же величин, причем длина вертикальной линии на экране осциллографа пропорциональна удвоенному значению амплитуды. Поэтому чувствительность осциллографа можно рассчитать по формуле:
,
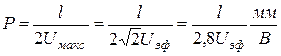
где l — длина линии на экране в мм; 
— напряжение на вольтметре;
— максимальное значение напряжения.
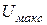
Измерение надо произвести 5-7 раз при различных напряжениях на входе осциллографа. Результаты занести в табл. 1 и построить график в координатах 
. Определить погрешность измерения чувствительности осциллографа.
| № измерения | Напряжение, подаваемое на клеммы вертикального усиления | Размер полосы на экране 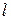 , мм | Чувствительность осциллографа, 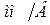 | Средняя чувствительность | Погрешность |
С помощью градуировочного графика осциллограф можно использовать как вольтметр, измеряющий амплитудные (максимальные значения напряжений).
Задание 2.Наблюдение на экране осциллографа синусоидально меняющегося напряжения
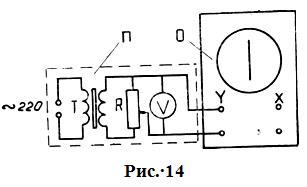
Для наблюдения на экране осциллографа синусоидально меняющегося напряжения необходимо не выключая схему, приведённую на рис. 14, произвести следующие действия.
1. Включить генератор развёртки.
2.Ручкой «частота плавно» добиться стабильности изображения, т. е. полностью сделать его неподвижным.
3.Меняя напряжение, подаваемое на вертикально отклоняющие пластины ручкой «усиление», проследить за изменением кривой на экране.
4.Меняя частоту генератора развёртки с помощью ручек «диапазоны частот» и «частота плавно», получить ряд многопериодных синусоид.
Задание 3.Наблюдение изменения формы синусоидального напряжения после прохождения тока через полупроводниковый диод
Для наблюдения изменения формы синусоидального напряжения после прохождения тока через диод используется предыдущая схема. При этом необходимо дополнительно между выходом с потенциометра и входом «вход Y» осциллографа включить полупроводниковый диод и перемкнуть входные клеммы осциллографа сопротивлением, которое будет выполнять роль нагрузки (рис.15). В данном случае диод будет действовать как однополупериодный выпрямитель. На экране осциллографа будет наблюдаться одна полуволна. Получаемые фигуры зарисовать в тетради.
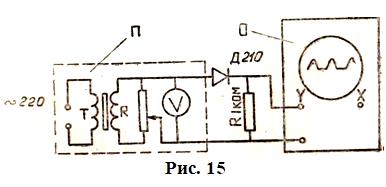
Задание 4.Определение частоты подаваемого напряжения методом фигур Лиссажу
Как известно, в случае сложения двух взаимно-перпендикулярных колебаний точка на экране движется по кривым, называемым фигурами Лиссажу.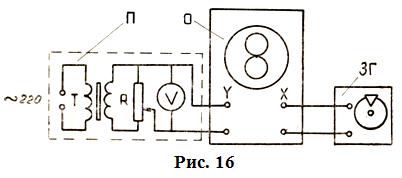 
Конфигурация этих кривых зависит от соотношения амплитуд, начальных фаз и частот составляющих колебаний. По форме устойчивых фигур Лиссажу можно, в частности, определить соотношение частот. Для этого на вертикальный вход осциллографа «вход Y» от потенциометра подают электрические колебания с частотой 50 Гц, а на горизонтальный вход «вход X» от генератора ЗГ — электрические колебания, частоту которых можно изменять.
Для получения фигур Лиссажу необходимо:
1. Выключить генератор развёртки.
2. Собрать схему в соответствии с рис. 16.
3. Включить приборы в сеть.
4. Изменяя частоту электрических колебаний, поступающих от звукового генератора, получить фигуры Лиссажу для соотношения частот 
2:1 (50Гц:25Гц); 1:1 (50Гц:50Гц); 1:2 (50Гц:100Гц); 1:3 (50Гц: 150Гц) и т. д. (всего не менее 5-ти фигур).
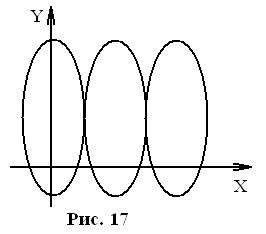
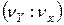
5. Если частота одного из колебаний известна, то по виду фигур Лиссажу можно определить частоту другого колебания. Для этого подсчитывают число точек пересечения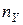 
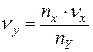
фигуры Лиссажу с осью Y и число точек пересечения 
той же фигуры с осью X (рис. 17). Пользуясь формулой 
находят искомую частоту:
.
6. Результаты наблюдений и измерений занести в табл. 2.
| Вид фигур Лиссажу | Число точек пересечения 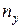 | Число точек пересечения | Частота  , Гц | Частота расчётная 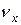 , Гц | Показания по лимбу звукового генератора | Отношение частот |
| · · · n |
Отчёт по работе выполняется в соответствии с общими требованиями. При этом в отчёте должны быть: схема электронно-лучевой трубки, объяснение принципа получения развёртки подаваемого на вход осциллографа сигнала, расчётный и графический материал в соответствии с заданиями 1-4.
Контрольные вопросы
1. Назначение электронного осциллографа.
2. Устройство и принцип действия осциллографа.
3. Какие силы действуют на электрон, пролетающий между пластинами осциллографа с электростатическим и электромагнитным управлением электронным лучом?
4.Как расчётным образом определить (по параметрам электронно-лучевой трубки) чувствительность осциллографа?
5.Как экспериментально определить чувствительность осциллографа?
6.Что такое эффективное и амплитудное значения напряжения? Какое из них наблюдаем на экране осциллографа?
7.Каким образом развёртывается во времени поступающий на вход осциллографа сигнал? Что такое генератор развёртки?
8.Какие включения необходимо произвести (включение развёртки, подача сигналов на вход Y и X осциллографа) для получения на экране: 1) горизонтальной линии; 2) вертикальной линии; 3) синусоиды; 4) фигуры Лиссажу?
9.Что такое фигуры Лиссажу и как по ним можно определить частоту неизвестного источника тока?
📽️ Видео
Урок 7. Осциллограф.Скачать
Только не говори никому.. Как легко можно восстановить жидкокристаллический экран..Скачать
Сложение взаимно перпендикулярных гармонических колебанийСкачать
Урок 327. Гармонические колебанияСкачать
Фигуры Лиссажу: осциллограф.Скачать
4 Фигуры ЛиссажуСкачать
Урок 343. Затухающие колебания (часть 1)Скачать
Как вывести фигуры Лиссажу на осциллограф (Tutorial)Скачать
Урок 353. Колебательный контурСкачать
МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать
Урок 335. Анализ графика гармонических колебанийСкачать
6.27.Щуп делитель 1:20 для осциллографа на 800 В с гальванической развязкой.Скачать
Лекция №11 "Колебания" (Булыгин В.С.)Скачать
Разные фигуры ЛиссажуСкачать
Фигуры Лиссажу на осциллографеСкачать
Проверка исправности радиодеталей осциллографом.Скачать
Как научиться пользоваться ОсциллографомСкачать
