Вынужденные колебания дифференциальное уравнение вынужденных колебаний его решение и анализ (4 видео)

Вынужденные колебания

Содержание

Определение вынужденных колебаний
Дифференциальное уравнение вынужденных колебаний
Резонанс вынужденных колебаний
Примеры задач с решением
Вынуяеденные колебания. Резонанс
Вывод дифференциального уравнения вынуяеденных колебаний пружинного маятника
Дифференциальное уравнение вынужденных колебаний и его решение
Дифференциальное уравнение вынужденных колебаний и его решение. Период и амплитуда вынужденных колебаний
🔍 Видео

Видео:Урок 347. Вынужденные колебания. Резонанс (часть 1)Скачать

Определение вынужденных колебаний

Для того чтобы в реально существующей колебательной системе получать незатухающие колебания, следует каким-либо образом компенсировать потери энергии, которые происходят в результате существования сил сопротивления. Самым простым способом реализации незатухающих колебаний является воздействие на систему при помощи внешней периодической силы. Работа внешней силы обеспечить приток энергии в систему извне. Эта энергия не даст колебаниям затухнуть, при действии сил трения.

Колебания, которые возникают под действием периодически меняющейся силы (периодически изменяющейся ЭДС), называют вынужденными механическими (электромагнитными) колебаниями.

Видео:Вынужденные колебания и дифференциальное уравнениеСкачать

Дифференциальное уравнение вынужденных колебаний

Допустим, на механическую колебательную систему действует гармонически изменяющаяся внешняя сила:

Рассмотрим колебания груза на пружине (пружинный маятник). Уравнение незатухающих гармонических колебаний для этой системы можно записать как:

где $x$ — координата; $delta $ — коэффициент затухания; $_0$ — циклическая частота свободных незатухающих колебаний (если $delta $=0, то $_$называют собственной частотой колебаний).

Если рассматривается, например, электрический колебательный контур, то роль периодически действующей силы может играть внешняя ЭДС или переменное напряжение. Их подводят к контуру извне и изменяются они по гармоническому закону. Уравнение колебаний в электрическом контуре можно представить как:

где $q$ — заряд; $delta =frac$ — коэффициент затухания; $_0=frac<sqrt>$; $U=U_m$ — внешнее переменное напряжение.

Уравнения (2) и (3) можно свести к линейному неоднородному дифференциальному уравнению вида:

где $s$ — колеблющийся параметр; $x_0=frac$ если колебания механические ($x_0=frac— в случае электрических колебаний$).

Решением уравнения (4) является сумма общего решения однородного уравнения и частного решения неоднородного уравнения. Однородное уравнение при этом имеет вид:

Его общее решение:

где $A_0$ — начальная амплитуда колебаний.

Частное решение уравнения (4) в представлено выражением:

Слагаемое $s_1$ в решении уравнения (5) играет значительную роль в начальной стадии установления колебаний, пока амплитуда вынужденных колебаний не будет определяться выражением (8).

Установившись, вынужденные колебания происходят с частотой $omega $ и являются гармоническими. Амплитуда и фаза этих колебаний определяются равенствами (8) и (9), и они зависят от частоты $omega $.

Видео:71. Вынужденные колебанияСкачать

Резонанс вынужденных колебаний

Если частота вынуждающей силы приближается к собственной частоте колебаний, то возникает резкое увеличение амплитуды колебаний. Такое явление называют резонансом.

Из выражения (8) видно, что амплитуда имеет максимум. Для нахождения резонансной частоты (частоты при которой $A=max$), следует найти максимум функции $A(omega )$. Взяв производную $frac$ и приравняв ее к нулю получим:

Равенство (10) справедливо при:

Получается, что резонансная частота ($_r$) равна:

При $^2ll ^2_0$ резонансная частота совпадает с собственной частотой колебаний $_0.$ Подставим вместо частоты правую часть выражения (11) в формулу (8), получим выражение для резонансной амплитуды вынужденных колебаний:

При небольшом затухании колебаний (если $^2ll ^2_0$) амплитуда при резонансе равна:

где $Q=frac<_0>$ — добротность колебательной системы, величина, характеризующая резонансные свойства колебательной системы. С увеличением добротности увеличивается амплитуда резонанса.

Видео:Вынужденные колебания. Резонанс | Физика 11 класс #9 | ИнфоурокСкачать

Примеры задач с решением

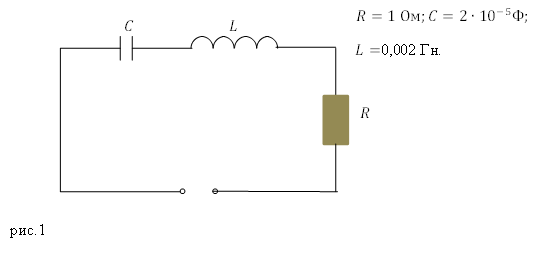
Задание. Какова добротность колебательного контура, представленного на рис.1?

Решение. Добротность электрического колебательного контура найдем как:

При этом собственная частота колебаний в таком контуре равна:

коэффициент затухания находим как:

Подставляет правые части выражений (1.2) (1.3) вместо соответствующих величин в (1.1), в результате, добротность представленного на рис. 1 контура найдем при помощи формулы:

Ответ. $Q=10$

Задание. Пружинный маятник выполняет вынужденные колебания в вязком веществе. Масса груза на пружине равна $m$, коэффициент упругости пружины $k$. Коэффициент сопротивления среды равен $r$. Систему заставляет совершать колебания сила $F=$Чему равна резонансная амплитуда заданных колебаний ($A_r$)?

Решение. Допустим, что груз совершает колебания вдоль прямой X, тогда уравнением данных механических колебаний будет выражение:

где коэффициент затухания равен $delta =frac$. Из функции, которая задает вынуждающую силу:

мы видим, что амплитуда силы равна единице:

Собственная частота колебаний груза на пружине:

Амплитуда при резонансе таких колебаний равна:

Видео:Урок 343. Затухающие колебания (часть 1)Скачать

Вынуяеденные колебания. Резонанс

В реальных колебательных системах всегда имеют место потери энергии, что приводит к затуханию колебаний. Система совершает незатухающие колебания, когда на неё действует внешняя, периодически изменяющаяся сила, компенсирующая потери энергии.

Колебания, возникающие в системе под действием периодической внешней силы, называются вынуяеденными. Переменная внешняя сила, приложенная к колебательной системе и вызывающая вынужденные колебания, называется вынуждающей силой F (О-

В колебательном контуре компенсируются потери энергии, если в контур включён источник электрической энергии, основными характеристиками которого являются электродвижущая сила (ЭДС) и внутреннее сопротивление.

Источник электрической энергии в электротехнике называют источником ЭДС (источником напряжения). В механических системах потери энергии компенсируются работой внешних сил по преодолению сил трения.

Видео:Затухающие колебания. Вынужденные колебания | Физика 9 класс #26 | ИнфоурокСкачать

Вывод дифференциального уравнения вынуяеденных колебаний пружинного маятника

Вынужденные колебания пружинного маятника происходят под действием вынуждающей силы F _ehm.(t), изменяющейся со временем t по гармоническому закону с циклической частотой со

где F вын.(0 — мгновенное значение (в момент времени г) вынуждающей силы,

F т.вын — амплитуда колебаний вынуждающей силы.

На колебательную систему, кроме вынуждающей силы F _вын, одновременно действуют упругая сила F_vnp и сила трения F_mp, равные

где к — коэффициент упругости пружины, г — коэффициент пропорциональности.

Уравнение движения тела массой пружинного маятника, по второму закону Ньютона, имеет вид

Пусть маятник движется вдоль оси о х (рис. 190). Запишем уравнение (19.81) в проекции на ось ох

разделим уравнение на т — массу тела и введём обозначения

тогда получим дифференциальное уравнение вынужденных колебаний пружинного маятника

Вывод дифференциального уравнения вынужденных колебаний в электрическом колебательном контуре

В реальном электрическом колебательном контуре электрическое сопротивление R отлично от нуля (рис.191). Поэтому, если возникают свободные колебания в контуре, то они постепенно затухают.

Формула закона Ома для участка цепи 1 -R-L-2 имеет вид

где (g>i — q>2) — разность потенциалов обкладок конденсатора,

равная qjj— (р-> = iL,

С q — электрический заряд на обкладках конденсатора,

С — ёмкость конденсатора,

J — сила электрического тока, J = С 1Я_,

Е (t) — электродвижущая сила (ЭДС) внешнего источника напряжения

Запишем уравнение (19.83) в виде

затем разделим на индуктивность катушки L и введём обозначения

где р — коэффициент затухания свободных колебаний,

а>₀ — циклическая частота свободных затухающих колебаний, когда

сопротивление R контура равно нулю (R = 0).

Подставим эти обозначения в (19.84)

Формула (19.85) представляет собой дифференциальное уравнение вынуяеденных колебаний в электрическом колебательном контуре.

Уравнения (19.85) и (19.82) аналогичны друг другу, поэтому заменим их уравнением вида

электрического колебательного контура S = q, 2ft = ,со₀ = 1 .

Уравнение (19.86) является линейным неоднородным (с правой частью, отличной от нуля) дифференциальным уравнением второго порядка. Общее решение этого уравнения представляет собой сумму решения однородного уравнения (S _одн) и частного решения (S _част) неоднородного уравнения

Однородное уравнение для колеблющейся величины S имеет вид

Для пружинного маятника S = х, 2/3 = —,со₀ 2 = —, F₀ =f _т._вЬ1Н, а Д ля

где частота со равна

Уравнение (19.88) описывает собственные затухающие колебания величины S. Они прекращаются через некоторый интервал времени (множитель е убывает со временем по экспоненте, поэтому им можно пренебречь).

Величина S совершает незатухающие (установившиеся во времени) вынужденные колебания, описываемые частным решением уравнения (19.87)

где А — амплитуда колебаний, А = S _тах,

со — циклическая частота колебаний, равная циклической частоте вынуждающей силы,

А ср — сдвиг по фазе между вынуждающей силой и вынужденными колебаниями.

На рис. 192 показан график установившихся вынужденных колебаний величины S. Характер вынужденных колебаний определяется, как величиной внешней силы, так и свойствами колебательной системы. Собственные затухающие колебания имеют место в течение интервала времени t = t _раск , когда происходит раскачка колебательной системы.

Время раскачки t _раск зависит от коэффициента затухания Д чем меньше величина Д тем больше это время. Когда прекращаются собственные затухающие колебания, система совершает вынужденные (незатухающие) установившиеся колебания.

Характер вынужденных колебаний изменяется со временем, когда начинает действовать внешняя периодическая сила. Только через некоторое время устанавливаются вынужденные колебания, период Т которых равен периоду внешней силы. Вынужденные колебания возникают тем быстрее, чем больше затухание собственных колебаний в колебательной системе.

Для вывода формул, определяющих амплитуду А установившихся вынужденных колебаний и сдвиг по фазе А C L_§_ в уравнение (19.86)

Каждое слагаемое в данном уравнении описывает гармонически изменяющуюся величину, но для всех слагаемых одинаковая частота со и различные фазы колебаний.

Первое слагаемое на векторной диаграмме (рис. 193) изображается вектором, длина которого равна А со ”. Он направлен в отрицательном направлении горизонтальной оси (противоположно вектору, представляющему третье слагаемое). Третье слагаемое, стоящее в левой части уравнения, представлено на векторной диаграмме вектором, длиной А со₀ 2 , направленным по горизонтальной оси в положительном направлении (вправо).

Второе слагаемое на векторной диаграмме изображается вектором длиной, равной 2А /> со. Этот вектор повёрнут от

горизонтальной оси на угол 71 против часовой стрелки.

На рис. 194,195 представлен результат сложения трёх векторов, когда со со₀.

Векторная сумма векторов с длинами, равными 2А [3 со и А со₀ 2 должна быть равна вектору длиной F₀ (рис. 194).

Результат сложения векторов зависит от соотношения частот со

и С0о. Суммарный вектор длиной F₀ является диагональю

прямоугольника со сторонами 2А /3 со и А (со₀ со ). Он составляет с

горизонтальной осью угол А со_а. В формуле стоит квадрат выражения (со 2 ,, — со 2 ) 2 .

Согласно (19.90), амплитуда А вынужденных колебаний зависит от соотношения собственной частоты со₀ и частоты со вынуждающей силы, а так же от коэффициента затухания /1. Заметим, что увеличение амплитуды колебаний ограничено, независимо от соотношения частот со₀ и со. Это объясняется тем, что с ростом амплитуды увеличивается скорость колебательного движения, а вместе с ней и сила трения (сила сопротивления). Колебательная система интенсивно расходует энергию. Тогда амплитуда автоматически принимает значение, при котором прибыль энергии извне компенсирует расходы на преодоление трения (на излучение и др.).

Сдвиг по фазе А ср, как следует из векторной диаграммы, определяется формулой

Из формул (19.90) и (19.91) следует, что амплитуда А вынужденных колебаний и сдвиг по фазе А ср между вынужденными колебаниями и вынуждающей силой определяются параметрами, характеризующими вынуждающую силу, такими, как амплитуда А, частота со, а так же параметрами колебательной системы, а именно, собственной частотой колебаний со₀, коэффициентом затухания /1.

В механической колебательной системе (пружинный маятник) величины А и А ср зависят от массы т колеблющего тела, а у электрического колебательного контура — индуктивности L катушки. Амплитуда А и сдвиг по фазе А ср установившихся вынужденных колебаний не зависят от времени t и начальных условий.

Вынужденные колебания отстают по фазе от вынуждающей силы, вызывающей их, на величину А ср, зависящую от частоты со вынуждающей силы, которая периодически изменяется во времени. Объясним, почему это происходит на примере механической колебательной системы (пружинного маятника).

Считаем, что в начальный момент времени (t = 0) он покоится. Вынуждающая сила F (?) равна нулю. Затем внешняя сила F (?) смещает тело массы т из положения равновесия, совершая положительную работу.

Через четверть периода (t = Т_) величина внешней силы F (7) и

смещения х достигают максимального значения. Затем, внешняя сила убывает со временем, а тело под действием возвращающей силы (силы упругости F у„р) движется к положению равновесия.

При отсутствии внешней силы тело вернулось бы в положение равновесия (начальное положение) через промежуток времени, равный четверти собственного периода колебаний.

В реальных условиях внешняя сила, убывая по величине со временем, тормозит движение тела. Она совершает отрицательную работу.

Тело движется замедленно, скорость его уменьшается. Колебания пружинного маятника начинают отставать от колебаний вынуждающей силы, опережающей смещение тела.

Следует заметить, что параметры, характеризующие вынужденные колебания, происходящие под действием внешней периодической силы, определяются добротностью Q.

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Дифференциальное уравнение вынужденных колебаний и его решение

Рассмотрим теперь случай, когда в системе наряду с силами упругости и трения присутствует некоторая внешняя сила, препятствующая затуханию колебаний. Предположим, что эта вынуждающая сила F_в действует периодически с круговой частотой w_в и зависит от времени по закону : F_в = F_о sin w_в t , где F_о — амплитуда вынуждающей силы.

Для этого случая дифференциальное уравнение (второй закон Ньютона) имеет вид:

(13)

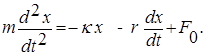
Сохраняя обозначения к / m = w ₀ 2 , r / m = 2b , и обозначив F₀ /m = f₀ приведем уравнение (13) к виду:

sin w_в t (14)

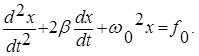
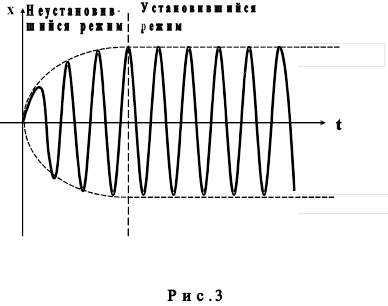Вынужденные колебания дифференциальное уравнение вынужденных колебаний его решение и анализ

Решение этого уравнения представляет некоторую функцию, которая графически представлена на рис. 3. Это решение состоит из двух частей. Одна из них соответствует неустановившемуся режиму колебаний, когда их амплитуда зависит от времени. Вторая часть описывает установившийся режим колебаний.

В установившемся режиме вынужденных колебаний смещение х подчиняется гармоническому закону и происходит с частотой, равной частоте действия вынуждающей силы:

Установившаяся амплитуда А вынужденных колебаний, зависит от параметров системы (частоты собственных колебаний w ₀ и коэффициента затухания b) и от характеристик вынуждающей силы (f₀ и w_в):
А = f (w₀ ,b , f₀ ,w _в). Строгое рассмотрение приводит к следующим выражением для значений А и j₀ , входящих в формулу (15):

(16)

(17)

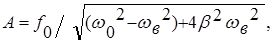
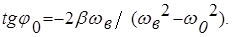
Из рассматриваемой формулы (16) следует, что амплитуда достигает максимального значения А_mах при определенном соотношении между величинами w₀ ,w _в и b .

Минимум знаменателя в формуле (16) достигается при условии:

w _в = w_рез 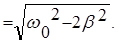(18)

То есть, амплитуда вынужденных колебаний максимальна, если частота действия вынуждающей силы определяется формулой (18). Явление резкого возрастания амплитуды вынужденных колебаний при частоте действия вынуждающей силы, определяемой формулой (16), называется резонансом.

Если бы затухание в системе отсутствовало (b = 0), то резонанс наступал бы при условии (w₀ = w _в) и при этом амплитуда достигала бы бесконечно большого значения.

Дата добавления: 2016-01-20 ; просмотров: 1416 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Физика 9 класс (Урок№11 - Гармонические колебания. Затухающие колебания. Резонанс.)Скачать

Дифференциальное уравнение вынужденных колебаний и его решение. Период и амплитуда вынужденных колебаний

Вынужденные колебания — это колебания, происходящие под действием периодического внешнего воздействия. Рассмотрим колебания грузика на пружине (рис. 6.5), если к нему (наряду с силой упругости F = -kx и силой сопротивления F_c = -rv) приложена внешняя сила, изменяющаяся по гармоническому закону:

По аналогии с формулой (5.21)

В соответствии с теорией дифференциальных уравнений установившееся решение неоднородного (с ненулевой правой частью) дифференциального уравнения вынужденных колебаний (6.10) имеет вид гармонической функции, изменяющейся с частотой внешнего воздействия