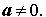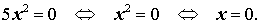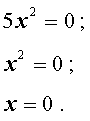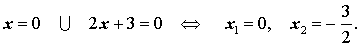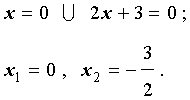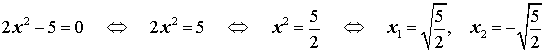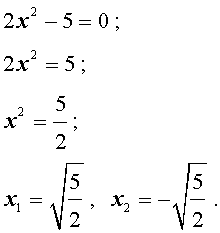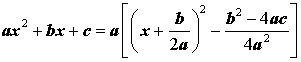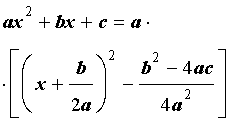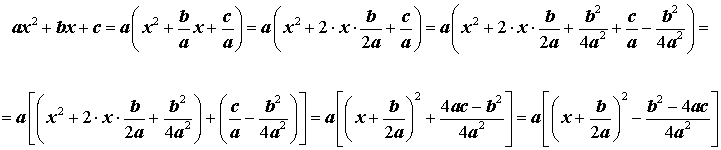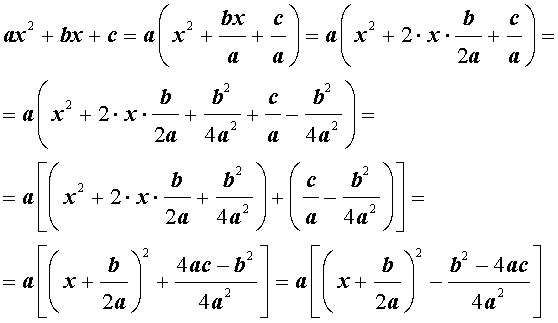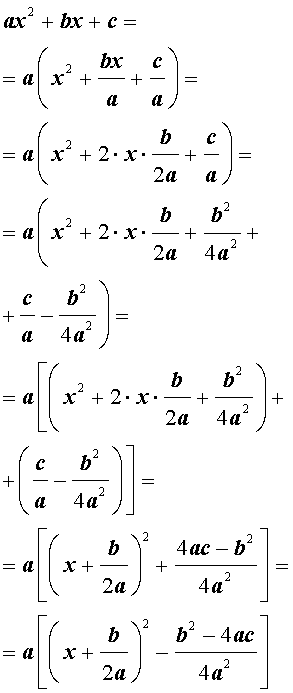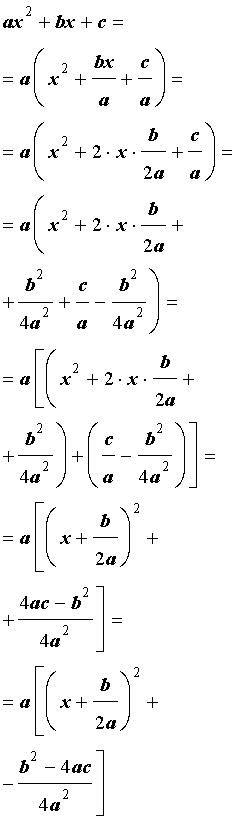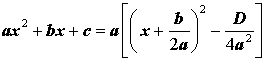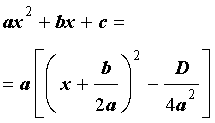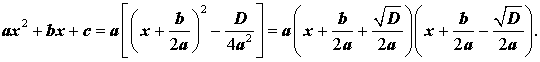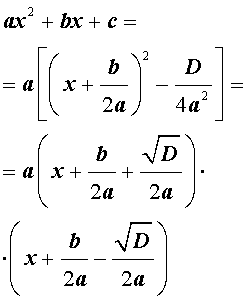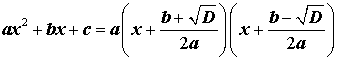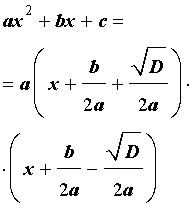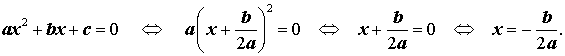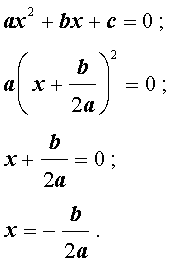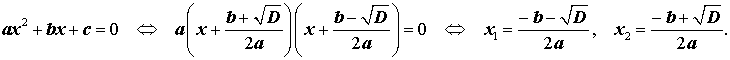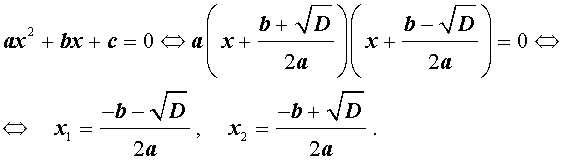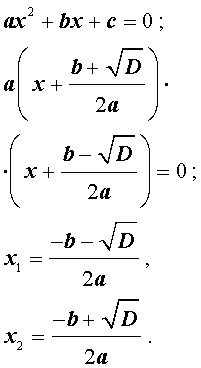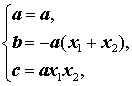Задача выделения полного квадрата заключается в преобразовании квадратного многочлена следующим образом:
где и неизвестные параметры которые требуется определить.
Для определения неизвестных параметров и , преобразуем приведенное выше равенство следующим образом:
и далее, раскроем скобки:
Для того, чтобы приведённое выше равенство соблюдалось, приравняем коэффициенты при одинаковых степенях:
В полученной системе уравнений, первое уравнение обозначает верное тождество при любых значениях параметра , поэтому его можно исключить. Из второго уравнения выражаем параметр и подставляем полученное выражение в третье уравнение системы:
Упрощаем третье уравнение системы и выражением из него значение параметра :
Подставляем полученные значения и в самое первое уравнение и получаем формулу для выделения полного квадрата из квадратного многочлена:
Необходимость выделения полного квадрата часто возникает при решении задач интегрирования рациональных функций. Кроме того, выделив полный квадрат, можно получить формулу для решения квадратных уравнений.
Наш онлайн калькулятор выделяет полный квадрат для многочлена второй степени с описанием подробного хода решения на русском языке.
- Квадратные уравнения
- Решение неполных квадратных уравнений
- Выделение полного квадрата
- Дискриминант
- Разложение квадратного трёхчлена на множители
- Формула для корней квадратного уравнения
- Прямая и обратная теоремы Виета
- Выделение полного квадрата из уравнения
- §2. Выделение полного квадрата из квадратного трёхчлена
- 📸 Видео
Видео:Математика - Выделение полного квадратаСкачать

Квадратные уравнения
 Решение неполных квадратных уравнений Решение неполных квадратных уравнений |
 Выделение полного квадрата Выделение полного квадрата |
 Дискриминант Дискриминант |
 Разложение квадратного трехчлена на множители Разложение квадратного трехчлена на множители |
 Формула для корней квадратного уравнения Формула для корней квадратного уравнения |
 Прямая и обратная теоремы Виета Прямая и обратная теоремы Виета |
Квадратным трёхчленом относительно переменной x называют многочлен
| ax 2 + bx + c , | (1) |
где a, b и c – произвольные вещественные числа, причем
Квадратным уравнением относительно переменной x называют уравнение
| ax 2 + bx + c = 0, | (2) |
где a, b и c – произвольные вещественные числа, причем
Полным квадратным уравнением относительно переменной x называют уравнение
где a, b и c – произвольные вещественные числа, отличные от нуля.
Неполными квадратными уравнениями называют квадратные уравнения следующих типов:
 | 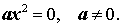 |
 | 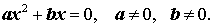 |
 | 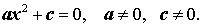 |
Видео:Полный квадрат. Где и когда он может пригодиться? | Математика TutorOnlineСкачать

Решение неполных квадратных уравнений
Покажем, как решаются неполные квадратные уравнения на примерах.
Пример 1 . Решить уравнение
Пример 2 . Решить уравнение
| 2x 2 + 3x= 0 . | (3) |
Решение . Вынося в левой части уравнения (3) переменную x за скобки, перепишем уравнение в виде
| x (2x+ 3) = 0 . | (4) |
Поскольку произведение двух сомножителей равно нулю тогда и только тогда, когда, или первый сомножитель равен нулю, или второй сомножитель равен нулю, то из уравнения (4) получаем:
Ответ : 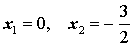
Пример 3 . Решить уравнение
Ответ : 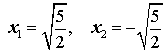
Пример 4 . Решить уравнение
| 3x 2 + 11 = 0 . | (5) |
Решение . Поскольку левая часть уравнения (5) положительна при всех значениях переменной x , а правая часть равна 0, то уравнение решений не имеет.
Ответ : 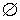
Видео:Метод выделения полного квадрата. 8 класс.Скачать

Выделение полного квадрата
Выделением полного квадрата называют представление квадратного трёхчлена (1) в виде:
Для того, чтобы получить формулу (6), совершим следующие преобразования:
Формула (6) получена.
Видео:2017-02-13 Алгебра 7 класс. Выделение полного квадрата.Скачать

Дискриминант
Дискриминантом квадратного трёхчлена (1) называют число, которое обозначается буквой D и вычисляется по формуле:
| D = b 2 – 4ac. | (7) |
Дискриминант квадратного трёхчлена играет важную роль, и от того, какой знак он имеет, зависят различные свойства квадратного трёхчлена.
Используя дискриминант, формулу (6) можно переписать в виде
Видео:7 класс, 25 урок, Метод выделения полного квадратаСкачать

Разложение квадратного трёхчлена на множители
Утверждение . В случае, когда 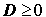
Доказательство . В случае, когда D = 0 , формула (8) и является разложением квадратного трехчлена на линейные множители:
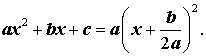 | (9) |
В случае, когда D > 0 , выражение, стоящее в квадратных скобках в формуле (8), можно разложить на множители, воспользовавшись формулой сокращенного умножения «Разность квадратов»:
Таким образом, в случае, когда D > 0 , разложение квадратного трехчлена (1) на линейные множители имеет вид
В случае, когда D , выражение, стоящее в квадратных скобках в формуле (8), является суммой квадратов и квадратный трёхчлен на множители не раскладывается.
Замечание . В случае, когда D , квадратный трехчлен всё-таки можно разложить на линейные множители, но только в области комплексных чисел, однако этот материал выходит за рамки школьного курса.
Видео:Алгебра 7 класс (Урок№28 - Выделение полного квадрата.)Скачать

Формула для корней квадратного уравнения
Из формул (9) и (10) вытекает формула для корней квадратного уравнения .
Действительно, в случае, когда D = 0 , из формулы (9) получаем:
Следовательно, в случае, когда D = 0 , уравнение (1) обладает единственным корнем, который вычисляется по формуле
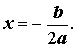 | (11) |
В случае, когда D > 0 , из формулы (10) получаем:
Таким образом, в случае, когда D > 0 , уравнение (1) имеет два различных корня , которые вычисляются по формулам
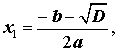 | (12) |
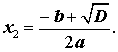 | (13) |
Замечание 1 . Формулы (12) и (13) часто объединяют в одну формулу и записывают так:
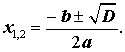 | (14) |
Замечание 2 . В случае, когда D = 0 , обе формулы (12) и (13) превращаются в формулу (11). Поэтому часто говорят, что в случае, когда D = 0 , квадратное уравнение (1) имеет два совпавших корня , вычисляемых по формуле (11), а саму формулу (11) переписывают в виде:
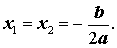 | (15) |
Замечание 3 . В соответствии с материалом, изложенным в разделе «Кратные корни многочленов», корень (11) является корнем уравнения (1) кратности 2.
В случае, когда D = 0 , разложение квадратного трехчлена на линейные множители (9) можно переписать по-другому, воспользовавшись формулой (15):
| ax 2 + bx + c = = a (x – x1) 2 . | (16) |
В случае, когда D > 0 , разложение квадратного трехчлена на линейные множители (10) с помощью формул (12) и (13) переписывается так:
| ax 2 + bx + c = = a (x – x1) (x – x2) . | (17) |
Замечание 4 . В случае, когда D = 0 , корни x1 и x2 совпадают, и формула (17) принимает вид (16).
Видео:Метод выделения полного квадрата / Как решать квадратные уравнения?Скачать

Прямая и обратная теоремы Виета
Раскрывая скобки и приводя подобные члены в правой части формулы (17), получаем равенство
Отсюда, поскольку формула (17) является тождеством, вытекает, что коэффициенты многочлена
равны соответствующим коэффициентам многочлена
Таким образом, справедливы равенства
следствием которых являются формулы
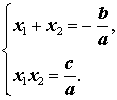 | (18) |
Формулы (18) и составляют содержание теоремы Виета (прямой теоремы Виета) .
Словами прямая теорема Виета формулируется так: — «Если числа x1 и x2 являются корнями квадратного уравнения (1), то они удовлетворяют равенствам (18)».
Обратная теорема Виета формулируется так: — «Если числа x1 и x2 являются решениями системы уравнений (18), то они являются корнями квадратного уравнения (1)».
Для желающих ознакомиться с примерами решений различных задач по теме «Квадратные уравнения» мы рекомендуем наше учебное пособие «Квадратный трехчлен».
Графики парабол и решение с их помощью квадратных неравенств представлены в разделе «Парабола на координатной плоскости. Решение квадратных неравенств» нашего справочника.
Видео:Математика Без Ху!ни. Метод выделения полного квадрата.Скачать

Выделение полного квадрата из уравнения
Описание метода выделения полного квадрата
§2. Выделение полного квадрата из квадратного трёхчлена
Описание метода выделения полного квадрата
Выражения вида 2 x 2 + 3 x + 5 , `-4x^2+5x+7` носят название квадратного трёхчлена. В общем случае квадратным трёхчленом называют выражение вида a x 2 + b x + c , где a , b , c a, b, c – произвольные числа, причём a ≠ 0 .
Рассмотрим квадратный трёхчлен x 2 — 4 x + 5 . Запишем его в таком виде: x 2 — 2 · 2 · x + 5 . Прибавим к этому выражению 2 2 и вычтем 2 2 , получаем: x 2 — 2 · 2 · x + 2 2 — 2 2 + 5 . Заметим, что x 2 — 2 · 2 · x + 2 2 = ( x — 2 ) 2 , поэтому
x 2 — 4 x + 5 = ( x — 2 ) 2 — 4 + 5 = ( x — 2 ) 2 + 1 .
Преобразование, которое мы сделали, носит название «выделение полного квадрата из квадратного трёхчлена».
Выделите полный квадрат из квадратного трёхчлена 9 x 2 + 3 x + 1 .
Заметим, что 9 x 2 = ( 3 x ) 2 , `3x=2*1/2*3x`. Тогда
Прибавим и вычтем к полученному выражению `(1/2)^2`, получаем
Покажем, как применяется метод выделения полного квадрата из квадратного трёхчлена для разложения квадратного трёхчлена на множители.
Разложите на множители квадратный трёхчлен 4 x 2 — 12 x + 5 .
Выделяем полный квадрат из квадратного трёхчлена:
2 x 2 — 2 · 2 x · 3 + 3 2 — 3 2 + 5 = 2 x — 3 2 — 4 = ( 2 x — 3 ) 2 — 2 2 .
Теперь применяем формулу a 2 — b 2 = ( a — b ) ( a + b ) , получаем:
( 2 x — 3 — 2 ) ( 2 x — 3 + 2 ) = ( 2 x — 5 ) ( 2 x — 1 ) .
Разложите на множители квадратный трёхчлен — 9 x 2 + 12 x + 5 .
— 9 x 2 + 12 x + 5 = — 9 x 2 — 12 x + 5 . Теперь замечаем, что 9 x 2 = 3 x 2 , — 12 x = — 2 · 3 x · 2 .
Прибавляем к выражению 9 x 2 — 12 x слагаемое 2 2 , получаем:
— 3 x 2 — 2 · 3 x · 2 + 2 2 — 2 2 + 5 = — 3 x — 2 2 — 4 + 5 = — 3 x — 2 2 + 4 + 5 = = — 3 x — 2 2 + 9 = 3 2 — 3 x — 2 2 .
Применяем формулу для разности квадратов, имеем:
— 9 x 2 + 12 x + 5 = 3 — 3 x — 2 3 + ( 3 x — 2 ) = ( 5 — 3 x ) ( 3 x + 1 ) .
Разложите на множители квадратный трёхчлен 3 x 2 — 14 x — 5 .
Мы не можем представить выражение 3 x 2 как квадрат какого-то выражения, т. к. ещё не изучали этого в школе. Это будете проходить позже, и уже в Задании №4 будем изучать квадратные корни. Покажем, как можно разложить на множители заданный квадратный трёхчлен:
Покажем, как применяется метод выделения полного квадрата для нахождения наибольшего или наименьшего значений квадратного трёхчлена.
Рассмотрим квадратный трёхчлен x 2 — x + 3 . Выделяем полный квадрат:
`(x)^2-2*x*1/2+(1/2)^2-(1/2)^2+3=(x-1/2)^2+11/4`. Заметим, что при `x=1/2` значение квадратного трёхчлена равно `11/4`, а при `x!=1/2` к значению `11/4` добавляется положительное число, поэтому получаем число, большее `11/4`. Таким образом, наименьшее значение квадратного трёхчлена равно `11/4` и оно получается при `x=1/2`.
Найдите наибольшее значение квадратного трёхчлена — 16 x 2 + 8 x + 6 .
Выделяем полный квадрат из квадратного трёхчлена: — 16 x 2 + 8 x + 6 = — 4 x 2 — 2 · 4 x · 1 + 1 — 1 + 6 = — 4 x — 1 2 — 1 + 6 = = — 4 x — 1 2 + 7 .
При `x=1/4` значение квадратного трёхчлена равно 7 , а при `x!=1/4` из числа 7 вычитается положительное число, то есть получаем число, меньшее 7 . Таким образом, число 7 является наибольшим значением квадратного трёхчлена, и оно получается при `x=1/4`.
Разложите на множители числитель и знаменатель дроби `/` и сократите эту дробь.
Заметим, что знаменатель дроби x 2 — 6 x + 9 = x — 3 2 . Разложим числитель дроби на множители, применяя метод выделения полного квадрата из квадратного трёхчлена.
x 2 + 2 x — 15 = x 2 + 2 · x · 1 + 1 — 1 — 15 = x + 1 2 — 16 = x + 1 2 — 4 2 = = ( x + 1 + 4 ) ( x + 1 — 4 ) = ( x + 5 ) ( x — 3 ) .
Данную дробь привели к виду `/(x-3)^2` после сокращения на ( x — 3 ) получаем `(x+5)/(x-3)`.
Разложите многочлен x 4 — 13 x 2 + 36 на множители.
Применим к этому многочлену метод выделения полного квадрата.
Разложите на множители многочлен 4 x 2 + 4 x y — 3 y 2 .
Применяем метод выделения полного квадрата. Имеем:
( 2 x ) 2 + 2 · 2 x · y + y 2 — y 2 — 3 y 2 = ( 2 x + y ) 2 — 2 y 2 = = ( 2 x + y + 2 y ) ( 2 x + y — 2 y ) = ( 2 x + 3 y ) ( 2 x — y ) .
Применяя метод выделения полного квадрата, разложите на множители числитель и знаменатель и сократите дробь `/`.
📸 Видео
Выделение полного квадратаСкачать

ВЫДЕЛЕНИЕ ПОЛНОГО КВАДРАТА 8 классСкачать

8 класс. Метод выделения полного квадрата. Алгебра.Скачать

Как избавиться от двойного корня с помощью выделения полного квадратаСкачать

Алгебра 8 класс Метод выделения полного квадратаСкачать

Выделение полного квадрата. Решение уравненийСкачать

Метод выделения полного квадрата | Квадратные уравненияСкачать

Видеоурок "Выделение полного квадрата"Скачать

Выделение полного квадратаСкачать

Математика| Разложение квадратного трехчлена на множители.Скачать

Решение уравнения методом выделения полного квадратаСкачать

Решаем квадратные уравнения, как?.. Метод выделения полного квадратаСкачать