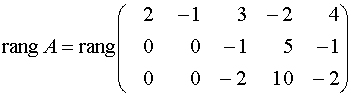Вычислите сумму рангов основной и расширенной матриц системы уравнений

Назначение сервиса . Онлайн-калькулятор предназначен для нахождения ранга матрицы. При этом решение сохраняется в формате Word и Excel . см. пример решения.

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word

Определение . Пусть дана матрица ранга r . Любой минор матрицы, отличный от нуля и имеющий порядок r, называется базисным, а строки и столбцы его составляющие – базисными строками и столбцами.
Согласно этому определению, матрица A может иметь несколько базисных миноров.

Ранг единичной матрицы E равен n (количеству строк).

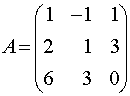
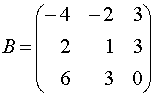
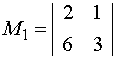
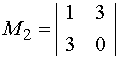
Пример 1 . Даны две матрицы , и их миноры , . Какой из них можно принять в качестве базисного?
Решение. Минор M₁=0, поэтому он не может быть базисным ни для одной из матриц. Минор M₂=-9≠0 и имеет порядок 2, значит его можно принять в качестве базисного матриц A или / и B при условии, что они имеют ранги, равные 2 . Поскольку detB=0 (как определитель с двумя пропорциональными столбцами), то rangB=2 и M₂ можно взять за базисный минор матрицы B. Ранг матрицы A равен 3, в силу того, что detA=-27≠0 и, следовательно, порядок базисного минора этой матрицы должен равняться 3, то есть M₂ не является базисным для матрицы A . Отметим, что у матрицы A единственный базисный минор, равный определителю матрицы A .

Теорема (о базисном миноре). Любая строка (столбец) матрицы является линейной комбинацией ее базисных строк (столбцов).
Следствия из теоремы.

1. Всякие (r+1) столбцов (строк) матрицы ранга r линейно зависимы.
2. Если ранг матрицы меньше числа ее строк (столбцов), то ее строки (столбцы) линейно зависимы. Если rangA равен числу ее строк (столбцов), то строки (столбцы) линейно независимы.
3. Определитель матрицы A равен нулю тогда и только тогда, когда ее строки (столбцы) линейно зависимы.
4. Если к строке (столбцу) матрицы прибавить другую строку, (столбец) умноженную на любое число, отличное от нуля, то ранг матрицы не изменится.
5. Если в матрице зачеркнуть строку (столбец), являющуюся линейной комбинацией других строк (столбцов), то ранг матрицы не изменится.
6. Ранг матрицы равен максимальному числу ее линейно независимых строк (столбцов).
7. Максимальное число линейно независимых строк совпадает с максимальным числом линейно независимых столбцов.

Пример 2 . Найти ранг матрицы .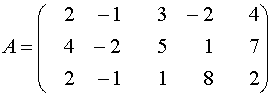
Решение. Исходя из определения ранга матрицы, будем искать минор наивысшего порядка, отличный от нуля. Сначала преобразуем матрицу к более простому виду. Для этого первую строку матрицы умножим на (-2) и прибавим ко второй, затем ее же умножим на (-1) и прибавим к третьей:

Пример 3 . Привести данную матрицу к ступенчатому виду и определить её ранг. .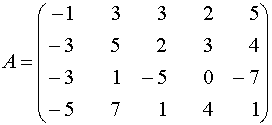
Решение. Получим нули в первом столбце, оперируя первой строкой .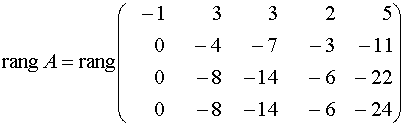
Третью строку вычеркиваем, поскольку она получается умножением второй строки на 2, а в последней строке отбросим общий множитель:

Видео:11. Ранг матрицыСкачать

Онлайн калькулятор. Ранг матрицы

Используя этот онлайн калькулятор для вычисления ранга матрицы, вы сможете очень просто и быстро найти ранг матрицы.

Воспользовавшись онлайн калькулятором для вычисления ранга матрицы, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисления ранга матрицы, а также закрепить пройденный материал.

Видео:Ранг матрицыСкачать

Найти ранг матрицы

Ввод данных в калькулятор ранга матриц

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора ранга матриц

• Между полями для ввода можно перемещаться нажимая клавиши , , и на клавиатуре.

Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Теория. Ранг матриц.

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:Ранг матрицыСкачать

Метод Гаусса онлайн

Данный онлайн калькулятор находит решение системы линейных уравнений (СЛУ) методом Гаусса. Дается подробное решение. Для вычисления выбирайте количество переменных и количество уравнений. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить.»

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Видео:Решение системы уравнений методом ГауссаСкачать

Метод Гаусса

Метод Гаусса − это метод перехода от исходной системы линейных уравнений (при помощи эквивалентных преобразований) к системе, которая решается проще, чем исходная система.

Эквивалентными преобразованиями системы линейных уравнений являются:

• перемена местами двух уравнений в системе,
• умножение какого-либо уравнения в системе на ненулевое действительное число,
• прибавление к одному уравнению другого уравнения, умноженного на произвольное число.

Рассмотрим систему линейных уравнений:

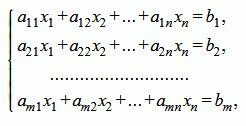(1)

Запишем систему (1) в матричном виде:

(3)

A-называется матрица коэффициентов системы, b − правая часть ограничений, x− вектор переменных, которую нужно найти. Пусть rang(A)=p.

Эквивалентные преобразования не меняют ранг матрицы коэффициентов и ранг расширеннной матрицы системы. Не меняется также множество решений системы при эквивалентных преобразованиях. Суть метода Гаусса заключается в приведении матрцы коэффициентов A к диагональному или ступенчатому.

Построим расшренную матрицу системы:

(4)

Предположим a₁₁≠0. Если это не так, то можно поменять местами эту строку со строкой с ненулевым элементом в столбце 1 (если нет таких строк, то переходим к следующему столбцу). Обнуляем все элементы столбца 1 ниже ведущего элемента a₁₁. Для этого сложим строки 2,3, . m со строкой 1, умноженной на −a₂₁/a₁₁, −a₃₁/a₁₁, . −a_m1/a₁₁, соответственно. Тогда (4) примет следующий вид:

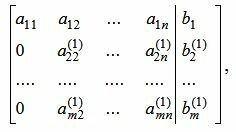(5)

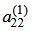
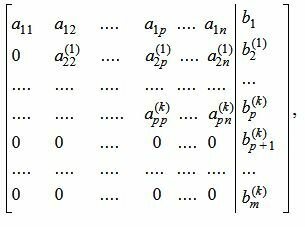На следующем этапе обнуляем все элементы столбца 2, ниже элемента . Если данный элемент нулевой, то эту строку меняем местами со строкой, лежащий ниже данной строки и имеющий ненулевой элемент во втором столбце. Далее обнуляем все элементы столбца 2 ниже ведущего элемента a₂₂. Для этого сложим строки 3, . m со строкой 2, умноженной на −a₃₂/a₂₂, . −a_m2/a₂₂, соответственно. Продолжая процедуру, получим матрицу диагонального или ступенчатого вида. Пусть полученная расширенная матрица имеет вид:

(6)

Обратим внимание на последние строки. Если 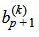. равны нулю, то система линейных уравнений имеет решение, если же хотя бы один из этих чисел отлично от нуля, то система несовместна. Иными словами, система (2) совместна тогда и только тогда, когда ранг матрицы A навен рангу расширенной матрицы (A|b).

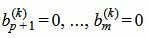
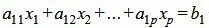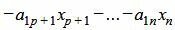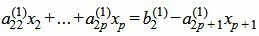Пусть . Тогда

(7)

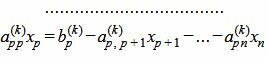Так как rangA=rang(A|b), то множество решений (7) есть (n−p)− многообразие. Следовательно n−p неизвестных можно выбрать произвольно. Остальные неизвестные из системы (7) вычисляются так. Из последнего уравнения выражаем x_p через остальные переменные и вставляем в предыдущие выражения. Далее из предпоследнего уравнения выражаем x_p−1 через остальные переменные и вставляем в предыдущие выражения и т.д. Рассмотрим метод Гаусса на конкретных примерах.

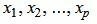
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Примеры решения системы линейных уравнений методом Гаусса

Пример 1. Найти общее решение системы линейных уравнений методом Гаусса:

Матричный вид записи: Ax=b, где

Для решения системы, запишем расширенную матрицу:

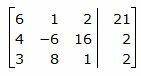Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Исключим элементы 1-го столбца матрицы ниже элемента a_{1 1}. Для этого сложим строки 2,3 со строкой 1, умноженной на -2/3,-1/2 соответственно:

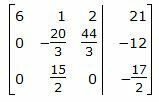Исключим элементы 2-го столбца матрицы ниже элемента a2 2. Для этого сложим строку 3 со строкой 2, умноженной на 9/8:

Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

Из вышеизложенной таблицы можно записать:

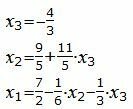Подставив верхние выражения в нижние, получим решение.

,,.

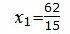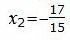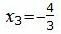Пример 2. Найти общее решение системы линейных уравнений методом Гаусса:

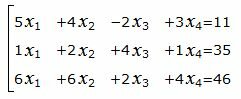Матричный вид записи: Ax=b, где

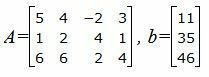Для решения системы, построим расширенную матрицу:

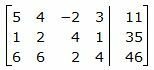Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Исключим элементы 1-го столбца матрицы ниже элемента a₁₁. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/5,-6/5 соответственно:

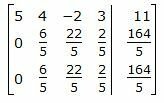Исключим элементы 2-го столбца матрицы ниже элемента a₂₂. Для этого сложим строку 3 со строкой 2, умноженной на -1:

Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

Выразим переменные x₁, x₂ относительно остальных переменных.

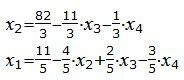где x₃, x₄− произвольные действительные числа.

Подставив верхние выражения в нижние, получим решение.

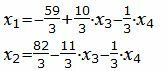где x₃, x₄− произвольные действительные числа.

Векторный вариант решения:

Запишем вышеизложенное решение, представив свободные переменные в виде тождеств:

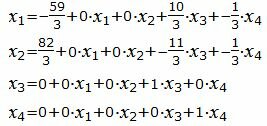Тогда векторное решение можно представить так:

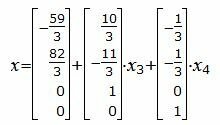где x₃, x₄− произвольные действительные числа.

🎥 Видео

Как найти ранг матрицы (пример) - bezbotvyСкачать

Матричный метод решения систем уравненийСкачать

Как найти ранг матрицы Три способа Разбор на конкретных примерахСкачать

Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать

12. Метод Гаусса решения систем линейных уравнений. Часть 1.Скачать

Математика без Ху!ни. Метод Гаусса.Скачать

Линейная алгебра, 6 урок, Ранг матрицыСкачать

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Лекция 11.2. Ранг матрицы. Метод окаймляющих миноровСкачать

Найти ранг матрицы при всех значениях параметраСкачать

9. Вычисление ранга методом окаймляющих миноровСкачать

Лекция 13. Исследование систем линейных уравнений. Теорема Кронекера — Капелли.Скачать