Вычислите определитель матрицы системы 2x 4y 1 3x 5y 2 решение уравнения (3 видео)

Определитель матрицы онлайн

Данный онлайн калькулятор вычисляет определитель матрицы. Дается подробное решение. Для вычисления определителя матрицы выбирайте порядок (размер) квадратной матрицы. Введите данные в ячейки. Выберите метод решения и нажмите на кнопку «Вычислить». Теоретическую часть смотрите на странице определитель матрицы.

Содержание

Предупреждение
Примеры вычисления определителя матрицы
Вычислите определитель матрицы системы 2x 4y 1 3x 5y 2 решение уравнения
Определение
Где учитесь?
Определитель матрицы онлайн
Описание калькулятора определителя матрицы
Решение задач по математике онлайн
Калькулятор онлайн. Решение системы двух линейных уравнений с двумя переменными. Метод подстановки и сложения.
Немного теории.
Решение систем линейных уравнений. Способ подстановки
Решение систем линейных уравнений способом сложения
💡 Видео

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Видео:Решение системы уравнений методом Крамера 2x2Скачать

Примеры вычисления определителя матрицы

Пример 1. Найти определитель матрицы

Вычислите определитель матрицы системы 2x 4y 1 3x 5y 2 решение уравнения

Для вычисления определителя матрицы, приведем матрицу к верхнему треугольному виду.

Выбираем самый большой по модулю ведущий элемент столбца 1. Для этого меняем местами строки 1 и 2. При этом меняется знак определителя на «−»:

Исключим элементы 1-го столбца матрицы ниже главной диагонали. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/78,-2/78 соответственно:

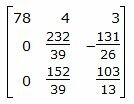Исключим элементы 2-го столбца матрицы ниже главной диагонали. Для этого сложим строку 3 со строкой 2, умноженной на -5928/9048:

Мы привели матрицу к верхнему треугольному виду. Определитель матрицы равен произведению всех элементов главной диагонали (учитывая знак определителя):

Пример 2. Найти определитель матрицы A, разложением определителя по первой строке:

Для вычисления определителя матрицы методом разложения по первой строке, вычисляем произведение каждого элемента первой строки на соответствующее алгебраическое дополнение и суммируем полученные результаты:

Видео:Как вычислить определитель матрицы четвертого порядка | Высшая математикаСкачать

Вычислите определитель матрицы системы 2x 4y 1 3x 5y 2 решение уравнения

Вы получите подробное решение по нахождению определителя матрицы.
Вычислим определитель det(A) для матрицы A.

Определение

Определение детерминанта матрицы выглядит следующим образом:

Определитель матрицы — это сумма произведений минус единицы в степени числа инверсий в перестановке умноженное два раза на два разных элемента соотв. матрицы с индексами, которые составляют перестановку чисел от 1 до «размера матрицы»

Видео:Найти определитель матрицы 4x4Скачать

Где учитесь?

Для правильного составления решения, укажите:

Видео:Как решить уравнение с определителем | Высшая математикаСкачать

Определитель матрицы онлайн

Вычислить определитель матрицы онлайн можно различными способами с помощью нашего сервиса. Решение бесплатное с пошаговыми действиями и пояснениями.

Определитель матрицы – это сумма слагаемых всевозможных произведений элементов матрицы, взятых по одному из каждой строки и каждого столбца матрицы, при этом знак произведения определяется четностью перестановки.

Видео:5 способов вычисления определителя ★ Какой способ лучше?Скачать

Описание калькулятора определителя матрицы

Данный калькулятор поможет научиться находить определитель матрицы различными способами:

используя метод Гаусса
с помощью Правила треугольников
по Правилу Саррюса
с использованием формулы Лейбница
методом Гаусса-Монтанте (алгоритм Барейса)

Наш сервис не только позволяет получить определитель матицы, но и предоставляет последовательность решения с комментариями и пояснениями в режиме онлайн, бесплатно. Так же калькулятор может быть полезен при проверке правильности выполненного самостоятельно решения.

Заполните поля для элементов матрицы и нажмите соответствующую кнопку.

С помощью плюса и минуса выберите нужный размер матрицы. Если нужна неквадратная матрица, то просто ненужные ячейки оставьте пустыми.
Внесите значение элементов матрицы в ячейки. Значения могут быть:
- целые числа: 7 , -3 , 0
- десятичные (конечные и периодические) дроби: 7/8 , 6.13 , -1.3(56) , 1.2e-4
- арифметические выражения: 1/2+3*(6-4) , (6-y)/x^3 , 2^0.5
Нажмите на кнопку с названием нужной математической операции.
Значения в результатах решения можно с помощью мышки перетаскивать на различные поля. Например, полученную матрицу можно перетащить на поле исходных данных, для дальнейшего решения.

Видео:Решение системы уравнений методом Крамера 4x4Скачать

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Видео:Решение системы уравнений методом Крамера.Скачать

Калькулятор онлайн.
Решение системы двух линейных уравнений с двумя переменными.
Метод подстановки и сложения.

С помощью данной математической программы вы можете решить систему двух линейных уравнений с двумя переменными методом подстановки и методом сложения.

Программа не только даёт ответ задачи, но и приводит подробное решение с пояснениями шагов решения двумя способами: методом подстановки и методом сложения.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

В качестве переменной может выступать любая латинсая буква.
Например: ( x, y, z, a, b, c, o, p, q ) и т.д.

При вводе уравнений можно использовать скобки. При этом уравнения сначала упрощаются. Уравнения после упрощений должны быть линейными, т.е. вида ax+by+c=0 с точностью порядка следования элементов.
Например: 6x+1 = 5(x+y)+2

В уравнениях можно использовать не только целые, но также и дробные числа в виде десятичных и обыкновенных дробей.

Правила ввода десятичных дробей.
Целая и дробная часть в десятичных дробях может разделяться как точкой так и запятой.
Например: 2.1n + 3,5m = 55

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Целая часть отделяется от дроби знаком амперсанд: &

Примеры.
-1&2/3y + 5/3x = 55
2.1p + 55 = -2/7(3,5p — 2&1/8q)

Решить систему уравнений

Видео:Как найти определитель матрицы 2х2, 3х3 и 4х4Скачать

Немного теории.

Видео:Как вычислить определитель второго порядка | Высшая математикаСкачать

Решение систем линейных уравнений. Способ подстановки

Последовательность действий при решении системы линейных уравнений способом подстановки:
1) выражают из какого-нибудь уравнения системы одну переменную через другую;
2) подставляют в другое уравнение системы вместо этой переменной полученное выражение;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующее значение второй переменной.

Пример. Решим систему уравнений:
$$ left< begin 3x+y=7 \ -5x+2y=3 end right. $$

Выразим из первого уравнения y через x: y = 7-3x. Подставив во второе уравнение вместо y выражение 7-Зx, получим систему:
$$ left< begin y = 7—3x \ -5x+2(7-3x)=3 end right. $$

Нетрудно показать, что первая и вторая системы имеют одни и те же решения. Во второй системе второе уравнение содержит только одну переменную. Решим это уравнение:
$$ -5x+2(7-3x)=3 Rightarrow -5x+14-6x=3 Rightarrow -11x=-11 Rightarrow x=1 $$

Подставив в равенство y=7-3x вместо x число 1, найдем соответствующее значение y:
$$ y=7-3 cdot 1 Rightarrow y=4 $$

Пара (1;4) — решение системы

Системы уравнений с двумя переменными, имеющие одни и те же решения, называются равносильными. Системы, не имеющие решений, также считают равносильными.

Видео:Решение системы уравнений методом Гаусса 4x4Скачать

Решение систем линейных уравнений способом сложения

Рассмотрим еще один способ решения систем линейных уравнений — способ сложения. При решении систем этим способом, как и при решении способом подстановки, мы переходим от данной системы к другой, равносильной ей системе, в которой одно из уравнений содержит только одну переменную.

Последовательность действий при решении системы линейных уравнений способом сложения:
1) умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами;
2) складывают почленно левые и правые части уравнений системы;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующее значение второй переменной.

Пример. Решим систему уравнений:
$$ left< begin 2x+3y=-5 \ x-3y=38 end right. $$

В уравнениях этой системы коэффициенты при y являются противоположными числами. Сложив почленно левые и правые части уравнений, получим уравнение с одной переменной 3x=33. Заменим одно из уравнений системы, например первое, уравнением 3x=33. Получим систему
$$ left< begin 3x=33 \ x-3y=38 end right. $$

Из уравнения 3x=33 находим, что x=11. Подставив это значение x в уравнение ( x-3y=38 ) получим уравнение с переменной y: ( 11-3y=38 ). Решим это уравнение:
( -3y=27 Rightarrow y=-9 )

Таким образом мы нашли решение системмы уравнений способом сложения: ( x=11; y=-9 ) или ( (11; -9) )

Воспользовавшись тем, что в уравнениях системы коэффициенты при y являются противоположными числами, мы свели ее решение к решению равносильной системы (сумировав обе части каждого из уравнений исходной симтемы), в которой одно из уравнений содержит только одну переменную.