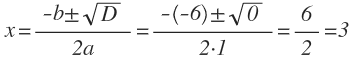Вычислите дискриминант квадратного уравнения по формуле d b 4ac (6 видео)

Решить квадратное уравнение онлайн

На данной странице калькулятор онлайн помоежет решить квадратное уравнение. При решении выводится описание.

Квадратное уравнение — это уравнение вида ax 2 +bx+c=0 , где a не равно 0 .

Содержание

Через дискриминант
Как найти дискриминант квадратного уравнения
Понятие квадратного уравнения
Понятие дискриминанта
Как решать квадратные уравнения через дискриминант
Примеры решения квадратных уравнений с помощью дискриминанта
Дискриминант квадратного уравнения
Решение квадратных уравнений через дискриминант
📽️ Видео

Через дискриминант

a x 2 + b x + c = 0

Что бы решить квадратное уравнение, нужно найти все x . При подстановке должно выполняться равенство
ax 2 + bx + c = 0 .

Для начала находится дискриминант по формуле D = b 2 — 4ac :

Если D > 0 , уравнение имеет два корня.
Если D = 0 , уравнение имеет один корень.
Если D > 0 , уравнение не имеет корней.

Корни квадратного уравнения находятся по формуле:

Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Как найти дискриминант квадратного уравнения

О чем эта статья:

Видео:РАЗБИРАЕМ ДИСКРИМИНАНТ ЧАСТЬ I #shorts #математика #егэ #огэ #дискриминантСкачать

Понятие квадратного уравнения

Уравнение — это равенство, содержащее переменную, значение которой нужно найти.

Например, х + 8 = 12 — это уравнение, содержащее переменную х.

Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.

Например, если х = 5, то при подстановке в уравнение мы получим:

13 = 12 — противоречие.

Значит, х = 5 не является корнем уравнения.

Если же х = 4, то при подстановке в уравнение мы получим:

12 = 12 — верное равенство.

Значит, х = 4 является корнем уравнения.

Решить уравнение — значит найти все его корни или доказать, что их не существует.

Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Если все коэффициенты в уравнении отличны от нуля, то уравнение называется полным.

Такое уравнение можно решить с помощью формулы дискриминанта.

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Понятие дискриминанта

Дискриминант квадратного уравнения — это выражение, равное b 2 − 4ac. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.

Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.

Видео:Как решать квадратные уравнения через дискриминант. Простое объяснениеСкачать

Как решать квадратные уравнения через дискриминант

Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:

Определим, чему равны коэффициенты a, b, c.

Вычислим значение дискриминанта по формуле D = b2 − 4ac.

Если дискриминант D 0, то у уравнения две корня, равные

Чтобы запомнить алгоритм решения полных квадратных уравнений и с легкостью его использовать, сохраните себе шпаргалку:

Видео:Квадратное уравнение, дискриминант, формула корнейСкачать

Примеры решения квадратных уравнений с помощью дискриминанта

Пример 1. Решить уравнение: 3x 2 — 4x + 2 = 0.

Определим коэффициенты: a = 3, b = -4, c = 2.
Найдем дискриминант: D = b 2 — 4ac = (-4) 2 — 4 * 3 * 2 = 16 — 24 = -8.

Ответ: D 2 — 6x + 9 = 0.

Определим коэффициенты: a = 1, b = -6, c = 9.
Найдем дискриминант: D = b 2 — 4ac = (-6) 2 — 4 * 1 * 9 = 36 — 36 = 0.

D = 0, значит уравнение имеет один корень:

Ответ: корень уравнения 3.

Пример 3. Решить уравнение: x 2 — 4x — 5 = 0.

Определим коэффициенты: a = 1, b = -4, c = -5.
Найдем дискриминант: D = b 2 — 4ac = (-4) 2 — 4 * 1 * (-5) = 16 + 20 = 36.

D > 0, значит уравнение имеет два корня:

Ответ: два корня x₁ = 5, x₂ = -1.

Разобраться в решении квадратных уравнений на практике с классным преподавателем можно на курсах по математике в Skysmart.

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Дискриминант квадратного уравнения

Дискриминант квадратного уравнения — это выражение, находящееся под корнем в формуле нахождения корней квадратного уравнения. Дискриминант обозначается латинской буквой D.

Вид уравнения	Формула корней	Формула дискриминанта
ax 2 + bx + c = 0		b 2 — 4ac
ax 2 + 2kx + c = 0		k 2 — ac
x 2 + px + q = 0
x 2 + px + q = 0		p 2 — 4q

Все формулы нахождения корней квадратных уравнений можно записать короче с помощью дискриминанта:

Вид уравнения	Формула
ax 2 + bx + c = 0	, где D = b 2 — 4ac
ax 2 + 2kx + c = 0	, где D = k 2 — ac
x 2 + px + q = 0	, где D =
x 2 + px + q = 0	, где D = p 2 — 4q

Дискриминант позволяет определить, имеет ли уравнение корни и сколько их, не решая само уравнение:

Если дискриминант больше нуля, то уравнение имеет два корня.
Если дискриминант равен нулю, то уравнение имеет один корень.
Если дискриминант меньше нуля, то уравнение не имеет корней.

Несмотря на то, что есть несколько формул дискриминанта, чаще всего используют первую:

так как она относится к формуле:

которая является универсальной формулой нахождения корней квадратного уравнения. Данная формула подходит даже для неполных квадратных уравнений.

Видео:Как решать квадратные уравнения без дискриминантаСкачать

Решение квадратных уравнений через дискриминант

Для решения квадратного уравнения по формуле можно сначала вычислить дискриминант и сравнить его с нулём. В зависимости от результата, либо искать корни по формуле, либо сделать вывод, что корней нет.

Пример 1. Решить уравнение:

Определим, чему равны коэффициенты:

D = b 2 — 4ac = (-4) 2 — 4 · 3 · 2 = 16 — 24 = -8,

Определим, чему равны коэффициенты:

D = b 2 — 4ac = (-6) 2 — 4 · 1 · 9 = 36 — 36 = 0,

Уравнение имеет всего один корень: