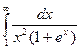Запрошуємо усіх хто любить цікаві задачі та головоломки відвідати групу! Зараз діє акція — підтримай студента! Знижки на роботи + безкоштовні консультації.
Контакты
 |
|
|
|
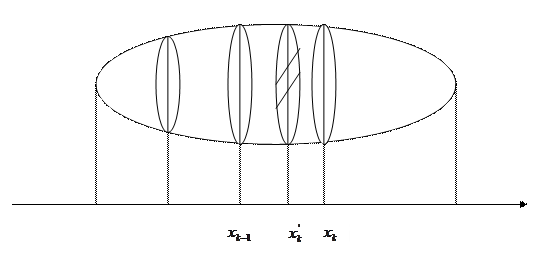
Пусть ОХ некоторое выбранное направление и S(x) – площадь поперечного сечения плоскостью перпендикулярной оси ОХ в точке с абсциссой х. Функцию S(x) будем предполагать известной и непрерывно меняющейся при изменении х. Проектируя тело на ось ОХ, получим некоторый отрезок [a,b], дающий линейные размеры тела в направлении оси ОХ.
Разобьем данное тело на элементарные слои плоскостями, перпендикулярными оси ОХ. Точки пересечения этих плоскостей с осью ОХ соответственно 





Объемом тела называют предел объема указанного ступенчатого тела, приближенно заменяющего данное тело, при 

По определению 


Пример
Найти объем пирамиды с основанием В и высотой Н
Решение
Ось ОХ перпендикулярна поверхности В и направлена из точки О. S – площадь сечения пирамиды плоскостью, находящейся на расстоянии х от вершины. Так как площади поперечных сечений пирамиды относятся как квадраты расстояний их от вершины, то имеем

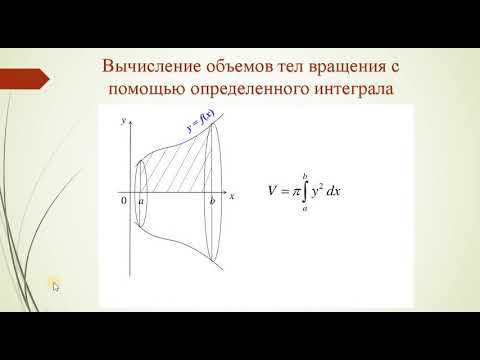
Объем тела вращения
Задача
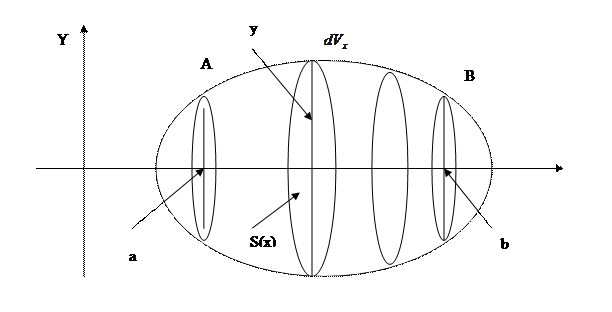
Найти объем тела, образованного вращением вокруг оси ОХ криволинейной трапеции aABb, ограниченной данной непрерывной линией 

|
Эта задача – частный случай задачи, рассмотренной выше. Здесь площадь переменного поперечного сечения S=S(x), соответствующего абсциссе х, есть круг радиуса у, поэтому 

Задача
Найти объем тела, образованного вращением вокруг оси ОУ криволинейной трапеции cCDd, ограниченной данной непрерывной линией 

По аналогии с формулой (2) 

Примеры
- Вычислить объем тела, полученного вращением вокруг оси ОХ криволинейной трапеции, ограниченной линиями
Пределы интегрирования a=1,b=6, функция
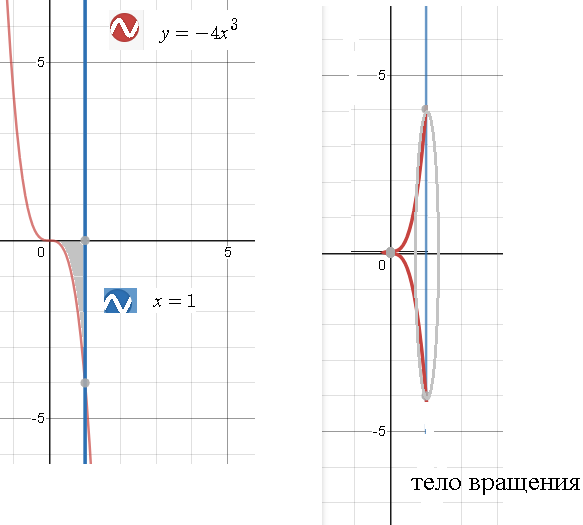
- Вычислить объем тела, полученного в результате вращения вокруг оси ОХ криволинейной трапеции, ограниченной линией
, осями координат и прямой х=1
Пределы интегрирования a=0,b=1, функция
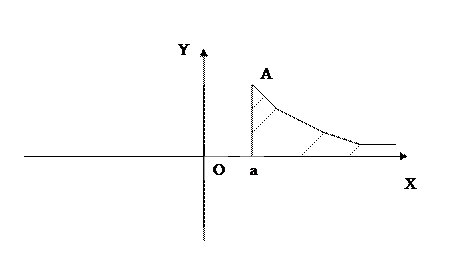
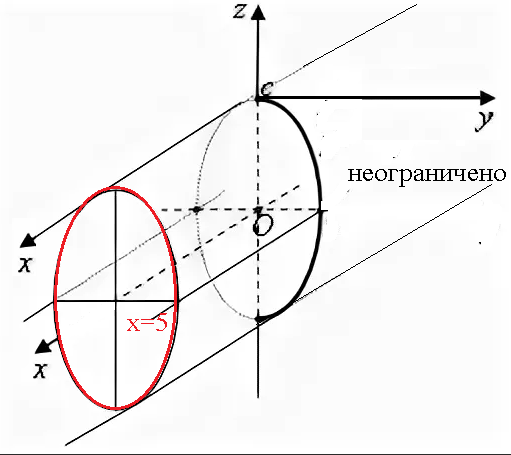
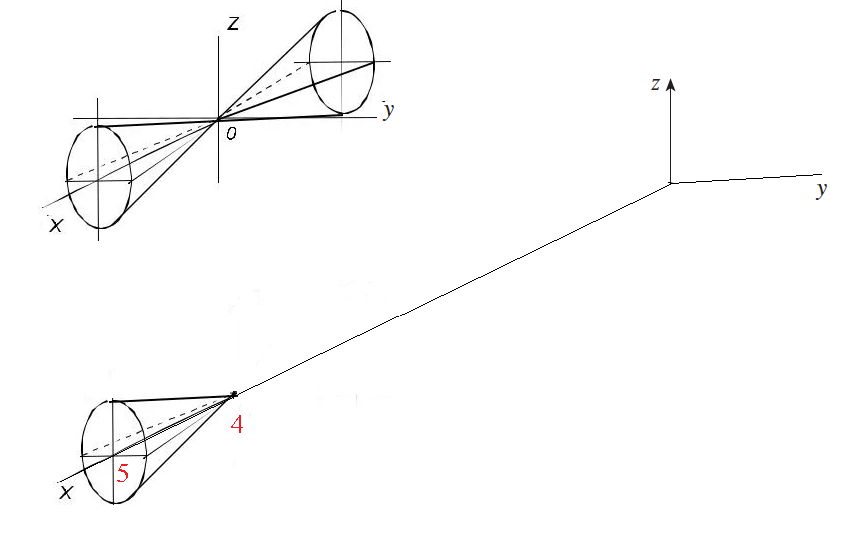
- Определить объем тела, ограниченного поверхностью, полученной от вращения эллипса
вокруг оси ОХ (и ОУ)
Так ка эллипс симметричен относительно осей координат, то достаточно найти объем, образованный вращением вокруг оси ОХ площади ОАВ, равной ¼ площади эллипса, и полученный результат удвоить.
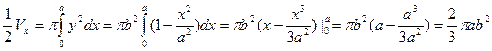

Несобственные интегралы
При определении интеграла 
1) Отрезок интегрирования [a,b] – конечен;
2) f(x) определена и непрерывна на отрезке [a,b].
Такой определенный интеграл называется собственным (название опускается).
Если нарушается по крайней мере одно из двух условий 1) или 2), то (1) называется несобственным определенным интегралом.
Рассмотрим смысл этого понятия для двух простейших случаев
I. Пусть f(x) непрерывна при 

Если предел (2) существует, то несобственный интеграл с бесконечным пределом интегрирования, стоящий в левой части равенства (2), называется сходящимся и его значение определяется формулой (2); в противном случае равенство (2) теряет смысл, несобственный интеграл, стоящий слева, называется расходящимся и ему не приписывается никакого числового значения.
Геометрически для неотрицательной на 
Пусть F(x) первообразная для f(x). На основании формулы (2) имеем



1)
2) Установить, при каких значениях 
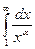
Решение Так как при 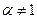
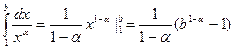

Если 

Если 

Если 

3.Вычислить 

Вычислим 
Во многих случаях бывает достаточно установить, сходится данный интеграл или расходится, оценить его значение. Для этого могут быть полезны следующие теоремы.
Теорема 1
Если для любого х 




- Исследовать, сходится ли интеграл
При 
Теорема 2
Если для любого х 



- Исследовать, сходится ли интеграл
При 
Для функции меняющий знак в бесконечном интервале, имеет место следующая теорема
Теорема 3
Если интеграл 

- Исследовать, сходится ли интеграл
При 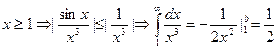
📺 Видео
Вычисление площадей и объемов с помощью определённого интегралаСкачать

Вычисление объемов тел вращения (применение определенного интеграла)Скачать
Объем тела вращенияСкачать

Объем через тройной интеграл в сферической системе координатСкачать

Объем тела вращения на примере тора. 2 способаСкачать

Урок 28 (осн). Вычисление массы и объема тела по плотностиСкачать

Интегралы №13 Объем тела вращенияСкачать

Объем через тройной интегралСкачать

Объем через двойной интегралСкачать
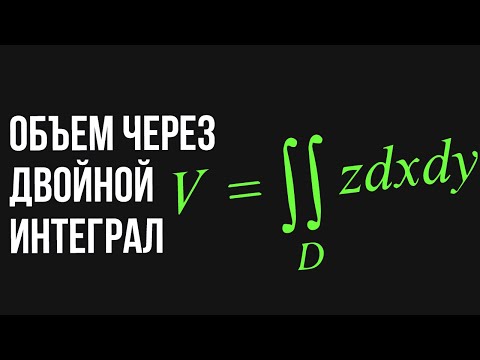
Видеоурок "Объем тела вращения"Скачать

Метод сеченийСкачать

Объем параболоида: тройной интеграл в цилиндрической системе координатСкачать

Применение определенного интеграла при решении геометр. и физических задач. Практ. часть. 11 класс.Скачать

Как строить сеченияСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Математический анализ, 44 урок, Тройной интегралСкачать

Расчёт массы и объёма тела по его плотности | Физика 7 класс #16 | ИнфоурокСкачать










 , осями координат и прямой х=1
, осями координат и прямой х=1

 вокруг оси ОХ (и ОУ)
вокруг оси ОХ (и ОУ)