Условие
Помогите пжл с решением двух задач по математике под цифрой 2
Задача 1. Вычислить объём тела, заданного представленными уравнениями, используя его поперечные сечения
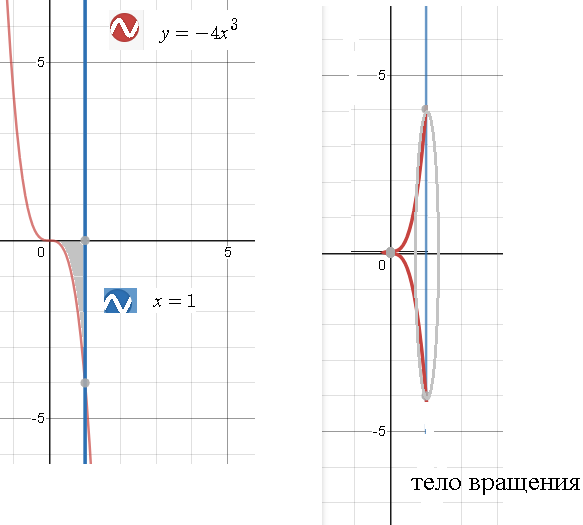
Задача 2. Вычислить объём тела, образованного вращением вокруг оси Ох фигуры, заданной представленными линиями 
Решение
Возводим в квадрат:
[m](z+4)^2+y^2=32[/m] — это уравнение эллипса в пл уOz, а значит цилиндрической поверхности в пространстве
Это бесконечная поверхность, вдоль оси Ох. См. рис.
По условию ограничена пл. х=5 Получается с одной стороны.
А значит тело неограниченное.
Поэтому я думаю, что в условии [b]опечатка.[/b]
[b]Наверное[/b] ( что не почетно, гадать, что должно быть )
так:
Возводим в квадрат и получаем:
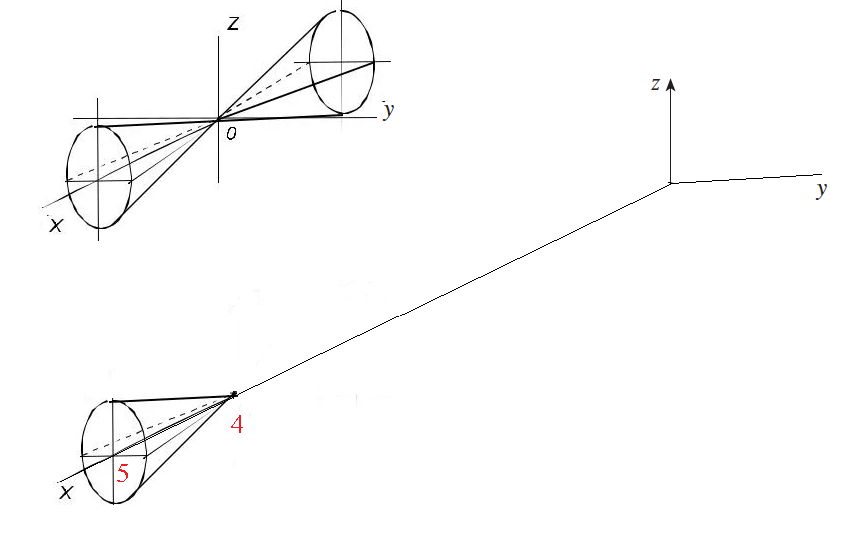
[m](x-4)^2=y^2+2z^2[/m] — это коническая поверхность.
Эллиптический конус в с вершиной в точке (4;0;0) cм скрин 3.
Но уравнение в условии задачи [m]x=4+ sqrt[/m] означает, что дана только та часть, которая выше точки (4;0;0) по направлению оси Ох.
И тогда все замечательно, потому как есть ограниченный слой на участке от 4 до 5
Рассекаем этой слой плоскостью x=h
4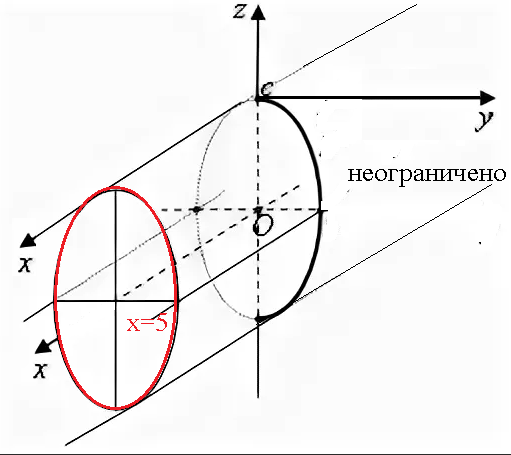 
Видео:Вычисление площадей и объемов с помощью определённого интегралаСкачать
Объем тела вращения онлайн
Рассмотрим некоторую функцию , непрерывную на отрезке :
Если мы будем вращать данную функцию вокруг оси , то образуется некоторое тело вращения:
Объём полученной фигуры можно посчитать, вычислив вот такой интеграл:
Теперь рассмотрим некоторую функцию , непрерывную на отрезке :
На этот раз будем вращать данную функцию вокруг оси . В результате получим следующее тело вращения:
Его объём вычисляется по формуле:
Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha позволяет вычислить объём тела вращения, заданного практически любой функцией. Для этого, в калькулятор нужно ввести саму функцию, границы в пределах которых будет вычисляться объём тела и выбрать ось вращения.
Видео:Объем через тройной интегралСкачать
Вычислить объем тела заданного представленными уравнениями используя его поперечные сечения онлайн
Запрошуємо усіх хто любить цікаві задачі та головоломки відвідати групу! Зараз діє акція — підтримай студента! Знижки на роботи + безкоштовні консультації.
Контакты
 |
