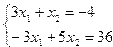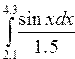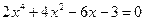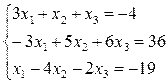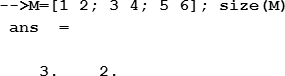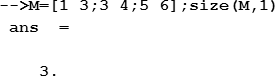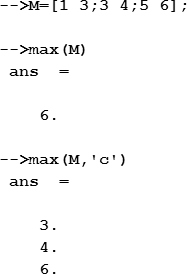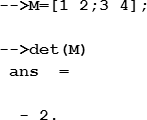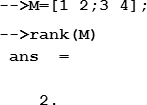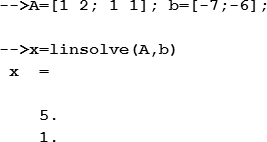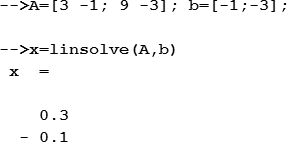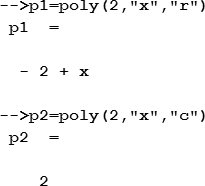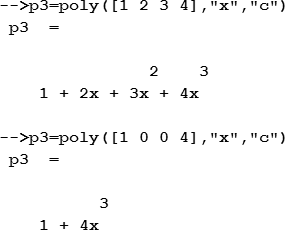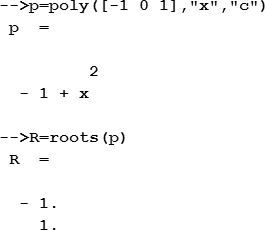Краткие теоретические сведения
В Scilab вычисление определенного интеграла методом трапеций реализовано функцией
где x –вектор значений аргумента подынтегральной функции на отрезке интегрирования, y –вектор значений, полученных при вычислении подынтегральной функции для элементов вектора x.
Например, для вычисления 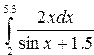
| Фрагмент программы x=2:0.01:5.3 y =2*x./(sin(x)+1.5) integral = inttrap(x,y)disp(integral) | Результат 30.436962 |
Для вычисления определенного интеграла с использованием алгоритма квадратурных формул предназначена функция
Integrate(fun, x, a, b, ,er1 ,er2),
где fun– подынтегральная функция в символьном виде, x – переменная интегрирования в символьном виде, a, b –пределы интегрирования, er1,er2 –абсолютная и относительная погрешности интегрирования (необязательные параметры).
Например, для вычисления 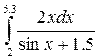
| Фрагмент программы z=integrate(‘2*x./(sin(x)+1.5)’, ‘x’, 2, 5.3)disp(z) | Результат 30.437056 |
Универсальная команда интегрирования:
[integral,err]=intg(a, b, name ,er1,er2),
где a, b –пределы интегрирования, name – имя подынтегральной функции (может быть задана с помощью внешней функции), er1,er2 –абсолютная и относительная погрешности интегрирования (необязательные параметры). Функция intgвозвращает значение интеграла (integral) и погрешность вычислений (err).
Внешнюю функцию можно задать командой
deff(‘переменная=имя функции(параметр)’, ‘символьное представление функции’) Например, deff(‘y=F(x)’, ‘y=2*x./(sin(x)+1.5)’).или
function переменная = имя функции(параметр-аргумент функции)
операторы, вычисляющие значение функции
endfunctionНапример, function y=f(t) y=t^2/sqrt(3+sin(t)) endfunctionилиfunction y=f(t),y=t^2/sqrt(3+sin(t)),endfunction
Ниже приводится пример вычисления интеграла 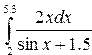
| Фрагмент программы function y=f(x) y=2*x./(sin(x)+1.5)endfunctionz=intg(2,5.3,f), disp(z) | Результат 30.437056 |
Для решения нелинейных уравнений в Scilab используется функция
где x0 –начальное приближение корня, f– функция, описывающая левую часть уравнения f(x)=0.
Например, для решения уравнения 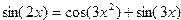
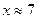
| Фрагмент программы deff(‘y=F(x)’, ‘y=sin(2*x)-cos(3*x.^2)-sin(3*x)’)root=fsolve(7,F)disp(root) | Результат 6.9755674 |
Для решения полиномиальных уравнений вида 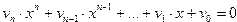
где а – вектор коэффициентов перед неизвестными полинома размерностью n+1(n – порядок полинома).
Результатом работы этой функции будет вектор корней полинома размерностью n.
Пример решения полиномиального уравнения 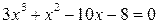
| Фрагмент программы v=[3 1 -10 -8]R=roots(v)disp(R) | Результат 2. -1.3333333 — 1. |
Для уравнения 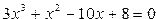
| Фрагмент программы v=[3 1 -10 8]R=roots(v)disp(R) | Результат — 2.2935835 0.9801251 + 0.4494650i 0.9801251 — 0.4494650i |
Функция rootsможет также принимать в качестве параметра полином, созданный функциейpolyи представляющий собой левую часть уравнения 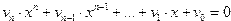
где a –вектор коэффициентов полинома записанных в обратном порядке, x — символьная переменная, f1– символьная переменная, принимающая значения ‘c’ или ‘r’ (roots или coeff).
Например, чтобы создать полином 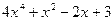
| Фрагмент программы p=poly([3 -2 1 0 4],’x’,’c’)disp(p) | Результат 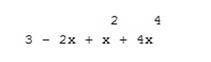 |
Для решения уравнения 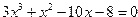
| Фрагмент программы p=poly([-8 -10 1 3],’x’,’c’)R=roots(p)disp(R) | Результат 2. — 1.3333333 — 1. |
Для решения систем линейных уравнений в Scilab есть следующие способы:
— применение операции левого матричного деления;
— использование обратной матрицы.
Если задана система линейных алгебраических уравнений вида:
где А – матрица коэффициентов перед неизвестными системы, В – вектор свободных членов, то решение системы может быть найдено в виде:
То же самое решение может быть получено с помощью обратной матрицы, например:
Например, решить систему уравнений
| Фрагмент программы A=[3 1;-3 5]; B=[-4 ;36]; X=inv(A)*B, disp(X)илиX1=AB , disp(X1) | Результат — 3.1111111 5.3333333 |
Для решения систем нелинейных уравнений можно использовать функцию
где x0 –вектор начальных приближений для неизвестных, f –функция, определяющая систему
Например, решение системы 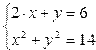
| Фрагмент программы function [y]=fun(x) y(1)=2*x(1)+x(2)-6 y(2)=x(1)^2+x(2)^2-14endfunctionX0=[1;1]R=fsolve(X0,fun)disp(R) | Результат 1.2338096 3.5323808 |
Задание 1. Вычисление определенного интеграла
Постановка задачи. Вычислить числовое значение интеграла от этой функции в заданных пределах интегрирования методом трапеций, методом квадратурных формул и с помощью функции intg.
Шаг 1. Создадим вектор X, значения которого будут изменяться от 2,1 до 4,3 с шагом 0.01.
Шаг 2. Создадим вектор Y, каждое значение которого вычисляется по формуле 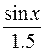
Шаг 3. Применим команду inttrap(X, Y).
Шаг 4. Используем функцию integrate,задав подынтегральную функцию в символьном виде.
Шаг 5. Определим внешнюю функцию с помощью команды deffили конструкции function
Шаг 6. Выведем результаты, используя команду disp.
| Программа | Результат выполнения |
| X =2.1:0.01:4.3 Y =sin(X)/1.5 integral_1 = inttrap(X,Y)integral_2=integrate(‘sin(x)/1.5’, ‘x’, 2.1, 4.3)disp(integral_1)disp(integral_2) | — 0.0693640 — 0.0693646 |
| deff(‘y=F(x)’,’y=sin(x)/1.5′); integral_3=intg(2.1,4.3,F)function y=f(x) y=sin(x)/1.5endfunctionintegral_4=intg(2.1,4.3,f)disp(integral_3)disp(integral_4) | — 0.0693646 — 0.0693646 |
Индивидуальные задания приведены в таблице 3.4.
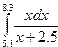 | 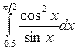 | 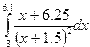 |
 | 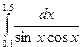 | 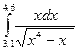 |
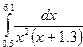 | 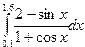 | 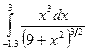 |
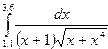 | 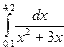 | 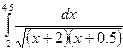 |
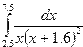 | 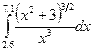 | 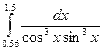 |
Задание 2. Поиск корней уравнения, графическая интерпретация
Постановка задачи. Найти корень уравнения для заданного начального приближения. Выполнить графическую интерпретацию результата.
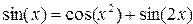 |  |
Шаг 1. Определим внешнюю функцию с помощью команды deffили конструкции function
Шаг 2. Найдем корень уравнения с помощью функции fsolve,подставив в качестве первого параметра заданное начальное приближение.
Шаг 3. Выведем результат, используя команду disp.
Шаг 4. Выполним графическую интерпретацию результата. Для этого зададим аргумент функции из левой части уравнения таким образом, чтобы найденный корень попадал в диапазон между первым и последним элементом вектора. Построим график функции из левой части уравнения с помощью plot.Построим также линию y=0 и отметим точку с абсциссой, равной корню, и ординатой, равной значению функции для корня.
| Программа | Результат выполнения |
| deff(‘y=F(x)’, …’y=sin(x)-cos(x.^2)-sin(2*x)’)root=fsolve(1,F)disp(root)x=0.5:0.01:2.5plot(x,F(x),’-b’,root,F(root),’xr’,x,0,’-k’) | 1.1695683 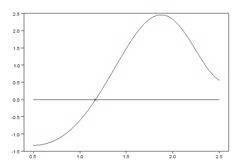 |
Индивидуальные задания приведены в таблице 3.5
| Вариант | Уравнение | Начальноеприближение |
| 1. | 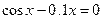 | 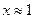 |
| 2. | 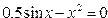 | 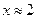 |
| 3. | 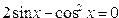 | 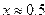 |
| 4. | 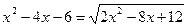 | 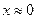 |
| 5. | 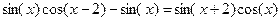 | 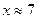 |
| 6. | 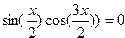 |  |
| 7. | 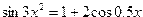 | 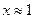 |
| 8. | 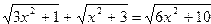 | 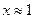 |
| 9. | 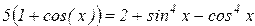 | 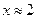 |
| 10. | 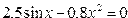 | 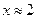 |
| 11. | 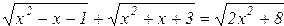 | 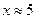 |
| 12. | 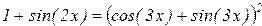 | 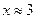 |
| 13. | 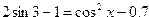 | 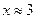 |
| 14. |  | 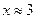 |
| 15. | 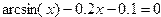 | 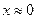 |
Задание 3. Поиск корней полиномиального уравнения, графическая интерпретация
Постановка задачи. Найти все корни полиномиального уравнения. Выполнить графическую интерпретацию для одного из найденных действительных корней.
Шаг 1. Создадим вектор коэффициентов полинома в левой части уравнения (или полином с помощью poly)
Шаг 2. Найдем корни уравнения с помощью функции roots.
Шаг 3. Выведем результат, используя команду disp.
Шаг 4. Выполним графическую интерпретацию результата. Для этого зададим аргумент функции из левой части уравнения таким образом, чтобы выбранный действительный корень попадал в диапазон между первым и последним элементом вектора. Построим график функции из левой части уравнения с помощью plot.Построим также линию y=0 и отметим точку с абсциссой, равной корню, и ординатой, равной значению функции для корня.
| Программа | Результат выполнения |
| v=[2 0 4 -6 -3]R=roots(v)disp(R)root=R(3)x=0.5:0.01:2y=2*x.^4+4*x.^2-6*x-3F_root=2*root^4+4*root^2-6*root-3plot(x,y,’-b’,root,F_root,’xr’,x,0,’-k’) | — 0.4129576 + 1.7282075i — 0.4129576 — 1.7282075i 1.2164706 — 0.3905555 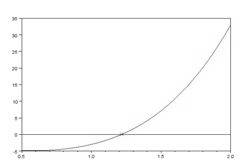 |
Индивидуальные задания приведены в таблице 3.6.
| Вариант | Уравнение |
| 1. | 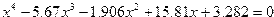 |
| 2. |  |
| 3. | 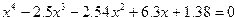 |
| 4. | 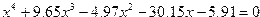 |
| 5. | 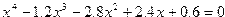 |
| 6. | 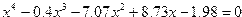 |
| 7. | 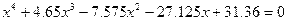 |
| 8. | 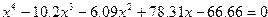 |
| 9. | 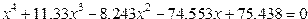 |
| 10. | 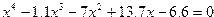 |
| 11. | 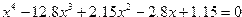 |
| 12. | 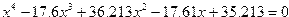 |
| 13. | 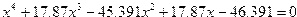 |
| 14. |  |
| 15. | 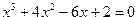 |
Задание 4. Решение системы линейных уравнений
Постановка задачи. Решить систему линейных уравнений.
Шаг 1. Создадим матрицу коэффициентов при неизвестных
Шаг 2. Создадим вектор свободных членов.
Шаг 3. Умножим матрицу, обратную к матрице коэффициентов, на вектор свободных членов (или применим операцию левого матричного деления).
Шаг 4. Выведем результат, используя команду disp.
| Программа | Результат выполнения |
| A=[3 1 1;-3 5 6;1 -4 -2]; B=[-4 ;36;-19]; X=inv(A)*B disp(X) | — 3. 3. 2. |
Индивидуальные задания приведены в таблице 3.7.
| № | Система уравнений | № | Система уравнений |
| 1. | 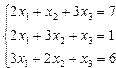 | 2. | 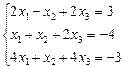 |
| 3. | 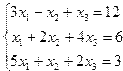 | 4. | 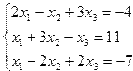 |
| 5. | 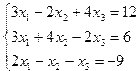 | 6. | 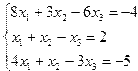 |
| 7. | 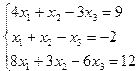 | 8. | 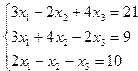 |
| 9. | 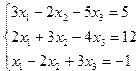 | 10. | 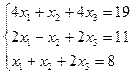 |
| 11. | 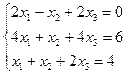 | 12. | 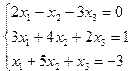 |
| 13. | 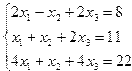 | 14. | 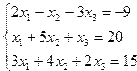 |
| 15. | 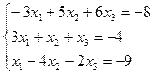 | 16. | 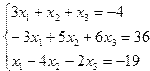 |
- Статьи к прочтению:
- Метод Крамера за 3 минуты. Решение системы линейных уравнений — bezbotvy
- Похожие статьи:
- Основы работы с системой технических расчетов Scilab
- Учебное пособие Москва 2008 Тропин И. С., Михайлова О. И., Михайлов А. В. Т 742
- Главная > Документ
- Решение систем линейных уравнений
- Построение графиков
- Функция plot
- Изображение сетки в графической области
- Вывод названий графика и осей
- Нанесение описания линий
- Примеры вычислений в Scilab
- Вычисление площади круга и длины окружности
- Вычисление длины вектора
- Построение касательной к кривой в заданной точке
- Решение уравнения графическим способом
- Решение биквадратного уравнения
- Вывод значения выражения на экран
- Вычисление определенного интеграла
- Задания для самоконтроля
- Глоссарий
- Список литературы
- Приложение А
- 📹 Видео
Статьи к прочтению:
Метод Крамера за 3 минуты. Решение системы линейных уравнений — bezbotvy
Похожие статьи:
Приближенное вычисление интегралов Приближённое вычисление определённого интеграла основано на геометрическом смысле интеграла и сводится к приближённому…
Задание: графически и численно решить систему нелинейных алгебраических уравнений, на примере поиска точек пересечения двух функций. Исходные данные:…
Видео:Решение уравнений в ScilabСкачать

Основы работы с системой технических расчетов Scilab
Решение задач линейной алгебры
Функции для нахождения числовых характеристик матриц
Для определения количества строк и столбцов матрицы М используют функцию size, аргументом которой является имя массива:
Если нужно определить количество только строк или только столбцов, то синтаксис функции модифицируется: добавляется второй аргумент, который имеет значение «1» или «r», если следует определить количество строк, «2» или «с» — если столбцов. Например:
Общее количество элементов матрицы или длину вектора вычисляет функция length, аргументом которой является имя матрицы или вектора:
Для определения максимального значения элемента матрицы или вектора используется функция max, аргументом которой является имя матрицы или вектора. Если нужно определить максимальное значение для каждого из строк или столбцов матрицы, то синтаксис функции модифицируется: добавляется второй аргумент, который имеет значение «r», если следует определить максимальное значение для каждой строки, или «c» — если для каждого столбца:
Аналогично используется функция min, предназначенная для определения минимального значения элемента матрицы или вектора.
Для вычисления определителя (детерминанта) квадратной матрицы используется функция det, аргументом которой является имя матрицы:
Для вычисления ранга матрицы используется функция rank, аргументом которой является имя матрицы:
Функции, реализующие численные алгоритмы решения задач линейной алгебры
Вычисление матрицы, обратной М
Напомним, что обратной по отношению к матрице М называется такая матрица, которая при ее умножении на матрицу М дает единичную матрицу.
Как видим, обратная матрица А достаточно близка к единичной, но все же полностью ею не является, что является следствием погрешности численных вычислений.
Scilab позволяет решать системы линейных алгебраических уравнений вида Ax=b. В документе для значений A формируется матрица коэффициентов при неизвестных, каждая строка которой содержит коэффициенты одного уравнения, а для значений b формируется вектор-столбец из свободных коэффициентов.
После этого для решения системы используется функция linsolve, имеющая такой синтаксис:
где A — это матрица коэффициентов при неизвестных, b — вектор-столбец свободных коэффициентов.
Функция возвращает найденные значения неизвестных системы в виде вектора.
Таким образом, решение системы линейных уравнений 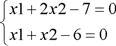
Искомые значения: х1=5, х2=1.
Если система не имеет решения, то об этом выдается сообщение «WARNING: Conflicting linear constraints!» (Конфликтующие условия для линейных уравнений). Например, такая ситуация возникнет при попытке решения системы линейных уравнений 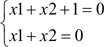
Система линейных алгебраических уравнений может иметь множество решений. В таком случае функция возвращает только одно. Ниже приведен пример такой ситуации при решении системы линейных уравнений 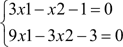
Работа с полиномами
Напомним, что полиномом или алгебраическим уравнением называется уравнение вида a0x n + a1x n-1 + . + an-1x + an.
Для создания полинома используется функция poly.
где р — это имя полинома (его можно и не задавать).
Аргументы функции: a — матрица или вещественное число, x — символьная переменная, «flag» — символьная переменная, которая определяет способ задания полинома и имеет значение «roots» (допускается сокращение «r») или «coeff» («c»). По умолчанию — «roots». Если «roots» имеет значение «r», то полином создается с параметрами ai для соответствующих символьных переменных xi. Если «flag» имеет значение «c», то значения параметров ai воспринимаются как корни, для которых нужно рассчитать коэффициенты полинома.
Следующий пример демонстрирует использование функции poly для создания полиномов р1, который имеет корень «2» и р2 с коэффициентом «2»:
В следующих примерах создаются полиномы с соответствующими коэффициентами для кубического уравнения.
С полиномами можно производить действия умножения, создавать из них дроби (деление), складывать и вычитать.
Решение уравнения с одним неизвестным
Scilab может решать алгебраическое уравнение с одним неизвестным. Например, нужно найти корни уравнения x 2 = 1. Если — как в данном примере — уравнение не имеет вида полинома, то его следует предварительно преобразовать в полином: x 2 — 1 = 0. После этого используется функция roots, единственным аргументом которой является имя полинома. Функция возвращает найденные корни полинома.
Если уравнение не имеет решения на множестве вещественных чисел (x 2 + 1 = 0), то Scilab ищет решение среди комплексных чисел:
Вычисление сумм элементов матрицы
Для вычисления суммы значений элементов матрицы используется функция sum.
Если следует вычислить отдельно сумму значений для каждого столбца, то вторым аргументом функции является число «1» или буква «с», а если для строки, то — «2» или буква «r».
Вычисление произведения элементов матрицы
Для вычисления произведения используется функция prod.
Если следует вычислить отдельно произведение значений каждого столбца, то вторым аргументом функции является число «1» или буква «с», а если для строки, то — «2» или буква «r».
Дифференциалы
Для нахождения дифференциалов в определенной точке используется функция numdiff, первый аргумент которой является именем функции, которую нужно продифференцировать, а второй — координата точки, в которой нужно вычислить производную.
Видео:Решение биквадратных уравнений. 8 класс.Скачать

Учебное пособие Москва 2008 Тропин И. С., Михайлова О. И., Михайлов А. В. Т 742
Главная > Документ
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
Видео:Решение трансцендентных уравнений в Scilab.aviСкачать

Решение систем линейных уравнений
Рассмотрим решение системы из трех уравнений с тремя неизвестными переменными 
Прежде чем приступить к формированию задачи для Scilab, необходимо привести систему уравнений к виду
Для нашего примера система будет выглядеть следующим образом:
Для решения подобных систем уравнений в Scilab существует функция linsolve . Обращение к ней выглядит следующим образом:
K — таблица, составленная из коэффициентов уравнений системы (см. пп 7.1.2), причем она сформирована таким образом, что каждая строка представляет собой список коэффициентов одного из уравнений системы, а каждый столбец — список коэффициентов при одноименных переменных, то есть если первым элементом в первой строке является коэффициент при y , то первыми элементами других строк также должны быть коэффициенты при y в соответствующих уравнениях.
K= 
Для решаемой системы:
K= 
k — столбец, содержащий свободные (стоящие после знака «=») коэффициенты.
Примечание: при задании в Scilab k должен быть именно столбцом , поэтому перечисление переменных нужно делать через «;» (см. пп. 7.1.1).
k= 
Для решаемой системы

После того как элементы списков K и k определены, приступим к решению системы в Scilab (Листинг 42).
Зададим таблицу коэффициентов при неизвестных переменных.
Зададим столбец независимых коэффициентов.
Решим уравнение при помощи функции linsolve (результат решения в данном случае присваивается переменной «reshenie»).
Результатом решения станет список значений переменных 
Задания для самоконтроля:
Решить системы уравнений:
Видео:Scilab Лабараторная 1.1Скачать

Построение графиков
Scilab содержит набор функций для графического представления информации. Для построения графиков функции одной переменной, например, служат функции plot и polarplot . Первая — позволяет строить графики в декартовых координатах, вторая — изображает графики в полярных координатах. Обе эти функции требуют предварительного определения списка значений аргумента и списка соответствующих значений функции, график которой необходимо построит. Списки аргументов и значений функции указываются первым и вторым аргументами при вызове plot и polarplot . Ниже подробнее будет рассмотрено использование функции plot . Она же может использоваться для построения графиков в полярных координатах, используя очевидную связь между декартовыми и полярными координатами.
Функция plot
Функция plot предназначена для построения двумерных графиков функции одной переменной вида f=f ( x ) .
Обращение к функции plot выглядит следующим образом:
где x — список значений независимой переменной, а y — список значений функции f в этих точках. Соответственно для того, чтобы построить график в Scilab, необходимо создать список значений переменной и список значений функции в этих точках.
График, построенный при помощи функции plot , представляет собой ломаную линию, соединяющую значения функции, вычисленные в заданных точках. Следовательно, чтобы получить гладкий график, необходимо вычислить значение функции в большом количестве точек.
Рассмотрим пример построения графика функции sin 2 (2 x ) (Листинг 43).
Список x получает значения от 

Список y содержит значения функции для каждого элемента в x.
В результате обращения к функции plot открылось окно графического редактора Scilab, содержащее график функции (рис. 3).
Рис. 3. Графическое окно Scilab
Из-за того, что значение функции было вычислено в большом количестве точек, т.е. был выбран малый шаг разбиения промежутка построения, равный 0.01, график функции получился гладким без видимых изломов.
При последующем обращении к функции plot в текущем сеансе график будет построен в том же окне и линия будет того же цвета, что и у предыдущего графика. Для построения нескольких графиков в одной области удобнее использовать обращение к функции plot следующего вида: plot(x1,y1,x2,y2,x3,y3) , где x 1— список значений переменной x, в которых должно быть вычислено значение функции f 1= y 1( x ), x2 — список значений переменной x, в которых должно быть вычислено значение функции f 2= y 2( x ), и т.д. Если построение происходит в одной области, в качестве х1, х2, х3 может выступать один и тот же список.
Построим в одной области графики функций: f 1=sin( x ); f 2=cos( x ); f 3=
В данном случае список х является списком аргументов для всех трех функций.
Результат работы функции plot , обращение к которой содержит Листинг 44, можно видеть на рис. 4.
Рис. 4. Графическое окно Scilab
Как видно, графики функций в данном случае автоматически изображаются разными цветами.
Вид графика можно изменять, добавив при обращении к функции plot помимо основных аргументов еще один аргумент — строку, состоящую из трех символов, которые будут определять цвет линии, тип маркера и тип линии графика. Обращение к функции plot будет выглядеть: plot(x,y,string) , в случае, если необходимо построить один график, или plot(x1,y1,string1,x2,y2,string2,x3,y3,string3. xn,yn,stringn) — для n графиков.
Строка string выглядит следующим образом
Символы пишутся один за другим без разделителей.
Параметр1 определяет цвет линии графика:
Значения параметра функции plot, определяющего цвет графика
Параметр2 определяет тип маркера графика:
Значение параметра, определяющего тип маркеров (точек) графика
треугольник вершиной вниз
треугольник вершиной вверх
треугольник вершиной вправо
Параметр 3 определяет тип линии графика:
Значения параметра, определяющего тип линии графика
Если один из символов не указан, его значение выбирается по умолчанию, при неуказанном типе маркера — маркер будет отсутствовать.
Построим 3 графика на отрезке 
f 1 (x)=x 2 — пунктирная линия желтого цвета;
f 2 (x)= 1 +x —штриховая линия голубого цвета;
f 3 (x)=e x —сплошная линия черного цвета.
Решение (Листинг 45):
Зададим список точек c именем x , в которых будут вычислены значения функций.
Вычислим значения функции f 1 в точках списка x.
Вычислим значения функции f 2 в точках списка x .
Вычислим значения функции f 3 в точках списка x .
Построим по вычисленным значениям графики функций с заданными параметрами (см. табл. 11.1 и 11.3).
В результате выполнения команд, приведенных в Листинге 45, в графическом окне Scilab будут построены графики функций f 3( x ) , f 2( x ) , f 1( x ) (рис. 5).

Изображение сетки в графической области
Для изображения сетки следует воспользоваться функцией xgrid(color) . Color — аргумент функции, он определяет цвет линий сетки. Общий вид аргумента: a 1 a 2 a 3 , где каждый из параметров а 1 , а 2 и а 3 может принимать два значения — 0 или 1. Параметр а 1 определяет наличие (при а 1 = 1) или отсутствие (при а 1 =0) красной составляющей в цвете линии, а 2 — зеленой и а 3 — синей. Различные комбинации значений этих параметров позволяют получать различные цвета. Например, в результате вызова функции xgrid(100) в графической области будет отображена сетка красного цвета. Значения параметров следует вводить подряд без разделителей.
Вывод названий графика и осей
Вывод названий осуществляется с помощью функции
xtitle(name, xname, yname),
здесь name — название графика, x name — название оси Х , y name — название оси Y .
Нанесение описания линий
Нанесение осуществляется вызовом функции legend. Обращение к этой функции выглядит следующим образом:
line1 — описание (название) первого графика, line2 — второго . line n – имя n -го графика;
place определяет месторасположение описания: если place=1, то описание будет расположено в верхнем правом углу графической области (если значение place не указано, то по умолчанию place=1), 2 — в верхнем левом углу, 3 — в нижнем левом углу, 4 — в нижнем правом углу, 5 — положение определяется пользователем после изображения графика;
frame – может принимать два значения %t и %f (по умолчанию frame =%t ), если frame =%t , то описание будет заключено в рамку, если же frame =%f — рамка отсутствует.
Задания для самоконтроля:
Построить в одном графическом окне графики функций 



Построить графики sin( x ) и cos( x ) на промежутке от 

Построить три графика произвольных функций одного цвета в одном графическом окне.
Видео:Алгоритмы. Нахождение корней уравнений методом деления отрезка пополам.Скачать

Примеры вычислений в Scilab
Вычисление площади круга и длины окружности
Вычислить площадь круга и длину окружности радиуса r =5.78.
Площадь круга и длина окружности вычисляются по формулам: 

Вычисление длины вектора
Пусть 



Построение касательной к кривой в заданной точке
Построить график функции f ( x )=5— х 2 и касательной к графику функции в точке х =2.
Касательная прямая определяется уравнением l ( x ) =kx+b , где k=f ‘ ( x 0 ) , b=f(x 0 )—k*x 0 , x 0 =a — координата точки касания.
Решение задачи в Scilab (Листинги 48 — 52):
Зададим функцию 
—>function d=f(x), d=5-x^2 endfunction
Определим функцию f ( x ) = 5— х 2 .
Определим x 0 — координату точки касания.
Для того, чтобы построить касательную прямую необходимо сначала определить коэффициенты b и k в уравнении прямой (Листинг 49).
Определим коэффициент k . Для этого с помощью функции numdiff (см гл. 6) найдем производную функции в точке x 0=2.
Определим коэффициент b по формуле: 
Определим функцию 


—>function g=kas(x), g=k*x+b endfunction
Определим xgraph — список точек для построения графика (см. пп. 7.1.1) (Листинг 51).
Определим список, содержащий значения x на интервале от —5 до 5 с шагом 0,01.
Вычислим значения функций f ( x ) и kas ( x ) в точках из списка xgraph (см п 7.2) (Листинг 52).
Аргументом функций f ( x ) и kas ( x ) является список xgraph, это значит что значение функции будет вычислено во всех точках списка. Результатом вызова функции kas(xgraph) будет список значений функции в точках списка xgraph.
Используя функцию plot (см. п. 11.1), построим графики функций f ( x ) и kas ( x ) (Листинг 53).
Рис. 6. Результат вызова функции plot
Используя списки xgraph, fgraph, kasgraph, изобразим графики функций f ( x ) и kas ( x ) (рис. 6).
Решение уравнения графическим способом
Пусть необходимо решить уравнение 
Преобразуем исходное уравнение к виду 

Чтобы найти корни уравнения, необходимо найти точку пересечения графиков функций 


Графики пересекаются при 
Решение биквадратного уравнения
Найти корни уравнения 
Приведем уравнение к виду 

Поиск нулей полинома при помощи Scilab (см. гл. 9, выражение (11) приведен в Листинге 55.
Вывод значения выражения на экран
Вывести на экран значение числа 
Для вывода числа на экран необходимо использовать функцию printf (см. п. 4.2) (Листинг 56):
Выводимое значение вычислено во время вызова функции printf .
Вычисление определенного интеграла
Пусть необходимо вычислить определенный интеграл 
Определим функцию с именем s, которая будет задавать выражение 
—>function c=s(x), c=1((cos(x/9))^2) endfunction
Вычисление длины гипотенузы
Пусть требуется найти гипотенузу прямоугольного треугольника, если длины его катетов равны 5 и 3.
Длина гипотенузы ( с ) вычисляется по формуле 


Задание функции для вычисления логарифма с произвольным основанием
Согласно свойствам логарифма:



Для вычисления зададим функцию (см. гл. 5), аргументами которой будут основание логарифма и число, логарифм которого необходимо вычислить. Функция будет вычислять логарифм числа по произвольному основанию по формуле: 
В данном примере LOG — имя функции, osn и arg — входные параметры функции, они задают основание логарифма и число, которое необходимо прологарифмировать, соответственно.
Во второй строке Листинга 59 проведено обращение к функции LOG . Такое обращение должно привести к вычислению логарифма по основанию 3 от 9 (3 — основание логарифма, 9 — аргумент логарифма).
Видео:34 Задача: Найти корни квадратного уравнения при помощи PythonСкачать

Задания для самоконтроля
Материальная точка движется прямолинейно по закону 
Найти скорость точки в момент t =2 c (перемещение измеряется в метрах).
Найдите силу, действующую на материальную точку массой 

Вращение тела вокруг оси совершается по закону 
Материальная точка движется прямолинейно по закону 
Вычислить определенный интеграл
Сила в 4 Н растягивает пружину на 8 см. Какую работу надо произвести, чтобы растянуть пружину на 8 см?
Вычислить определенный интеграл
Определите точку пересечения касательной в точке 

Постройте график функции 

Вычислить скалярное произведение векторов, если 

Докажите, что векторы 


Решить систему уравнений:
Задать функцию для вычисления длины вектора по его координатам.
Найдите координаты вектора 




Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Глоссарий
Внешняя функция — функция, определенная для использования в различных сеансах Scilab.
Встроенная функция — функция, описание которой хранится в специальном файле (библиотеке). Этот файл подгружается автоматически при запуске Scilab.
Графический интерфейс пользователя (ГИП, англ. graphical user interface, GUI) в вычислительной технике — система средств для взаимодействия пользователя с компьютером, основанная на представлении всех доступных пользователю системных объектов и функций в виде графических компонентов экрана (окон, значков, меню, кнопок, списков и т. п.). При этом, в отличие от интерфейса командной строки, пользователь имеет произвольный доступ (с помощью клавиатуры или устройства координатного ввода типа «мышь») ко всем видимым экранным объектам.
Комментарии — пояснения к исходному тексту программы, оформленные по правилам, определяемым языком программирования. Комментарии не оказывают никакого влияния на результат работы программы.
Листинг — текст компьютерной программы или ее части, записанный на каком-либо языке программирования. Обычно данный термин употребляется для текста, распечатанного на бумаге.
Оператор (в программировании) — фраза алгоритмического языка, определяющая законченный этап обработки данных. В состав операторов входят ключевые слова, данные, выражения и др.
атомарные операторы, никакая часть которых не является самостоятельным оператором;
составные операторы, объединяющие другие операторы в новый, укрупненный оператор.
Список — упорядоченная совокупность объектов, называемых элементами списка.
Терминал — оконечная часть некой системы, которая обеспечивает связь системы с внешней средой. Терминал в Unix представляет собой системное приложение.
Функция (в языке программирования) — это заданная последовательность действий, реализующая определенный алгоритм. Определяется описанием типа результата, именем, списком формальных параметров и составным оператором, описывающим выполняемые функцией действия.
Численное дифференцирование — это вычислительная процедура определения производной в заданной точке. Простейшая идея численного дифференцирования состоит в том, что функция заменяется интерполяционным многочленом и производная функции приближенного заменяется соответствующей производной интерполяционного многочлена.
Численное интегрирование (историческое название: квадратура) — вычисление значения определенного интеграла (как правило, приближенное), основанное на том, что величина интеграла численно равна площади криволинейной трапеции, ограниченной осью абсцисс, графиком интегрируемой функции и отрезками прямых 

Видео:решаем квадратные уравнения в ExcelСкачать

Список литературы
Андриевский Б. , Фрадков А. Элементы математического моделирования в программных средах MatLab 5 и Scilab. — СПб.: Наука, 2001. — 286 с.
Алексеев Е.Р. , Чеснокова О.В. Scilab — теория и практика на русском языке / Е.Р. Алексеев, О.В. Чеснокова — 2007. — Режим доступа:
Павлова М.И. Руководство по работе с пакетом Scilab / М.И. Павлова. — Режим доступа: /
Campbell S.L. , Nikoukhah R. Auxiliary Signal Design for Failure Detection. — Cloth, 2004. — 208 p.
Bunks C . , Chancelier J.P., Delebecque F., et ab. Engineering and Scientific Computing with Scilab — Boston.: Birkhäuser, 1999. — 524 p.
Campbell S.L., Chancelier J.P., Nikoukhah R. Modeling and Simulation in Scilab/Scicos – Springer, 2005. — 313 p.
Видео:Уравнение. Практическая часть - решение задачи. 1 часть. 5 класс.Скачать

Приложение А
Оформление текста программы для определения внешней функции.
function[имя1. имяM]=имя_функции(переменная_1. переменная_N)
В данном случае имя1. имяM – список выходных параметров (от 1 до M ), то есть переменных, которым будет присвоен конечный результат вычислений, имя_функции – имя, с которым эта функция будет вызываться, переменная_1. переменная_N – входные параметры ( N параметров).
📹 Видео
5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

Введение в Scilab, лекция по программированиюСкачать

Старая вступительная задача в ОксфордСкачать

Практическая часть лабораторной работы. Компьютерное моделирование в приложении Хсоs, Scilab.Скачать

Самый простой способ решить кубическое уравнениеСкачать

Как решают уравнения в России и США!?Скачать

Комплексные корни квадратного уравненияСкачать

Сложные уравнения со скобками. Как решать уравнения в несколько действий в 5 классе.Скачать

Введение в ScilabСкачать

Математические действия над списками в Scilab.aviСкачать