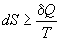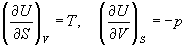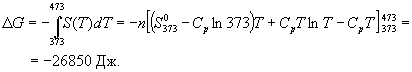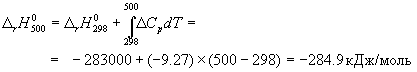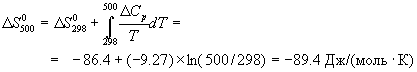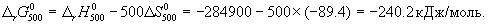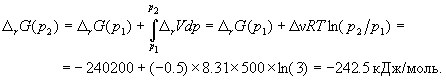Понятие энтропии
Абсолютная энтропия веществ и изменение энтропии в процессах
Стандартная энтропия
Стандартная энтропия образования
Энергия Гиббса
Стандартная энергия Гиббса образования
Энтальпийный, энтропийный фактор и направление процесса
Примеры решения задач
Задачи для самостоятельного решения
- Понятие энтропии
- Абсолютная энтропия веществ и изменение энтропии в процессах
- Стандартная энтропия
- Стандартная энтропия образования
- Энергия Гиббса
- Стандартная энергия Гиббса образования
- Энтальпийный, энтропийный фактор и направление процесса
- Примеры решения задач
- Задачи для самостоятельного решения
- Задачи к разделу Основы термодинамики с решениями
- Задачи к разделу Основы термодинамики с решениями
- Вычислить энтальпию энтропию и энергию гиббса по уравнению
- 📺 Видео
Видео:Свободная энергия Гиббса. 10 класс.Скачать

Понятие энтропии
Энтропия S – функция состояния системы. Энтропия характеризует меру неупорядоченности (хаотичности) состояния системы. Единицами измерения энтропии являются Дж/(моль·К).
Видео:Химия | Тепловой эффект химической реакции (энтальпия)Скачать

Абсолютная энтропия веществ и изменение энтропии в процессах
При абсолютном нуле температур (Т = 0 К) энтропия идеального кристалла любого чистого простого вещества или соединения равна нулю. Равенство нулю S при 0 К позволяет вычислить абсолютные величины энтропий веществ на основе экспериментальных данных о температурной зависимости теплоемкости.
Изменение энтропии в процессе выражается уравнением:
где S(прод.) и S(исх.) – соответственно абсолютные энтропии продуктов реакции и исходных веществ.
На качественном уровне знак S реакции можно оценить по изменению объема системы ΔV в результате процесса. Знак ΔV определяется по изменению количества вещества газообразных реагентов Δnг. Так, для реакции
(Δnг = 1) ΔV > 0, значит, ΔS > 0.
Видео:Решение задач на вычисление энергии Гиббса. 1 часть. 10 класс.Скачать

Стандартная энтропия
Величины энтропии принято относить к стандартному состоянию. Чаще всего значения S рассматриваются при Р = 101,325 кПа (1 атм) и температуре Т = 298,15 К (25 о С). Энтропия в этом случае обозначается S о 298 и называется стандартной энтропией при Т = 298,15 К. Следует подчеркнуть, что энтропия вещества S (S о ) увеличивается при повышении температуры.
Видео:Внутренняя энергия и энтальпия. Расчет энтальпии. Практическая часть. 10 класс.Скачать

Стандартная энтропия образования
Стандартная энтропия образования ΔS о f,298 (или ΔS о обр,298) – это изменение энтропии в процессе образования данного вещества (обычно 1 моль), находящегося в стандартном состоянии, из простых веществ, также находящихся в стандартном состоянии.
Видео:Энтальпия реакции. Решение задачи.Скачать

Энергия Гиббса
Энергия Гиббса G – функция состояния системы. Энергия Гиббса равна:
Абсолютное значение энергии Гиббса определить невозможно, однако можно вычислить изменение δG в результате протекания процесса.
Критерий самопроизвольного протекания процесса: в системах, находящихся при Р, Т = const, самопроизвольно могут протекать только процессы, сопровождающиеся уменьшением энергии Гиббса (ΔG
Видео:Тепловой эффект хим. реакции. Энтальпия. Закон Гесса. Капучинка ^-^Скачать

Стандартная энергия Гиббса образования
Стандартная энергия Гиббса образования δG о f,298 (или δG о обр,298) – это изменение энергии Гиббса в процессе образования данного вещества (обычно 1 моль), находящегося в стандартном состоянии, из простых веществ, также находящихся в стандартном состоянии, причем простые вещества пристутствуют в наиболее термодинамически устойчивых состояниях при данной температуре.
Для простых веществ, находящихся в термодинамически наиболее устойчивой форме, δG о f,298 = 0.
Видео:Внутренняя энергия и энтальпия. 10 класс.Скачать

Энтальпийный, энтропийный фактор и направление процесса
Проанализируем уравнение ΔG о Т = ΔН о Т — ΔТS о Т. При низких температурах ТΔS о Т мало. Поэтому знак ΔG о Т определяется в основном значением ΔН о Т (энтальпийный фактор). При высоких температурах ТΔS о Т – большая величина, знак Δ G о Т определяется и энтропийным фактором. В зависимости от соотношения энтальпийного (ΔН о Т) и энтропийного (ТΔS о Т) факторов существует четыре варианта процессов.
- Если ΔН о Т о Т > 0, то ΔG о Т
- Если ΔН о Т > 0, ΔS о Т о Т > 0 всегда (процесс не протекает ни при какой температуре).
- Если ΔН о Т о Т о Т о /ΔS о (процесс идет при низкой температуре за счет энтальпийного фактора).
- Если ΔН о Т > 0, ΔS о Т > 0, то ΔG о Т ΔН о / ΔS о (процесс идет при высокой температуре за счет энтропийного фактора).
Видео:Энтропия. 10 класс.Скачать

Примеры решения задач
Задача 1. Используя термодинамические справочные данные, вычислить при 298,15 К изменение энтропии в реакции:
Объяснить знак и величину ΔS о .
Решение. Значения стандартных энтропий исходных веществ и продуктов реакции приведены ниже:
| Вещество | NH3(г) | O2(г) | NО(г) | H2O(ж) |
| S о 298, Дж/(моль·К) | 192,66 | 205,04 | 210,64 | 69,95 |
В данной реакции ΔV o х.р.,298
Задача 2. Используя справочные термодинамические данные, рассчитать стандартную энтропию образования NH4NO3(к). Отличается ли стандартная энтропия образования NH4NO3(к) от стандартной энтропии этого соединения?
Решение. Стандартной энтропии образования NH4NO3 отвечает изменение энтропии в процессе:
Значения стандартных энтропий исходных веществ и продуктов реакции приведены ниже:
| Вещество | N2(г) | H2(г) | O2(г) | NH4NO3(к) |
| S о 298, Дж/(моль·К) | 191,50 | 130,52 | 205,04 | 151,04 |
Стандартная энтропия образования NH4NO3(к), равная — 609,06 Дж/(моль·К), отличается от стандартной энтропии нитрата аммония S о 298(NH4NO3(к)) = +151,04 Дж/(моль·К) и по величине, и по знаку. Следует помнить, что стандартные энтропии веществ S о 298 всегда больше нуля, в то время как величины ΔS 0 f,298, как правило, знакопеременны.
Задача 3. Изменение энергии Гиббса реакции:
равно δG о 298= –474,46 кДж. Не проводя термодинамические расчеты, определить, за счет какого фактора (энтальпийного или энтропийного) протекает эта реакция при 298 К и как будет влиять повышение температуры на протекание этой реакции.
Решение. Поскольку протекание рассматриваемой реакции сопровождается существенным уменьшением объема (из 67,2 л (н.у.) исходных веществ образуется 36 мл жидкой воды), изменение энтропии реакции ΔS о о 298 реакции меньше нуля, то она может протекать при температуре 298 К только за счет энтальпийного фактора. Повышение температуры уменьшает равновесный выход воды, поскольку ТΔS о
Задача 4. Используя справочные термодинамические данные, определить может ли при 298,15 К самопроизвольно протекать реакция:
Если реакция не будет самопроизвольно протекать при 298,15 К, оценить возможность ее протекания при более высоких температурах.
Решение. Значения стандартных энергий Гиббса и энтропий исходных веществ и продуктов реакции приведены ниже:
| Вещество | С4Н10(г) | С2Н4(г) | Н2(г) |
| ΔG о f,298× , кДж/моль | — 17,19 | 68,14 | 0 |
| S о 298, Дж/(моль·К) | 310,12 | 219,45 | 130,52 |
ΔG о х.р.,298 > 0, следовательно, при Т = 298,15 К реакция самопроизвольно протекать не будет.
Поскольку ΔS о х.р.,298 > 0, то при температуре Т>ΔН о /ΔS о величина ΔG о х.р.,298 станет величиной отрицательной и процесс сможет протекать самопроизвольно.
Задача 5. Пользуясь справочными данными по ΔG о f,298 и S о 298, определите ΔH о 298 реакции:
Решение. Значения стандартных энергий Гиббса и энтропий исходных веществ и продуктов реакции приведены ниже:
| Вещество | N2O(г) | H2(г) | N2H4(г) | H2O(ж) |
| ΔG о f,298, кДж/моль | 104,12 | 0 | 159,10 | -237,23 |
| S о 298, Дж/(моль·К) | 219,83 | 130,52 | 238,50 | 69,95 |
ΔG о 298 = ΔН о 298 – ТΔS о 298. Подставляя в это уравнение величины ΔН о 298 и ТΔS о 298, получаем:
ΔН о 298 = –182,25× 10 3 + 298·(–302,94) = –272526,12 Дж = – 272,53 кДж.
Следует подчеркнуть, что поскольку ΔS о 298 выражена в Дж/(моль× К), то при проведении расчетов ΔG 0 298 необходимо также выразить в Дж или величину ΔS 0 298 представить в кДж/(мольK).
Видео:Свободная энергия Гиббса и самопроизвольные реакции (видео 8) | Энергия| БиологияСкачать

Задачи для самостоятельного решения
1. Используя справочные данные, определите стандартную энтропию образования ΔS о f,298 NaHCO3(к).
2. Выберите процесс, изменение энергии Гиббса которого соответствует стандартной энергии Гиббса образования NO2(г):
Видео:Что такое Энтропия?Скачать

Задачи к разделу Основы термодинамики с решениями
Здесь вы найдете примеры задач на вычисление таких термодинамических параметров как энтальпия, энтропия, энергия Гиббса. Определение возможности самопроизвольного протекания процесса, а также составление термохимических уравнений.
Видео:Энергия Гиббса. Практическая часть. 10 класс.Скачать

Задачи к разделу Основы термодинамики с решениями
Задача 1. Рассчитайте стандартную энтальпию и стандартную энтропию химической реакции. Определите в каком направлении при 298 °К (прямом или обратном) будет протекать реакция. Рассчитайте температуру, при которой равновероятны оба направления реакции.
Fe2O3 (к) + 3H2 = 2Fe(к) + 3H2O(г)
Используя справочные данные стандартных энтальпий веществ, находим:
Используя справочные данные стандартных энтропий веществ, находим:
При Т=298°К, ΔG > 0 – реакция не идет самопроизвольно, т.е. реакция будет протекать в обратном направлении.
Чтобы рассчитать температуру, при которой равновероятны оба направления реакции, надо ΔG приравнять к нулю:
При Т = 705,83 К реакция будет идти равновероятно как в прямом так и в обратном направлении.
Задача 2. Вычислите энергию Гиббса и определите возможность протекания реакции при температурах 1000 и 3000 К.
| Cr2O3 (т) + 3C (т) = 2Cr (т) + 3CO (г) | ||||
| ΔH298, кДж/моль | — 1141 | 0 | 0 | — 110,6 |
| ΔS298, Дж/(моль×К) | 81,2 | 5,7 | 23,6 | 197,7 |
Вычисления энергии Гиббса проводим согласно выражению:
Необходимо рассчитать энтальпию и энтропию химической реакции.
Используя справочные данные стандартных энтальпий веществ, находим:
Аналогично, используя справочные данные стандартных энтропий веществ, находим:
Найдем энергию Гиббса при 1000 К
ΔG1000 > 0, следовательно, реакция самопроизвольно не идет.
Найдем энергию Гиббса при 3000 К
ΔG3000 ˂ 0, следовательно, реакция протекает самопроизвольно.
Задача 3. Определите тепловой эффект сгорания жидкого CS2(ж) до образования газообразных СО2 и SO2. Сколько молей CS2 вступят в реакцию, если выделится 700 кДж тепла?
Уравнение реакции сгорания жидкого сероуглерода следующее:
Тепловой эффект реакции вычислим подставляя справочные данные стандартных энтальпий веществ в выражение:
Т.е. при сгорании 1 моля сероуглерода выделяется 1075,1 кДж тепла
а при сгорании x молей сероуглерода выделяется 700 кДж тепла
Найдем х:
x = 700·1/1075,1 = 0,65 моль
Итак, если в результате реакции выделится 700 кДж тепла, то в реакцию вступят 0,65 моль CS2
Задача 4. Вычислите тепловой эффект реакции восстановления оксида железа (II) водородом, исходя из следующих термохимических уравнений:
1. FeO (к) + CO (г) = Fe (к) + CО2 (г); ΔH1 = -18,20 кДж;
2. СO (г) + 1/2O2 (г) = СO2 (г) ΔН2 = -283,0 кДж;
3. H2 (г) + ½ O2 (г) = H2O (г) ΔН3 = -241,83 кДж.
Реакция восстановления оксида железа (II) водородом имеет следующий вид:
4. FeO (к) + H2 (г) = Fe (к) + H2O (г)
Чтобы вычислить тепловой эффект реакции необходимо применить закон Гесса, т.е. реакцию 4. можно получить, если сложить реакции 1. и 2. и вычесть реакцию 1.:
Таким образом, тепловой эффект реакции восстановления оксида железа (II) водородом равен
Задача 5. Реакция горения бензола выражается термохимическим уравнением:
С6Н6(ж) + 7½ О2(г) = 6СО2(г) + 3Н2О(г) – 3135,6 кДж.
Вычислите теплоту образования жидкого бензола. Определите теплотворную способность жидкого бензола при условии, что стандартные условия совпадают с нормальными.
Тепловой эффект реакции равен:
В нашем случае ΔHр-ции = – 3135,6 кДж, найдем теплоту образования жидкого бензола:
Теплотворная способность жидкого бензола вычисляется по формуле:
М(бензола) = 78 г/моль
QТ = – 3135,6· 1000 / 78 = — 4,02·10 4 кДж/кг
Теплотворная способность жидкого бензола QТ = — 4,02·10 4 кДж/кг
Задача 6. Реакция окисления этилового спирта выражается уравнением:
С2Н5ОН(ж) + 3,0 О2(г) = 2СО2(г) + 3Н2О(ж).
Определить теплоту образования С2Н5ОН(ж), зная ΔН х.р. = — 1366,87 кДж. Напишите термохимическое уравнение. Определите мольную теплоту парообразования С2Н5ОН(ж) → С2Н5ОН(г), если известна теплота образования С2Н5ОН(г), равная –235,31 кДж·моль -1 .
Исходя из приведенных данных, запишем термохимическое уравнение:
Тепловой эффект реакции равен:
Используя справочные данные теплот образования веществ, найдем теплоту образования С2Н5ОН(ж):
ΔH 0 C2H5OH(ж) = -277,36 кДж/моль
ΔH 0 парообразования = — 235,31 + 277,36 = 42,36 кДж/моль
Мы определили, что теплота образования С2Н5ОН(ж) равна
ΔH 0 C2H5OH(ж) = -277,36 кДж/моль
ΔH 0 парообразования = 42,36 кДж/моль
Задача 7. Чем можно объяснить, что при стандартных условиях, невозможна экзотермическая реакция:
СО2 (г)+Н2 (г) ↔ СО (г)+Н2О (ж)?
Рассчитайте ΔG данной реакции. При каких температурах данная реакция становится самопроизвольной?
Рассчитаем ΔG данной реакции:
Для этого сначала определим ΔH и ΔS реакции:
Используя справочные данные стандартных энтальпий веществ, находим:
Аналогично, используя справочные данные стандартных энтропий веществ, находим:
Найдем энергию Гиббса при стандартных условиях
следовательно, реакция самопроизвольно не идет.
Найдем при каких температурах данная реакция становится самопроизвольной.
В состоянии равновесия ΔGр-ции= 0, тогда
Задача 8. Рассчитав на основании табличных данных ΔG и ΔS, определите тепловой эффект реакции:
2 NO (г) + Cl2 (г) ↔ 2 NOCl(г).
При постоянных температуре и давлении, изменение энергии Гиббса связано с энтальпией и энтропией выражением:
На основании табличных данных рассчитаем ΔG и ΔS
ΔH = — 40,64 + 298 · (-121,04/1000) = — 76,7 кДж/моль
Тепловой эффект реакции ΔH = — 76,7 кДж/моль
Задача 9. С чем будет более интенсивно взаимодействовать газообразный хлористый водород (в расчете на 1 моль): с алюминием или с оловом? Ответ дайте, рассчитав ΔG 0 обеих реакций. Продуктами реакций являются твердая соль и газообразный водород.
Рассчитаем ΔG 0 для реакции взаимодействия газообразного хлористого водорода (в расчете на 1 моль) с алюминием
В реакции принимает участие 2 моль Al(т), тогда ΔGр-ции1 1 моля Al(т) равно
ΔG 0 р-ции 1 = -701,98 / 2 = -350,99 кДж/моль
Рассчитаем ΔG 0 для реакции взаимодействия газообразного хлористого водорода (в расчете на 1 моль) с оловом:
ΔG 0 р-ции 2 = -288,4 + 0- 0- 2·(-95,27) = -97,86 кДж/моль
Задача 10. Не прибегая к вычислениям, определите, какие знаки (>0, 0.
Видео:ЭнтальпияСкачать

Вычислить энтальпию энтропию и энергию гиббса по уравнению
Термодинамическими потенциалами, или характеристическими функциями, называют термодинамические функции, которые содержат в себе всю термодинамическую информацию о системе. Наибольшее значение имеют четыре основных термодинамических потенциала:
В скобках указаны термодинамические параметры, которые получили название естественных переменных для термодинамических потенциалов. Все эти потенциалы имеют размерность энергии и все они не имеют абсолютного значения, поскольку определены с точностью до постоянной, которая равна внутренней энергии при абсолютном нуле.
Зависимость термодинамических потенциалов от их естественных переменных описывается основным уравнением термодинамики, которое объединяет первое и второе начала. Это уравнение можно записать в четырех эквивалентных формах:
Эти уравнения записаны в упрощенном виде — только для закрытых систем, в которых совершается только механическая работа.
Зная любой из четырех потенциалов как функцию естественных переменных, можно с помощью основного уравнения термодинамики найти все другие термодинамические функции и параметры системы (см. пример 5-1).
Другой важный смысл термодинамических потенциалов состоит в том, что они позволяют предсказывать направление термодинамических процессов. Так, например, если процесс происходит при постоянных температуре и давлении, то неравенство, выражающее второй закон термодинамики:
эквивалентно неравенству dGp,T 0 (мы учли, что при постоянном давлении Qp = dH), где знак равенства относится к обратимым процессам, а неравенства — к необратимым. Таким образом, при необратимых процессах, протекающих при постоянных температуре и давлении, энергия Гиббса всегда уменьшается. Минимум энергии Гиббса достигается при равновесии.
Аналогично, любой термодинамический потенциал в необратимых процессах при постоянстве естественных переменных уменьшается и достигает минимума при равновесии:
Потенциал
Естественные
переменные
Условие само-произвольности
Условия
равновесия
S = const, V = const
dU 2 U > 0
S = const, p = const
dH 2 H > 0
T = const, V = const
dF 2 F > 0
T = const, p = const
dG 2 G > 0
Наибольшее значение в конкретных термодинамических расчетах имеют два последние потенциала — энергия Гельмгольца F и энергия Гиббса G , т.к. их естественные переменные наиболее удобны для химии. Другое (устаревшее) название этих функций — изохорно-изотермический и изобарно-изотермический потенциалы. Они имеют дополнительный физико-химический смысл. Уменьшение энергии Гельмгольца в каком-либо процессе при T = const, V = const равно максимальной механической работе, которую может совершить система в этом процессе:
Таким образом, энергия F равна той части внутренней энергии (U = F + TS), которая может превратиться в работу.
Аналогично, уменьшение энергии Гиббса в каком-либо процессе при T = const, p = const равно максимальной полезной (т.е., немеханической) работе, которую может совершить система в этом процессе:
Зависимость энергии Гельмгольца (Гиббса) от объема (давления) вытекает из основного уравнения термодинамики (5.3), (5.4):
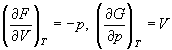
Зависимость этих функций от температуры можно описать с помощью основного уравнения термодинамики:
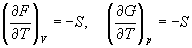
или с помощью уравнения Гиббса-Гельмгольца:
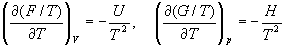
Расчет изменения функций F и G в химических реакциях можно проводить разными способами. Рассмотрим два из них на примере энергии Гиббса.
1) По определению, G = H — TS. Если продукты реакции и исходные вещества находятся при одинаковой температуре, то стандартное изменение энергии Гиббса в химической реакции равно:
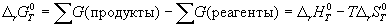
где тепловой эффект можно рассчитать с помощью стандартных энтальпий образования, а стандартное изменение энтропии — по абсолютным энтропиям участников реакции.
2) Аналогично тепловому эффекту реакции, изменение энергии Гиббса можно рассчитать, используя энергии Гиббса образования веществ:

В термодинамических таблицах обычно приводят абсолютные энтропии и значения термодинамических функций образования соединений из простых веществ при температуре 298 К и давлении 1 бар (стандартное состояние). Для расчета rG и rF при других условиях используют соотношения (5.5) — (5.7).
Все термодинамические потенциалы являются функциями состояния. Это свойство позволяет найти некоторые полезные соотношения между частными производными, которые называют соотношениями Максвелла.
Рассмотрим выражение (5.1) для внутренней энергии. Т.к. dU — полный дифференциал, частные производные внутренней энергии по естественным переменным равны:
Если продифференцировать первое тождество по объему, а второе — по энтропии, то получатся перекрестные вторые частные производные внутренней энергии, которые равны друг другу:
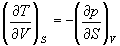
Три другие соотношения получаются при перекрестном дифференцировании уравнений (5.2) — (5.4).
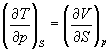
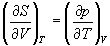
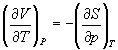
ПРИМЕРЫ
Пример 5-1. Внутренняя энергия некоторой системы известна как функция энтропии и объема, U(S,V). Найдите температуру и теплоемкость этой системы.
Решение. Из основного уравнения термодинамики (5.1) следует, что температура — это частная производная внутренней энергии по энтропии:
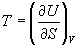
Изохорная теплоемкость определяет скорость изменения энтропии с температурой:
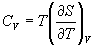
Воспользовавшись свойствами частных производных, можно выразить производную энтропии по температуре через вторую производную внутренней энергии:
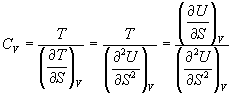
Пример 5-2. Используя основное уравнение термодинамики, найдите зависимость энтальпии от давления при постоянной температуре: а) для произвольной системы; б) для идеального газа.
Решение. а) Если основное уравнение в форме (5.2) поделить на dp при постоянной температуре, получим:
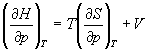
Производную энтропии по давлению можно выразить с помощью соотношения Максвелла для энергии Гиббса (5.13):
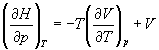
б) Для идеального газа V(T) = nRT / p. Подставляя эту функцию в последнее тождество, получим:
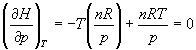
Энтальпия идеального газа не зависит от давления.
Пример 5-3. Выразите производные 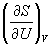
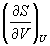
Решение. Основное уравнение термодинамики (5.1) можно переписать в виде:
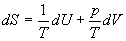
представив энтропию как функцию внутренней энергии и объема. Коэффициенты при dU и dV равны соответствующим частным производным:
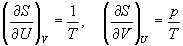
Пример 5-4. Два моля гелия (идеальный газ, мольная теплоемкость Cp = 5/2 R) нагревают от 100 о С до 200 о С при p = 1 атм. Вычислите изменение энергии Гиббса в этом процессе, если известно значение энтропии гелия, 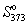
Решение. Изменение энергии Гиббса при нагревании от 373 до 473 К можно найти, проинтегрировав частную производную по температуре (5.6):
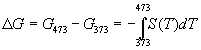
Зависимость энтропии от температуры при постоянном давлении определяется изобарной темлоемкостью:
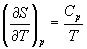
Интегрирование этого выражения от 373 К до T дает:
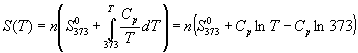
Подставляя это выражение в интеграл от энтропии, находим:
Процесс нагревания не обязан быть самопроизвольным, т.к. уменьшение энергии Гиббса служит критерием самопроизвольного протекания процесса только при T = const и p = const.
Ответ. G = -26850 Дж.
Пример 5-5. Рассчитайте изменение энергии Гиббса в реакции
при температуре 500 K и парциальных давлениях 3 бар. Будет ли эта реакция самопроизвольной при данных условиях? Газы считать идеальными. Необходимые данные возьмите из справочника.
Решение. Термодинамические данные при температуре 298 К и стандартном давлении 1 бар сведем в таблицу:
Вещество
Энтальпия образования 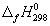
Энтропия 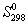
Теплоемкость 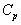
Реакция
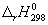
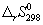
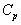
CO + ЅO2 =
= CO2
Примем, что Cp = const. Изменения термодинамических функций в результате реакции рассчитаны как разность функций реагентов и продуктов:
f = f(CO2) — f(CO) — Ѕ f(O2).
Стандартный тепловой эффект реакции при 500 К можно рассчитать по уравнению Кирхгофа в интегральной форме (3.8):
Стандартное изменение энтропии в реакции при 500 К можно рассчитать по формуле (4.9):
Стандартное изменение энергии Гиббса при 500 К:
Для расчета изменения энергии Гиббса при парциальных давлениях 3 атм необходимо проинтегрировать формулу (5.5) и использовать условие идеальности газов ( V = n RT / p, n — изменение числа молей газов в реакции):
Эта реакция может протекать самопроизвольно при данных условиях.
Ответ. G = -242.5 кДж/моль.
ЗАДАЧИ
5-1. Выразите внутреннюю энергию как функцию переменных G, T, p.
5-2. Используя основное уравнение термодинамики, найдите зависимость внутренней энергии от объема при постоянной температуре: а) для произвольной системы; б) для идеального газа.
5-3. Известно, что внутренняя энергия некоторого вещества не зависит от его объема. Как зависит давление вещества от температуры? Ответ обоснуйте.
5-4. Выразите производные 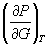
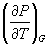
5-5. Напишите выражение для бесконечно малого изменения энтропии как функции внутренней энергии и объема. Найдите частные производные энтропии по этим переменным и составьте соответствующее уравнение Максвелла.
5-6. Для некоторого вещества известно уравнение состояния p(V, T). Как изменяется теплоемкость Cv с изменением объема? Решите задачу: а) в общем виде; б) для какого-либо конкретного уравнения состояния (кроме идеального газа).
5-7. Докажите тождество: 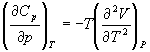
5-8. Энергия Гельмгольца одного моля некоторого вещества записывается следующим образом:
где a, b, c, d — константы. Найдите давление, энтропию и теплоемкость CV этого тела. Дайте физическую интерпретацию константам a, b, d.
5-9. Нарисуйте график зависимости энергии Гиббса индивидуального вещества от температуры в интервале от 0 до T > Tкип.
5-10. Для некоторой системы известна энергия Гиббса:
5-11. Зависимость мольной энергии Гельмгольца некоторой системы от температуры и объема имеет вид:
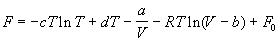
где a, b, c, d — константы. Выведите уравнение состояния p(V,T) для этой системы. Найдите зависимость внутренней энергии от объема и температуры U(V,T). Каков физический смысл постоянных a, b, c?
5-12. Найдите зависимость мольной внутренней энергии от объема для термодинамической системы, которая описывается уравнением состояния (для одного моля)
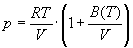
где B(T) — известная функция температуры.
5-13. Для некоторого вещества зависимость теплоемкости от температуры имеет вид: CV = aT 3 при температуре 0 — 10 К. Найдите зависимость энергии Гельмгольца, энтропии и внутренней энергии от температуры в этом диапазоне.
5-14. Для некоторого вещества зависимость внутренней энергии от температуры имеет вид: U = aT 4 + U0 при температуре 0 — 10 К. Найдите зависимость энергии Гельмгольца, энтропии и теплоемкости CV от температуры в этом диапазоне.
5-15. Выведите соотношение между теплоемкостями:
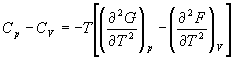
5-16. Исходя из тождества 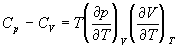
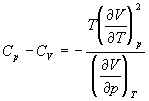
5-17. Один моль газа Ван-дер-Ваальса изотермически расширяется от объема V1 до объема V2 при температуре T. Найдите U, H, S, F и G для этого процесса.
5-18. Вычислите изменение H, U, F, G, S при одновременном охлаждении от 2000 К до 200 К и расширении от 0.5 м 3 до 1.35 м 3 0.7 молей азота (CV = 5/2 R). Энтропия газа в исходном состоянии равна 150 Дж/(моль . К), газ можно считать идеальным.
5-19. Вычислите изменение энергии Гиббса при сжатии от 1 атм до 3 атм при 298 К: а) одного моля жидкой воды; б) одного моля водяного пара (идеальный газ).
5-20. Изменение энергии Гиббса в результате испарения воды при 95 о С и 1 атм равно 546 Дж/моль. Рассчитайте энтропию паров воды при 100 о С, если энтропия жидкой воды равна 87.0 Дж/(моль . К). При каком давлении изменение энергии Гиббса в результате испарения воды будет равно 0 при 95 о С?
5-21*. Давление над одним молем твердой меди при температуре 25 о С увеличили от 1 до 1000 атм. Найти U, H, S, F. Медь считать несжимаемой, плотность 8.96 г/см 3 , изобарический коэффициент теплового расширения 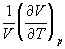
5-22. Вычислите стандартную энергию Гиббса образования (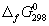
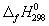
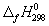
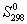
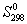
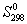
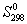
5-23. Рассчитайте G o при 25 о С для химической реакции:
Стандартные значения энтальпии образования и абсолютной энтропии при 25 о С равны: fH o (HСl) = -22.1 ккал/моль, fH o (H2O(ж)) = -68.3 ккал/моль; S o (HCl) = 44.6 кал/(моль . K), S o (O2) = 49.0 кал/(моль . K), S o (Сl2) = 53.3 кал/(моль . K), S o (H2O(ж)) = 16.7 кал/(моль . K).
5-24. Рассчитайте G o при 25 о С для химической реакции:
Стандартные значения энтальпии образования и абсолютной энтропии при 25 о С равны: fH o (СO2) = -94.1 ккал/моль, fH o (СH4) = -17.9 ккал/моль, fH o (H2O(ж)) = -68.3 ккал/моль; S o (СO2) = 51.1 кал/(моль . K), S o (H2) = 31.2 кал/(моль . K), S o (СH4) = 44.5 кал/(моль . K), S o (H2O(ж)) = 16.7 кал/(моль . K).
5-25. Рассчитайте стандартные энергии Гиббса и Гельмгольца G o и F o при 300 о С для химической реакции:
Может ли эта реакция протекать самопроизвольно при данной температуре? Теплоемкости веществ считать постоянными.
5-26. Найдите энергию Гиббса образования NH3 при температурах 298 и 400 K, если известны следующие данные: 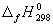
NH3
35.7
 , Дж/(моль . К)
, Дж/(моль . К)Считать, что теплоемкости в указанном интервале температур постоянны.
5-27. Рассчитайте стандартные энергии Гиббса и Гельмгольца G o и F o при 60 о С для химической реакции:
Может ли эта реакция протекать самопроизвольно при данной температуре? Теплоемкости веществ считать постоянными.
5-28. Рассчитайте стандартные энергии Гиббса и Гельмгольца G o и F o при 700 о С для химической реакции:
Может ли эта реакция протекать самопроизвольно при данной температуре? Теплоемкости веществ считать постоянными.


Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору
📺 Видео
Энергия ГиббсаСкачать

2 4 Свободная энергия ГиббсаСкачать

Закон Гесса. 10 класс.Скачать

Решение задач на вычисление энергии Гиббса. 2 часть. 10 класс.Скачать
Решение задач на термохимические уравнения. 8 класс.Скачать

Термодинамика. Решение задач. Энтальпия, энтропия, энергия ГиббсаСкачать

Как рассчитать стандартную энтальпию образования вещества | Физическая химияСкачать

Пример свободной энергии ГиббсаСкачать