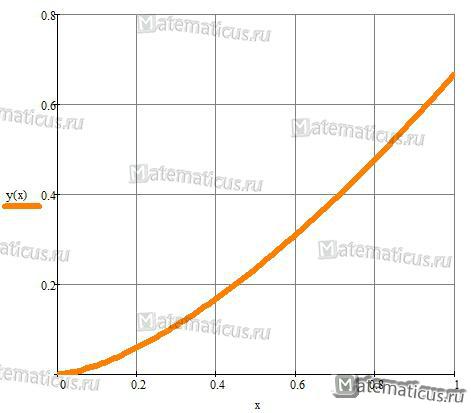
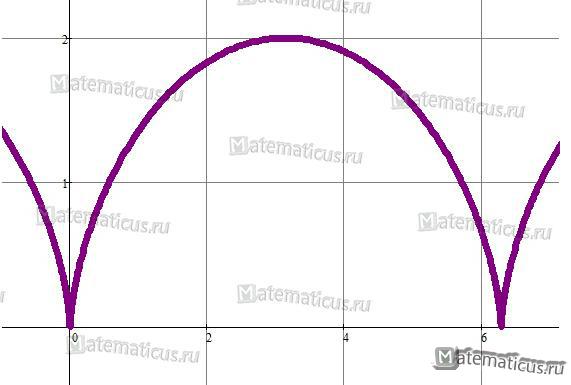
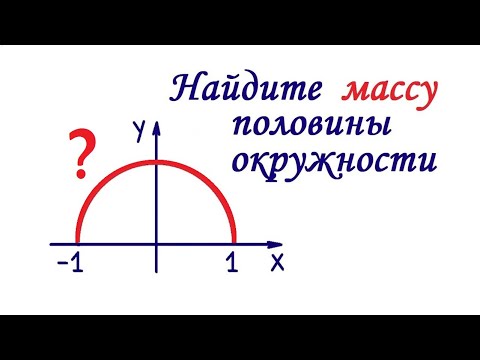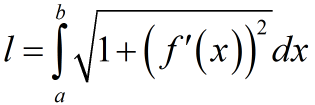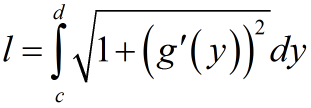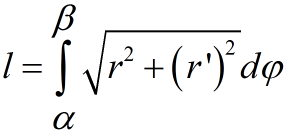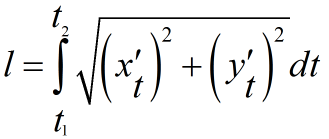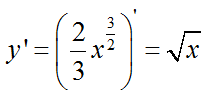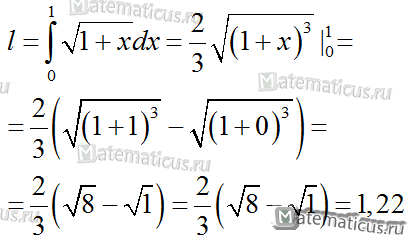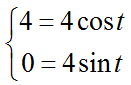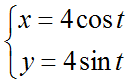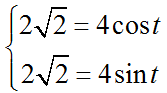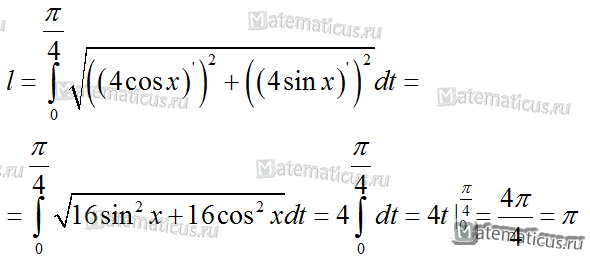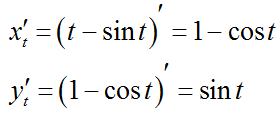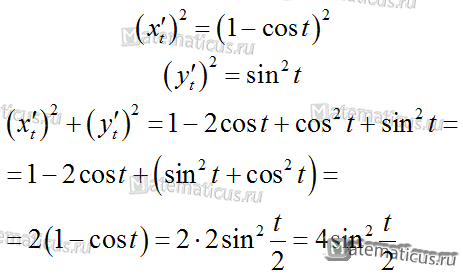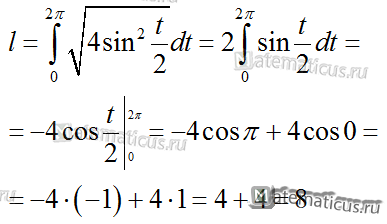Вычислить длину дуги линии заданной уравнением (2 видео)

Калькулятор длины дуги кривой линии в декартовых координатах

Одним из приложений определенного интеграла является вычисление длины дуги плоской кривой. На рисунке изображен график функции :

Для того, чтобы узнать длину дуги кривой линии изображенной на рисунке, необходимо вычислить определенный интеграл:

В более общем случае, если у нас задана функция в декартовых координатах и стоит задача найти длину дуги этой кривой между точками и , нам необходимо вычислить интеграл:

В приведенной выше формуле, выражение означает, что сначала нужно вычислить производную функции , а затем полученное выражение возвести в квадрат.

Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha, позволяет вычислить длину кривой, заданной в декартовых координатах для любой, даже очень сложной функции.

Содержание

Как найти длину дуги кривой с помощью интеграла
Вычисление длины дуги кривой, заданной в прямоугольных координатах
Вычисление длины дуги кривой, заданной параметрически
Вычисление длины дуги кривой, заданной в полярных координатах
Вычисление длины дуги
One comment
💡 Видео

Видео:Нахождение длины дуги кривой.Скачать

Как найти длину дуги кривой с помощью интеграла

Задачи на вычисление длины дуги кривой — однотипные. Существуют чёткие схемы для решения таких задач по формулам, которые отличаются в зависимости от того, какими и сколькими уравнениями задана кривая. Формулы представляют собой интегралы от корня, под которым в тех или иных сочетаниях присутствуют производные функций, которыми задана кривая. Следовательно, для того, чтобы вычислять длину дуги кривой, требуется уметь вычислять производные и интегралы. При вычислении интегралов возможны типичные трудности, связанные, например, с выбором подходящей подстановки. Эти задачи будем решать в примерах к данному уроку.

Видео:Нахождение длины дуги кривойСкачать

Вычисление длины дуги кривой, заданной в прямоугольных координатах

Пусть в прямоугольных координатах на плоскости уравнением y = f(x) задана кривая.

Найдём длину дуги AB этой кривой, заключённой между вертикальными прямыми x = a и x = b (рисунок ниже).

Возьмём на дуге AB точки A, M 1 , M 2 , . M i , . B с абсциссами x 0 = a, x 1 , x 2 , . x i , . b = x n и проведём хорды AM 1 , M 1 M 2 , . M n-1 B , длины которых обозначим соответственно через Δs 1 , Δs 2 , . Δs n . Тогда получим ломаную AM 1 M 2 . M n-1 B , вписанную в дугу AB. Длина ломаной равна

Длиной s дуги AB называется тот предел, к которому стремится длина вписанной ломаной, когда длина её наибольшего звена стремится к нулю:

Этот предел интегральной суммы равен определённому интегралу

(1).

Формула выше и есть формула для вычисления дуги кривой.

Пример 1. Найти длину дуги кривой , если .

Решение. Находим производную данной функции:

Используем формулу (1), подставляя найденную производную:

Ответ: длина дуги кривой равна 74.

Пример 2. Найти длину окружности .

Решение. Вычислим сначала длину четвёртой части окружности, лежащей в первом квадранте. Тогда уравнение дуги будет:

откуда находим производную функции:

Используем формулу (1) подставляя в неё производную, получаем:

Ответ: длина всей окружности равна .

Если в прямоугольных координатах уравнениями z = x(x) и y = y(x) задана пространственная кривая, то длина её дуги вычисляется по формуле:

. (2)

Видео:Видеоурок "Длина дуги кривой"Скачать

Вычисление длины дуги кривой, заданной параметрически

Найдём теперь длину дуги кривой в том случае, когда кривая задана параметрическими уравнениями:

В этом случае длину дуги кривой следует находить по формуле

(3).

Пример 3. Найти длину дуги кривой, заданной параметрическими уравнениями

если .

Решение. Рассчитаем интервал, в котором будет меняться значение t, если :

Вычислим производные функций x и y:

Используем формулу (3):

Ответ: длина дуги кривой равна 26.

Если параметрическими уравнениями

задана пространственная кривая, то длина её дуги вычисляется по формуле:

. (4)

Пример 4. Найти длину дуги винтовой линии, заданной параметрическими уравнениями

Решение. Вычислим производные функций x, y и z:

Используем формулу (4):

Видео:Как брать неберущийся интеграл Задача Найти длину дуги параболыСкачать

Вычисление длины дуги кривой, заданной в полярных координатах

Пусть кривая задана в полярных координатах:

Длина её дуги вычисляется по формуле:

(5).

Пример 5. Найти длину дуги кривой, заданной в полярных координатах .

Решение. Вычислим производную функции:

Заданная кривая — кардиоида (рисунок выше). Так как она симметрична, вычислим только ту часть длины дуги, у которой и и умножим её на 2. Используем формулу (5):

Видео:Вычисление длины дугиСкачать

Вычисление длины дуги

Формула для вычисления длины дуги кривой заданной уравнением у=f(x) в прямоугольной системе координат:

a — начала дуги по оси OX;

b — конец дуги по оси OX a

Если плоская кривая задана уравнением x=g(y) то формула имеет вид:

c — начала дуги по оси OY;

d — конец дуги по оси OY a

Если кривая задана в полярных координатах r=r(φ), α≤φ≤β, то длина дуги вычисляется по формуле:

Если кривая задана параметрическим уравнением вида x=x(t) и y=y(t), то длина дуги определяется по формуле

t₂, t₁ — значения параметров, которые соответствуют концам дуги t₁

Найти длину дуги функции на промежутке от 0 до 1.

Найдем производную функции:

Возведём в квадрат функцию:

Подставляя в формулу, найдем длину дуги:

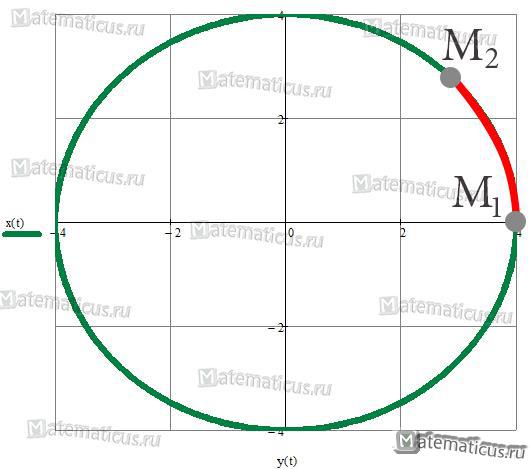
Найти длину дуги окружности от точки $left( right)$ до точки $left( right)$. Уравнение окружности задано в параметрическом виде.

Найдем параметр t в точках M₁ и M₂, решим системы уравнений.

Здесь t₁=0

Подставляя в формулу, найдем длину дуги окружности.

Вычислить длину дуги одного лепестка циклоиды. Уравнение циклоиды задано параметрическим уравнением.

Продифференцируем по t параметрические уравнения циклоиды:

Подставляя в формулу, получаем

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.3 / 5. Количество оценок: 4

Оценок пока нет. Поставьте оценку первым.

Видео:Астроида: найдем площадь и длину через определенный интегралСкачать

One comment

Была бы оценка 5, если бы не дурак, который не от большого ума изукрасил весь текст, особенно формулы и ответы, серыми узорами! Сколько времени и усилий ушло на расшифровку ответов! Так что 3,5 балла — это ещё слишком много! Так и передайте идеологу этой мазни!