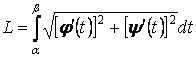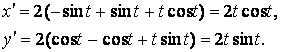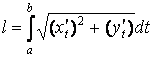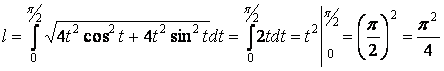Одним из приложений определенного интеграла является вычисление длины дуги плоской кривой. На рисунке изображен график функции :
Для того, чтобы узнать длину дуги кривой линии изображенной на рисунке, необходимо вычислить определенный интеграл:
В более общем случае, если у нас задана функция в декартовых координатах и стоит задача найти длину дуги этой кривой между точками и , нам необходимо вычислить интеграл:
В приведенной выше формуле, выражение означает, что сначала нужно вычислить производную функции , а затем полученное выражение возвести в квадрат.
Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha, позволяет вычислить длину кривой, заданной в декартовых координатах для любой, даже очень сложной функции.
Видео:Видеоурок "Длина дуги кривой"Скачать
Вычислить длину дуг кривых заданных параметрическими уравнениями онлайн калькулятор
        Пусть кривая задана уравнениями в параметрической форме
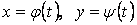
где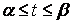     
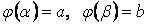
    и     
    .
        Длина дуги кривой
        Прежде, чем Вы начнёте скачивать свои варианты, попробуйте найти интеграл по образцу, приведённому ниже для варианта 27.
        Вариант 1     Вариант 2     Вариант 3     Вариант 4     Вариант 5     Вариант 6
        Вариант 7     Вариант 8     Вариант 9     Вариант 10     Вариант 11     Вариант 12
    Вариант 13     Вариант 14     Вариант 15     Вариант 16     Вариант 17     Вариант 18
    Вариант 19     Вариант 20     Вариант 21     Вариант 22     Вариант 23     Вариант 24
    Вариант 25     Вариант 26     Вариант 27     Вариант 28     Вариант 29     Вариант 30
        Задача 18.27. Вычислить длину дуги кривой, заданной параметрическими уравнениями.
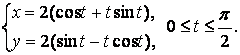
Решение
        Найдём производные
        Длина дуги кривой, заданной параметрически, ищется по формуле
        Подставляя данные, получим
        Ответ: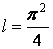     
    .
Видео:Длина дуги кривойСкачать
Вычислить длину дуг кривых заданных параметрическими уравнениями онлайн калькулятор
Построим график параметрической функции x=x(t) и y=y(t), которая задаёт прямую или кривую линию,
где параметр t лежит в промежутке [a, b],
и вы можете указать свои границы.
Задайте также функции x и y, зависящих от параметра.
Видео:14. Что такое параметрически заданная функция, производная параметрически заданной функции.Скачать
Примеры кривых
| Название кривой | Уравнение |
|---|---|
| Окружность | |
| Спираль | |
| Дельтоида | |
| Астроида | |
| Гипоциклоиды | |
| Кардиоида | |
| Нефроида | |
| Эпициклоиды | |
| Бабочка | |
| Фигуры Лиссажу | |
| Сердце |
Правила ввода выражений и функций
3.14159.. e Число e — основание натурального логарифма, примерно равно
2,7183.. i Комплексная единица oo Символ бесконечности — знак для бесконечности
© Контрольная работа РУ — калькуляторы онлайн
Видео:Астроида: найдем площадь и длину через определенный интегралСкачать
Где учитесь?
Для правильного составления решения, укажите:
🌟 Видео
Длина окружности. Математика 6 класс.Скачать
Нахождение длины дуги кривойСкачать
Длина дуги кривой| Урок 1| Надежда Павловна МедведеваСкачать
Вычисление длины дуги кривой в параметрических и полярных координатах. Вычисление объема тела.Скачать
Длина параболы и спирали Архимеда: что у них общего?Скачать
Интегралы №12 Вычисление площадейСкачать
Вычисление длины дугиСкачать
Как брать неберущийся интеграл Задача Найти длину дуги параболыСкачать
Нахождение длины дуги кривой.Скачать
ДЛИНА ДУГИ окружности 9 класс Атанасян 1111 1112 длина окружностиСкачать
Кривизна кривой, заданной параметрическиСкачать
Вычисление длины кривой и разбор задач Часть 2Скачать
Длина дуги части кривойСкачать
Математика без Ху!ни. Определенные интегралы, часть 3. Площадь фигуры.Скачать
Длина дуги окружности. 9 класс.Скачать
Построение кривой в полярной системе координатСкачать
