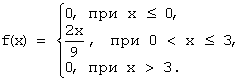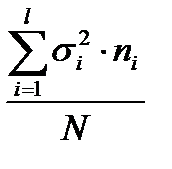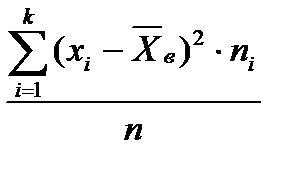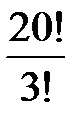ЗАДАЧИ ИЗ ТЕСТОВ С РЕШЕНИЯМИ
Задача 1. Из урны, в которой находятся 12 белых и 10 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет черным, равна…
Воспользуемся формулой 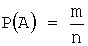

Задача 2. Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет четное число очков, равна…
Воспользуемся формулой 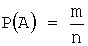
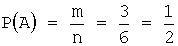
Задача 3. Из урны, в которой находятся 6 черных и 10 белых шаров, вынимают одновременно 2 шара. Тогда вероятность того, что оба шара будут белыми, равна…
Воспользуемся формулой 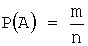
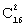
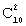
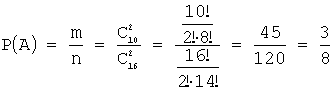
Задача 4. Два предприятия производят разнотипную продукцию. Вероятности их банкротства в течение года равны 0,1 и 0,2 соответственно. Тогда вероятность того, что в течение года обанкротится хотя бы одно предприятие, равна…
Введем обозначения событий: A 1 — обанкротится первое предприятие; A 2 — обанкротится второе предприятие; A — обанкротится хотя бы одно предприятие; 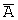
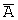
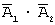
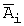
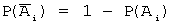
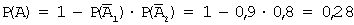
Задача 5. Два стрелка производят по одному выстрелу. Вероятность попадания в цель для первого и второго стрелков равны 0,7 и 0,85 соответственно. Тогда вероятность того, что в цель попадет только один стрелок, равна …
Введем обозначения событий: A 1 — в цель попадет первый стрелок, A 2 — в цель попадет второй стрелок, A — в цель попадет только один стрелок. Тогда 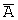
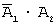
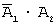
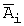
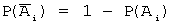

Задача 6. Устройство состоит из трех элементов, работающих независимо. Вероятности безотказной работы этих элементов (в течение рабочего дня) равны соответственно 0,9, 0,8 и 0,7. Тогда вероятность того, что в течение рабочего дня будут работать безотказно все три элемента, равна…
Введем обозначения событий: Ai — в течение рабочего дня безотказно работает i — ый элемент, A – в течение рабочего дня работают безотказно все три элемента. Тогда A = A 1 · A 2 · A 3 . Так как, по условию задачи, события A 1 , A 2 и A 3 независимы, то P ( A )= P ( A 1 · A 2 · A 3 )=
Задача 7. В первой урне 3 черных и 7 белых шаров. Во второй урне 4 белых и 6 черных шаров. В третьей урне 11 белых и 9 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна…
Для вычисления вероятности события A (вынутый наудачу шар – белый) применим формулу полной вероятности: 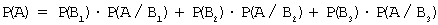
Здесь: 
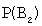
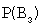
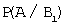

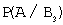
Тогда 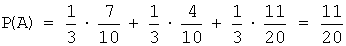
Задача 8. В первой урне 6 черных и 4 белых шара. Во второй урне 2 белых и 18 черных шаров. Из наудачу взятой урны вынули один шар, который оказался белым. Тогда вероятность того, что этот шар извлечен из первой урны, равна…
Предварительно вычислим вероятность события A (вынутый наудачу шар – белый) по формуле полной вероятности: 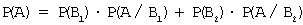
Здесь: 
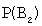
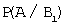

Тогда 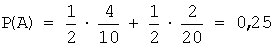
Теперь вычислим условную вероятность того, что шар извлечен из первой урны, если он оказался белым, по формуле Байеса:
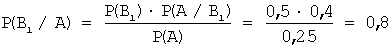
Задача 9. С первого станка на сборку поступает 45%, со второго – 55% всех деталей. Среди деталей первого станка 90% стандартных, второго – 80%. Тогда вероятность того, что взятая наудачу деталь окажется нестандартной, равна …
Для вычисления вероятности события A (взятая наудачу деталь окажется нестандартной) применим формулу полной вероятности: 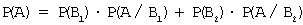

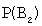
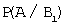
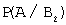
Тогда
P ( A )=0,45(1-0,9)+0,55(1-0,8)=0,045+0,11=0,155.
Задача 10. С первого станка на сборку поступает 20%, со второго – 80% всех деталей. Среди деталей первого станка 90% стандартных, второго – 70%. Взятая наудачу деталь оказалась стандартной. Тогда вероятность того, что эта деталь изготовлена на первом станке, равна …
Предварительно вычислим вероятности события A (взятая наудачу деталь окажется стандартной) по формуле полной вероятности: 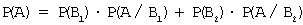
Здесь: 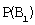
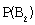
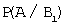

Тогда 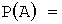
Теперь вычислим условную вероятность того, что деталь изготовлена на первом станке, если она оказалась стандартной, по формуле Байеса:
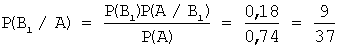
Задача 11. Дискретная случайная величина задана законом распределения вероятностей
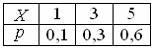
Тогда ее функция распределения вероятностей имеет вид…
По определению F ( x )= P ( X x ).
Тогда
а) при 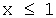
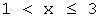
в) при 
F ( x )= P ( X =1)+ P ( X =3)=0,1+0,3=0,4,
г) при x > 5,
F(x)=P(X=1)+ P(X=3)+P(X=5)+P(X=6)= 0,1+0,3+0,6=1.
Следовательно,
Задача 12. Дискретная случайная величина задана законом распределения вероятностей

Тогда значения a и b могут быть равны…
Так как сумма вероятностей возможных значений равна 1, то a + b =1-0,1-0,2=0,7. Этому условию удовлетворяет ответ: a =0,4, b =0,3.
Задача 13. Даны две независимые дискретные случайные величины X и Y :
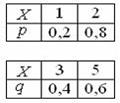
Тогда закон распределения вероятностей суммы X + Y имеет вид…
Возможные значения xij суммы дискретных случайных величин X + Y определяются как xij = xi + yj , а соответствующие вероятности как произведение pij = pi ∙ qj = P ( X = xi )∙ P ( Y = yj ).
Тогда ответ:
Задача 14. Проводится n независимых испытаний, в каждом из которых вероятность появления события A постоянна и равна 0,2. Тогда математическое ожидание дискретной случайной величины X — числа появлений события A в n =100 проведенных испытаниях, равно…
Случайная величина X подчиняется биномиальному закону распределения вероятностей. Поэтому M ( X )= np =100∙0,2=20.
Задача 15. Непрерывная случайная величина задана функцией распределения вероятностей:
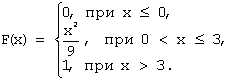
Тогда плотность распределения вероятностей имеет вид…
Плотность распределения вероятностей непрерывной случайной величины вычисляется по формуле: f ( x )= F ’( x ). Тогда 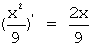
Задача 16. Непрерывная случайная величина X задана плотностью распределения вероятностей 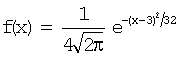
Плотность распределения вероятностей нормально распределенной случайной величины имеет вид: 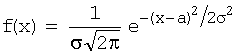
Задача 17. Дискретная случайная величина задана законом распределения вероятностей
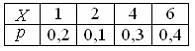
Тогда ее функция распределения вероятностей имеет вид…
По определению F ( x )= P ( X x ).
Тогда
а) при 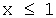
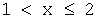
в) при 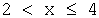
F ( x )= P ( X =1)+ P ( X =2)=0,2+0,1=0,3,
г) при 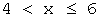
F ( x )= P ( X =1)+ P ( X =2)+ P ( X =4)=0,2+0,1+0,3=0,6,
д) при x > 6,
F(x)=P(X=1)+ P(X=2)+P(X=4)+P(X=6)=1.
Следовательно,
Задача 18. Даны две независимые дискретные случайные величины X и Y :
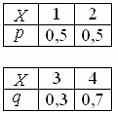
Решение.
Тогда закон распределения вероятностей суммы X + Y имеет вид…
Возможные значения xij суммы дискретных случайных величин X + Y определяются как xij = xi + yj , а соответствующие вероятности как произведение pij = pi ∙ qj = P ( X = xi )∙ P ( Y = yj ).
Тогда правильным будет ответ:

Задача 19. Основная гипотеза имеет вид H 0 : σ 2 =4. Тогда конкурирующей может являться гипотеза…
Конкурирующей (альтернативной) называют гипотезу, которая противоречит основной гипотезе. Условию σ 2 =4 противоречит H 1 :σ 2 >4.
Задача 20. При построении выборочного уравнения парной регрессии вычислены: выборочный коэффициент корреляции r В =0,85 и выборочные средние квадратические отклонения σ X =3,2 σ Y =1,6. Тогда выборочный коэффициент регрессии X на Y равен…
Выборочный коэффициент регрессии X на Y вычисляется по формуле: 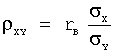
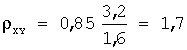
Задача 21. Выборочное уравнение парной регрессии имеет вид y =-1,56-2,3 x .
Тогда выборочный коэффициент корреляции может быть равен…
(Варианты ответа: |1,56 | — 0,87 | — 2,3 | 0,87)
Значение выборочного коэффициента корреляции, во-первых, принадлежит промежутку [-1,1], а во-вторых, его знак совпадает со знаком выборочного коэффициента регрессии. Этим условиям удовлетворяет значение -0,87.
Задача 22. Выборочное уравнение парной регрессии имеет вид y =6-3 x . Тогда выборочный коэффициент корреляции может быть равен…
( Варианты ответов: 0,9 | -3,0 | 6,0 | — 0,9 )
Значение выборочного коэффициента корреляции, во-первых, принадлежит промежутку [-1,1], а во-вторых, его знак совпадает со знаком выборочного коэффициента регрессии. Этим условиям удовлетворяет значение -0,9 .
Задача 23. Выборочное уравнение парной регрессии имеет вид y =-5+2 x . Тогда выборочный коэффициент регрессии равен…
Если выборочное уравнение парной регрессии имеет вид y =α+β x , то выборочный коэффициент регрессии равен β. То есть β=2.
Задача 24. При построении выборочного уравнения парной регрессии вычислены: выборочный коэффициент корреляции r В =0,75 и выборочные средние квадратические отклонения σ X =1,1 σ Y =2,2. Тогда выборочный коэффициент регрессии X на Y равен…
Выборочный коэффициент регрессии X на Y вычисляется по формуле: 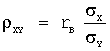
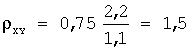
Задача 25. Мода вариационного ряда 1,2,2,3,3,3,4 равна…
Модой вариационного ряда называется варианта, имеющая наибольшую частоту. Такой вариантой является варианта 3, частота которой равна
Задача 26. Медиана вариационного ряда 3,4,5,6,7,12 равна…
Медианой вариационного ряда называется варианта, расположенная в середине вариационного ряда. Так как в середине ряда располагаются две варианты: 5 и 6, то медиана равна их средней арифметической 5,5.
Задача 27. Размах варьирования вариационного ряда 3,5,5,7,9,10,16 равен…
Размах варьирования вариационного ряда определяется как R = xmax — xmin , то есть R =16-3=13.
Задача 28. В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 8, 10, 12. Тогда несмещенная оценка дисперсии равна…
Несмещенная оценка дисперсии вычисляется по формуле: 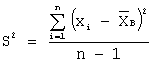
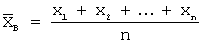
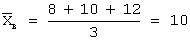

Задача 29. Из генеральной совокупности извлечена выборка объема n =20:
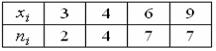
Тогда несмещенная оценка математического ожидания равна…
Несмещенная оценка математического ожидания вычисляется по формуле: 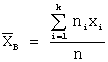
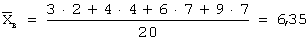
Задача 30. Проведено пять измерений (без систематических ошибок) некоторой случайной величины (в мм): 9, 10, 11, 13, 14. Тогда несмещенная оценка математического ожидания равна…
Несмещенная оценка математического ожидания вычисляется по формуле: 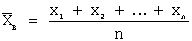

Задача 31. Дана интервальная оценка (8,45;9,15) математического ожидания нормально распределенного количественного признака. Тогда точечная оценка математического ожидания равна…
Интервальная оценка математического ожидания нормально распределенного количественного признака представляет собой интервал, симметричный относительно точечной оценки. Тогда точечная оценка будет равна 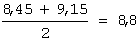
Задача 32. Дана интервальная оценка (10,45;11,55) математического ожидания нормально распределенного количественного признака. Тогда точность этой оценки равна…
Точность интервальной оценки ( a ; b ) определяется как 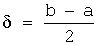
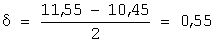
Задача 33. Из генеральной совокупности извлечена выборка объема n =50, гистограмма частот которой имеет вид:
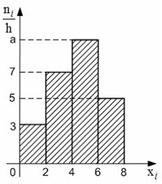
Тогда значение a равно…
Так как объем выборки вычисляется как n =( a +7+5+3) h , то a =50/2-7-5-3=10.
Видео:Метод наименьших квадратов. Парная регрессия расчет без Excel @economc #МНК #регрессия #корреляцияСкачать

Элементы корреляционного и дисперсионного анализа.
Если все варианты увеличить на 3, то коэффициент корреляции…
— уменьшиться на 3
— увеличится в 3 раза
— увеличится в 9 раз
— уменьшиться на 9
Если все варианты увеличить на 5, то коэффициент корреляции…
— уменьшиться на 5
— увеличится в 5 раза
— увеличится в 25 раз
— уменьшиться на 25
Если все варианты увеличить на 4, то коэффициент корреляции…
— уменьшиться на 4
— увеличится в 4 раза
— увеличится в 16 раз
— уменьшиться на 16
Внутригрупповая дисперсия вычисляется по формуле…
—
+
—
—
Межгрупповая дисперсия вычисляется по формуле…
—
—
+
—
Общая дисперсия вычисляется по формуле…
+
—
—
—
Выборочное уравнение парной регрессии имеет вид у= -3,2+1,6 х. Тогда выборочный коэффициент регрессии равен …
Выборочное уравнение парной регрессии имеет вид у= -4,3+0,4х. Тогда выборочный коэффициент регрессии равен …
Выборочное уравнение парной регрессии имеет вид у=2,8+1,3х. Тогда выборочный коэффициент регрессии равен …
Выборочное уравнение парной регрессии имеет вид у= -2,6+1,3х. Тогда выборочный коэффициент корреляции может быть равен …
Выборочное уравнение парной регрессии имеет вид у= 2,5+1,25х. Тогда выборочный коэффициент корреляции может быть равен …
Выборочное уравнение парной регрессии имеет вид у= 6,4-1,6х. Тогда выборочный коэффициент корреляции может быть равен …
Выборочное уравнение парной регрессии имеет вид у=2,8+0,8х, средние квадратические отклонения 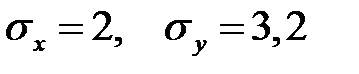
Выборочное уравнение парной регрессии имеет вид у=3,6+0,6х, средние квадратические отклонения 
Выборочное уравнение парной регрессии имеет вид у= -1,48+3,9х, средние квадратические отклонения 
При построении выборочного уравнения парной регрессии вычислен выборочный коэффициент корреляции 

При построении выборочного уравнения парной регрессии вычислен выборочный коэффициент корреляции 
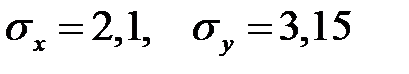
При построении выборочного уравнения парной регрессии вычислен выборочный коэффициент корреляции 

Элементы комбинаторики
Количество перестановок из букв слова «корсаж», в которых буква «к» на первом месте, а буква «ж» — в конце слова, равно …
Количество перестановок из букв слова «лидер», в которых буква «е» на первом месте, а буква «д» — в конце слова, равно …
Количество перестановок из букв слова «планета», в которых буква «е» на первом месте, а буква «п» — в конце слова, равно …
Количество перестановок букв слова «бином» равно …
Количество перестановок букв слова «угол» равно …
Количество перестановок букв слова «граф» равно …
В коробке 6 цветных карандашей. Число способов выбрать два из них равно …
Число способов выбрать из группы в 20 студентов двух дежурных равно …
Число способов выбрать из группы в 20 студентов старосту и заместителя равно …
Из ящика, где находится 13 деталей, пронумерованных от 1 до 13, требуется вынуть 5 деталей. Тогда количество всевозможных комбинаций номеров вынутых деталей равно …
—
+
В цветочном киоске 7 видов цветов. Количество способов выбора 3 цветов различно вида равно …
+
—
На собрании членов кооператива присутствуют 20 человек. Тогда количество комбинаций выбора председателя правления, его заместителя и бухгалтера равно …
—
+
—
Соединения, из которых каждое содержит m элементов, взятых из числа данных n элементов, которые отличаются друг от друга, либо самими элементами, либо порядком их расположения.
Соединения, из которых каждое содержит m элементов, взятых из числа данных n элементов, которые отличаются друг от друга, по крайней мере, одним элементом.
Соединения, из которых каждое содержит все n элементов и которые отличаются друг от друга лишь порядком расположения элементов.
Количество перестановок слова «свитер», в которых буква «с» на первом месте равно
Сколькими способами можно с помощью букв M, N, R, F, S обозначить вершины пятиугольника.
Сколькими способами можно сформировать команду из 4 студентов для участия в командной олимпиаде из 10 претендентов.
Сколько трехзначных чисел можно составить из множества цифр , если все цифры в нем различные.
Количество перестановок в слове «книга» равно…
На занятии по математике преподаватель разбивает группу студентов по 4 человек. Сколько групп может быть образовано в группе из 24 студентов?
Сколько существует семизначных чисел, состоящих из цифр 4, 5 и 6, в котором цифра 4 повторяется 3 раза, а цифры 5 и 6 – по 2 раза?
Сколькими способами можно сформировать команду из 4 человек для участия в спортивных соревнованиях из 8 претендентов.
Если «словом» считать любую комбинацию букв, то число «слов», полученных перестановкой букв в слове «РАМА», равно…
Видео:Нелинейная регрессия в MS Excel. Как подобрать уравнение регрессии? Некорректное значение R^2Скачать

11.3.2. Выборочное уравнение парной линейной регрессии
Рассмотрим МНК в случае нахождения выборочного уравнения парной линейной регрессии.
Пусть имеются результаты наблюдений 
Найдя частные производные по а и b и приравняв их к нулю, получим систему
откуда нетрудно получить 
Таким образом, получили выборочное уравнение парной линейной регрессии Y на X
Замечание 11.10. Выборочный коэффициент регрессии обозначается следующим образом:
При построении выборочного уравнения линейной регрессии полученные оценки а и b являются СВ. При этом возможные значения оценок рассеиваются вокруг истинных значений параметров. Чтобы определить меру рассеивания, вычисляют средние квадратические ошибки коэффициентов а и Ь:
Стандартная ошибка параметров регрессии используется для оценки качества подбора функции регрессии.
Пример 11.7. Компания «Орион» располагает системой гипермаркетов в различных регионах России. Для оценки эффективности рекламы были собраны данные по 12 случайно выбранным областям. В каждой области сравнивались собственные затраты на рекламу и объем продаж предыдущего года с аналогичными показателями основного конкурента. Фиксировались две переменные: X — затраты компании на рекламу как процент от аналогичных затрат конкурента; Y — объем продаж компании как процент от объемов продаж конкурента. Результаты представлены в таблице:
📺 Видео
Математика #1 | Корреляция и регрессияСкачать

Интерпретация коэффициента при логарифмировании в уравнениях регрессииСкачать

МЕТРИКИ РЕГРЕССИИ В МАШИННОМ ОБУЧЕНИИ | MAE, MSE, RMSE, R2, коэффициент детерминации.Скачать

Парная регрессия: линейная зависимостьСкачать

Линейная регрессияСкачать

Как вычислить линейный коэффициент корреляции в MS Excel и построить уравнение регрессии?Скачать

Эконометрика Линейная регрессия и корреляцияСкачать

Парная нелинейная регрессияСкачать

Метод наименьших квадратов. Линейная аппроксимацияСкачать

Нелинейная регрессияСкачать

РегрессияСкачать

Что такое регрессия и какие виды регрессии имеются? Душкин объяснитСкачать

МНК. Пример 2. Парная регрессияСкачать

Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать

Как вычислить линейный коэффициент корреляции по таблице? Корреляционное поле и прямая регрессииСкачать

Эконометрика. Множественная регрессия и корреляция.Скачать

Что такое линейная регрессия? Душкин объяснитСкачать

Эконометрика. Линейная парная регрессияСкачать