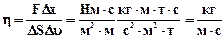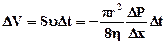Вязкость истинных и коллоидных растворов уравнение ньютона и пуазейля (4 видео)

Содержание

Вязкость жидкости. Уравнение Ньютона. Закон Пуазейля
Лако-красочные материалы — производство
Технологии и оборудование для изготовления красок, ЛКМ
Вязкость ИСТИННЫХ И КОЛЛОИДНЫХ РАСТВОРОВ
Реологические свойства дисперсных систем
Реологические свойства коллоидных систем. Ньютоновские жидкости
📹 Видео

Видео:Вязкость и течение Пуазёйля (видео 14) | Жидкости | ФизикаСкачать

Вязкость жидкости. Уравнение Ньютона. Закон Пуазейля

Реальная жидкость и реальный газ обладают вязкостью (внутренним трением).

При течении реальной жидкости отдельные ее слои воздействуют друг на друга с силами касательными к слоям. Это явление и называют внутреннем трением или вязкостью.

Сила внутреннего терния выражается уравнением Ньютона:

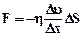
где η – вязкость жидкости, ∆υ/∆х – градиент скорости, ∆S – площадь соприкосновения слоев.

Единицей измерения вязкости является

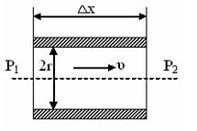
Течение вязкой жидкости по трубам представляет для медицины особый интерес, так как кровеносная система состоит в основном из цилиндрических сосудов разного диаметра.

Пуазейль установил, что скорость жидкости при ламинарном движении по трубе круглого сечения пропорциональна градиенту давления, квадрату радиуса трубы и обратно пропорциональна вязкости

или

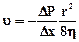
Дата добавления: 2015-06-22 ; просмотров: 2270 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Коллоидные растворы. Дисперсные системыСкачать

Лако-красочные материалы — производство

Видео:Вязкость. Ламинарное и турбулентное течения жидкостей. 10 класс.Скачать

Технологии и оборудование для изготовления красок, ЛКМ

Видео:Дисперсные системы (образование, свойства и устойчивость коллоидных растворов)Скачать

Вязкость ИСТИННЫХ И КОЛЛОИДНЫХ РАСТВОРОВ

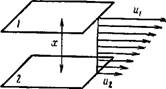
Для того чтобы лучше понять особенности вязкости коллоидных систем, напомним основные понятия о вязкости и механизме течения обычных ннзкомоле — кулярных жидкостей, таких, как вода, спирт, бензол и т. д Представим себе, как это показано на рнс. X. 3, что с помощью приложенной внешней снлы мы привели в не слишком быстрое движение тонкий слой жидкости в направлении, параллельном плоскости поверхности ЖИДКОСТИ, СО скоростью «1. Опыт показывает, что нижележащие слон ие останутся в покое, а тоже прндут в движение. Верхний слой благодаря внутреннему трению, возникающему между слоями и являющемуся следствием хаотического теплового движения молекул и межмолекулярных снл притяжения, увлекает нижележащие слон, причем скорость движения этих слоев уменьшается от верхнего к нижнему, так как нижние слон тормозят движение вышележащих. Уменьшение этой скорости прямо пропорционально расстоянию х от верхнего слоя до нижнего. Существенно, что такое движение слоев жидкости, называемое ламинарным течением, может быть вызвано сколь угодно малой силой, но действующей достаточно длительное время. Внутреннее трение, как и внешнее, является, конечно, причиной днсснпацни (рассеяния) энергии, т. е. необратимого превращения ее в тепло.

По определению вязкости, данному Ньютоном, снла внутреннего трения F, Равная по значению, но обратная по направлению приложенной извне силе, пропорциональна площадн слоя S, к которому приложена эта снла, и градиенту скорости движения Du/Dx между слоями.

Где т| — коэффициент пропорциональности, называемый коэффициентом вязкости (илн вязкостью), зависящей от природы жидкости.

Относя снлу F к площадн сдвига, уравнение (X. 1) можно переписать в виде:

Рнс. X, 3. Распределение скоростей движения жидкости между двумя параллельно движущимися слоями (/ и 2), находящимися на расстоянии х.

Где Р — напряжение сдвига, поддерживающее течение жидкости.

Из уравнения (X, 1) можно видеть, что единицами измерения вязкости являются г/(см-с),

В честь французского ученого Пуазейля, впервые изучившего движение жидкостей в капиллярах, единица вязкости названа пуазом (П); 1 пуаз соответствует вязкости жидкости, при которой для поддержания градиента скорости в 1 см/с нужна сила в 1 дин на 1 см2.

Для сравнительно маловязких жидкостей обычно пользуются величиной в сто раз меньшей — сантипуазом (сП). Следует помнить, что вязкость воды при 20 °С весьма близка к 1 сП.

Вычисленная из уравнения Ньютона вязкость в условиях ламинарного течения жидкости не зависит ни от способа измерения, ни от типа и размеров примененного вискозиметра, т. е. является инвариантной характеристикой данной жидкости.

Величина 1/т|, обратная вязкости, называется текучестью. Она характеризует подвижность жидкости под влиянием внешних воздействий.

Ламинарное течение жидкости по трубкам описывается известным уравнением Пуазейля [26]:

Где V — объемная скороеть истечения; г и / — радиус и длина трубки; р — разность давлений на концах трубки; ті —вязкость жидкости.

Это уравнение найдено Пуазейлем в 1842 г эмпирическим путем

Уравнение Ньютона, а следовательно, и уравнение Паузейля соблюдаются, если жидкость движется ламинарно, т. е. в виде слоев, имеющих различную скорость и не смешивающихся друг с другом. Такой режим наблюдается лишь при сравнительно малых скоростях течения. При больших скоростях ламинарный характер течения переходит в турбулентный, характеризующийся возникновением в движущейся жидкости завихрений. Если применять к такому течению уравнения Ньютона и Пуазейля, то коэффициент вязкости теряет свой обычный смысл, так как его значение при турбулентном течении зависит не только от природы жидкости, но становится функцией скорости движения жидкости. Очевидно, в этом случае можно говорить лишь об эффективной или кажущейся вязкости, понимая под ней условную величину, вычисленную для данной скорости течения по уравнениям Ньютона или Пуазейля.

Рейнольде в 1883 г. показал, что при течении жидкости по трубке с гладкими стенками ламинарное движение переходит в турбулентное, когда число Рейнольдса Re превысит известное значение. Число или критерий Рейнольдса представляет собой безразмерное отношение:

Где р — плотность жидкости.

Как видно из свотношения (X, 4), ламинарное движение переходит в турбулентное при тем меньших скоростях, чем больше радиус трубки и плотность жидкости и чем меньше ее вязкость. Наличие «в жидкости взвешенных частиц, особенно неправильной формы, способствует так называемой ранней турбулентности, т. е. тому, что ламинарное течение переходит в турбулентное при значительно меньших значениях Re.

Уравнения Ньютона или Пуазейля количественно описывают течение жидкости, но ничего не говорят о сущности явления. Весьма важно для понимания процесса течения жидкости разобраться в его молекулярном механизме.

Механизм течения жидкости можно представить себе правильно только исходя из современных представлений о строении жидкости, развитых Я. И. Френкелем, а также Эйрингом (см. гл. III).

Как известно, молекулы всякой жидкости находятся в непрерывном тепловом движении, передвигаясь относительно друг-друга путем последовательного перемещения в дырки, имеющиеся в жидкости. Пока на жидкость не действуют
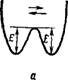
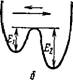
какие-нибудь внешние силы, перемещении равновероятны во всех направлениях. В этом случае зависимость потенциальной энергии от положения молекул вблизи дырки можно охарактеризовать схемой а иа рис. X, 4. Однако если жидкость находится под действием внешнего силового поля, которое стремится сместить молекулы в определенном направлении, то потенциальная энергия после перехода молекул в новое положение Ез будет меньше потенциальной энергии до перехода Еі. При этом потенциальная яма деформируется и примет вид, показанный на схеме б рис. X, 4. Поскольку скачки молекул, приводящие к уменьшению потенциальной энергии, происходят чаще, чем обратные, хаотическое движение приобретает направленность и наблюдается перенос вещества, т. е. течение жидкости.»

Совершенно очевидно, что частота перемещения молекул в жидкости тем больше, чем выше средняя кинетическая энергия теплового движения молекулы KT, и тем меньше, чем бблыпую работу надо затратить для того, чтобы молекула могла совершить скачок. Следовательно, с повышением температуры промежуток времени между перемещениями молекул в соседние равновесные положения становится все короче и короче, а жидкость при одном и том же напряжении сдвига будет все более и более подвижной. Кроме того, при повышении температуры и увеличении энергии теплового движения все большее число молекул обладает энергией, необходимой для совершения скачка. Наконец, с повышением температуры происходит термическое расширение жидкости, что приводит к возрастанию числа дырок и к увеличению их размера. Все это обусловливает значительное снижение внутреннего треиия илн повышение текучести. Так, вязкость воды при изменении температуры на 1 °С в интервале не слишком высоких температур изменяется на 2—3%.

Текучесть и вязкость, как это следует из молекулярной модели вязкого течения, изменяются с температурой приблизительно по экспоненциальному закону:

Где А и А’ — коэффициенты, сравнительно мало • зависящие от температуры; Е — энергия активации, которую должна приобрести молекула, чтобы перескочить в новое положение равновесия; K — постоянная Больцмана; Т—абсолютная температура.

При известной температурной зависимости текучести или вязкости, логарифмируя эти уравнения, легко найти значение энергии активации, поскольку связь между In ц и 1/7″ должна выражаться прямой линией. Однако следует помнить, что эта графическая зависимость для разных жидкостей представляет собой прямую только в относительно узкой области температур; в более широком температурном интервале обычно наблюдается отклонение от прямолинейности.

Опыт показывает, что энергия активации вязкого течения жидкости обычно равна нескольким килокалориям на моль.

Определение вязкости жидкостей

Вязкость жидкостей можно определять с помощью различных методов. Остановимся кратко лишь на важнейших из них.

Рис. X, 4. Зависимость потенциальной энергии молекулы от ее положения

Вблизи дырки: а—в отсутствие внешнего силового поля; б — прн действии внешнего силового ПОЛЯ.

Метод падающего шарика сводится к определению скорости свободного падения в жидкости шарика известного объема и массы. Для того чтобы не возникало турбулентного движения жидкости, скорость падения шарика должна
быть не слишком большой, а сосуд, в котором падает шарик, достаточно широким. Коэффициент вязкости вычисляют по уравнению, которое легко выводите® из уравнения (111,39):

Ті = 2г2 (р — ро) g/(9u) (Х,7>

Нетрудно видеть, что, определяя вязкость по скорости падения шарика,, экспериментатор решает задачу, обратную той, которую ему приходится решать при нахождении радиуса частицы суспензии по скорости оседания.

Из уравнения (X, 7) следует, что скорость падения шарика обратно пропорциональна вязкости жидкости. Подобная зависимость соблюдается и тогда,, когда шарик падает не в широком сосуде, а движется в наклонной стеклянной трубке, заполненной жидкостью, так, как это происходит в известном вискозиметре Гепплера.

Метод истечения жидкости через капилляр основан на измерении времен» вытекания определенного объема жидкости через капилляр^ радиус и длина которого известны. В этом случае вязкость вычисляют по уравнению:

Где V— объем жидкости, вытекшей за время т; остальные обозначения те же,, что и в уравнении (X, 3).

Определение с помощью ротационных вискозиметров. Приборы, применяемые для определения вязкости по этому методу, представляют собой два коаксиальных цилиндра. В кольцевой зазор между цилиндрами заливают исследуемую жидкость. Один из цилиндров (обычно внутренний) приводят во вращение, например, с помощью груза, блока и шнура. После весьма краткого периода устанавливается стационарный режим течения жидкости между цилиндрами. Вязкость находят, определяя число оборотов вращающегося цилиндра в единицу времени. Ряд конструкций прибора такого типа в Советском Союзе разработай М. П. Воларовичем.

Другая разновидность ротационного прибора, предложенная еще Ф. Н. Шведовым в прошлом столетии, представляет собой также два коаксиальных цилиндра, из которых внешний приводится во вращение с постоянной скоростыо с помощью электромотора, а внутренний подвешен на тонкой упругой нити иь снабжен указателем для отсчитывйния угла закручивания. Жидкость заливают в пространство между цилиндрами. Внешний цилиндр при вращении увлекает за собой жидкость, которая в свою очередь приводит во вращение внутренний: цилиндр и закручивает его на некоторый угол до тех пор, пока момент силы кручения ие станет равным моменту сил трения. Так как нить, на которой подвешен внутренний цилиндр, упруга, то этот угол всегда пропорционален вязкости.

По уравнению, связывающему скорость вращения и угол закручивания цилиндра, зная константы прибора, можно вычислить вязкость.

Очень часто на практике применяют не абсолютные, а относительные методы определения вязкости, что позволяет исключить из расчета константы приборов — При этом измеряют время падения шарика, время истечения или другие параметры для стандартной жидкости, а затем определяют ту же величину и для исследуемой жидкости. Поскольку значения вязкости пропорциональны измеренным величинам, то, зная вязкость стандартной жидкости, можно по полученным результатам вычислить вязкость исследуемой жидкости. Так как вязкость сильно зависит от температуры, ее следует измерять всегда при постоянной темнера- туре, термостатнруя прибор.

Более подробно методы определения вязкости рассматриваются в руководствах к лабораторным занятиям по коллоидной химии.

Отлйчие течения золей от течения обычных индивидуальных: жидкостей или истинных растворов низкомолекулярных вещест» обуславливается тем, что в первых присутствуют во взвешенном состоянии коллоидные частицы, размеры которых значительно превышают размер молекул. «Наличие таких частиц изменяет пути -отдельных молекул текущей жидкости и способствует перемешиванию отдельных слоев. Именно в результате этого у дисперсных систем наблюдается ранняя турбулентность, т. е. переход ламинарного течения в турбулентное при меньших числах Рейнольдса; чем для жидкостей, не содержащих взвешенных частиц. Кроме того, коллоидные частицы сужают пространство, занятое самой жидкостью в потоке, и увеличивают таким образом средний градиент скорости в направлении, перпендикулярном течению жидкости. Вследствие этого вязкость золя всегда несколько выше вязкости дисперсионной’ средыг

Наконец, характерной особенностью многих золей является неподчинение их зависимостям, выражаемым уравнениями Ньютона я Пуазейля. Для обычных жидкостей объем жидкости, протекшей через капилляр в единицу времени, прямо пропорционален разности давлений р на концах капилляра. Точно так же для обычных жидкостей наблюдается прямая зависимость между углом поворота внутреннего цилиндра и скоростью вращения наружного цилиндра в ротационном приборе типа вискозиметра Ф. Н. Шведова. Для многих же золей, эмульсий и растворов высокомолекулярных веществ такая зависимость отсутствует, а вычисленная по соответствующему уравнению вязкость имеет переменное значение и является функцией градиента скорости. Иными словами, вязкость многих дисперсных систем не являемся инвариантной характеристикой системы, а зависит от условии ее определения, например от скорости течения жидкости в вискозиметре, от типа и размеров прибора.

Законам Ньютона и Пуазейля не подчиняются коллоидные системы с удлиненными частицами и частицами, способными деформироваться, а также структурированные коллоидные системы. Причина аномалии вязкого течения коллоидных систем с вытянутыми, палочкообразными частицами заключается в том, что по мере увеличения напряжения сдвига,.обусловливающего течение, такие частицы ориентируются своей длинной осью в направлении потока, в результате чего понижается гидродинамическое сопротивление и этим самым убыстряется движение жидкости. Ориентацию вытянутых частиц в направлении потока легко доказать, измеряя двойное лучепреломление в золе при все возрастающем градиенте скорости. _

У систем с деформирующимися частицами, например у эмульсий, наблюдается аналогичная зависимость. Капельки дисперсной фазы с возрастанием приложенного напряжения сдвига и увеличением скорости течения удлиняются, превращаясь из шариков в эллипсоиды, что, конечно, облегчает течение и понижает вязкость. То же самое наблюдается и при течении растворов высокомолекулярных соединений с гибкими, свернутыми в клубок макромолекулами. Здесь падение вязкости обусловлено распрямлением молекул и их ориентацией в направлении потока. Конечно, во всех перечисленных случаях речь идет о кажущейся или эффективной вязкости г)*, так как истинная вязкость жидкости от скорости течения зависеть не может.

Законам Ньютона и Пуазейля не подчиняются также структурированные жидкости. В связи с большим практическим значением и некоторыми принципиальными особенностями вязкость структурированных жидкостей целесообразно рассмотреть отдельно.

В заключение отметим, что все жидкости, подчиняющиеся закону Ньютона, называются нормальными; системы же, способные течь, но не подчиняющиеся уравнению Ньютона, принято называть Аномальными. При работе с капиллярным вискозиметром можно воспользоваться весьма простым приемом для того, чтобы судить, является ли исследуемая жидкость нормальной или аномальной. Для этого избыточное давление р, под действием которого истекает жидкость, умножают на соответствующее время истечения определенного объема жидкости. Так как уравнение Пуазейля можно представить в виде:

То совершенно очевидно, если произведение рх не зависит от давления, под которым происходило истечение, то жидкость является нормальной, если же зависит, то она аномальна. При работе с ротационным вискозиметром таким же критерием может служить независимость произведения числа оборотов цилиндра в единицу времени на величину груза, обеспечивающего вращение цилиндра.

Видео:Суспензии, коллоиды и растворыСкачать

Реологические свойства дисперсных систем

Проявление молекулярно-кинетических свойств коллоидных систем неразрывно связано с их реологическими (вязкостными) свойствами.

Реология — это наука о деформации и течении материалов. К реологическим свойствам относят вязкость и текучесть.

Видео:Урок 137. Движение тела в жидкости и газе.Скачать

Реологические свойства коллоидных систем. Ньютоновские жидкости

Реологические свойства. Все многообразие коллоидных систем можно разделить на свободно — и связнодисперсные. Отсутствие или различная степень структурирования значительным образом сказывается на их структурно-механических (реологических) свойствах — упругости, прочности, вязкости (текучести) и пластичности. Реологические свойства системы зависят от ее природы и физического состояния и проявляются по-разному в жидком, твердом и промежуточном (переходном) состояниях.

Реология — это наука о деформации и течении материалов. В коллоидной химии методами реологии пользуются для изучения структуры и вязко-текучих свойств дисперсных систем.

Деформация — смещение точек системы, при котором не нарушается ее сплошность (тело не разрушается). Упругая деформация, характерная для твердых тел, обратима. Она полностью исчезает практически сразу после снятия нагрузки. Остаточная деформация необратима, изменения в системе остаются и после снятия нагрузки. Остаточная деформация свойственная пластичным системам. Следует отметить, что пластичность может наблюдаться, начиная с некоторой нагрузки, называемой пределом текучести Р_пред (при малых нагрузках система может проявлять упругие свойства), после которой устанавливается течение с постоянной скоростью.

Вязкие тела отличаются от пластичных тем, что текут при любом напряжении. Для них предел текучести равен нулю (Р_пред = 0). Течение — один из видов остаточной деформации, когда величина деформации постоянно увеличивается под действием постоянной нагрузки. Такой вид деформации характерен для жидкостей и газов; в данном разделе будут рассматриваться преимущественно вязко-текучие свойства неструктурированных или слабоструктурированных дисперсных систем.

Вязкостью называют внутреннее трение между слоями данного вещества (жидкости или газа), движущимися относительно друг друга. Текучесть представляет собой свойство, противоположное вязкости.

Реологические свойства вещества зависят от его природы и физического состояния и проявляются по-разному у веществ в жидком, твердом и промежуточном (переходном) состояниях. Вязкость является результатом межмолекулярного взаимодействия, и она тем выше, чем больше силы молекулярного притяжения. Поэтому вязкость полярных веществ всегда больше, чем неполярных, вязкость уменьшается с увеличением температуры.

Если приложить силу к жидкости, она начинает течь. После прекращения действия силы жидкость не возвращается в первоначальное состояние. Следовательно, течение жидкостей приводит к необратимой деформации. Для жидкостей характерны два основных типа течения: ламинарное и турбулентное.

Ламинарным называют течение жидкости в виде параллельных слоев, не перемешивающихся между собой. Примером ламинарно текущей жидкости может служить спокойная равнинная река.

Турбулентное течение — это бурное течение, сопровождающееся образованием завихрений, воронок и взаимным перемешиванием слоев жидкости (подобно горной реке). Рассматриваемые закономерности вязкости будут относиться только к ламинарному режиму течения.

Реальные системы классифицируют по реологическим свойствам на жидкообразные и твердообразные. Отличительной особенностью всех жидкостей является способность к течению при сколь угодно малых давлениях, предел текучести для них равен нулю.

Жидкости, в свою очередь подразделяют на ньютоновские и неньютоновские. К ньютоновским относятся жидкие системы, которые при ламинарном течении подчиняются закону течения Ньютона: напряжение сдвига Р пропорционально градиенту скорости (или скорости развития деформации) — коэффициент вязкости.

Градиент скорости возникает из-за изменения скорости движения жидкости в капилляре в зависимости от расстояния от стенок капилляра. Скорость имеет максимальное значение в центре капилляра, уменьшаясь до нуля за счет сил адгезии в слое, соприкасающемся со стенками капилляра.

Закон Ньютона выражает равновесие между приложенным напряжением Р и силой сопротивления жидкости течению при установившемся равномерном движении. Согласно полученному выражению, коэффициент вязкости (или просто вязкость) равен силе сопротивления (трения) между слоями жидкости при площади соприкасающихся слоев жидкости, равной единице, и градиенте скорости течения между слоями, равном единице.

Единицей вязкости в СИ является или Па с.

Для ньютоновских или нормально вязких жидкостей вязкость не зависит ни от приложенного давления, ни от градиента скорости (в условиях равномерного ламинарного течения): . Графически зависимость вязкости от давления (напряжения сдвига) имеет вид горизонтальной прямой в области ламинарного течения.

На основе экспериментальных данных по измерению скорости вытекания жидкостей из капилляров Ф. Пуазейль получил для ньютоновских жидкостей эмпирическое уравнение, согласно которому объем V жидкости, вытекающей из капилляра, прямо пропорционален давлению Р, под которым жидкость продавливается через капилляр, времени наблюдения t и обратно пропорционален вязкости (константа К, зависит от длины l и радиуса г капилляра):

Зависимость вязкости от концентрации дисперсной фазы для таких систем описывается уравнением Эйнштейна: — динамическая вязкость дисперсионной среды; — объемная концентрация дисперсной фазы; — коэффициент, зависящий от формы частиц дисперсной фазы. С увеличением концентрации дисперсной фазы растет взаимодействие между частицами, и обнаруживаются значительные отклонения от уравнения Эйнштейна из-за взаимодействия частиц между собой (структурирования).

Неньютоновские жидкости проявляют аномалии вязкости, т.е. отклонения от законов Ньютона и Пуазейля. Эти жидкости можно еще подразделить на псевдопластические и дилатантные. Для псевдо-пластических жидкостей характерно, что их скорость течения возрастает быстрее, чем приложенное давление. Это говорит об уменьшении коэффициента вязкости при возрастании напряжения. Такие свойства характерны для суспензий с асимметрической формой частиц (палочкообразной) и разбавленных растворов полимеров. При течении систем частицы дисперсной фазы или макромолекулы располагаются по потоку, и сопротивление их движению уменьшается.

Скорость течения дилатантных жидкостей растет медленнее, чем приложенное давление; следовательно, их вязкость увеличивается при повышении давления. Дилатантные системы называют также растекающимися. Многие порошки и уплотненные дисперсные материалы проявляют склонность к растеканию. При малых давлениях (при сдвиге) прежде чем отдельные частицы смогут двигаться относительно друг друга, их взаимная упаковка становится более рыхлой и система увеличивается в объеме. При этом вязкость уменьшается. При возрастании нагрузки частицы вступают в контакт, что приводит к возрастанию вязкости.

Наиболее общим уравнением, описывающим течение неньютоновских жидкостей, является эмпирическое уравнение Оствальда-Вейля: , где k и n — постоянные, характеризующие данную жидкообразную систему. Если n = 1, жидкость является ньютоновской, и константа k совпадает с ньютоновской вязкостью . Таким образом, отклонение n от единицы характеризует степень отклонения свойств неньютоновских жидкостей от свойств ньютоновских жидкостей. При n 1 вязкость растет с увеличением скорости сдвига и напряжения. Соответственно, эти жидкости — дилатантные.

Более сложные реологические кривые характерны для коллоидных систем с большой концентрацией частиц дисперсной фазы. В зависимости от преобладающего типа контактов между частицами дисперсные структуры условно можно разделить на две основные группы: коагуляционные структуры и структуры с фазовыми контактами.

Коагуляционные структуры образуются при потере дисперсной системой агрегативной устойчивости; при достаточном содержании дисперсной фазы обеспечивается армирование всего объема дисперсной системы. Соответствующее содержание коллоидно-дисперсной фазы, способное «отверждать» жидкую дисперсионную среду, может быть очень малым (особенно для резко анизометричных частиц), например, всего лишь 6% по массе для чешуек бентонитовых глин, и менее 0,01% для нитевидных частиц

Характерным свойством коагуляционных структур наряду с относительно невысокой прочностью является их обратимость по отношению к механическим воздействиям, т.е. способность к самопроизвольному восстановлению после механических разрушений (в подвижной дисперсионной среде). Это свойство называют тиксотропией.

Коагуляционные дисперсные структуры образуются пигментами и наполнителями лаков, красок, полимеров. Характерным примером тиксотропных структур являются пространственные сетки, возникающие в дисперсиях глин при их коагуляции под действием электролитов. Тесно с тиксотропией связана реопексия — резкое ускорение восстановления структуры под действием небольшой нагрузки (видимо, при этом облегчается вступление в контакт частиц неправильной формы).

В зависимости от приложенного напряжения сдвига (скорости течения) реологические свойства структурированных дисперсных систем могут меняться от свойств, присущих твердообразным телам, до свойств, характерных для ньютоновских жидкостей. Это разнообразие в реологическом поведении реальной дисперсной системы с коагуляционной структурой описывается полной реологической кривой.

Кривая позволяет выделить четыре характерных участка. При самых малых напряжениях сдвига система может вести себя как твердообразная с высокой вязкостью. Изучение релаксационных свойств коагуляционных структур, возникающих, например, в умеренно концентрированных водных дисперсиях бентонитовых глин, показало, что при малых напряжениях сдвига наблюдается упругая деформация, связанная с взаимной ориентацией анизометричных частиц, способных участвовать в тепловом движении. Высокие значения вязкости обусловлены перетеканием дисперсионной среды из уменьшающихся в размере ячеек в соседние через узкие зазоры и со скольжением частиц относительно друг друга.

При достижении некоторого значения напряжения наступает область медленного вязкопластического течения в системе с почти неразрушенной структурой — область ползучести. На этом участке сдвиг осуществляется за счет флуктуационного процесса разрушения и последующего восстановления коагуляционных контактов, который под действием приложенных извне напряжений приобретает направленность.

В результате броуновского движения частицы, объединенные в единую коагуляционную структуру, испытывают колебания относительно их положения в контактах. Вследствие тепловых флуктуаций некоторые контакты разрушаются, но при этом возникают контакты между частицами в других местах. В среднем число контактов в сформировавшейся структуре остается постоянным во времени и близким к максимальному. При приложении же внешнего поля напряжений разрушение и восстановление контактов приобретают направленность, и наблюдается медленный сдвиг, т.е. ползучесть.

При достижении некоторого напряжения сдвига Рт начинается область энергично разрушаемой структуры пластического течения, вязкость системы резко уменьшается от max до min. После полного разрушения структуры дисперсная система в условиях ламинарного течения проявляет свойства ньютоновской жидкости.

Твердообразные дисперсные структуры с фазовыми контактами (конденсационно-кристаллизационными структурами) образуются в самых разнообразных физико-химических условиях, в том числе при спекании и при прессовании порошков. Дисперсные структуры с фазовыми контактами, возникающие в процессе выделения (конденсации) новой фазы из метастабильных растворов или расплавов, принято называть конденсационными. Если при этом частицы, образующие структуру, имеют ярко выраженный кристаллический характер, то такие структуры называют конденсационно-кристаллизационными или просто кристаллизационными, противопоставил их конденсационным структурам из аморфных новообразований

Твердообразные системы в отличие от жидкостей проявляют признаки течения лишь после приложения некоторого предельного давления. Это означает, что их предел текучести не равен нулю их реологические кривые не проходят через начало координат, а сдвинуты от него на величину предела текучести. Деформации (течение) пластических и псевдопластических твердообразных систем, как и течение жидкостей, необратимы.

Аномалии вязкости могут быть вызваны рядом причин, основными из них являются:

коллоидная дисперсная система реологический

структурообразование — процесс агрегирования частиц коллоидных растворов, суспензий и растворов высокомолекулярных веществ (ВМВ) и образования пространственных легкоразрушаемых структур;

изменение ориентации в потоке частиц удлиненной формы и макромолекул при увеличении градиента скорости;

деформация клубков макромолекул полимера или капель эмульсии в потоке.

Течение твердообразных систем описывается уравнением Бингама:

— пластическая вязкость. Уравнение Бингама является приближенным, так как величина , характеризующая степень структурообразования в системе, является экстраполяционной и не имеет четкого физического смысла. Пластическая вязкость соответствует наименьшей вязкости аномально вязкой системы — псевдопластической жидкости или твердообразного тела на участке кривой, где вязкость не зависит от давления.

Величины и (max — min) характеризуют прочность структуры. На структурирование влияет концентрация и асимметричность частиц дисперсной фазы, температура, время стояния системы.