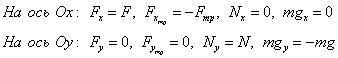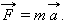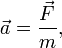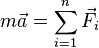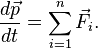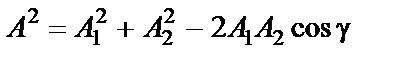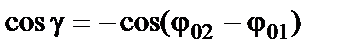Приступая к формулировке второго закона, следует вспомнить, что в динамике вводятся две новые физические величины – масса тела m и сила 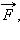
Вторая – сила 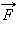
- не зависит от скорости тела
- равна сумме масс всех частиц, из которых состоит это тело
- при любых процессах, происходящих в замкнутой системе тел, ее полная масса остается неизменной.
- величина,
- направление
- точка приложения.
В качестве примера рассмотрим данный рисунокс велосипедистом. Велосипедист наклоняется в сторону поворота. Сила тяжести и сила реакции опоры со стороны земли дают равнодействующую силу, сообщающую центростремительное ускорение, необходимое для движения по окружности
Более подробно о записи уравнений. Если в некотором направлении тело двигается равномерно или покоится, то алгебраическая сумма (с учетом знаков) проекций сил равна нулю. Если в некотором направлении тело движется равноускоренно, то алгебраическая сумма проекций сил равна произведению массы на ускорение, согласно второму закону Ньютона.
Чтобы закрепить материал о силах, рассмотрим еще одну немного нестандартную ситуацию. Всем нам с детства знакомы басни И. Крылова. И мы предлагаем еще раз разобрать понятие равнодействующей силы .
Лебедь, Щука и Рак
Для начала о бозначим силы, выберем координатные оси.
(Обозначим все силы . Ось X напра вим слева направо, по направлени ю движения тела. Ось Y направим вве рх. )
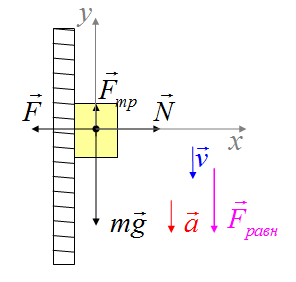
2)Тело, которое прижимают к вертикальной стенке, равноускоренно движется вниз. На тело действуют сила тяжести, сила трения, реакция опоры и сила, с которой прижимают тело. Вектор ускорения направлен вертикально вниз. Равнодействующая сила направлена вертикально вниз.

3)Тело равноускоренно движется по клину, наклон которого альфа. На тело действуют сила тяжести, сила реакции опоры, сила трения.


Видео:ЭТО ОБЯЗАТЕЛЬНО НУЖНО ЗНАТЬ — Второй Закон Ньютона или от чего зависит ускорение телаСкачать

Главное запомнить
1) Если тело покоится или движется равномерно, то равнодействующая сила равна нулю и ускорение равно нулю;
2) Если тело движется равноускоренно, значит равнодействующая сила не нулевая;
3) Направление вектора равнодействующей силы всегда совпадает с направлением ускорения;
4) Уметь записывать уравнения проекций действующих на тело сил
Второй закон Ньютона – это фундаментальный закон природы; он является обобщением опытных фактов, которые можно разделить на две категории:
Если на тела разной массы подействовать одинаковой силой, то ускорения, приобретаемые телами, оказываются обратно пропорциональны массам:
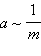
Если силами разной величины подействовать на одно и то же тело, то ускорения тела оказываются прямо пропорциональными приложенным силам:
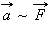
Обобщая подобные наблюдения, Ньютон сформулировал основной закон динамики:
Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение: 
Это и есть второй закон Ньютона. Он позволяет вычислить ускорение тела, если известна его масса m и действующая на тело сила 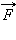
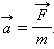 |
В Международной системе единиц (СИ) за единицу силы принимается сила, которая сообщает телу массой 1 кг ускорение 1 м/с 2 . Эта единица называется Н ьютоном (Н) . Ее принимают в СИ за эталон силы :
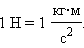 |
Если на тело одновременно действуют несколько сил (например, 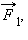
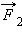
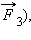
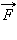
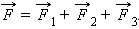 |
Если равнодействующая сила 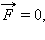
Особенностии второго закона Ньютона:
Видео:Алгоритм решения задач на второй закон Ньютона часть 1| Физика TutorOnlineСкачать

Второй закон Ньютона. Динамические уравнения движения
Второй закон Ньютона – основной закон динамики. Этот закон выполняется только в инерциальных системах отсчета.
Приступая к формулировке второго закона, следует вспомнить, что в динамике вводятся две новые физические величины – масса тела m и сила 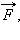
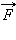
Второй закон Ньютона – это фундаментальный закон природы; он является обобщением опытных фактов, которые можно разделить на две категории:
- Если на тела разной массы подействовать одинаковой силой, то ускорения, приобретаемые телами, оказываются обратно пропорциональны массам:
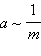 при F = const. при F = const. |
- Если силами разной величины подействовать на одно и то же тело, то ускорения тела оказываются прямо пропорциональными приложенн силам:
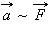 при m = const. при m = const. |
Обобщая подобные наблюдения, Ньютон сформулировал основной закон динамики:
Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение:
|
Это и есть второй закон Ньютона. Он позволяет вычислить ускорение тела, если известна его масса m и действующая на тело сила 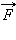
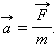 |
В Международной системе единиц (СИ) за единицу силы принимается сила, которая сообщает телу массой 1 кг ускорение 1 м/с 2 . Эта единица называется ньютоном (Н). Ее принимают в СИ за эталон силы (см. §1.7):
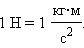 |
Если на тело одновременно действуют несколько сил (например, 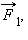
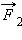
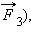
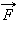
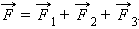 |
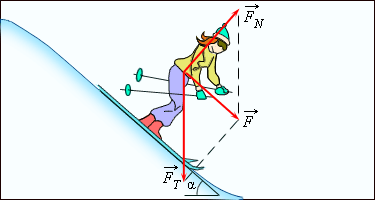 |
Рисунок 1.8.1. Сила 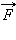 – равнодействующая силы тяжести – равнодействующая силы тяжести 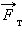 и силы нормального давления и силы нормального давления 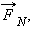 действующих на лыжницу на гладкой горе. Сила действующих на лыжницу на гладкой горе. Сила 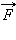 вызывает ускорение лыжника вызывает ускорение лыжника |
Если равнодействующая сила 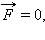
Второй закон Ньютона[править | править вики-текст]
Основная статья: Второй закон Ньютона
Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этогоускорением этой точки. Фактически, второй закон Ньютона вводит массу как меру проявления инертности материальной точки в выбранной инерциальной системе отсчёта (ИСО).
Масса материальной точки при этом полагается величиной постоянной во времени и независящей от каких-либо особенностей её движения и взаимодействия с другими телами [4][5][6][7] .
Современная формулировка[править | править вики-текст]
| В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе. |
При подходящем выборе единиц измерения, этот закон можно записать в виде формулы:
где 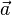
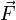
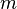
Второй закон Ньютона может быть также сформулирован в эквивалентной форме с использованием понятия импульс:
В инерциальной системе отсчета скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней внешних сил. 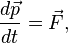 |
где 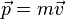
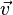
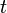
Иногда предпринимаются попытки распространить сферу применения уравнения 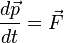
Замечания[править | править вики-текст]
Когда на материальную точку действуют несколько сил, с учётом принципа суперпозиции, второй закон Ньютона записывается в виде:
Второй закон Ньютона, как и вся классическая механика, справедлив только для движения тел со скоростями, много меньшими скорости света. При движении тел со скоростями, близкими к скорости света, используется релятивистское обобщение второго закона, получаемое в рамках специальной теории относительности.
Следует учитывать, что нельзя рассматривать частный случай (при 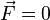
В уравнении движения динамической системы входит полный набор переменных, определяющий состояние этой системы (например, все координаты и скорости, или все координаты и импульсы), а также их производные по времени, что позволяет, зная такой набор в некий момент времени, вычислить его для момента времени, отстоящего на малый (бесконечно малый) промежуток времени. В принципе, повторяя этот процесс вычисления последовательно большое (бесконечное) количество раз, можно вычислить значение всех этих переменных для момента времени, как угодно далеко [2] отстоящего от начального. С помощью такого процесса можно (выбрав 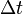
В современной квантовой теории термин уравнение движения нередко используется для обозначения именно только классических уравнений движения, то есть как раз для различения классического и квантового случая. В таком употреблении, например, слова «решение уравнений движения» означают именно классическое (неквантовое) приближение, которое может затем так или иначе использоваться при получении квантового результата или для сравнения с ним. В этом смыслеуравнения эволюции волновой функции не называют уравнениями движения, например упомянутые ниже уравнение Шредингера и уравнение Дирака нельзя назвать уравнением движения электрона. Определённую ясность тут вносит дополнение, указывающее на то, об уравнении движения чего идёт речь: так, хотя уравнение Дирака нельзя назвать уравнением движения электрона, его можно, даже в смысле, обсуждаемом в этом абзаце, назвать классическим уравнением движения спинорного поля.
| | | следующая лекция ==> |
| д) Исполнительные двигатели постоянного тока. | | |
Дата добавления: 2016-01-29 ; просмотров: 4552 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:1.4. Законы Ньютона как уравнение движения | Динамика | Александр Чирцов | ЛекториумСкачать

II Закон Ньютона.Динамические уравнения движения
Система отсчета, относительно которой выполняется закон Ньютона, называется инерциальной.
Второй закон Ньютона: изменение движения пропорционально приложенной силе и происходит в том направлении, в каком действует сила.
Сила – это физическая величина, характеризующая взаимодействие тел, в результате оторого тела приобретают ускорения или деформируются [F]=[Н]=[ 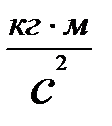
Но разные тела под влиянием одинаковых сил приобретают разные ускорения, следовательно, ускорение зависит не только от силы, но и от собственных свойств тел. Это свойство называется массой.
Масса – это мера инертности тела [m] = [кг].
Инертность – это способность тела приобретать ускорение.
1Н – сила, сообщающая телу массой 1кг ускорение 1м/с 2 в направлении действия силы.
Запишем второй закон Ньютона
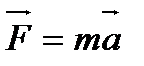
но 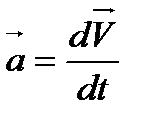
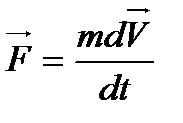
Подведем m под знак дифференциала
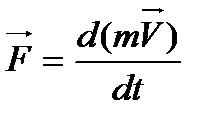
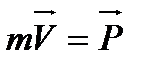
импульс (количество движения).
[Р]=[ 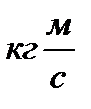
Перепишем второй закон Ньютона 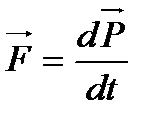

второй закон Ньютона через импульс
Динамические уравнения движения – это второй закон Ньютона, записанный для данного тела. Эти уравнения можно записать в векторном виде и в проекциях на оси координат. Составление и решение таких уравнений – главная задача динамики.
Движение твердого тела можно охарактеризовать двумя видами: поступательным и вращательным (из них состоит любое сложное движение).
При поступательном движении тела все его точки двигаются с одинаковыми скоростями и ускорениями. Если мысленно разбить тело наэлементами с массами Dmi, то по второму закону Ньютона получим
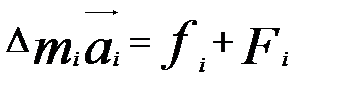
где fi – внутренняя сила (сила взаимодействия элементов тела);
Fi – внешняя сила, действующая на каждый элемент.
По третьему закону Ньютона сумма вех внутренних сил равна 0, поэтому, суммируя выражения, получим
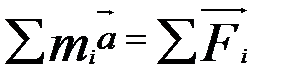
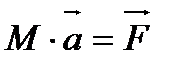
где 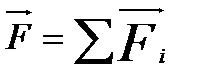
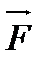
Следовательно, рассмотрение поступательного движения твердого тела можно заменить рассмотрением движения одной материальной точки с массой, равной массе тела, и находящейся под действием силы, равной главному вектору внешних сил.
При сложном движении тела все его точки имеют разные скорости и ускорения. Разобьем тело на столь малые элементы, что их скорости и ускорения остаются постоянными
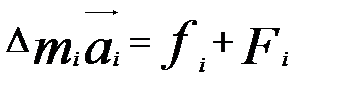
Суммируем это равенство fi = 0
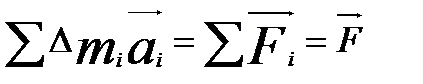
главный вектор внешних сил
Однако ускорения всех элементов тела разные, поэтому введем ускорение ас, определяемое равенством
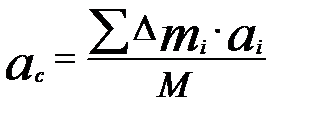
где М – масса всего тела.
Умножим левую и правую часть равенства на М, используя 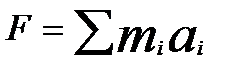
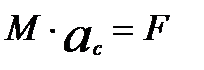
где ас – ускорение некоторой точкиС, координаты которой
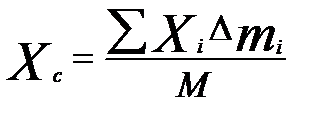

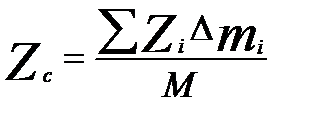
где С – центр масс тела или центр инерции (совпадает с центром приложения равнодействующей сил тяже).
15. Сложение двух гармонических колебаний одинаковой циклической частоты, происходящих вдоль одной прямой.
Пусть 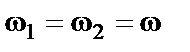
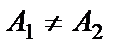
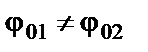
Складываемые колебания описываются уравнениями:
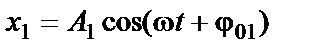
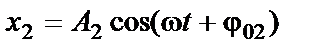
Так как колебания происходят вдоль одной прямой (вдоль оси 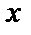
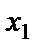
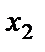
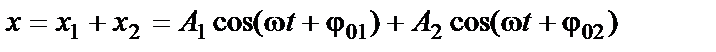
Выполним это сложение геометрически, с помощью векторов амплитуды 
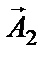
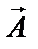
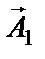
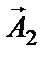
Проекции конца вектора 
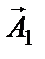
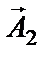
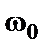
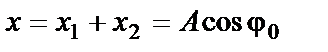
для произвольного момента времени:
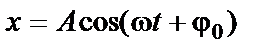
где 
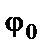
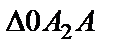

так как
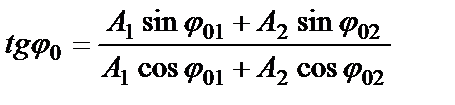
Амплитуда результирующего колебания зависит от разности фаз ( 
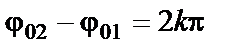
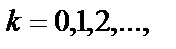

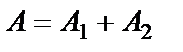

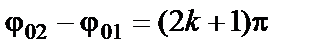
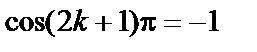
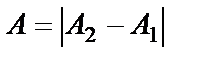
если разность фаз равна нечетному числу 
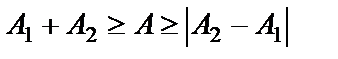
🌟 Видео
Три Закона Ньютона. Простое ОбъяснениеСкачать

Основное уравнение динамики вращательного движения. 10 класс.Скачать

6. Законы Ньютона. Уравнение движенияСкачать

Второй закон НьютонаСкачать

Взаимодействие тел. Второй закон Ньютона | Физика 10 класс #10 | ИнфоурокСкачать

Первый, второй, третий закон Ньютона. 10 класс.Скачать
Второй закон Ньютона | ЕГЭ по физике | #shortsСкачать

Второй закон Ньютона. Решение задач о движении тела. Урок 8. Физика 9 класс.Скачать

Физика - первый и второй законы НьютонаСкачать

Второй закон Ньютона | Физика 9 класс #11 | ИнфоурокСкачать

Урок 53. Простейшие задачи на законы НьютонаСкачать

ЧК_МИФ_1_2_2_2_1_(L3)__В ТОРОЙ ЗАКОН НЬЮТОНА КАК КЛАССИЧЕСКОЕ УРАВНЕНИЕ ДВИЖЕНИЯ...Скачать

Урок 51. Первый закон Ньютона. Взаимодействие тел и их ускорение.Скачать

ФИЗИКА 10 класс : Второй закон Ньютона. Сила. Принцип суперпозиции силСкачать

Второй закон движения Ньютона (видео 4) | Силы. Законы Ньютона | ФизикаСкачать

Удары, законы сохранения, узнаваемые уравнения движенияСкачать

Второй закон Ньютона на пальцах | ФизикаСкачать