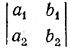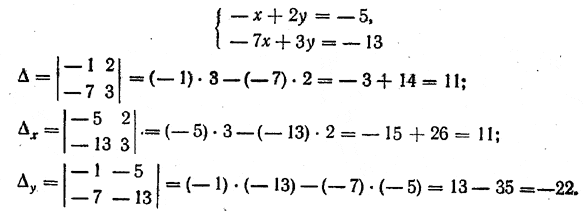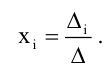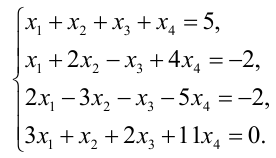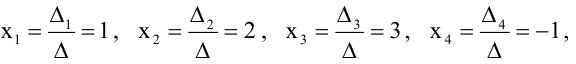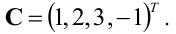Вспомогательный определитель крамеровской системы линейных уравнений получается из главного путем

Видео:Решение системы уравнений методом Крамера.Скачать

Вспомогательный определитель крамеровской системы линейных уравнений получается из главного путем

Дадим ряд необходимых определений.

Система линейных уравнений называется неоднородной, если хотя бы один ее свободный член отличен от нуля, и однородной, если все ее свободные члены равны нулю.

Решением системы уравнений называется упорядоченный набор чисел, который, будучи подставленным вместо переменных в систему, обращает каждое ее уравнение в тождество.

Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она решений не имеет.

Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Рассмотрим неоднородную систему линейных алгебраических уравнений, имеющую при n = m следующий общий вид:

Главной матрицей A системы линейных алгебраических уравнений называется матрица, составленная из коэффициентов, стоящих при неизвестных:

Определитель главной матрицы системы называется главным определителем и обозначается ∆.

Вспомогательный определитель ∆ _i получается из главного определителя путем замены i -го столбца на столбец свободных членов .

Теорема 1.1 (теорема Крамера). Если главный определитель системы линейных алгебраических уравнений отличен от нуля, то система имеет единственное решение, вычисляемое по формулам:

Если главный определитель ∆=0, то система либо имеет бесконечное множество решений (при всех нулевых вспомогательных определителях), либо вообще решения не имеет (при отличии от нуля хотя бы одного из вспомогательных определителей).

В свете приведенных выше определений , теорема Крамера может быть сформулирована иначе: если главный определитель системы линейных алгебраических уравнений отличен от нуля, то система является совместной определенной и при этом ; если главный определитель нулевой, то система является либо совместной неопределенной (при всех ∆ _i = 0), либо несовместной (при отличии хотя бы одного из ∆ _i от нуля).

После этого следует провести проверку полученного решения.

Пример 1.4. Решить систему методом Крамера

Решение. Так как главный определитель системы

отличен от нуля, то система имеет единственное решение. Вычислим вспомогательные определители

Воспользуемся формулами Крамера (1.6):

Пример 1.5. Данные дневной выручки молочного цеха от реализации молока, сливочного масла и творога за три дня продаж (на 2017 год) занесены в таблицу 1.4.

Определить стоимость 1 единицы продукции молокоцеха каждого вида.

Решение. Обозначим через x – стоимость 1 литра молока, y – 1 кг сливочного масла, z – 1 кг творога. Тогда, учитывая данные таблицы 1.4, выручку молочного цеха каждого из трех дней реализации можно отобразить следующей системой:

Решим систему методом Крамера. Найдем главный определитель системы по формуле (1.2):

Так как он отличен от нуля, то система имеет единственное решение. Вычислим вспомогательные определители с помощью формулы (1.2):

По формулам Крамера (1.6) имеем:

Вернувшись к обозначениям, видим, что стоимость 1 литра молока равна 44 рубля, 1 кг масла – 540 рублей, 1 кг творога – 176 рублей

Примечание. Как видно, процесс вычисления определителей вручную с помощью калькулятора трудоемок, поэтому на практике используют персональный компьютер. Так, для решения систем линейных алгебраических уравнений методом Крамера в MS Excel высчитывают ее главный и вспомогательные определители с использованием функции МОПРЕД( ), где аргументом является диапазон ячеек и элементы матрицы, определитель которой находится.

В MathCAD для нахождения определителя пользуются палитрой оператора Matrix

Видео:Решение системы трех уравнений по формулам КрамераСкачать

Вспомогательный определитель крамеровской системы линейных уравнений получается из главного путем

ЛИНЕЙНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА I

§29 Главный и вспомогательный определители системы двух линейных ypaвнений с двумя неизвестными.

Главным определителем системы уравнений

(1)

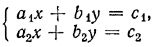
составленный из коэффициентов при неизвестных х и у. Этот определитель мы будем обозначать греческой буквой Δ (дельта). Очевидно, что

Первым вспомогательным определителем системы уравнений (1) называется определитель

Он получается из главного определителя этой системы уравнений путем замены первого столбца на столбец свободных членов. Этот определитель мы будем обозначать Δ_x. Индекс (то есть значок) х при Δ указывает, что в главном определителе Δ первый столбец, составленный из коэффициентов при х в системе уравнений (1), заменен на столбец свободных членов . Очевидно, что

Вторым вспомогательным определителем системы уравнений (1) называется определитель

‘

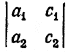
который получается из главного определителя этой системы путем замены второго столбца на столбец свободных членов. Этот определитель мы будем обозначать Δ_y. Очевидно, что

Пример. Для системы уравнений

Вопрос о том, какую пользу приносят введенные нами определители Δ , Δ_x и Δ_y при решении системы уравнений (1), мы выясним в следующих параграфах.

Найти главный и вспомогательные определители для следующих систем уравнений:

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Формулы Крамера — определение и вычисление с примерами решения

Содержание:

Формулы Крамера

Метод Крамера состоит в том, что мы последовательно находим главный определитель системы (5.3), т.е. определитель матрицы А

Формулы Крамера имеют вид:

Из (5.4) следует правило Крамера, которое дает исчерпывающий ответ на вопрос о совместности системы (5.3): если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по формулам:

Если главный определитель системы и все вспомогательные определители то система имеет бесчисленное множество решений. Если главный определитель системы а хотя бы один вспомогательный определитель отличен от нуля, то система несовместна.

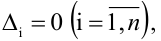
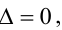
Пример:

Решить методом Крамера систему уравнений:

Решение:

Главный определитель этой системы 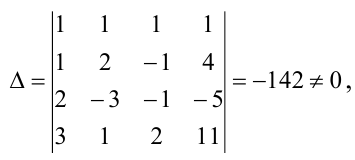значит, система имеет единственное решение.

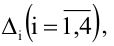
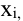
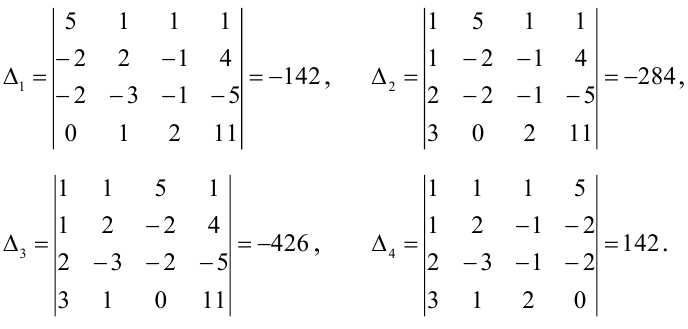
Вычислим вспомогательные определители получающиеся из определителя путем замены в нем столбца, состоящего из коэффициентов при столбцом из свободных членов:

Отсюда

решение системы — вектор

• Матричный метод
• Экстремум функции
• Методы решения систем линейных алгебраических уравнений (СЛАУ)
• Скалярное произведение и его свойства
• Уравнения прямых и кривых на плоскости
• Плоскость и прямая в пространстве
• Определитель матрицы
• Критерий совместности Кронекера-Капелли

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Решение системы уравнений методом Крамера 2x2Скачать

Метод Крамера решения систем линейных уравнений

Видео:Математика Без Ху!ни. Система линейных уравнений. Метод Крамера.Скачать

Формулы Крамера

Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.

Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.

Определение. Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

.

Формулы Крамера для нахождения неизвестных:

.

Найти значения и возможно только при условии, если

.

Этот вывод следует из следующей теоремы.

Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решить систему линейных уравнений:

. (2)

Согласно теореме Крамера имеем:

Итак, решение системы (2):

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором, решающим методом Крамера.

Видео:Решение системы уравнений методом ГауссаСкачать

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера, при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

*

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

* ,

** ,

т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

*

** .

Итак, система m линейных уравнений с n переменными называется несовместной, если у неё нет ни одного решения, и совместной, если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой, а более одного – неопределённой.

Видео:Решение систем линейных алгебраических уравнений методом Крамера.Скачать

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

.

На основании теоремы Крамера

………….
,

где
—

определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:

Пример 2. Решить систему линейных уравнений методом Крамера:

.

Решение. Находим определитель системы:

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором, решающим методом Крамера.

Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.

Пример 3. Решить систему линейных уравнений методом Крамера:

.

Решение. Находим определитель системы:

Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных

По формулам Крамера находим:

Итак, решение системы — (2; -1; 1).

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором, решающим методом Крамера.

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Применить метод Крамера самостоятельно, а затем посмотреть решения

Пример 4. Решить систему линейных уравнений:

.

Пример 5. Решить систему линейных уравнений методом Крамера:

.

Видео:2 минуты на формулы Крамера ➜ Решение систем уравнений методом КрамераСкачать

К началу страницы

Видео:Решение системы уравнений методом Крамера 4x4Скачать

Пройти тест по теме Системы линейных уравнений

Видео:Линейная алгебра, 8 урок, Метод КрамераСкачать

Продолжаем решать системы методом Крамера вместе

Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором, решающим методом Крамера.

В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных — буквы. За примерами далеко ходить не надо.

Пример 7. Решить систему линейных уравнений методом Крамера:

Здесь a — некоторое вещественное число. Решение. Находим определитель системы:

Находим определители при неизвестных

По формулам Крамера находим:

,

.

Следующий пример — на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

По формулам Крамера находим:

,

,

.

И, наконец, система четырёх уравнений с четырьмя неизвестными.

Пример 9. Решить систему линейных уравнений методом Крамера:

.

Внимание! Методы вычисления определителей четвёртого порядка здесь объясняться не будут. За этим — на соответствующий раздел сайта. Но небольшие комментарии будут. Решение. Находим определитель системы:

Небольшой комментарий. В первоначальном определителе из элементов второй строки были вычтены элементы четвёртой строки, из элементов третьей строки — элементы четвёртой строки, умноженной на 2, из элементов четвёртой строки — элементы первой строки, умноженной на 2. Преобразования первоначальных определителей при трёх первых неизвестных произведены по такой же схеме. Находим определители при неизвестных

Для преобразований определителя при четвёртом неизвестном из элементов первой строки были вычтены элементы четвёртой строки.

По формулам Крамера находим:

,

,

,

.

Итак, решение системы — (1; 1; -1; -1).

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором, решающим методом Крамера.

Самые внимательные, наверное, заметили, что в статье не было примеров решения неопределённых систем линейных уравнений. А всё потому, что методом Крамера решить такие системы невозможно, можно лишь констатировать, что система неопределённа. Решения таких систем даёт метод Гаусса.

🎬 Видео

Формулы Крамера для системы двух линейных уравненийСкачать

Крамера. Гаусса. Матричный метод. Система линейных уравнений. 3 способа решенияСкачать

Формулы КРАМЕРАСкачать

Решение систем уравнений. Метод Крамера для системы линейных уравнений с двумя неизвестными.Скачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Линейная алгебра: матрицы, определители, метод Крамера. Высшая математикаСкачать

10. Метод Крамера решения систем линейных уравнений.Скачать

Система 4x4. Решение по правилу Крамера.Скачать

Решение систем линейных уравнений, урок 2/5. Метод Крамера (метод определителей)Скачать