Все виды уравнений параболических цилиндров

Или цилиндры. Под цилиндром также понимают геометрическое тело.

И это не совсем то, что обычно подразумевает обыватель – класс цилиндрических поверхностей не ограничивается чёрным цилиндром на голове:

Задача 167

Построить поверхность, заданную уравнением

…что за дела?! Не опечатка ли здесь? Вроде как дано уравнение эллипса…

Нет, здесь не опечатка и все дела происходят именно в пространстве! Исследуем предложенную поверхность тем же методом, что использовали для плоскостей. Перепишем уравнение в виде , из которого следует, что «зет» принимает любые значения. Зафиксируем и построим в плоскости эллипс . Так как «зет» принимает все значения, то построенный эллипс непрерывно «тиражируется» вверх и вниз до бесконечности.

Данная поверхность называется эллиптическим цилиндром. Эллипс (на любой высоте) называется направляющей цилиндра, а параллельные прямые, проходящие через каждую точку эллипса называются образующими цилиндра (которые в прямом смысле слова его и образуют).

Ось является осью симметрии поверхности (но не её частью!).

Координаты любой точки, принадлежащей данной поверхности, обязательно удовлетворяют уравнению .

Пространственное неравенство задаёт «внутренность» бесконечной «трубы», включая саму цилиндрическую поверхность, и, соответственно, противоположное неравенство определяет множество точек вне цилиндра.

В практических задачах наиболее популярен частный случай, когда направляющей цилиндра является окружность:

Задача 168

Построить поверхность, заданную уравнением

Бесконечную «трубу» изобразить невозможно, поэтому художества ограничиваются, как правило, «обрезком».

Сначала удобно построить окружность радиуса в плоскости , а затем ещё пару окружностей сверху и снизу.

Полученные окружности (направляющие цилиндра) аккуратно соединяем 4 параллельными прямыми (образующими цилиндра):
Не забываем использовать пунктир для невидимых нам линий!

Координаты любой точки, принадлежащей данному цилиндру, удовлетворяют уравнению . Координаты любой точки, лежащей строго внутри «трубы», удовлетворяют неравенству , а неравенство задаёт множество точек внешней части. Для лучшего понимания рекомендую рассмотреть несколько конкретных точек пространства и убедиться в этом самостоятельно.

Часто эту поверхность некорректно называют круговым цилиндром. Круглым! Круговой цилиндр, строго говоря – есть тело, по той причине, что его направляющей является круг. И тело, кстати, определяется неравенством .

Задача 169

Построить поверхность и найти её проекцию на плоскость

Перепишем уравнение в виде , из которого следует, что «икс» принимает любые значения. Зафиксируем и в плоскости изобразим окружность – с центром в начале координат, единичного радиуса. Так как «икс» непрерывно принимает все значения, то построенная окружность порождает цилиндр с осью симметрии . Рисуем ещё одну окружность (направляющую цилиндра) и аккуратно соединяем их прямыми (образующими цилиндра). Местами получились накладки, но что делать, такой уж наклон:

На этот раз я ограничился кусочком цилиндра на промежутке и это не случайно. На практике зачастую и требуется изобразить лишь небольшой фрагмент поверхности.

Тут, к слову, получилось 6 образующих – две дополнительные прямые «закрывают» поверхность с левого верхнего и правого нижнего углов.

Теперь разбираемся с проекцией цилиндра на плоскость . Многие читатели понимают, что такое проекция, но, тем не менее, проведём очередную физкульт-пятиминутку:

Пожалуйста, встаньте и склоните голову над чертежом так, чтобы остриё оси смотрело перпендикулярно вам в лоб. То, чем с этого ракурса кажется цилиндр – и есть его проекция на плоскость . А кажется он бесконечной полосой, заключенным между прямыми , включая сами прямые. Данная проекция – это в точности область определения функций (верхний «жёлоб» цилиндра), (нижний «жёлоб»).

Давайте заодно проясним ситуацию и с проекциями на другие координатные плоскости. Пусть лучи солнца светят на цилиндр со стороны острия и вдоль оси . Тенью (проекцией) цилиндра на плоскость является аналогичная бесконечная полоса – часть плоскости , ограниченная прямыми ( – любое), включая сами прямые.

А вот проекция на плоскость несколько иная. Если смотреть на цилиндр из острия оси , то он спроецируется в окружность (не круг!) единичного радиуса , с которой мы начинали построение.

Задача 170

Построить поверхность и найти её проекции на координатные плоскости

Это задача для самостоятельного решения. Если условие не очень понятно, возведите обе части в квадрат и проанализируйте результат – выясните, какую именно часть цилиндра задаёт функция . Используйте методику построения, неоднократно применявшуюся выше. Краткое решение, чертёж и комментарии в конце книги.

Цилиндрические поверхности могут быть смещены относительно координатных осей, например:
– данное уравнение (по знакомым мотивам линий 2-го порядка) задаёт цилиндр единичного радиуса с линией симметрии, проходящей через точку параллельно оси .

Однако на практике подобные цилиндры попадаются довольно редко, и совсем уж невероятно встретить «косую» относительно координатных осей цилиндрическую поверхность.

Параболические цилиндры

Как следует из названия, направляющей такого цилиндра является парабола.

Задача 171

Построить поверхность и найти её проекции на координатные плоскости.

Не мог удержаться от этого примера =)

Решение: идём проторенной тропой. Перепишем уравнение в виде , из которого следует, что «зет» может принимать любые значения. Зафиксируем и построим обычную параболу на плоскости , предварительно отметив тривиальные опорные точки . Поскольку «зет» принимает все значения, то построенная парабола непрерывно «тиражируется» вверх и вниз до бесконечности. Откладываем такую же параболу, скажем, на высоте (в плоскости) и аккуратно соединяем их параллельными прямыми (образующими цилиндра):

Напоминаю полезный технический приём: если изначально нет уверенности в качестве чертежа, то линии сначала лучше прочертить тонко-тонко карандашом. Затем оцениваем качество эскиза, выясняем участки, где поверхность скрыта от наших глаз, и только потом придаём нажим грифелю.
Теперь вторая часть задания, отыскание проекций:

1) Проекцией цилиндра на плоскость является парабола .

2) Проекция цилиндра на плоскость представляет собой полуплоскость , включая ось

3) И, наконец, проекцией цилиндра на плоскость является вся плоскость .

Задача 172

Построить параболические цилиндры:

а) , ограничиться фрагментом поверхности в ближнем полупространстве;

б) на промежутке

В случае затруднений не спешим и рассуждаем по аналогии с предыдущими примерами, благо, технология досконально отработана. Не критично, если поверхности будут получаться немного корявыми – важно правильно отобразить принципиальную картину.

Я и сам особо не заморачиваюсь над красотой линий – если получился сносный чертёж «на троечку», обычно не переделываю. В образце решения, кстати, использован ещё один приём, позволяющий улучшить качество чертежа 😉

Гиперболические цилиндры

Направляющими таких цилиндров являются гиперболы.

Этот тип поверхностей, по моим наблюдениям, встречается значительно реже, и поэтому я ограничился единственным схематическим чертежом гиперболического цилиндра .

Принцип рассуждения здесь точно такой же – обычная «школьная» гипербола из плоскости непрерывно «размножается» вверх и вниз до бесконечности.

Видео:ВСЕ виды уравнений. Задание 5Скачать

Поверхности второго порядка: их виды, уравнения, примеры

Видео:Лекция 23. Виды уравнений прямой на плоскости.Скачать

Общее уравнение поверхности второго порядка и инварианты поворота и переноса декартовой прямоугольной системы координат

Общее уравнение поверхности второго порядка имеет вид

Для определения вида поверхности второго порядка по общему уравнению и приведения общего уравнения к каноническому, нам понадобятся выражения, которые называются инвариантами. Инварианты — это определители и суммы определителей, составленные из коэффициентов общего уравнения, которые не меняются при переносе и повороте системы координат. Эти инварианты следующие:

Следующие два выражения, называемые семиинвариантами, являются инвариантами поворота декартовой прямоугольной системы координат:

В случае, если I 3 = 0 , K 4 = 0 , семиинвариант K 3 будет также и инвариантом переноса; в случае же I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 = 0 семиинвариант K 2 = 0 будет также и инвариантом переноса.

Видео:Задание 9 на ОГЭ по математике 2023 / Разбираем все типы уравнений за 5 минут!Скачать

Виды поверхностей второго порядка и приведение общего уравнения поверхности второго порядка к каноническому

I. Если I 3 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

,

где λ 1 , λ 2 , λ 3 — корни характеристического уравнения

.

В зависимости от того, какие знаки у чисел λ 1 , λ 2 , λ 3 и K 4 /I 3 , определяется вид поверхности второго порядка.

Эллипсоид

Если числа λ 1 λ 2 , λ 3 одного знака, а K 4 /I 3 имеет знак им противоположный, то общее уравнение поверхности второго порядка определяет эллипсоид.

После решения характеристического уравнения общее уравнение можно переписать в следующем виде:

.

Тогда полуоси эллипсоида будут

, , .

Поэтому каноническое уравнение эллипсоида имеет вид

.

Мнимый эллипсоид

Если числа λ 1 λ 2 , λ 3 и K 4 /I 3 одного знака, то общее уравнение поверхности второго порядка определяет мнимый эллипсоид.

После решения характеристического уравнения общее уравнение можно привести к каноническому уравнению мнимого эллипсоида:

,

, , .

Мнимый конус

Если числа λ 1 λ 2 , λ 3 , а K 4 = 0 , то общее уравнение поверхности второго порядка определяет мнимый конус.

После решения характеристического уравнения общее уравнение можно привести к каноническому уравнению мнимого конуса:

,

, , .

Однополостный гиперболоид

Если два корня характеристического уравнения имеют один знак, а третий корень и K 4 /I 3 имеют знак, им противоположный, то общее уравнение поверхности второго порядка определяет однополостный гиперболоид.

Обозначая в этом случае через λ 1 и λ 2 корни характеристического уравнения, имеющие один знак, общее уравнение можно переписать в виде:

.

, , ,

то каноническое уравнение однополостного гиперболоида будет иметь вид

.

Двуполостный гиперболоид

Если два корня характеристического уравнения и K 4 /I 3 имеют один и тот же знак, а третий корень характеристического уравнения им противоположный, то общее уравнение поверхности второго порядка определяет двуполостный гиперболоид.

Обозначая в этом случае через λ 1 и λ 2 корни, имеющие один знак, общее уравнение можно переписать в виде:

.

Последняя запись и есть каноническое уравнение двуполостного гиперболоида.

Конус

Если два корня характеристического уравнения имеют один знак, третий корень имеет знак, им противоположный, а K 4 = 0 , то общее уравнение поверхности второго порядка определяет конус.

Считая, что одинаковый знак имеют корни λ 1 и λ 2 , общее уравнение можно переписать в виде:

,

известном как каноническое уравнение конуса.

II. Если I 3 = 0 , а K 4 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

,

где λ 1 и λ 2 — отличные от нуля корни характеристического уравнения.

Эллиптический параболоид

Если λ 1 и λ 2 имеют один знак, то общее уравнение поверхности второго порядка определяет эллиптический параболоид.

Общее уравнение можно переписать в виде:

.

Выбирая перед корнем знак, противоположный знаку λ 1 и λ 2 , и полагая

,

,

получим каноническое уравнение эллиптического параболоида:

.

Гиперболический параболоид

Если λ 1 и λ 2 имеют разные знаки, то общее уравнение поверхности второго порядка определяет гиперболический параболоид.

Обозначая через λ 1 положительный корень, а через λ 2 — отрицательный и беря перед корнем знак минус, переписываем уравнение в виде:

.

, ,

получим каноническое уравнение гиперболического параболоида:

.

III. Если I 3 = 0 , а K 4 = 0 , I 2 ≠ 0 то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

,

где λ 1 и λ 2 — отличные от нуля корни характеристического уравнения.

Эллиптический цилиндр

Если λ 1 и λ 2 одного знака, а K 3 /I 2 имеет знак, им противоположный, то общее уравнение поверхности второго порядка определяет эллиптический цилиндр.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

.

, ,

получим каноническое уравнение эллиптического цилиндра:

.

Мнимый эллиптический цилиндр

Если λ 1 , λ 2 и K 3 /I 2 одного знака, то общее уравнение поверхности второго порядка определяет мнимый эллиптический цилиндр.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

.

Последняя запись — каноническое уравнение мнимого эллиптического цилиндра.

Мнимые пересекающиеся плоскости

Если λ 1 и λ 2 имеют один знак, а K 3 = 0 , то общее уравнение поверхности второго порядка определяет две мнимые пересекающиеся плоскости.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

.

, ,

получим каноническое уравнение мнимых пересекающихся плоскостей:

.

Гиперболический цилиндр

Если λ 1 и λ 2 имеют разные знаки, а K 3 ≠ 0 , то общее уравнение поверхности второго порядка определяет гиперболический цилиндр.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

,

, .

Таким образом, каноническое уравнение гиперболического цилиндра:

.

Пересекающиеся плоскости

Если λ 1 и λ 2 имеют разные знаки, а K 3 = 0 , то общее уравнение поверхности второго порядка определяет две пересекающиеся плоскости.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

,

, .

Таким образом, пересекающихся плоскостей:

.

IV. Если I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

,

где λ 1 = I 1 — отличный от нуля корень характеристического уравнения.

Параболический цилиндр

Уравнение, получившееся после решения характеристического уравнения, можно переписать в виде:

,

.

Это уравнение параболического цилиндра, в каноническом виде оно записывается так:

.

V. Если I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 = 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

,

.

Параллельные плоскости

Если K 2 , то общее уравнение поверхности второго порядка определяет две параллельные плоскости.

,

перепишем его в виде

.

Мнимые параллельные плоскости

Если K 2 > 0 , то общее уравнение поверхности второго порядка определяет две мнимые параллельные плоскости.

,

перепишем его в виде

.

Совпадающие плоскости

Если K 2 = 0 , то общее уравнение поверхности второго порядка определяет две совпадающие плоскости:

.

Видео:Цилиндрические поверхностиСкачать

Решение примеров на определение вида поверхности второго порядка

Пример 1. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением

Решение. Найдём I 3 :

(как вычислить определитель).

I 1 = 1 + 5 + 1 = 7 ,

Следовательно, данная поверхность — однополостный гиперболоид.

.

Составляем и решаем характеристическое уравнение:

;

.

,

, , .

Пример 2. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением

Решение. Найдём I 3 :

.

.

Следовательно, общее уравнение определяет эллиптический параболоид.

.

I 1 = 2 + 2 + 3 = 7 .

Решаем характеристическое уравнение:

.

.

,

, .

Пример 3. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением

,

,

,

I 1 = 5 + 2 + 5 = 12 .

Так как I 3 = К 4 = 0 , I 2 > 0 , I 1 K 3 , то данное общее уравнение определяет эллиптический цилиндр.

.

.

Определить вид поверхности второго порядка самостоятельно, а затем посмотреть решение

Пример 4. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением

Видео:6-1. Уравнение теплопроводностиСкачать

3.5.6. Цилиндры второго порядка

В заключение обзора поверхностей второго порядка отметим еще случай, когда в уравнении отсутствует какая-нибудь координата. Такое уравнение определяет Цилиндрическую поверхность второго порядка (или Цилиндр) с образующими, параллельными той оси, координата которой в уравнении отсутствует.

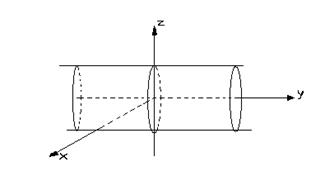
Так, поверхность, заданная уравнением

,

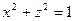
Является цилиндром с образующими, параллельными оси OY. Сечением цилиндра плоскостью XOZ является окружность с центром в начале координат и радиусом, равным единице
(рис. 16). Заметим, что уравнение цилиндра не отличается от уравнения окружности, называемой Направляющей для данного цилиндра.

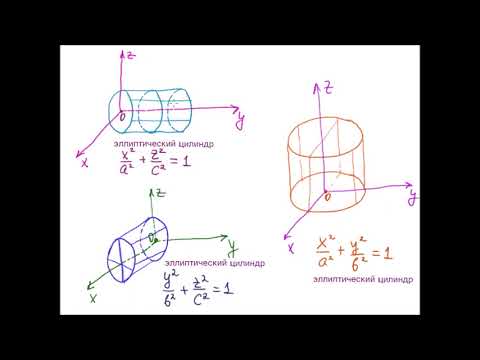
Среди цилиндров, образующие которых параллельны оси OZ различают цилиндры следующих типов:

А) эллиптический цилиндр

;

При = , получается круговой цилиндр

;

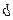
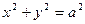
Б) гиперболический цилиндр

;

В) параболические цилиндры

или .

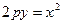
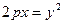
Тип цилиндра зависит от вида направляющей цилиндра в плоскости XOY (рис. 17)

🔥 Видео

Классические точные аналитические методы решения уравнений гиперболического и параболического типаСкачать

Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

§63 Цилиндрические поверхностиСкачать

Видеоурок по математике "Цилиндр"Скачать

Тихонов Н. А. - Методы математической физики - Классификация уравненийСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Принцип максимума для Параболического уравнения (Часть 1)Скачать

ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Параболические уравнения.Скачать

Повторяем решение уравнений. Полезно всем! Вебинар | МатематикаСкачать

Задание №9 на ОГЭ. Как решать уравнения? Какие типы будут?Скачать

Поверхности второго порядкаСкачать

Поверхности 2го порядка. КлассификацияСкачать