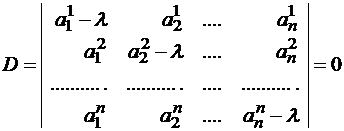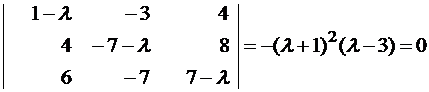Определение . Ненулевой вектор x называется собственным вектором оператора A , если оператор A переводит x в коллинеарный ему вектор, то есть A· x = λ· x . Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору x .
Отметим некоторые свойства собственных чисел и собственных векторов.
1. Любая линейная комбинация собственных векторов x 1, x 2, . x m оператора A , отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом.
2. Собственные векторы x 1, x 2, . x m оператора A с попарно различными собственными числами λ1, λ2, …, λm линейно независимы.
3. Если собственные числа λ1=λ2= λm= λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов.
Итак, если имеется n линейно независимых собственных векторов x 1, x 2, . x n, соответствующих различным собственным числам λ1, λ2, …, λn, то они линейно независимы, следовательно, их можно принять за базис пространства Rn. Найдем вид матрицы линейного оператора A в базисе из его собственных векторов, для чего подействуем оператором A на базисные векторы: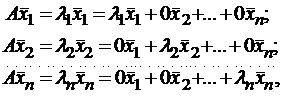 
тогда 
.
Таким образом, матрица линейного оператора A в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора A.
Существует ли другой базис, в котором матрица имеет диагональный вид? Ответ на поставленный вопрос дает следующая теорема.
Теорема. Матрица линейного оператора A в базисе < ε i> (i = 1..n) имеет диагональный вид тогда и только тогда, когда все векторы базиса — собственные векторы оператора A.
Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать
Правило отыскания собственных чисел и собственных векторов
Система (1) имеет ненулевое решение, если ее определитель D равен нулю
Пример №1 . Линейный оператор A действует в R3 по закону A· x =(x1-3x2+4x3, 4x1-7x2+8x3, 6x1-7x2+7x3), где x1, x2, . xn — координаты вектора x в базисе e 1=(1,0,0), e 2=(0,1,0), e 3=(0,0,1). Найти собственные числа и собственные векторы этого оператора.
Решение. Строим матрицу этого оператора:
A· e 1=(1,4,6)
A· e 2=(-3,-7,-7)
A· e 3=(4,8,7)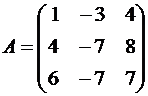 
.
Составляем систему для определения координат собственных векторов:
(1-λ)x1-3x2+4x3=0
x1-(7+λ)x2+8x3=0
x1-7x2+(7-λ)x3=0
Составляем характеристическое уравнение и решаем его:
Пример №2 . Дана матрица 
.
1. Доказать, что вектор x =(1,8,-1) является собственным вектором матрицы A. Найти собственное число, соответствующее этому собственному вектору.
2. Найти базис, в котором матрица A имеет диагональный вид.
Решение находим с помощью калькулятора.
1. Если A· x =λ· x , то x — собственный вектор
Определение . Симметрической матрицей называется квадратная матрица, в которой элементы, симметричные относительно главной диагонали, равны, то есть в которой ai k =ak i .
Замечания .
- Все собственные числа симметрической матрицы вещественны.
- Собственные векторы симметрической матрицы, соответствующие попарно различным собственным числам, ортогональны.
В качестве одного из многочисленных приложений изученного аппарата, рассмотрим задачу об определении вида кривой второго порядка.
Видео:Координаты вектора. 9 класс.Скачать
Раздел1 «Линейные пространства»
1. Проверить, является ли данное множество линейным пространством:
1.1. Множество всех векторов, параллельных фиксированной плоскости.
1.2. Множество всех векторов, параллельных фиксированной прямой.
1.3. Множество геометрических векторов а̅ (x,y,z), координаты которых удовлетворяют условию х+y+z=0.
1.4. Множество всех матриц размера 2×3.
1.5. Множество невырожденных матриц третьего порядка.
1.6. Множество вырожденных матриц третьего порядка.
1.7. Множество многочленов степени не выше третьей.
1.8. Множество многочленов Р(t)=a0+a1t+a2t 2 с положительными коэффициентами.
1.9. Множество расходящихся последовательностей.
1.10. Множество радиус-векторов, концы которых находятся на фиксированной прямой.
2. Доказать, что каждая из двух систем векторов образует базис и найти связь координат одного и того же вектора в этих двух базисах:
3. Векторы e̅1(1,1,1), e̅2(1,1,2), e̅3(1,2,3) и х̅(6,9,14) заданы своими координатами в некотором базисе. Показать, что векторы e̅1, e̅2, e̅3 образуют базис, и найти координаты вектора х̅ в этом базисе.
4. Доказать, что каждая из систем многочленов 1, х, х 2 и 1-х, 2х-х 2 , -3х образует базис в пространстве многочленов степени не выше второй, и найти матрицу перехода от первого базиса ко второму.
5. Как изменится матрица перехода от одного базиса к другому, если
— поменять местами два вектора первого базиса?
— поменять местами два вектора второго базиса?
6. В пространстве геометрических векторов V3 дана система векторов
e̅1= 2i̅ + j̅ — 3k̅, e̅2= 3i̅ + 2j̅ — 5k̅, e̅3= i̅ — j̅ + k̅. Доказать, что данная система образует базис в V3, составить матрицу перехода от базиса i̅ , j̅ , k̅ к базису e̅1, e̅2, e̅3 и найти координаты вектора х̅=6 i̅ +2 j̅ — 7k̅ в базисе e̅1, e̅2, e̅3.
7. Дана матрица перехода от базиса e̅1, e̅2, e̅3 к базису e̅1̍, e̅2̍, e̅3̍. Найти координаты векторов e̅1, e̅2, e̅3 в базисе e̅1̍, e̅2̍, e̅3̍.
8. Найти координаты многочлена t 2 -t+2 в базисе 1,t-1, (1-t) 2 .
9. Доказать, что если системы векторов
образуют базисы в пространстве Vn, то справедливо матричное равенство: Т Е→ Е̍ ̍ =Т Е→ Е̍ Т Е̍→ Е̍ ̍.
10. Установить, является ли изоморфизмом данное отображение V3 на R3:
10.1. φ(x i̅ +y j̅ +z k̅) = (2x –y, z, x+y+z)
10.2. φ(x i̅ +y j̅ +z k̅) = (x+y -1, 2z, 3y)
10.3. φ(x i̅ +y j̅ +z k̅) = (x+y, -y+2z, x+2y-2z)
Ответы к разделу 1
1. 1.1 является. 1.2. является. 1.3. является. 1.4 является. 1.5. не является. 1.6.не является. 1.7. является. 1.8.не является. 1.9.не является 1.10 является, если прямая проходит через начало координат
4. Матрица перехода
5. Поменяются местами две строки; поменяются местами два столбца.
9. Указание: воспользоваться определением матрицы перехода.
10. 10.1. является
10.2. не является, так как нарушено условие линейности отображения.
10.3. не является, так как нарушено условие взаимной однозначности отображения.
Раздел 2 «Линейные подпространства и линейные многообразия»
1. Проверить, являются ли заданные множества линейными подпространствами; указать какой-нибудь базис и размерность линейных подпространств:
1.1. Множество всех геометрических векторов из V3, компланарных фиксированной плоскости.
1.2. Множество геометрических векторов из V3, удовлетворяющих условию (͞х ,͞а)=0, где͞ а-фиксированный вектор.
1.3. Множество всех геометрических векторов из V3, удовлетворяющих условию | ̅х̅ | =1.
1.5. Множество всех симметрических матриц порядка n.
1.6. Множество решений линейной однородной системы уравнений
1.7. Множество всех векторов из Rn, координаты которых удовлетворяют условию: х1=хn.
2. Найти размерность линейной оболочки L(x̅1, x̅2) арифметических векторов x̅1(1, 0, 2, -1), x̅2(0, -1, 2, 0). Показать, что вектор x̅(1, -1, 4, -1) принадлежит оболочке.
3. Найти размерность и какой-нибудь базис линейной оболочки заданной системы векторов x̅1(1, 0, 0, -1), x̅2(2, 1, 1, 0), x̅3(1, 1, 1, 1), x̅4(1, 2, 3, 4), x̅5(0, 1, 2, 3).
4. Найти размерность и какой-нибудь базис линейной оболочки заданной системы векторов x̅1(1, 1, 1, 1, 0), x̅2(1, 1, -1, -1, -1), x̅3(2, 2, 0, 0, -1), x̅4(1, 1, 5, 5, 2), x̅5(1, -1, -1, 0, 0).
5. Найти размерность суммы и пересечения линейных оболочек L(x̅1, x̅2) и L(y̅1, y̅2):
6. Найти размерность суммы и пересечения линейных оболочек L(x̅1, x̅2, x̅3) и L(y̅1, y̅2):
7. Написать уравнение геометрического образа линейной оболочки
L(а̄) и многообразия L(а̄) +b̅, если а̄= -2i̅ + j̅ — k̅, b̅= 2i̅ — j̅.
8. Написать уравнение геометрического образа линейной оболочки
L(а̄1, a̅2) и многообразия L(а̄1, a̅2) + b̅, если а̄1= -i̅ + j̅ + k̅, а̄2=2 j̅ — k̅ b̅= i̅ + k̅.
9. Задана система уравнений
Доказать, что множество решений этой системы есть линейное многообразие в пространстве R5.Сдвигом какого подпространства получается это линейное многообразие? Найти ранг и какой-нибудь базис этого подпространства. Найти какой-нибудь вектор сдвига.
Ответы к разделу 2
1. 1.2. является, dimL=1, 1.3.не является, 1.4. является, dimL=n-2, 1.5. является, dimL=n 2 — Cn 2 , 1.6. является, dimL=3, 1.7.является, dimL=n-1
5. Размерность пересечения равна 1, базисный вектор имеет координаты z̅ (5, -2, -3, -4); размерность суммы равна 3, базис составлен, например, из векторов z̅, x̅1, y̅1.
6. Сумма совпадает с первым пространством, пересечение – со вторым.
7. Линейная оболочка – прямая, проходящая через точку (0, 0, 0) параллельно вектору с координатами (-2, 1, -1), линейное многообразие — прямая, проходящая через точку (2,-1, 0) параллельно вектору с координатами (-2, 1, -1)
8. Линейная оболочка – плоскость -3x – y — 2z =0, линейное многообразие – плоскость -3x – y — 2z + 5=0.
9. Множество решений неоднородной системы есть линейное многообразие, полученное из подпространства размерности 3 решений соответствующей однородной системы сдвигом на произвольное частное решение неоднородной системы.
10. Доказать, что пространство Rn есть прямая сумма двух линейных подпространств: L1, заданного уравнением х1+х2+…+хn=0 и L2, заданного системой уравнений х1=х2=…=хn.
11. Пусть линейное пространство L является прямой суммой линейных подпространств L1 и L2. Доказать, что размерность L равна сумме размерностей подпространств L1 и L2, причем любые базисы L1 и L2 дают вместе базис L.
12. Доказать, что сумма L линейных подпространств L1 и L2 тогда и только тогда будет прямой суммой, когда хотя бы один вектор x̅, принадлежащий L, представляется в виде x̅= x̅1+ x̅2, где x̅1 принадлежит L1, x̅2 принадлежит L2.
Раздел3 «Евклидовы пространства»
1. Пусть͞ х( х1, х2), ȳ(y1, y2) — произвольные векторы арифметического пространства R2. Проверить, можно ли следующими способами определить скалярное произведение в R2:
Записать неравенство Коши – Буняковского в тех случаях, где это возможно.
2. Доказать, что в пространстве многочленов не выше n-1 степени скалярное произведение многочленов
можно определить следующим способом:
Написать неравенство Коши – Буняковского, неравенства треугольника для этого пространства.
3. Найти нормированный вектор, ортогональный к векторам: (1,1,1,1), (1,-1,-1,1), (2,1,1,3).
4. Проверить, что векторы следующей системы попарно ортогональны:
5. Построить ортонормированный базис пространства, приняв за два вектора этого базиса векторы (1∕ 2, 1∕ 2, 1∕ 2, 1∕ 2) и (1∕6, 1∕6, 1∕2, -5∕6).
6. Посредством процесса ортогонализации, найти ортогональный базис подпространства, натянутого на данные системы векторов:
7. Проверить ортогональность следующей системы векторов и дополнить ее до ортогонального базиса:
8. Найти ортогональную проекцию и ортогональную составляющую вектора x̅(4,-1,-3,4) на линейное подпространство L, натянутое на векторы ē1(1,1,1,1), ē2(1,2,2,-1), ē3(1,0,0,3).
9. Найти базис ортогонального дополнения подпространства L, натянутого на векторы:
10. Доказать, что в действительном евклидовом пространстве справедлива теорема Пифагора, а также ей обратная: два вектора x̅ и y̅ ортогональны тогда и только тогда, когда | x̅ — y̅ | 2 = | x̅ | 2 + | y̅ | 2 .
Ответы к разделу 3
1. 1.1.можно, 1.2.нельзя
5. За остальные два вектора можно взять, например, 1∕√26(0, -4, 3, 1) и 1∕√234(-13, 5, 6, 2).
8. Ортогональная проекция (1,-1,-1,5), ортогональная составляющая (3,0,-2,-1)
9. Базис ортогонального дополнения (2,-2,-1,0), (1,1,0,-1)
Раздел4 «Линейные операторы»
1. Установить, какие из заданных отображений пространства V3 являются линейными операторами, выписать их матрицы в базисе i̅ , j̅, k̅:
1.2. Аx̅ = λx̅ +a̅, λ и a̅ фиксированы.
1.3. Аx̅ =( x̅, e̅) e̅, где e̅ — заданный единичный вектор.
1.4. Аx̅ = [ a̅, x̅], где a̅- фиксированный вектор.
1.5. Аx̅ = (y+z) i̅ + (2x+z) j̅ +(3x-y+z) k̅, где x̅ = x i̅ +y j̅ +z k̅.
2. Установить, какие из заданных отображений пространства арифметических векторов R3 в себя являются линейными, выписать их матрицы в каноническом базисе:
3. Показать, что дифференцирование является линейным преобразованием пространства всех многочленов степени не выше n от одного неизвестного с вещественными коэффициентами, найти матрицу этого преобразования в базисе 1,х, х 2 ,…х n .
4. В пространстве L4 задан линейный оператор, матрица которого в некотором базисе e̅1, e̅2, e̅3, e̅4 равна
5. В пространстве L3 заданы два базиса:
Найти матрицу оператора в базисе e̅1̍ ̍, e̅2̍ ̍, , e̅3̍ ̍, если его матрица в базисе e̅1̍, e̅2̍, e̅3̍ имеет вид
6. В пространстве L2 оператор А в базисе a̅1(1,2), a̅2(2,3) имеет матрицу
а оператор В в базисе b̅1(3,1), b̅2(4,2) имеет матрицу
Найти матрицу оператора А+В в базисе b̅1, b̅2.
7. Описать ядро и образ линейного оператора, действующего в пространстве V3: Аx̅ =( x̅, e̅) e̅, где e̅ — заданный единичный вектор.
8. Описать ядро и образ линейного оператора, действующего в пространстве V3: Аx̅ = [ a̅, x̅], где a̅- фиксированный вектор.
9. Для линейного оператора, действующего в пространстве R3, определить ранг и дефект, а также найти базисы ядра и образа:
10. Доказать, что оператор невырожденный тогда и только тогда, когда его дефект равен нулю, а, следовательно, ранг совпадает с размерностью пространства.
11. Найти собственные значения и собственные векторы оператора проектирования на плоскость Oxy в пространстве V3.
12. Найти собственные значения и собственные векторы оператора, заданного матрицей в некотором фиксированном базисе:
13. Найти собственные значения и собственные векторы оператора, заданного матрицей в некотором фиксированном базисе:
14. Найти собственные значения и собственные векторы оператора, заданного матрицей в некотором фиксированном базисе:
15. Выяснить, какие из матриц линейных операторов можно привести к диагональному виду путем перехода к новому базису, найти этот базис и соответствующую ему матрицу:
Ответы к разделу 4
1. 1.1.является, матрица оператора
1.3.является оператором проектирования на ось
1.4.является, если a̅ = a1i̅ +a2j̅ +a3k̅, то матрица перехода
1.5. является, матрица оператора
2. 2.1.является, матрица оператора
2.3. является, матрица оператора
3. матрица оператора
4. Матрица оператора
5. Матрица оператора в базисе e̅1̍ ̍, e̅2̍ ̍, , e̅3̍ ̍ имеет вид
6.Матрица оператора А+В
7. Ядро оператора — двумерное подпространство векторов, ортогональных вектору e̅, образ оператора — одномерное подпространство векторов, коллинеарных вектору e̅.
8. Ядро оператора — одномерное подпространство векторов, коллинеарных вектору a̅, образ оператора — двумерное подпространство векторов, ортогональных вектору a̅.
9. Дефект оператора равен 1, ранг оператора равен 2. В качестве базиса
образа оператора могут быть выбраны, например, векторы e̅1(1,1,1), e̅2(2,0,1,), в качестве базиса ядра оператора может быть выбран, например, вектор e̅(1,-1,1).
11.λ1=1, собственные векторы– векторы, компланарные плоскости Oxy; λ2=0, собственные векторы- векторы, ортогональные плоскости Oxy.
Базис образуют, например, векторы e̅1(1,1,1), e̅2(1,0,0), e̅3(1,0,-3).
16. Матрица к диагональному виду не приводится.
Раздел 5 «Линейные операторы в пространстве со скалярным произведением»
1. Линейный оператор А в базисе e̅1(1,0), e̅2(1,1) имеет матрицу
Найти матрицу сопряженного оператора в базисе e̅1, e̅2, если векторы e̅1, e̅2 заданы своими координатами в некотором ортонормированном базисе.
2. Линейный оператор А в базисе e̅1(1,2,1), e̅2(1,1,2), e̅3(1,1,0) имеет матрицу
Найти матрицу сопряженного оператора в базисе e̅1, e̅2, e̅3, если векторы e̅1, e̅2, e̅3 заданы своими координатами в некотором ортонормированном базисе.
3. Вычислить А n , если
4. Доказать, что операция * перехода от оператора А к сопряженному оператору А* обладает следующими свойствами
5. В пространстве многочленов степени не выше второй задано скалярное произведение: (f,g)=a0b0+a1b1+a2b2, где f(t)=a0+a1t+a2t 2 . Найти матрицы оператора дифференцирования D и сопряженного оператора D* в базисе 0.5t 2 -0.5t, t 2 -1, 0.5t 2 +0.5t.
6. Выяснить, можно ли с помощью перехода к новому базису диагонализировать оператор А, заданный своей матрицей в некотором фиксированном базисе. Найти этот базис и соответствующую ему диагональную форму матрицы
7. Найти ортонормированный базис из собственных векторов и матрицу в этом базисе для линейного оператора, заданного в некотором ортонормированном базисе матрицей
🔥 Видео
Векторы. Метод координат. Вебинар | МатематикаСкачать
Базис и матрица перехода. Координаты вектора в разных базисах.Скачать
Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать
Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать
Координаты вектора в пространстве. 11 класс.Скачать
Высшая математика. Линейные пространства. Векторы. БазисСкачать
Разложение вектора по векторам (базису). Аналитическая геометрия-1Скачать
Найдите разложение вектора по векторам (базису)Скачать
Как разложить вектор по базису - bezbotvyСкачать
Образуют ли данные векторы базисСкачать
Векторное произведение векторов | Высшая математикаСкачать
Линейная зависимость векторовСкачать
Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать
Векторы #3: многомерные системы координат, базисные векторыСкачать
Векторы #2: скалярное произведение векторов, системы координатСкачать
Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать
Разложение вектора по базису. 9 класс.Скачать
Координаты вектора в базисе. Собственные числа и векторы (решение задач)Скачать
