В этой статье и постараюсь объяснить 2 способа отбора корней в тригонометрическом уравнение: с помощью неравенств и с помощью тригонометрической окружности. Перейдем сразу к наглядному примеру и походу дела будем разбираться.
а) Решить уравнение sqrt(2)cos^2x=sin(Pi/2+x)
б) Найдите все корни этого уравнения, принадлежащие промежутку [-7Pi/2; -2Pi]
Решим пункт а.
Воспользуемся формулой приведения для синуса sin(Pi/2+x) = cos(x)
sqrt(2)cos^2x — cosx = 0
cosx(sqrt(2)cosx — 1) = 0
x1 = Pi/2 + Pin, n ∈ Z
sqrt(2)cosx — 1 = 0
x2 = arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x3 = -arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x2 = Pi/4 + 2Pin, n ∈ Z
x3 = -Pi/4 + 2Pin, n ∈ Z
Решим пункт б.
1) Отбор корней с помощью неравенств
Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [-7Pi/2; -2Pi], находим целые значения для n.
-7Pi/2 меньше или равно Pi/2 + Pin меньше или равно -2Pi
Сразу делим все на Pi
-7/2 меньше или равно 1/2 + n меньше или равно -2
-7/2 — 1/2 меньше или равно n меньше или равно -2 — 1/2
-4 меньше или равно n меньше или равно -5/2
Целые n в этом промежутку это -4 и -3. Значит корни принадлежащие этому промежутку буду Pi/2 + Pi(-4) = -7Pi/2, Pi/2 + Pi(-3) = -5Pi/2
Аналогично делаем еще два неравенства
-7Pi/2 меньше или равно Pi/4 + 2Pin меньше или равно -2Pi
-15/8 меньше или равно n меньше или равно -9/8
Целых n в этом промежутке нет
-7Pi/2 меньше или равно -Pi/4 + 2Pin меньше или равно -2Pi
-13/8 меньше или равно n меньше или равно -7/8
Одно целое n в этом промежутку это -1. Значит отобранный корень на этом промежутку -Pi/4 + 2Pi*(-1) = -9Pi/4.
Значит ответ в пункте б: -7Pi/2, -5Pi/2, -9Pi/4
2) Отбор корней с помощью тригонометрической окружности
Чтобы пользоваться этим способом надо понимать как работает эта окружность. Постараюсь простым языком объяснить как это понимаю я. Думаю в школах на уроках алгебры эта тема объяснялась много раз умными словами учителя, в учебниках сложные формулировки. Лично я понимаю это как окружность, которую можно обходить бесконечное число раз, объясняется это тем, что функции синус и косинус периодичны.
Обойдем раз против часовой стрелки
Обойдем 2 раза против часовой стрелки
Обойдем 1 раз по часовой стрелки (значения будут отрицательные)
Вернемся к нашем вопросу, нам надо отобрать корни на промежутке [-7Pi/2; -2Pi]
Чтобы попасть к числам -7Pi/2 и -2Pi надо обойти окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.
Рассмотри x = Pi/2 + Pin. Какой приблизительно должен быть n, чтобы значение x было где-то в этом промежутке? Подставляем, допустим -2, получаем Pi/2 — 2Pi = -3Pi/2, очевидно это не входит в наш промежуток, значит берем меньше -3, Pi/2 — 3Pi = -5Pi/2, это подходит, попробуем еще -4, Pi/2 — 4Pi = -7Pi/2, также подходит.
Рассуждая аналогично для Pi/4 + 2Pin и -Pi/4 + 2Pin, находим еще один корень -9Pi/4.
Сравнение двух методов.
Первый способ (с помощью неравенств) гораздо надежнее и намного проще для пониманию, но если действительно серьезно разобраться с тригонометрической окружностью и со вторым методом отбора, то отбор корней будет гораздо быстрее, можно сэкономить около 15 минут на экзамене.
- Определите число корней уравнения, принадлежащих промежутку [0 ; 2pi] используя граффик функции y = cos x(1 — tg ^ 2x) / (1 + tg ^ 2x) = 1 / 5Пожалуйста распишите решение?
- Б)Найдите все корни этого уравнения, принадлежащие промежутку ( ; )?
- Найдите сумму корней уравнения cos(x + 2000π) = 0, принадлежащих промежутку [0 ; 2π]?
- Помогите найти корни уравнения 2cosx = 1 принадлежащие промежутку (0 ; пи / 2] С полным решением?
- Найдите корни уравнения cosx — cos 2x = 1, принадлежащие промежутку ( — 3Pi / 4 ; Pi ]?
- Найдите корни уравнения sin 5x + sin x = cos 2x принадлежащие промежутку [ — ; ]?
- Решите уравнение Найдите все корни этого уравнения, принадлежащие промежутку?
- Найдите корни уравнения sin 5x + sin x = cos 2x принадлежащие промежутку [ — ; ]?
- Интервалы уравнения с промежутками Решением уравнения cos ^ 2 x + sin x + 1 = 0 в промежутке [0 ; 2π] есть : Распишите пожалуйста?
- Пожалуйста, помогите решить уравнение sin ^ 2(2x) + cos ^ 2(5x) = 1 надо указать число решений этого ур — я, принадлежащих промежутку (0 ; 4п)?
- Sin²2x + cos²5x = 1?
- Отбор корней в тригонометрических уравнениях
- 🔍 Видео
Видео:Отбор корней по окружностиСкачать

Определите число корней уравнения, принадлежащих промежутку [0 ; 2pi] используя граффик функции y = cos x(1 — tg ^ 2x) / (1 + tg ^ 2x) = 1 / 5Пожалуйста распишите решение?
Алгебра | 10 — 11 классы
Определите число корней уравнения, принадлежащих промежутку [0 ; 2pi] используя граффик функции y = cos x
(1 — tg ^ 2x) / (1 + tg ^ 2x) = 1 / 5
Пожалуйста распишите решение.
Конечный ответ 4.
(cos²x — sin²x) / cos²x : cos²x + sin²x) / cos²x = cos²x — sin²x) / cos²x * cos²x = cos2x = 1 / 5
2x = + — arccos1 / 5 + 2πn
x = + — 1 / 2arccos1 / 5 + πn
x1 = 1 / 2arccos1 / 5
x2 = π — 1 / 2arccos1 / 5
x3 = π + 1 / 2arccos1 / 5
x4 = 2π — 1 / 2arccos1 / 5.
Видео:Отбор корней по окружностиСкачать

Б)Найдите все корни этого уравнения, принадлежащие промежутку ( ; )?
Б)Найдите все корни этого уравнения, принадлежащие промежутку ( ; ).
Видео:Три способа отбора корней в задании 13 ЕГЭ профильСкачать

Найдите сумму корней уравнения cos(x + 2000π) = 0, принадлежащих промежутку [0 ; 2π]?
Найдите сумму корней уравнения cos(x + 2000π) = 0, принадлежащих промежутку [0 ; 2π].
Видео:3,5 способа отбора корней в тригонометрии | ЕГЭ по математике | Эйджей из ВебиумаСкачать

Помогите найти корни уравнения 2cosx = 1 принадлежащие промежутку (0 ; пи / 2] С полным решением?
Помогите найти корни уравнения 2cosx = 1 принадлежащие промежутку (0 ; пи / 2] С полным решением.
Ответ записать в градусах.
Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Найдите корни уравнения cosx — cos 2x = 1, принадлежащие промежутку ( — 3Pi / 4 ; Pi ]?
Найдите корни уравнения cosx — cos 2x = 1, принадлежащие промежутку ( — 3Pi / 4 ; Pi ].
Видео:Нахождение корней уравнения, принадлежащих промежуткуСкачать

Найдите корни уравнения sin 5x + sin x = cos 2x принадлежащие промежутку [ — ; ]?
Найдите корни уравнения sin 5x + sin x = cos 2x принадлежащие промежутку [ — ; ].
Видео:N 35 Алгебра 11 класс КолягинСкачать

Решите уравнение Найдите все корни этого уравнения, принадлежащие промежутку?
Решите уравнение Найдите все корни этого уравнения, принадлежащие промежутку.
Видео:Нахождение корней уравнения, принадлежащих промежуткуСкачать

Найдите корни уравнения sin 5x + sin x = cos 2x принадлежащие промежутку [ — ; ]?
Найдите корни уравнения sin 5x + sin x = cos 2x принадлежащие промежутку [ — ; ].
Видео:Находим решение тригонометрического уравнения на интервале Алгебра 10 классСкачать

Интервалы уравнения с промежутками Решением уравнения cos ^ 2 x + sin x + 1 = 0 в промежутке [0 ; 2π] есть : Распишите пожалуйста?
Интервалы уравнения с промежутками Решением уравнения cos ^ 2 x + sin x + 1 = 0 в промежутке [0 ; 2π] есть : Распишите пожалуйста.
Видео:Задание №13. Как отбирать корни в тригонометрической окружности? 🤔Скачать

Пожалуйста, помогите решить уравнение sin ^ 2(2x) + cos ^ 2(5x) = 1 надо указать число решений этого ур — я, принадлежащих промежутку (0 ; 4п)?
Пожалуйста, помогите решить уравнение sin ^ 2(2x) + cos ^ 2(5x) = 1 надо указать число решений этого ур — я, принадлежащих промежутку (0 ; 4п).
Видео:Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать

Sin²2x + cos²5x = 1?
Sin²2x + cos²5x = 1.
В ответе укажите число решений этого уравнения, принадлежащих промежутку (0 ; 4п).
Вы зашли на страницу вопроса Определите число корней уравнения, принадлежащих промежутку [0 ; 2pi] используя граффик функции y = cos x(1 — tg ^ 2x) / (1 + tg ^ 2x) = 1 / 5Пожалуйста распишите решение?, который относится к категории Алгебра. По уровню сложности вопрос соответствует учебной программе для учащихся 10 — 11 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.
6, (1)>6, 1 6, (1) = 6 1 / 9 = 55 / 9.
5 / 9. Лалалалалаллатклад.
A)(3√6 + 2√2) / (3√2 + 2) = (3√2 * √3 + 2√2) / (3√3 + 2) = √2 * (3√3 + 2) / (3√3 + 2) = √2. B)(∛24 + ∛81 + ∛3) / (6¹ / ⁴ * (27 / 3)¹ / ⁶. Упростим числитель : ∛(3 * 8) + ∛(3 * 27) + ∛3 = ∛(3 * 2³) + ∛3 * 3³ + ∛3 = 2 * ∛3 + 3 * ∛3 + ∛3 = ∛3 * (2 + 3..
Сумма 2 — х углов пар — ма равна 180 градусов.
A + b = 180 a — b = 30 a = 30 + b 30 + b + b = 180 2b = 150 b = 75 a = 75 + 30 = 105.
Нужно взять х кг первого сплава и у кг второго. Х + у = 6 В х кг первого сплава содержится х / 5 кг золота и 4х / 5 кг серебра В у кг второго сплава содержится 2у / 5 кг золота и 3у / 5 серебра. В 6 кг нового сплава должно содержаться 3 * 6 / 10 = ..
Нули функции — это значения аргумента, при которых функция y равна нулю. Y = 0 y = x² — 49 x² — 49 = 0 x² = 49 x1 = + √49 = + 7 x2 = — √49 = — 7 Нули функции x = 7 и x = — 7.
(2²)³ = 2 ^ 6 = 64 3² * 3 * 3³ = 3 ^ 6 = 81 * 9 = 729 (0. 3) ^ 8 / (0. 3) ^ 5 = 0. 3 ^ 3 = 0. 027 12. 5³ * 8³ = (12. 5 * 8)³ = 100³ = 1000000.
1) (2²)³ = 2 ^ 6 = 64 2) 3² * 3 * 3³ = 3 ^ 6 = 729 3) 0, 3 ^ 8 / 0, 3 ^ 5 = 0, 3³ = 0, 027 4) 12, 5³ * 8³ = (12, 5 * 8)³ = 100³ = 1 000 000.
Луч t делит угол на 7 равных частей(5 + 2) отсюда hq / 7 = 77 / 7 = 11 th = 11 * 2 = 22 tq = 11 * 5 = 55.
Видео:Методы отбора корней тригонометрического уравненияСкачать

 Отбор корней в тригонометрических уравнениях
Отбор корней в тригонометрических уравнениях
Практика приемных экзаменов в вузы показывает, что при решении тригонометрических уравнений абитуриенты нередко затрудняются как в выборе способа решения уравнения, так и при отборе его корней.
Проблема отбора корней, отсеивания лишних корней при решении тригонометрических уравнений специфична. Лишние корни могут появиться вследствие того, что в процессе решения произошло расширение области определения уравнения. Запись ответа тригонометрического уравнения часто связана с понятиями объединения и пересечения множеств. Обычно при решении таких уравнений получают серии корней, и в окончательном варианте ответ записывают в виде объединения этих серий. Но как быть, если эти серии пересекаются? Надо ли исключать повторяющиеся корни решения или этого можно не делать?
С понятием пересечения множеств связан и еще один важный вопрос: в ответе не должно быть значений переменной, при которых выражения в левой или правой частях уравнения не определены. Такие значения надо исключить. Для этого надо уметь находить пересечение различных серий.
В предлагаемой работе на конкретных примерах рассматриваются различные способы и приемы при выборе ответа. Надеемся, что данная работа поможет учителям старших классов и самим учащимся при подготовке к вступительным экзаменам в вузы.
1. Отбор чисел на тригонометрическом круге
Проблему отбора корней, отсеивания лишних корней при решении тригонометрических уравнений часто можно решить с помощью изображения чисел на тригонометрическом круге. В ряде случаев этот прием, на наш взгляд, более наглядный и убедительный.
Пример 1. cos x + cos 2x – cos 3x = 1.
2sin x sin 2x – 2sin 2 x = 0,

Из рис. 1 видно, что серия x3(*) включает в себя один из корней серии x1( · ).
Ответ:
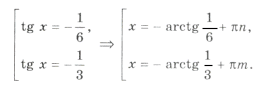
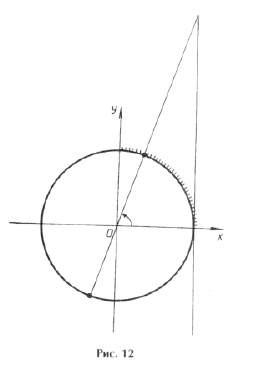
Пример 2. tg x + tg 2x – tg 3x = 0.
Серия x2(*) не удовлетворяет ОДЗ (рис. 2). Серия x1( o ) входит в серию x3( · ), поэтому ответ можно записать одной формулой:
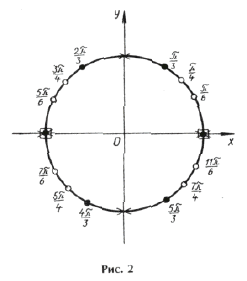
Пример 3.
sin 2x (2cos 2x cos x + cos 7x) = 0,
sin 2x (cos 3x + cos x + cos 7x) = 0,
sin 2x (cos 3x + 2cos 4x cos 3x) = 0,
sin 2x cos 3x (1 + 2cos 4x) = 0,
Объединяя все три серии корней, ответ можно записать так:
Пример 4. sin 2 x + sin 2 2x = sin 2 3x.
– (cos 2x + cos 4x) + 1 + cos 6x = 0,
– 2cos 3x cos x + 2cos2 3x = 0,
cos 3x (cos 3x – cos x) = 0,
cos 3x sin 2x sin x = 0,
Серия корней x2 содержится в серии x1 и x3, в чем легко убедиться, изобразив их различными точками на круге, поэтому
ответ:
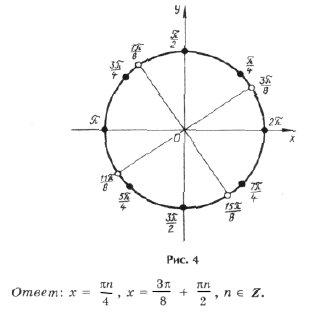
Пример 5. sin x + sin 7x – cos 5x + cos (3x – 2 p ) = 0.
2sin 4x cos 3x + 2sin 4x sin x = 0,
sin 4x (cos 3x + sin x) = 0,
Серия x2 содержится в серии корней x1, а на круге (рис. 4) изобразим точками серии x1( · ) и x3(О), которые не совпадают.
Пример 6. ctg 2x + 2ctg x – tg 2x = sin 5x.
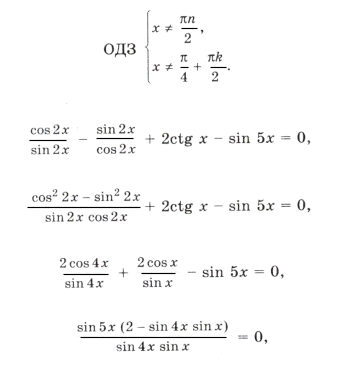
Учитывая ОДЗ, получим
Пример 7.
Иногда случается, что часть серии входит в ответ, а часть нет.
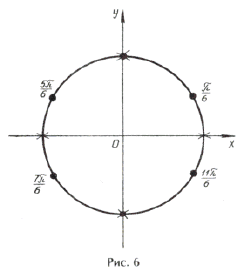
Нанесем на тригонометрический круг (рис. 6) все числа серии 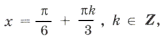
и выбросим корни, удовлетворяющие условию
Оставшиеся решения из серии x1 можно объединить в формулу
2. Отбор корней в тригонометрическом уравнении алгебраическим способом
Изображение корней на тригонометрическом круге не всегда удобно, когда период меньше 2 p .
Пример 8. sin 2 2x + sin 2 3x + sin 2 4x + sin 2 5x = 2.
cos 4x + cos 6x + cos 8x + cos 10x = 0,
2cos 5x cos x + 2cos 9x cos x = 0,
cos x cos 2x cos 7x = 0.
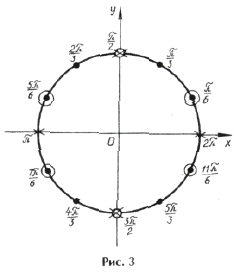
«Период» серий равен p. Рассмотрим те корни из серий x1, x2, x3, которые попадают в промежуток [0; p ]. Это будут:
Сразу видно, что серия x1 содержится в серии x3, а серии x2 и x3 не пересекаются. Значит, ответ можно записать в виде .
Способ алгебраический. Общим знаменателем в сериях x1 и x2 будет 4:
Если x1 = x2, то 2 + 4k = 1 + 2l, но слева – четное число, а справа – нечетное. Равенство невозможно, серии x1 и x2 не пересекаются. Аналогично получаем, что серии х3 и х2 тоже не пересекаются, а вот для серий x1 и x3 получаются формулы
Из равенства 7 + 14k = 1 + 2m получаем m = 7k + 3. Это означает, что для всякого k найдется целое m такое, что будет выполняться равенство 7 + 14k = 1 + 2m, т. е. всякий корень из серии x1 встретится и в серии x3, поэтому серия x1 содержится в серии x3, и в ответе писать ее не надо.
При решении некоторых тригонометрических уравнений их заменяют эквивалентной системой уравнений, а затем находят пересечение множеств решений. Эти пересечения часто найти легко. Но иногда для нахождения решений необходимо решать диафантово уравнение (ax + by = c).
Пример 9.
В данном случае сделать отбор решений на тригонометрическом круге неудобно, так как периоды серий разные. Найдем такие целые k, при которых x = p + 2 p k имеет посторонние корни, удовлетворяющие условию x № 3 p n, n О Z. Пусть p + 2 p k = 3 p n; 1 + 2k = 3n. Отсюда n = 2m + 1 Ю k = 3m + 1. Итак, посторонние корни в серии x = p + 2 p k будет при k = 3m + 1, m О Z.
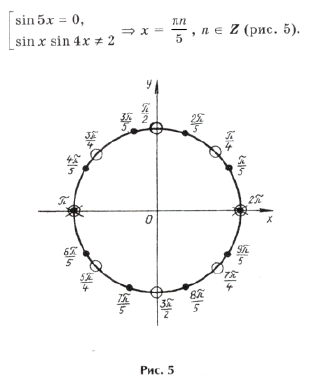
Пример 10. cos 7x (sin 5x – 1) = 0.
Пересекаются ли эти серии? Из равенства
следует 5k = 14n + 1. Выразим ту неизвестную, коэффициент при которой меньше по абсолютной величине:
– целое число.
Ответ можно записать в виде
.
Пример 11.
Поскольку наибольшее значение функции y = cos t равно 1, уравнение равносильно системе
Решением уравнения является пересечение серий x1 и x2, т. е. нам надо решить уравнение
Из него получаем уравнение, имеющее решение k = 8t, n = 3t.
Пример 12.
Решением уравнения является пересечение серий x1 и x2;
,
где
– целое число;
Пример 13.
sin 2x sin 4x = 2sin x sin 3x cos x,
sin 2x sin 4x = sin 2x sin 3x,
sin 2x (sin 4x – sin 3x) = 0,
Остается проверить, лежат ли они в области x О R,
Серию x1 проверить легко: поскольку
,
а при n, кратных 8, n = 8l (l О Z), получается как раз x № 2 p l, вся серия x1 исключается. Сложнее обстоит дело с серией x2. Здесь надо выяснить, при каких целых k найдется такое n, что выполняется равенство
,
и исключить такие k. Последнее уравнение приводится к виду 8k + 4 = 7n, причем решать это уравнение надо в целых числах. Из него следует, что n = 4l, поскольку левая часть уравнения делится на 4. Подставляя n = 4l в уравнение, получаем 8k + 4 = 28l, откуда 2k + 1 = 7l. Далее, l должно быть нечетно, l = 2t + 1; поэтому 2k + 1 = 14t + 7, k = 7t + 3. Вот решение и получилось:
Ответ:
3. Отбор корней в тригонометрическом уравнении с некоторыми условиями
Изложенные выше способы отбора корней в тригонометрических уравнениях не всегда применяются в чистом виде: выбор способа зависит от конкретных условий, но иногда эти способы комбинируются.
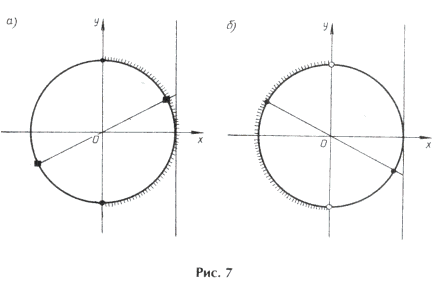
Пример 14. Найти корни уравнения sin 2x = cos x | cos x |,
удовлетворяющие условию x О [0; 2 p ].
Условию cos x і 0 удовлетворяют
из серии
из серии
Наконец,
Пример 15. Найти все решения уравнения
удовлетворяющие условию
так как
то
Пример 16. Найти все решения уравнения
принадлежащие отрезку
.
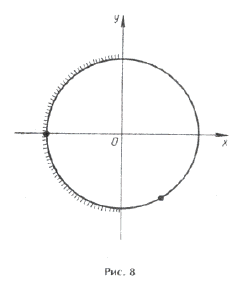
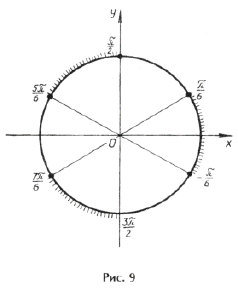
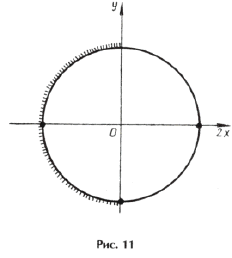
Отметим ОДЗ на тригонометрическом круге (рис. 9):
Отрезку
принадлежит только один промежуток из ОДЗ, а именно
.
Решим уравнение и выберем корни, принадлежащие этому промежутку:
1 + sin 2x = 2cos 2 3x Ю sin 2x = cos 6x,
Из серии
при n = 2 имеем
Из серии
при n = 5 имеем
Пример 17.
Ответ:
Пример 18. Найти все корни уравнения
которые удовлетворяют условию
.
10sin 2 x = – cos 2x + 3 Ю 10sin 2 x = 2sin 2 x – 1 + 3,
Выберем корни, удовлетворяющие условию задачи. Из серии
При
при
.
Аналогично выберем корни, удовлетворяющие условию задачи, из второй серии. Это будут
.
Пример 19.
sin x и cos x должны быть одинакового знака, а, учитывая первое неравенство, только при sin x > 0 и cos x > 0 система совместна. Значит, x оканчивается в первой четверти. Имеем
1 + 2sin x cos x = 4sin x cos x Ю sin 2x = 1,
Ответ:
Пример 20.
Ответ:
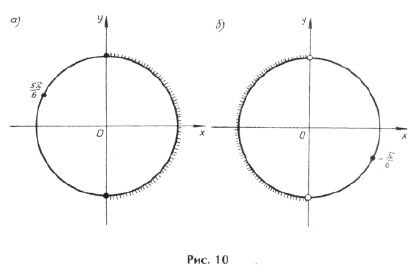
Пример 21.
а)
Но ctg x 0. Решений нет.
б)
Ответ:
.
Примеры для самостоятельного решения
7. Найти все решения уравнения, принадлежащие указанным промежуткам:

Л. Максименко,
Р. Зинченко,
г. Ангарск🔍 Видео
10 класс, 11 урок, Числовая окружностьСкачать
Трудный отбор корней из промежутка [15; 20]Скачать
Нахождение корней уравнения, принадлежащие промежуткуСкачать
ЕГЭ-ПРОФИЛЬ. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ. ЗАДАНИЕ-12Скачать
Как решать тригонометрические неравенства?Скачать
а) Решите уравнение sin2x-2sin(-x)-cos(-x)-1=0.б) Найдите все корни уравнения, принадлежащие отрезкуСкачать
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать
48 Как отобрать корни ,принадлежащие промежутку, в тригонометрическом уравненииСкачать










 Отбор корней в тригонометрических уравнениях
Отбор корней в тригонометрических уравнениях
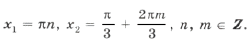
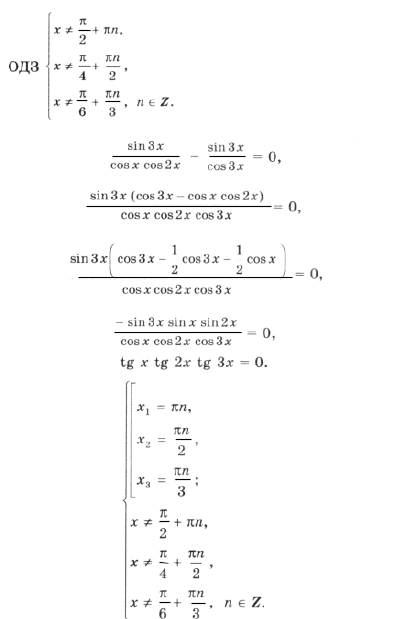
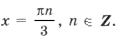
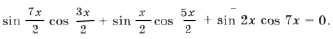
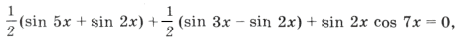
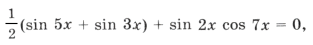
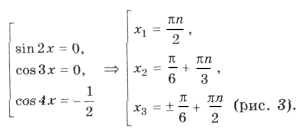
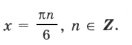
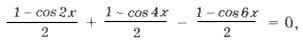
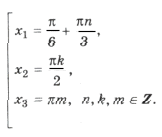
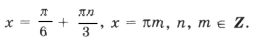
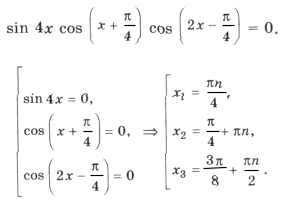
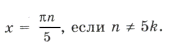
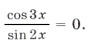
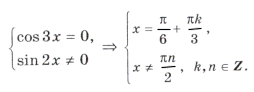
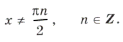
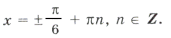
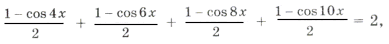
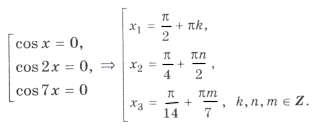
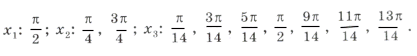
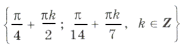
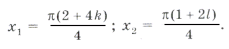
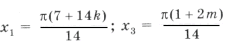
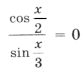
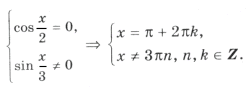
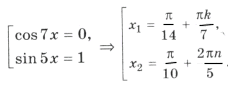
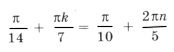
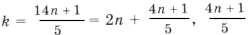 – целое число.
– целое число.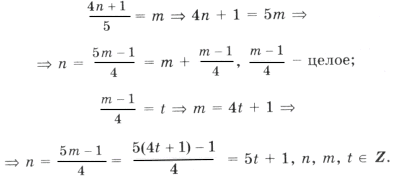
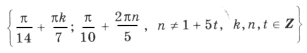 .
.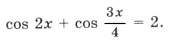
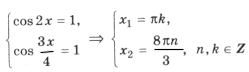
 ,
,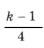 – целое число;
– целое число;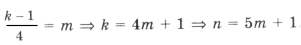
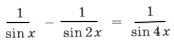
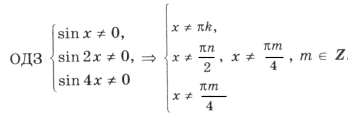
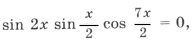
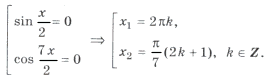
 ,
,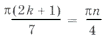 ,
,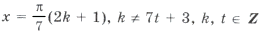
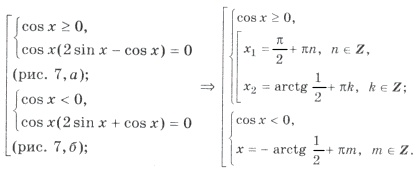

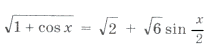
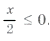
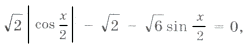
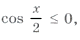 то
то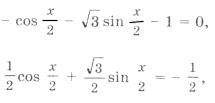
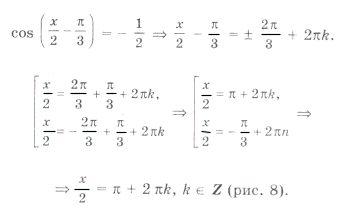
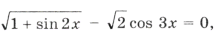
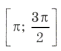 .
.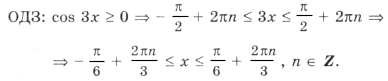
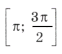 принадлежит только один промежуток из ОДЗ, а именно
принадлежит только один промежуток из ОДЗ, а именно 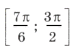 .
.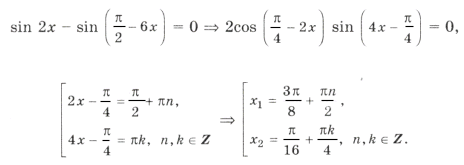
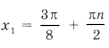 при n = 2 имеем
при n = 2 имеем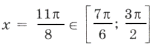
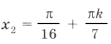 при n = 5 имеем
при n = 5 имеем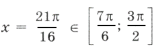
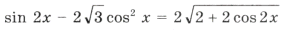
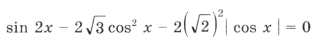
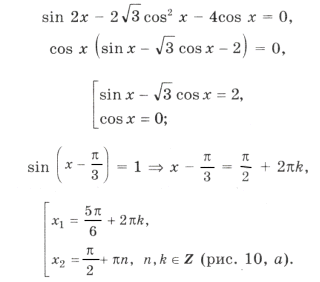
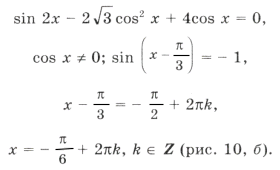
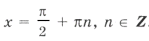
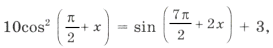
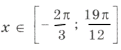 .
.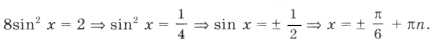
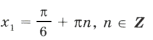
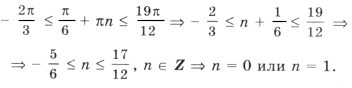
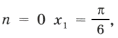
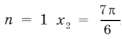 .
.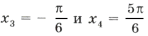 .
.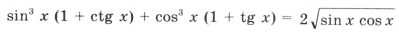
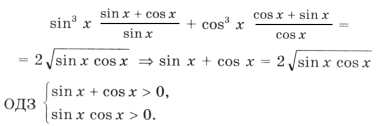
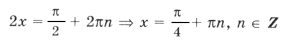
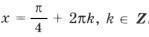
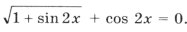
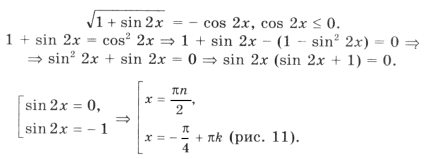
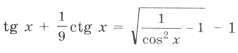
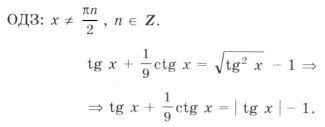
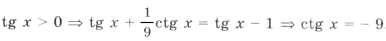
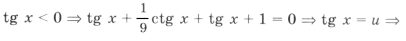
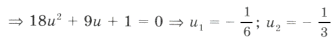
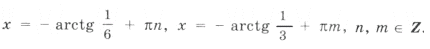
 .
.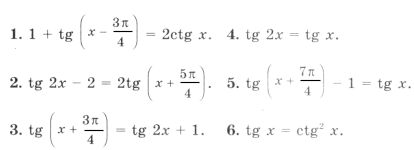
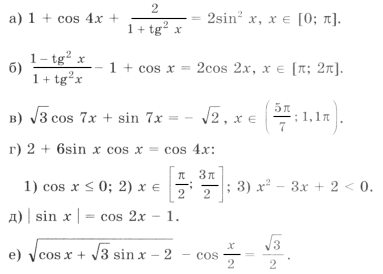


![Трудный отбор корней из промежутка [15; 20]](https://i.ytimg.com/vi/piSt0CimDxA/0.jpg)





