Равенство, содержащее неизвестную под знаком тригонометрической функции (`sin x, cos x, tg x` или `ctg x`), называется тригонометрическим уравнением, именно их формулы мы и рассмотрим дальше.
- Простейшие тригонометрические уравнения
- Формулы корней тригонометрических уравнений в таблице
- Методы решения тригонометрических уравнений
- Алгебраический метод.
- Разложение на множители.
- Приведение к однородному уравнению
- Переход к половинному углу
- Введение вспомогательного угла
- Дробно-рациональные тригонометрические уравнения
- Тригонометрические уравнения и преобразования
- Четность тригонометрических функций
- Тригонометрические тождества
- Основные тригонометрические формулы и тождества sin, cos, tg, ctg
- Основные тождества тригонометрии
- Формулы приведения
- Тригонометрические формулы сложения
- Формулы кратного угла: двойного, тройного и т.д.
- Формулы половинного угла
- Формулы понижения степени
- Сумма и разность тригонометрических функций
- Произведение тригонометрических функций
- Универсальная тригонометрическая подстановка
- 📺 Видео
Видео:Все формулы в Тригонометрии, для Чайников, Урок 6Скачать

Простейшие тригонометрические уравнения
Простейшими называются уравнения `sin x=a, cos x=a, tg x=a, ctg x=a`, где `x` — угол, который нужно найти, `a` — любое число. Запишем для каждого из них формулы корней.
1. Уравнение `sin x=a`.
При `|a|>1` не имеет решений.
При `|a| leq 1` имеет бесконечное число решений.
Формула корней: `x=(-1)^n arcsin a + pi n, n in Z`
2. Уравнение `cos x=a`
При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.
При `|a| leq 1` имеет бесконечное множество решений.
Формула корней: `x=pm arccos a + 2pi n, n in Z`
Частные случаи для синуса и косинуса в графиках.
3. Уравнение `tg x=a`
Имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arctg a + pi n, n in Z`
4. Уравнение `ctg x=a`
Также имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arcctg a + pi n, n in Z`
Видео:ФОРМУЛЫ ТРИГОНОМЕТРИИСкачать

Формулы корней тригонометрических уравнений в таблице
Для синуса:


Видео:Щелчок по математике I №5,6,12 Тригонометрия с нуля и до ЕГЭ за 4 часаСкачать

Методы решения тригонометрических уравнений
Решение любого тригонометрического уравнения состоит из двух этапов:
- с помощью тригонометрических формул преобразовать его до простейшего;
- решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.
Рассмотрим на примерах основные методы решения.
Алгебраический метод.
В этом методе делается замена переменной и ее подстановка в равенство.
Пример. Решить уравнение: `2cos^2(x+frac pi 6)-3sin(frac pi 3 — x)+1=0`
Решение. Используя формулы приведения, имеем:
`2cos^2(x+frac pi 6)-3cos(x+frac pi 6)+1=0`,
делаем замену: `cos(x+frac pi 6)=y`, тогда `2y^2-3y+1=0`,
находим корни: `y_1=1, y_2=1/2`, откуда следуют два случая:
1. `cos(x+frac pi 6)=1`, `x+frac pi 6=2pi n`, `x_1=-frac pi 6+2pi n`.
2. `cos(x+frac pi 6)=1/2`, `x+frac pi 6=pm arccos 1/2+2pi n`, `x_2=pm frac pi 3-frac pi 6+2pi n`.
Ответ: `x_1=-frac pi 6+2pi n`, `x_2=pm frac pi 3-frac pi 6+2pi n`.
Разложение на множители.
Пример. Решить уравнение: `sin x+cos x=1`.
Решение. Перенесем влево все члены равенства: `sin x+cos x-1=0`. Используя формулы двойного угла, преобразуем и разложим на множители левую часть:
`sin x — 2sin^2 x/2=0`,
`2sin x/2 cos x/2-2sin^2 x/2=0`,
`2sin x/2 (cos x/2-sin x/2)=0`,
- `sin x/2 =0`, `x/2 =pi n`, `x_1=2pi n`.
- `cos x/2-sin x/2=0`, `tg x/2=1`, `x/2=arctg 1+ pi n`, `x/2=pi/4+ pi n`, `x_2=pi/2+ 2pi n`.
Ответ: `x_1=2pi n`, `x_2=pi/2+ 2pi n`.
Приведение к однородному уравнению
Вначале нужно данное тригонометрическое уравнение привести к одному из двух видов:
`a sin x+b cos x=0` (однородное уравнение первой степени) или `a sin^2 x + b sin x cos x +c cos^2 x=0` (однородное уравнение второй степени).
Потом разделить обе части на `cos x ne 0` — для первого случая, и на `cos^2 x ne 0` — для второго. Получим уравнения относительно `tg x`: `a tg x+b=0` и `a tg^2 x + b tg x +c =0`, которые нужно решить известными способами.
Пример. Решить уравнение: `2 sin^2 x+sin x cos x — cos^2 x=1`.
Решение. Запишем правую часть, как `1=sin^2 x+cos^2 x`:
`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,
`2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0`
`sin^2 x+sin x cos x — 2 cos^2 x=0`.
Это однородное тригонометрическое уравнение второй степени, разделим его левую и правую части на `cos^2 x ne 0`, получим:
`tg^2 x+tg x — 2=0`. Введем замену `tg x=t`, в результате `t^2 + t — 2=0`. Корни этого уравнения: `t_1=-2` и `t_2=1`. Тогда:
- `tg x=-2`, `x_1=arctg (-2)+pi n`, `n in Z`
- `tg x=1`, `x=arctg 1+pi n`, `x_2=pi/4+pi n`, ` n in Z`.
Ответ. `x_1=arctg (-2)+pi n`, `n in Z`, `x_2=pi/4+pi n`, `n in Z`.
Переход к половинному углу
Пример. Решить уравнение: `11 sin x — 2 cos x = 10`.
Решение. Применим формулы двойного угла, в результате: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x/2+10 cos^2 x/2`
`4 tg^2 x/2 — 11 tg x/2 +6=0`
Применив описанный выше алгебраический метод, получим:
- `tg x/2=2`, `x_1=2 arctg 2+2pi n`, `n in Z`,
- `tg x/2=3/4`, `x_2=arctg 3/4+2pi n`, `n in Z`.
Ответ. `x_1=2 arctg 2+2pi n, n in Z`, `x_2=arctg 3/4+2pi n`, `n in Z`.
Введение вспомогательного угла
В тригонометрическом уравнении `a sin x + b cos x =c`, где a,b,c — коэффициенты, а x — переменная, разделим обе части на `sqrt `:
Коэффициенты в левой части имеют свойства синуса и косинуса, а именно сумма их квадратов равна 1 и их модули не больше 1. Обозначим их следующим образом: `frac a<sqrt >=cos varphi`, ` frac b<sqrt > =sin varphi`, `frac c<sqrt >=C`, тогда:
`cos varphi sin x + sin varphi cos x =C`.
Подробнее рассмотрим на следующем примере:
Пример. Решить уравнение: `3 sin x+4 cos x=2`.
Решение. Разделим обе части равенства на `sqrt `, получим:
`3/5 sin x+4/5 cos x=2/5`.
Обозначим `3/5 = cos varphi` , `4/5=sin varphi`. Так как `sin varphi>0`, `cos varphi>0`, то в качестве вспомогательного угла возьмем `varphi=arcsin 4/5`. Тогда наше равенство запишем в виде:
`cos varphi sin x+sin varphi cos x=2/5`
Применив формулу суммы углов для синуса, запишем наше равенство в следующем виде:
`x+varphi=(-1)^n arcsin 2/5+ pi n`, `n in Z`,
`x=(-1)^n arcsin 2/5-` `arcsin 4/5+ pi n`, `n in Z`.
Ответ. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ pi n`, `n in Z`.
Дробно-рациональные тригонометрические уравнения
Это равенства с дробями, в числителях и знаменателях которых есть тригонометрические функции.
Пример. Решить уравнение. `frac =1-cos x`.
Решение. Умножим и разделим правую часть равенства на `(1+cos x)`. В результате получим:
Учитывая, что знаменатель равным быть нулю не может, получим `1+cos x ne 0`, `cos x ne -1`, ` x ne pi+2pi n, n in Z`.
Приравняем к нулю числитель дроби: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
- `sin x=0`, `x=pi n`, `n in Z`
- `1-sin x=0`, `sin x=-1`, `x=pi /2+2pi n, n in Z`.
Учитывая, что ` x ne pi+2pi n, n in Z`, решениями будут `x=2pi n, n in Z` и `x=pi /2+2pi n`, `n in Z`.
Ответ. `x=2pi n`, `n in Z`, `x=pi /2+2pi n`, `n in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.
Видео:Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать

Тригонометрические уравнения и преобразования
Тригонометрическими уравнениями называют уравнения, в которых переменная содержится под знаком тригонометрических функций. К их числу прежде всего относятся простейшие тригонометрические уравнения, т.е. уравнения вида $sin x=a, cos x=a, tg x=a$, где $а$ – действительное число.
Перед решением уравнений разберем некоторые тригонометрические выражения и формулы.
Значения тригонометрических функций некоторых углов
| $α$ | $ 0$ | $/$ | $/$ | $/$ | $/$ | $π$ |
| $sinα$ | $ 0$ | $ /$ | $ /$ | $ /$ | $ 1$ | $ 0$ |
| $cosα$ | $ 1$ | $ /$ | $ /$ | $ /$ | $ 0$ | $ -1$ |
| $tgα$ | $ 0$ | $ /$ | $ 1$ | $ √3$ | $ -$ | $ 0$ |
| $ctgα$ | $ -$ | $ √3$ | $ 1$ | $ /$ | $ 0$ | $ -$ |
Периоды повтора значений тригонометрических функций
Период повторения у синуса и косинуса $2π$, у тангенса и котангенса $π$
Знаки тригонометрических функций по четвертям
Эта информация нам пригодится для использования формул приведения. Формулы приведения необходимы для понижения углов до значения от $0$ до $90$ градусов.
Чтобы правильно раскрыть формулы приведения необходимо помнить, что:
- если в формуле содержатся углы $180°$ и $360°$ ($π$ и $2π$), то наименование функции не изменяется; (если же в формуле содержатся углы $90°$ и $270°$ ($/$ и $/$), то наименование функции меняется на противоположную (синус на косинус, тангенс на котангенс и т. д.);
- чтобы определить знак в правой части формулы ($+$ или $-$), достаточно, считая угол $α$ острым, определить знак преобразуемого выражения.
Преобразовать $сos(90° + α)$. Прежде всего, мы замечаем, что в формуле содержится угол $90$, поэтому $cos$ измениться на $sin$.
Чтобы определить знак перед $sinα$, предположим, что угол $α$ острый, тогда угол $90° + α$ должен оканчиваться во 2-й четверти, а косинус угла, лежащего во 2-й четверти, отрицателен. Поэтому, перед $sinα$ нужен знак $-$.
$сos(90° + α)= — sinα$ — это конечный результат преобразования
Видео:✓ Тригонометрические формулы | Борис ТрушинСкачать

Четность тригонометрических функций
Косинус четная функция: $cos(-t)=cos t$
Синус, тангенс и котангенс нечетные функции: $sin(-t)= — sin t; tg(-t)= — tg t; ctg(-t)= — ctg t$
Видео:Тригонометрия. Повторяем основные формулы. Учимся их использовать. Вебинар | МатематикаСкачать

Тригонометрические тождества
- $tgα=/$
- $ctgα=/$
- $sin^2α+cos^2α=1$ (Основное тригонометрическое тождество)
Из основного тригонометрического тождества можно выразить формулы для нахождения синуса и косинуса
Вычислить $sin t$, если $cos t = / ; t ∈(/;2π)$
Найдем $sin t$ через основное тригонометрическое тождество. И определим знак, так как $t ∈(/;2π)$ -это четвертая четверть, то синус в ней имеет знак минус
Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Основные тригонометрические формулы и тождества sin, cos, tg, ctg
Основные формулы тригонометрии — это формулы, устанавливающие связи между основными тригонометрическими функциями. Синус, косинус, тангенс и котангенс связаны между собой множеством соотношений. Ниже приведем основные тригонометрические формулы, а для удобства сгруппируем их по назначению. С использованием данных формул можно решить практически любую задачу из стандартного курса тригонометрии. Сразу отметим, что ниже приведены лишь сами формулы, а не их вывод, которому будут посвящены отдельные статьи.
Видео:Тригонометрия для Чайников, 10 класс, Уравнения, Урок 7Скачать

Основные тождества тригонометрии
Тригонометрические тождества дают связь между синусом, косинусом, тангенсом и котангенсом одного угла, позволяя выразить одну функцию через другую.
sin 2 a + cos 2 a = 1 t g α = sin α cos α , c t g α = cos α sin α t g α · c t g α = 1 t g 2 α + 1 = 1 cos 2 α , c t g 2 α + 1 = 1 sin 2 α
Эти тождества напрямую вытекают из определений единичной окружности, синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg).
Видео:Как выучить все (почти все) формулы по тригонометрии? | Формулы и немного примеров | (ЧАСТЬ 1)Скачать

Формулы приведения
Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов.
sin α + 2 π z = sin α , cos α + 2 π z = cos α t g α + 2 π z = t g α , c t g α + 2 π z = c t g α sin — α + 2 π z = — sin α , cos — α + 2 π z = cos α t g — α + 2 π z = — t g α , c t g — α + 2 π z = — c t g α sin π 2 + α + 2 π z = cos α , cos π 2 + α + 2 π z = — sin α t g π 2 + α + 2 π z = — c t g α , c t g π 2 + α + 2 π z = — t g α sin π 2 — α + 2 π z = cos α , cos π 2 — α + 2 π z = sin α t g π 2 — α + 2 π z = c t g α , c t g π 2 — α + 2 π z = t g α sin π + α + 2 π z = — sin α , cos π + α + 2 π z = — cos α t g π + α + 2 π z = t g α , c t g π + α + 2 π z = c t g α sin π — α + 2 π z = sin α , cos π — α + 2 π z = — cos α t g π — α + 2 π z = — t g α , c t g π — α + 2 π z = — c t g α sin 3 π 2 + α + 2 π z = — cos α , cos 3 π 2 + α + 2 π z = sin α t g 3 π 2 + α + 2 π z = — c t g α , c t g 3 π 2 + α + 2 π z = — t g α sin 3 π 2 — α + 2 π z = — cos α , cos 3 π 2 — α + 2 π z = — sin α t g 3 π 2 — α + 2 π z = c t g α , c t g 3 π 2 — α + 2 π z = t g α
Формулы приведения являются следствием периодичности тригонометрических функций.
Видео:Формулы тригонометрии | Профильная математика ЕГЭ 2023 | УмскулСкачать

Тригонометрические формулы сложения
Формулы сложения в тригонометрии позволяют выразить тригонометрическую функцию суммы или разности углов через тригонометрические функции этих углов.
Тригонометрические формулы сложения
sin α ± β = sin α · cos β ± cos α · sin β cos α + β = cos α · cos β — sin α · sin β cos α — β = cos α · cos β + sin α · sin β t g α ± β = t g α ± t g β 1 ± t g α · t g β c t g α ± β = — 1 ± c t g α · c t g β c t g α ± c t g β
На основе формул сложения выводятся тригонометрические формулы кратного угла.
Видео:ТРИГОНОМЕТРИЯ с нуля за 30 минутСкачать

Формулы кратного угла: двойного, тройного и т.д.
sin 2 α = 2 · sin α · cos α cos 2 α = cos 2 α — sin 2 α , cos 2 α = 1 — 2 sin 2 α , cos 2 α = 2 cos 2 α — 1 t g 2 α = 2 · t g α 1 — t g 2 α с t g 2 α = с t g 2 α — 1 2 · с t g α sin 3 α = 3 sin α · cos 2 α — sin 3 α , sin 3 α = 3 sin α — 4 sin 3 α cos 3 α = cos 3 α — 3 sin 2 α · cos α , cos 3 α = — 3 cos α + 4 cos 3 α t g 3 α = 3 t g α — t g 3 α 1 — 3 t g 2 α c t g 3 α = c t g 3 α — 3 c t g α 3 c t g 2 α — 1
Видео:12 часов Тригонометрии с 0.Скачать

Формулы половинного угла
Формулы половинного угла в тригонометрии являются следствием формул двойного угла и выражают соотношения между основными функциями половинного угла и косинусом целого угла.
Формулы половинного угла
sin 2 α 2 = 1 — cos α 2 cos 2 α 2 = 1 + cos α 2 t g 2 α 2 = 1 — cos α 1 + cos α c t g 2 α 2 = 1 + cos α 1 — cos α
Видео:Формулы приведения с нуля за 15 минут!Скачать

Формулы понижения степени
sin 2 α = 1 — cos 2 α 2 cos 2 α = 1 + cos 2 α 2 sin 3 α = 3 sin α — sin 3 α 4 cos 3 α = 3 cos α + cos 3 α 4 sin 4 α = 3 — 4 cos 2 α + cos 4 α 8 cos 4 α = 3 + 4 cos 2 α + cos 4 α 8
Часто при расчетах действовать с громоздктми степенями неудобно. Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:
Общий вид формул понижения степени
sin n α = C n 2 n 2 n + 1 2 n — 1 ∑ k = 0 n 2 — 1 ( — 1 ) n 2 — k · C k n · cos ( ( n — 2 k ) α ) cos n α = C n 2 n 2 n + 1 2 n — 1 ∑ k = 0 n 2 — 1 C k n · cos ( ( n — 2 k ) α )
sin n α = 1 2 n — 1 ∑ k = 0 n — 1 2 ( — 1 ) n — 1 2 — k · C k n · sin ( ( n — 2 k ) α ) cos n α = 1 2 n — 1 ∑ k = 0 n — 1 2 C k n · cos ( ( n — 2 k ) α )
Видео:Основное тригонометрическое тождество. 9 класс.Скачать
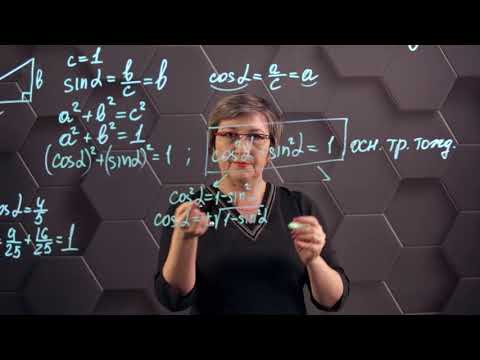
Сумма и разность тригонометрических функций
Разность и сумму тригонометрических функций можно представить в виде произведения. Разложение на множители разностей синусов и косинусов очень удобно применять при решении тригонометрических уравнений и упрощении выражений.
Сумма и разность тригонометрических функций
sin α + sin β = 2 sin α + β 2 · cos α — β 2 sin α — sin β = 2 sin α — β 2 · cos α + β 2 cos α + cos β = 2 cos α + β 2 · cos α — β 2 cos α — cos β = — 2 sin α + β 2 · sin α — β 2 , cos α — cos β = 2 sin α + β 2 · sin β — α 2
Видео:18+ Математика без Ху!ни. Формулы ПриведенияСкачать

Произведение тригонометрических функций
Если формулы суммы и разности функций позволяют перейти к их произведению, то формулы произведения тригонометрических функций осуществляют обратный переход — от произведения к сумме. Рассматриваются формулы произведения синусов, косинусов и синуса на косинус.
Формулы произведения тригонометрических функций
sin α · sin β = 1 2 · ( cos ( α — β ) — cos ( α + β ) ) cos α · cos β = 1 2 · ( cos ( α — β ) + cos ( α + β ) ) sin α · cos β = 1 2 · ( sin ( α — β ) + sin ( α + β ) )
Видео:Формулы приведения - как их легко выучить!Скачать

Универсальная тригонометрическая подстановка
Все основные тригонометрические функции — синус, косинус, тангенс и котангенс, — могут быть выражены через тангенс половинного угла.
Универсальная тригонометрическая подстановка
sin α = 2 t g α 2 1 + t g 2 α 2 cos α = 1 — t g 2 α 2 1 + t g 2 α 2 t g α = 2 t g α 2 1 — t g 2 α 2 c t g α = 1 — t g 2 α 2 2 t g α 2
📺 Видео
Вся Тригонометрия для Чайников, 10 класс, урок 1Скачать

Вся тригонометрия к ЕГЭ за 20 минут | Математика ЕГЭ — Эрик ЛегионСкачать

Тригонометрическая окружность. Как выучить?Скачать

Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать






