Все фигуры и их уравнения

Уравнение фигуры — это уравнение с двумя переменными x и y, для которого выполняются два условия: 1) координаты любой точки фигуры F удовлетворяют этому уравнению.

Содержание:

Понятие уравнения фигур

Название этого раздела означает: геометрические фигуры можно задавать уравнениями (некоторые фигуры можно задавать неравенствами).

Известно, что точки плоскости и пространства задаются их координатами, геометрические фигуры могут задаваться уравнениями или неравенствами: — уравнение прямой; — уравнение окружности; — уравнение сферы и т. д.

Говорят, что фигура F задается уравнением в прямоугольных координатах, если точка принадлежит фигуре F тогда и только тогда, когда координаты этой точки удовлетворяют данному уравнению. Это означает, что выполняются два условия:

1. Если точка принадлежит фигуре F, то ее координаты удовлетворяют данному уравнению.

2. Если числа х, у, г удовлетворяют данному уравнению, то точка с такими координатами принадлежит фигуре F.

Второе условие можно выразить иначе: координаты любой точки, не принадлежащей фигуре F, не удовлетворяют данному уравнению.

Например, прямая, перпендикулярная оси Ох и проходящая через точку М(2, 0), на оси Ох задается уравнением х = 2 (рис. 2.461). Действительно, каждая точка, лежащая на этой прямой, имеет одну и ту же координату 2. А любая точка, не лежащая на этой прямой, имеет другое значение координаты х, нежели 2. Ось Оу задается уравнением х = 0.

Аналогично прямая, перпендикулярная оси Оу и проходящая через точку Щ0, 3), имеет уравнение у = 3 (рис. 2.462). Ось Ох имеет уравнение у = 0.

Уравнение прямой

Можно доказать такую теорему.

Теорема 3. Любая прямая в декартовой системе координат хОу имеет уравнение вида — некоторые числа.

Выясним, как расположена прямая относительно осей координат, если ее уравнение имеет тот или иной частный вид.

1. В этом случае уравнение прямой можно переписать так:

Таким образом, все точки прямой имеют одну и ту же ординату ; следовательно, прямая параллельна оси х (рис. 2.463). В частности, если с = 0, то прямая совпадает с осью Ох.

2. Этот случай рассматривается аналогично. Прямая параллельна оси Оу (рис. 2.464) и совпадает с ней, если и с = 0.

3. с = 0. Прямая проходит через начало координат, так как его координаты (0; 0) удовлетворяют уравнению прямой (рис. 2.465).

Если в общем уравнении прямой коэффициент при у не равен нулю, то это уравнение можно разрешить относительно у. Получим: Или, обозначая получим: у = kх + d.

Коэффициент k в уравнении прямой с точностью до знака равен тангенсу острого угла, который образует прямая с осью Ох. В уравнении прямой, изображенной на рисунке 2.466, k > 0.

Коэффициент k в уравнении прямой называют угловым коэффициентом прямой.

Уравнения окружности и сферы

Составим уравнение окружности с центром в точке и радиусом R (рис. 2.467).

1. Возьмем произвольную точку А(х, у) на окружности. Расстояние от нее до центра О равно R.

2. Квадрат расстояния от точки А до точки О равен (формула расстояния между точками).

3. Координаты х, у каждой точки А окружности удовлетворяют уравнению

(2, определение окружности).

Получили искомое уравнение. Обратно: любая точка А, координаты которой удовлетворяют уравнению окружности, принадлежит окружности, так как расстояние от нее до точки О равно R. Отсюда следует, что данное уравнение действительно является уравнением окружности с центром в точке О и радиусом R.

Заметим, что если центром окружности является начало координат, то уравнение окружности имеет вид:

Выведем теперь уравнение сферы. Пусть в пространстве введена прямоугольная система координат и задана сфера S с центром и радиусом R. Эта сфера есть множество точек М, для которых расстояние от А равно R, т. е. AM = R (рис. 2.468).

Пусть х, у, z — координаты точки М. Согласно формуле расстояния между точками в пространстве, предыдущее равенство можно записывать в координатах так:

Это и есть уравнение сферы S с центром и радиусом R, т. е. множество точек, координаты которых удовлетворяют данному уравнению, представляет собой сферу S (рис. 2.468).

Если центр А находится в начале координат, т. е. то уравнение получает простой вид:

Рассмотрим шар с центром и радиусом R (рис. 2.469).

По определению, это множество точек М, для которых , т. е. . Выражая расстояние AM через координаты точки М(х, у, z), получим:

Это неравенство задает шар S с центром и радиусом R, так как оно равносильно неравенству , задающему такой шар по самому его определению.

Если центр шара находится в начале координат, то уравнение шара упрощается и имеет вид:

Два предприятия A и В производят продукцию с одной и той же ценой т за одно изделие. Однако автопарк, обслуживающий предприятие А, оснащен более современными и более мощными грузовыми автомобилями. В результате транспортные расходы на перевозку одного изделия составляют для предприятия А 10 руб. на 1 км, а для предприятия В 20 руб. на 1 км. Расстояние между предприятиями 300 км. Как территориально должен быть разделен рынок сбыта между двумя предприятиями для того, чтобы расходы потребителей при покупке изделий были минимальными?

Решение:

1. Выберем систему координат так, чтобы ось Ох проходила через пункты А и В, а ось Оу — через точку А (построение) (рис. 2.470).

2. Пусть N — произвольная точка, — расстояния от точки N до предприятий А и Б (рис. 2.471).

3. При доставке груза из пункта А расходы равны (1,2).

4. При доставке груза из пункта Б расходы равны (1,2).

5. Если для пункта N выгоднее доставлять груз с предприятия А, то откуда , в обратном случае получим (3,4).

6. Таким образом, границей этих двух областей для каждой точки, до которой расходы на перевозку груза из пунктов А и Б равны, будет множество точек плоскости, удовлетворяющих уравнению (5)

7. Выразим через координаты:

(1,2, формула расстояния между точками).

8. Имея в виду равенство из п. 6, получим:

(6,7).

9. Это есть уравнение окружности (рис. 2.472).

Следовательно, для всех пунктов, попадающих во внутреннюю область круга, выгоднее привозить груз из пункта В, а для всех пунктов, попадающих во внешнюю часть круга, — из пункта А.

Пример 2.

Два наблюдаемых пункта находятся в точках Пункт наблюдения О находится на прямой АВ и удален от точки А на расстояние км, а от В на расстояние с км (с > ). Наблюдатель для безопасности должен идти по такому пути, чтобы расстояние от него до пункта А все время оставалось в два раза больше, чем расстояние от него до пункта В. По какой линии должен идти наблюдатель?

Решение:

Из условий задачи имеем:

1. Два наблюдаемых пункта находятся в точках

2. Пункт наблюдения О находится на прямой АВ и удален от А на расстоянии км, а от В — с км (с > ).

3. Наблюдатель идет так, чтобы расстояние до пункта А было в два раза больше, чем до В.

4. По какой линии должен идти наблюдатель?

5. Примем за начало координат наблюдательный пункт О и направление оси Ох будет проходить через пункты А и В (по условию задачи эти три точки находятся на одной прямой) (рис. 2.473).

6. Пусть наблюдатель находится в точке М(х, у). Вычислим расстояние от наблюдателя до пунктов А и В (рис. 2.473):

(1, 2, 3, 5, формула расстояния между точками).

7. По условию задачи имеем: МА = 2MB, т. е.

(3, 6).

8. Решая это уравнение, получим:

9. Раскроем скобки и перегруппируем:

10. Наблюдатель должен идти по окружности с центром и радиусом (4, уравнение окружности).

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

Смотрите также дополнительные лекции по предмету «Математика»:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Плоские геометрические фигуры: свойства и основные формулы

В статье описываются геометрические фигуры: определение, основные свойства и формулы.

Плоские геометрические фигуры:

Четырехугольник (общее для всех четырехугольников)

Квадрат

Прямоугольник

Параллелограмм

Трапеция

Треугольник

Окружность

Геометрические фигуры — это любое сочетание точек, линий и поверхностей. Геометрические фигуры разделяются на плоские и объемные.

Плоские геометрические фигуры — это фигуры, все точки которых лежат на одной плоскости. Объемные геометрические фигуры — это фигуры, не все точки которых лежат на одной плоскости.

Видео:Основные геометрические фигуры и их параметры. Вебинар | МатематикаСкачать

Четырёхугольник

Четырёхугольник – это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три точки не лежат на одной прямой.

Основные свойства:

• Сумма углов четырёхугольника равна 360°
• Не существует четырёхугольников, у которых все углы острые или все углы тупые.
• Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов.
• Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон.

В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны. Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.

Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°.Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.

Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Квадрат

Квадрат – правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.

Основные формулы:

Периметр: P=4a, где P-периметр, a-сторона
Площадь: S=a 2 или S=d 2 /2
Сторона и диагональ связаны соотношениями: a=d/√2, d=a√2
Радиус описанной окружности: R=d или R=a/√(2)
Радиус вписанной окружности: r=a/2

где a-сторона, d-диагональ, P-периметр, S-площадь
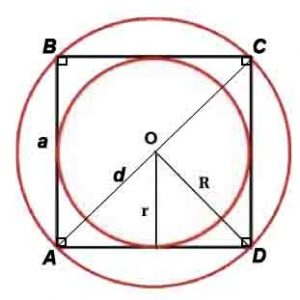
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(2) – корень квадратный из 2.

Свойства:

• Все стороны равны, все углы равны и составляют 90°;
• Диагонали квадрата равны и перпендикулярны;
• У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей;
• Квадрат является одновременно частным случаем ромба и прямоугольника.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Прямоугольник

Прямоугольник – четырехугольник, у которого все углы прямые.

Основные формулы:

Периметр: P=(a+b)*2
Площадь по сторонам: S = a*b
Площадь по диагонали и углу между ними: S = d²* sin γ. / 2
Стороны и диагональ связаны соотношением: d=√(a 2 +b 2 )/2 (теорема Пифагора)
Радиус описанной окружности: R= √(a 2 +b 2 )/2 (теорема Пифагора)

где a, b – длины сторон прямоугольника, d-диагональ, P-периметр, S-площадь
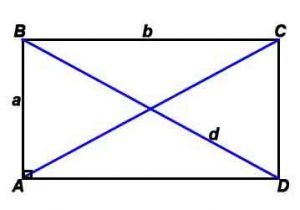
γ – угол между диагоналями
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(a 2 +b 2 ) – корень квадратный из (a 2 +b 2 ).

Свойства:

• Диагонали прямоугольника равны и делятся точкой пересечения пополам.
• Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали.

Видео:Уравнение окружности (1)Скачать

Параллелограмм

Параллелограмм – четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.

Определения:

Высота параллелограмма – это перпендикуляр, проведённый из вершины параллелограмма к противоположной стороне.

Основные формулы:

Стороны и диагональ связаны соотношением: (d₁) 2 +(d₂) 2 =(a 2 +b 2 )*2
Периметр: P=(a+b)*2
Площадь по стороне и высоте: S = a*h
S (Площадь) по двум сторонам и углу между ними: S=a*b*sin α
S (Площадь) по двум диагоналям и углу между ними: S=(d₁*d₂)/2*sin γ

где a, b – длины сторон, d₁, d₂ –диагонали, P-периметр, S-площадь,
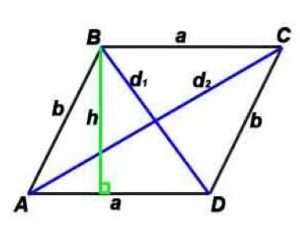
h-высота, проведенная к противоположной стороне
α – угол между сторонами параллелограмма,
γ – угол между диагоналями параллелограмма (острый).

Свойства:

• У параллелограмма противоположные стороны равны и противоположные углы равны.
• Сумма любых двух соседних углов параллелограмма равна 180°.
• Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
• Каждая диагональ делит параллелограмм на два равных треугольника.
• Две диагонали параллелограмма делят его на четыре равновеликих треугольника (равны площади всех 4-х треугольников)
• Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
• Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.

Видео:Повторяем решение уравнений. Полезно всем! Вебинар | МатематикаСкачать

Ромб

Ромб – это параллелограмм, у которого все стороны равны.

Основные формулы:

Периметр: P=4*a
Площадь по стороне и высоте: S=a*h
Площадь по диагоналям: S = (d₁*d₂)/2
Радиус окружности, вписанной в ромб: r=h/2 или r =(d₁*d₂)/4a
Площадь по стороне и радиусу вписанной окружности: S=2*a*r
Площадь по стороне и углу: S = a 2 · sin α

где a – длина стороны, d₁, d₂ –диагонали, P-периметр, S-площадь,
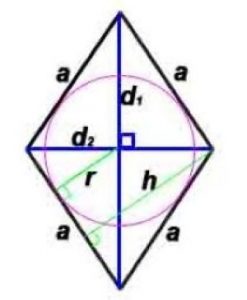
h -высота, проведенная к противоположной стороне
α – угол между сторонами ромба

Свойства:

• Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.
• В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей. Радиус окружности: r=h/2 или r = d₁*d₂/4a.

Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Трапеция

Трапеция – четырёхугольник, у которого только две противолежащие стороны параллельны.

Определения:

• Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.
• Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.
• Средняя линия (первая средняя линия) трапеции – отрезок, который соединяет середины боковых сторон данной трапеции.Средняя линия трапеции параллельна её основаниям и равна их полусумме.
• Средняя линия (вторая средняя линия) – отрезок, соединяющий середины оснований, проходит через точку пересечения диагоналей.
• Равнобокая трапеция – трапеция,у которой боковые стороны равны (c=d). У равнобокой трапеции:диагонали равны, углы при основании равны, сумма противолежащих углов равна 180°.Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая.
• Прямоугольная трапеция – трапеция, у которой одна из её боковых сторон перпендикулярна основаниям.

Основные формулы:

Периметр: P=a+b+c+d
Площадь определить: S=h*(a+b)/2
Стороны и диагональ равнобокой трапеции: d² = ab+c²
Радиус вписанной окружности: r = h/2

где a,b – основания, c,d – боковые стороны (с – боковые стороны в случае, если трапеция равнобокая), d₁, d₂ –диагонали,
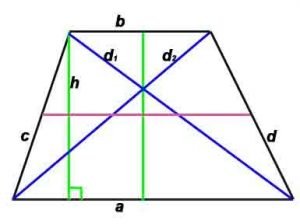
P-периметр, S-площадь, h -высота, проведенная к противоположной стороне

Свойства:

В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон (a+b=c+d). Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.

Видео:Математика это не ИсламСкачать

Треугольник

Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).

Определения:

• Углами (внутренними углами) треугольника называются три угла, каждый из которых образован лучами, выходящими из вершин треугольника и проходящими через две другие вершины.
• Высота треугольника – перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны
• Медиана треугольника– отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
• Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне
• Равные треугольники – треугольники, у которых соответствующие стороны равны и соответствующие углы равны
• Равнобедренный треугольник– треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
• Равносторонний или правильный треугольник – треугольник, у которого все стороны равны.
• Прямоугольный треугольник – треугольник, у которого есть прямой угол. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.

Основные формулы:

Периметр: P=a+b+c
Площадь по стороне и высоте: S=(a*h)/2
Площадь: по сторонам и углу между ними: S=(a*b)/2* sin γ
по трем сторонам и радиусу описанной окружности: S=(a*b*c)/4R
по трем сторонам и радиусу вписанной окружности: S=(a+b+c)/2*r
Площадь прямоугольного треугольника: S=(a*b)/2
Стороны прямоугольного треугольника: c 2 =a 2 +b 2 (Теорема Пифагора)

где a,b, c – стороны (a,b –катеты , с – гипотенуза в случае прямоугольного треугольника)
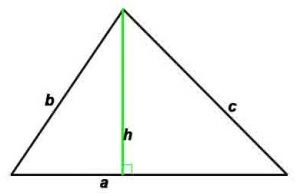
d₁, d₂ –диагонали, h -высота, проведенная к противоположной стороне,
P-периметр, S-площадь, γ – угол между сторонами a и b
r – радиус вписанной окружности, R – радиус описанной окружности

Свойства:

• В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.
• Сумма углов треугольника равна 180°:
• Длина каждой стороны треугольника больше разности и меньше суммы длин двух других сторон: |a-b| 2 =a 2 +b 2 (Теорема Пифагора).В прямоугольном треугольнике гипотенуза всегда больше любого из катетов.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Окружность

Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра окружности), которая лежит в той же плоскости, что и кривая.

Определения:

• Радиус – отрезок, который соединяет центр окружности с любой её точкой.
• Хорда – отрезок, который соединяет какие-либо две точки окружности (AB).
• Диаметр – хорда, проходящая через центр окружности(d). Диаметр – наибольшая хорда окружности. Наименьшей хорды окружности не существует.
• Касательная – прямая, которая лежит в одной плоскости с окружностью и имеет с ней только одну общую точку (E)
• Секущая – прямая, которая пересекает окружность в двух различных точках.

Основные формулы:

Длина окружности: L = 2πR
Площадь круга: S = π*r 2 или S = π*d 2 /4

где π = 3,14 (3,1415926535) – величина постоянная,
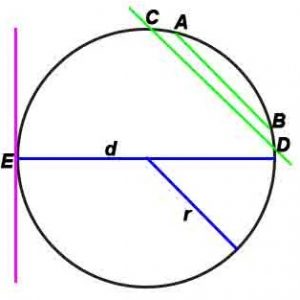
где r-радиус, d –диаметр, L – длина окружности, S-площадь.

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Кривые второго порядка — определение и построение с примерами решения

Содержание:

Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру — значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде

1. Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
2. если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.

Это определение в более компактной записи выглядит следующим образом. Уравнение называется уравнением фигуры, если , то есть (а, b) — решение уравнения F(x,y) = 0.

Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения , т.е. уравнение фигуры задает эту фигуру.

Возможны два вида задач:

1. дано уравнение и надо построить фигуру Ф, уравнением которой является ;
2. дана фигура Ф и надо найти уравнение этой фигуры.

Первая задача сводится к построению графика уравнения и решается, чаще всего, методами математического анализа.

Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:

1. Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
2. Записать в координатах условие, сформулированное в первом пункте.

Видео:Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

Эллипс

Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек , есть величина постоянная (большая, чем расстояние между ).

Точки называются фокусами эллипса. Обозначив расстояние между фокусами через 2с, а сумму расстояний от точек эллипса до фокусов через 2а, имеем с b. В этом случае а называется большой полуосью, a b — малой.

Если а =Ь, то уравнение (7.3) можно переписать в виде:

(7.5)

Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку координаты которой задаются формулами будет окружность (4) переводить в эллипс, заданный соотношением

Число называется эксцентриситетом эллипса. Эксцентриситет характеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличении становится более вытянутым

Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами . Их длины и задаются формулами Прямые называются директрисами эллипса. Директриса называется левой, а — правой. Так как для эллипса и, следовательно, левая директриса располагается левее левой вершины эллипса, а правая — правее правой вершины.

Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Гипербола

Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек есть величина постоянная (не равная нулю и меньшая, чем расстояние между ).

Точки называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно 2с. Модуль расстояний от точек гиперболы до фокусов обозначим через а. По условию, а 0) (рис. 9.7). Ось абсцисс проведём через фокус F перпендикулярно директрисе. Начало координат расположим посередине между фокусом и директрисой. Пусть А — произвольная точка плоскости с координатами (х, у) и пусть . Тогда точка А будет лежать на параболе, если r=d, где d- расстояние от точки А до директрисы. Фокус F имеет координаты .

Тогда А расстояние Подставив в формулу r=d, будем иметь. Возведя обе части равенства в квадрат, получим

или

(9.4.1)

Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения также определяют параболы.

Легко показать, что уравнение , определяет параболу, ось симметрии которой перпендикулярна оси абсцисс; эта парабола будет восходящей, если а > 0 и нисходящей, если а О. Для этого выделим полный квадрат:

и сделаем параллельный перенос по формулам

В новых координатах преобразуемое уравнение примет вид: где р — положительное число, определяется равенством .

Пример:

Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию, называется параболой. Прямая у = -1 называется директрисой параболы, а точка F — фокусом параболы. Чтобы выяснить, как располагаются точки Р, удовлетворяющие условию, запишем это равенство с помощью координат: , или после упрощения . Это уравнение геометрического места точек, образующих параболу (рис. 9.8).

Видео:Простейшие геометрические фигуры и их свойстваСкачать

Кривые второго порядка на плоскости

Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:

где коэффициенты А, В и С не равны одновременно нулю

Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.

Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.

Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению

которое называют каноническим уравнением эллипса.

Число а называют большей полуосью эллипса, число — мень-

шей полуосью эллипса, 2а и 2b — соответственно большей и меньшей осями эллипса. Точки называют вершинами эллипса, а — его фокусами (рис. 12).

Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии. Центр симметрии эллипса называется центром эллипса.

Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.

В случае а=b каноническое уравнение эллипса принимает вид и определяет окружность радиуса а с центром в начале координат.

Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.

Так, в случае а>b эксцентриситет эллипса выражается формулой:

Эксцентриситет изменяется от нуля до единицы и характеризует форму эллипса. Для окружности Чем больше эксцентриситет, тем более вытянут эллипс.

Пример:

Показать, что уравнение

является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.

Решение:

Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:

— каноническое уравнение эллипса с центром в точке большей полуосью а=3 и меньшей полуосью

Найдем эксцентриситет эллипса:

Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке а оси параллельны соответственно осям Ох, Оу и имеют те же направления (осуществили преобразование параллельного переноса). Тогда новые координаты точки будут равны ее старым координатам минус старые координаты нового начала, т.е.

В новой системе координат координаты вершин и фокусов гиперболы будут следующими:

Переходя к старым координатам, получим:

Построим график эллипса.

Задача решена.

Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.

Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

🎥 Видео

Всё про углы в окружности. Геометрия | МатематикаСкачать

УРАВНЕНИЕ ОКРУЖНОСТИСкачать

9 класс, 6 урок, Уравнение окружностиСкачать

ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Уравнение, которое меняет взгляд на мир [Veritasium]Скачать

Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать