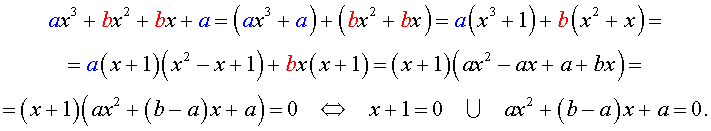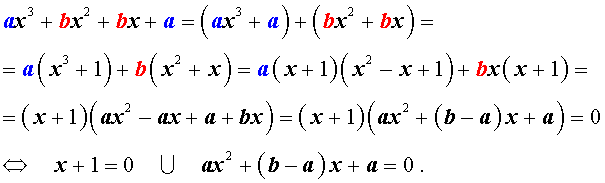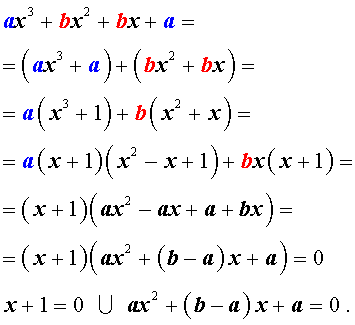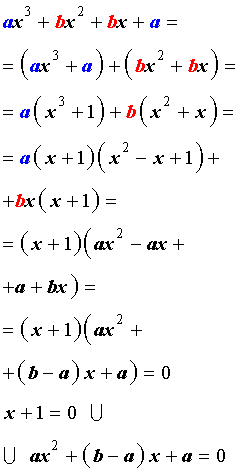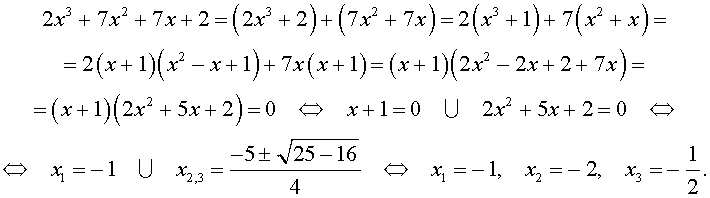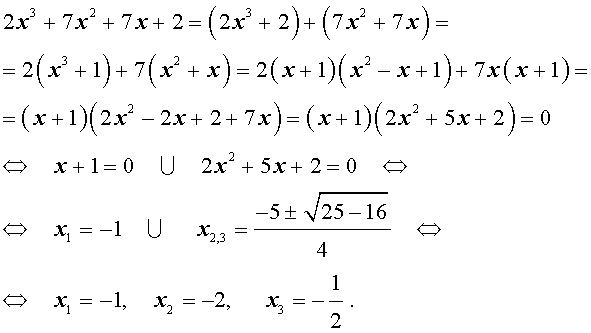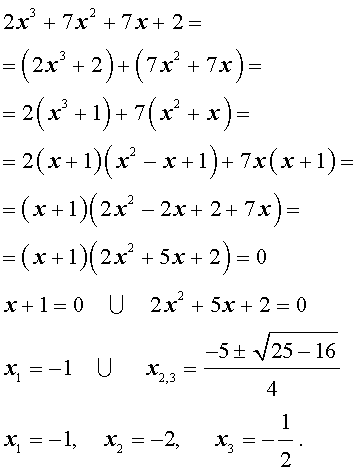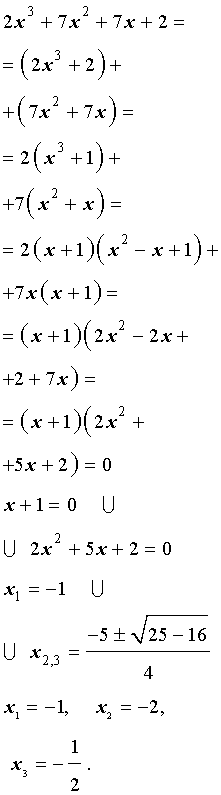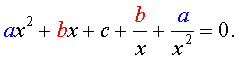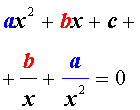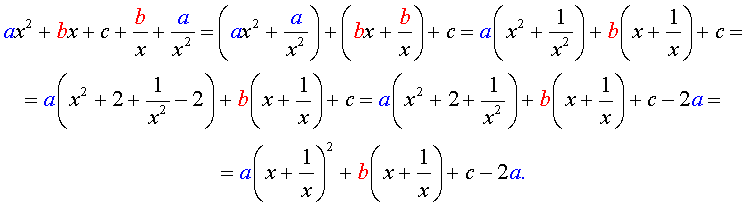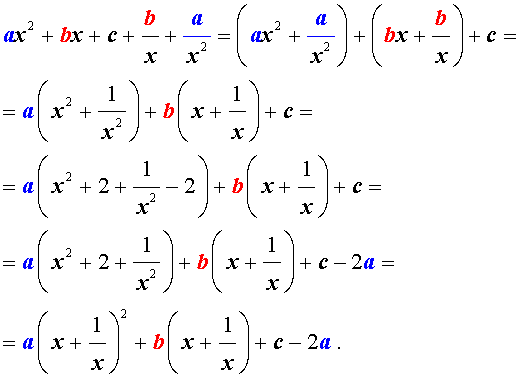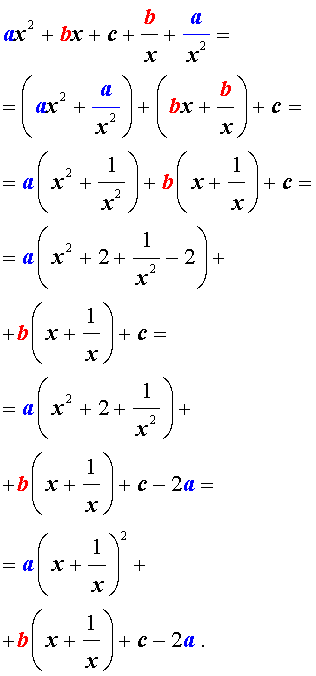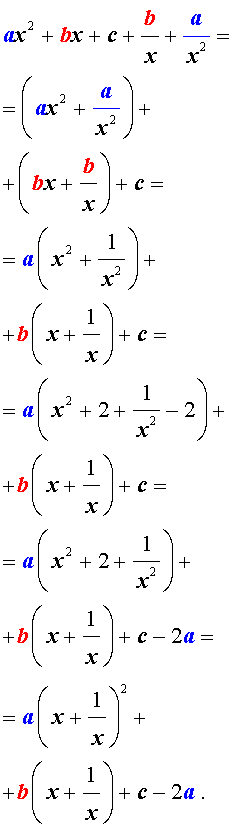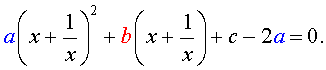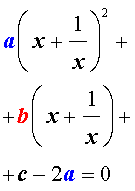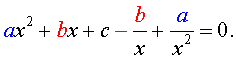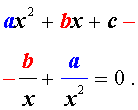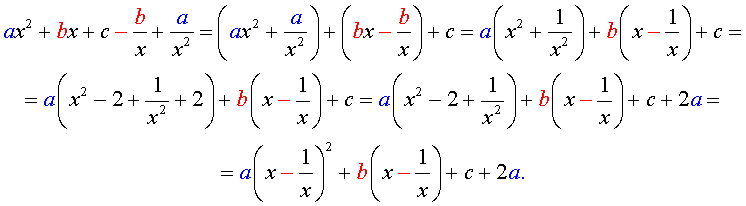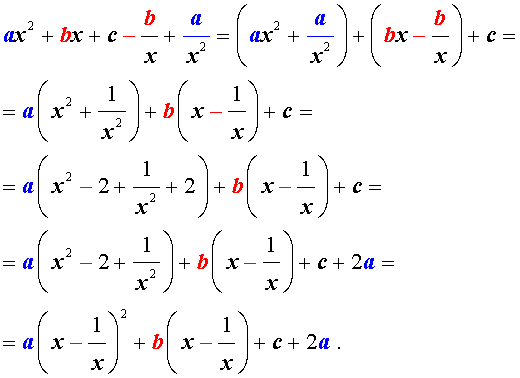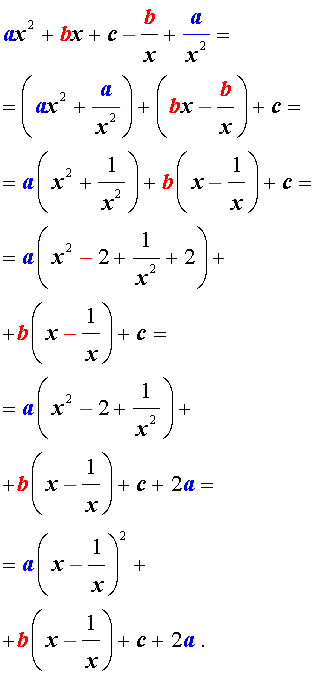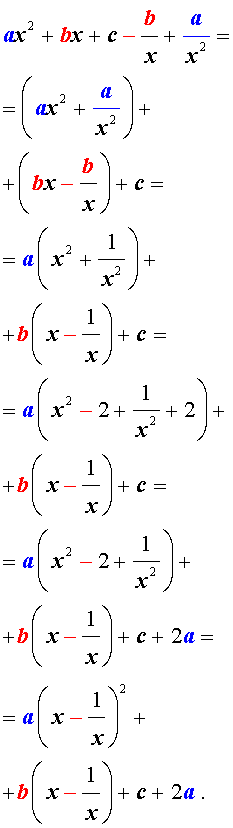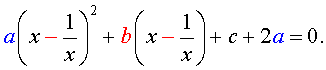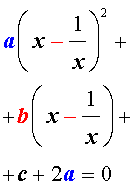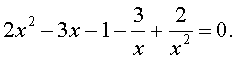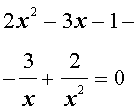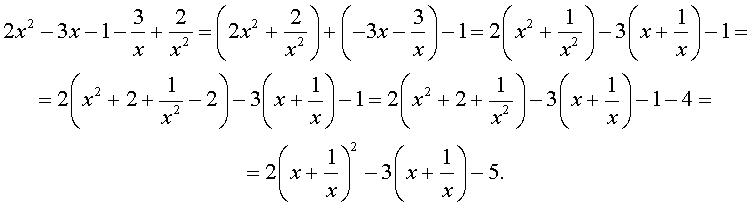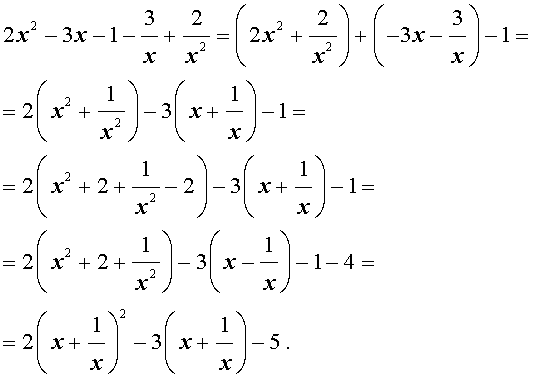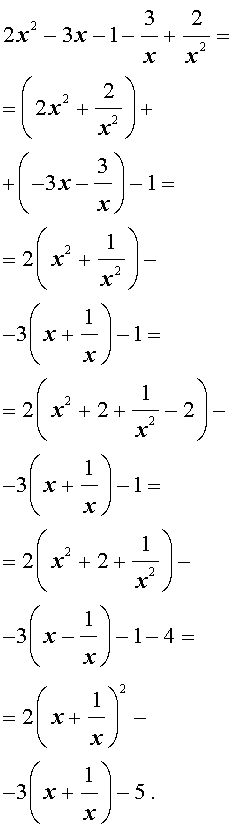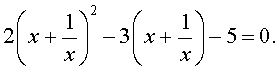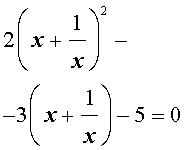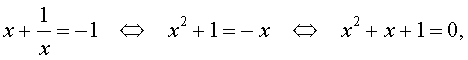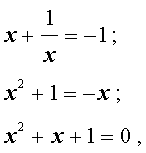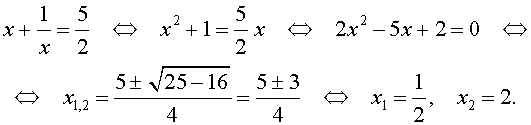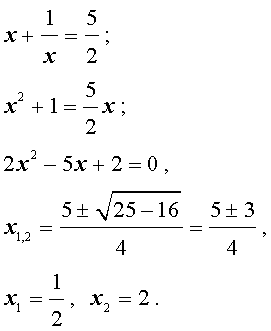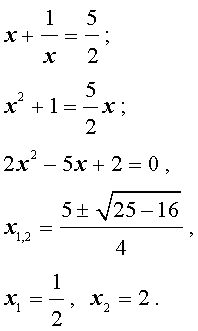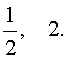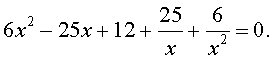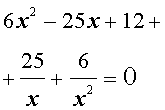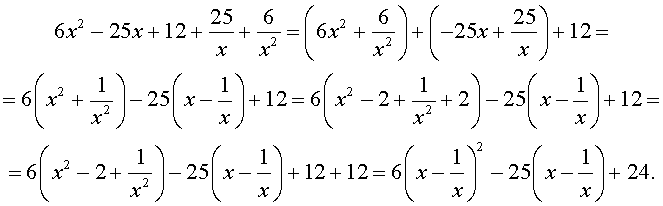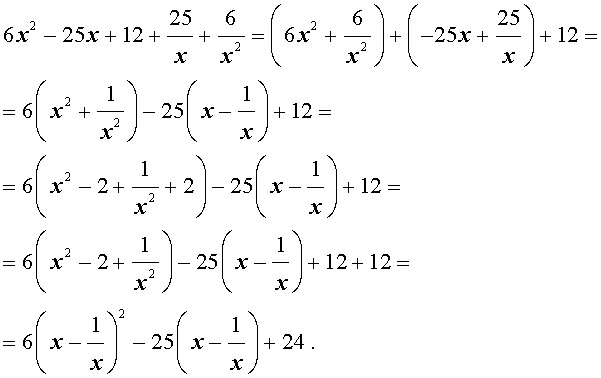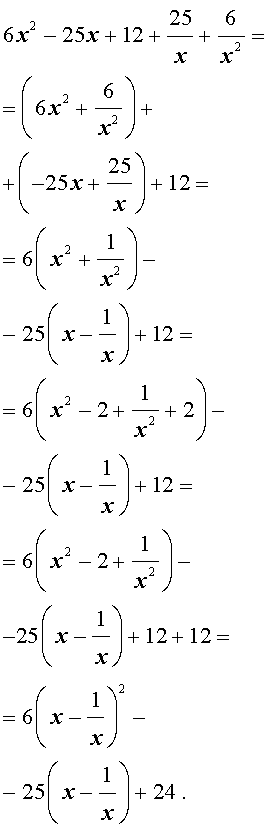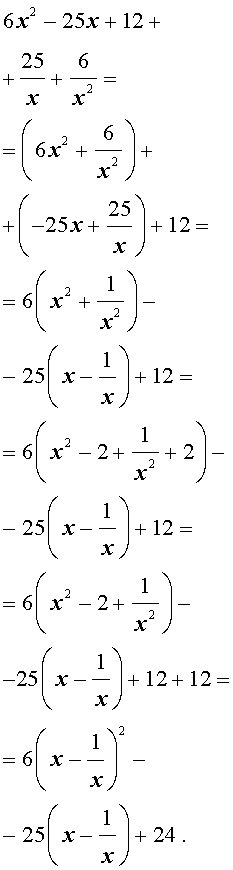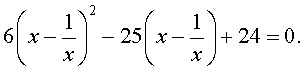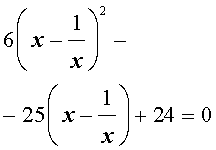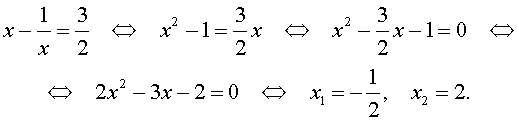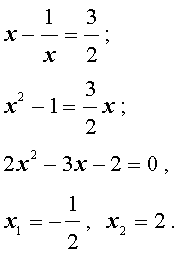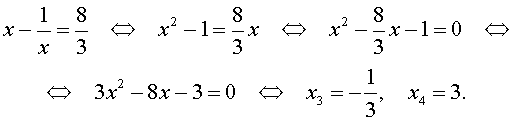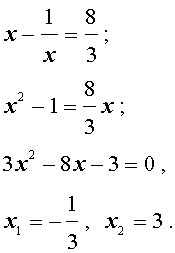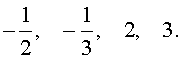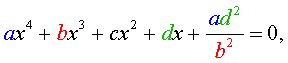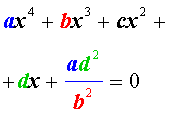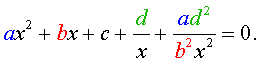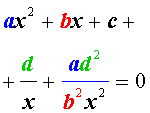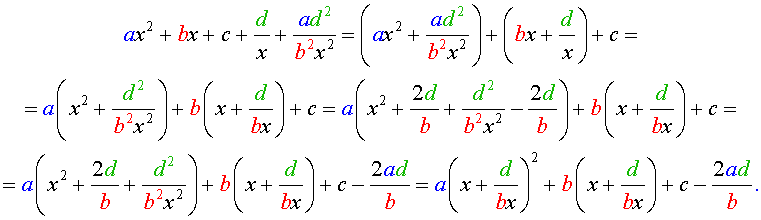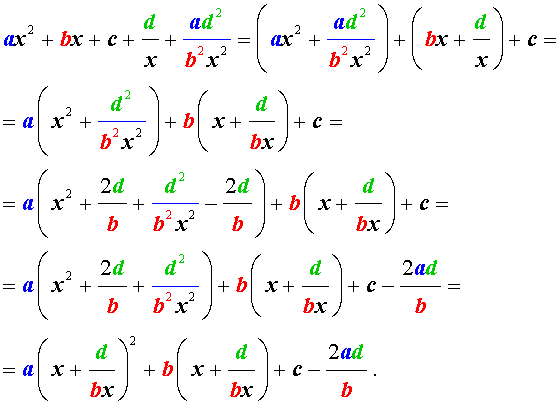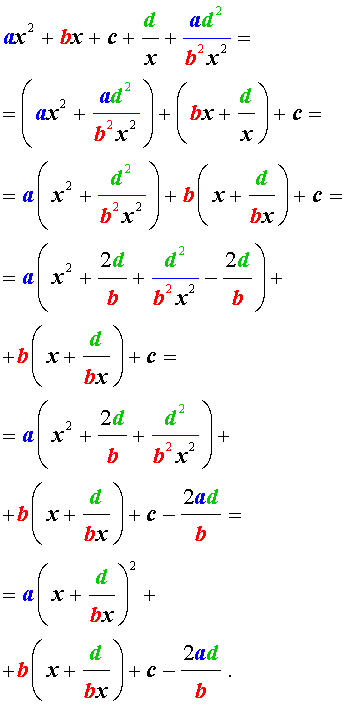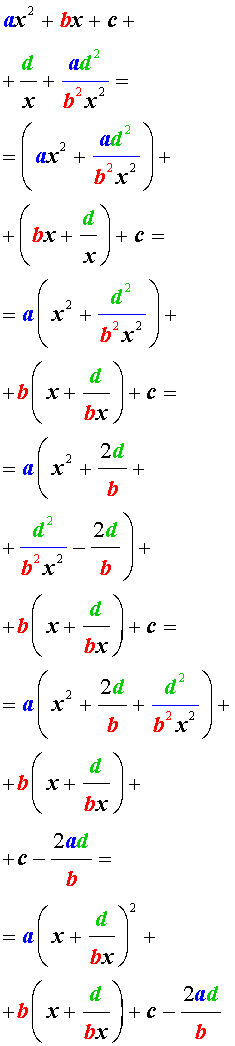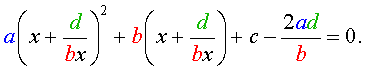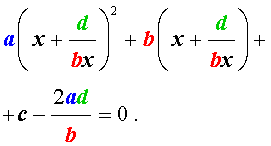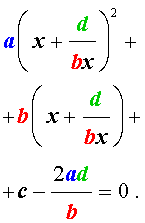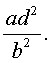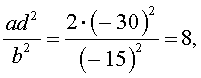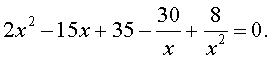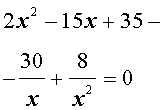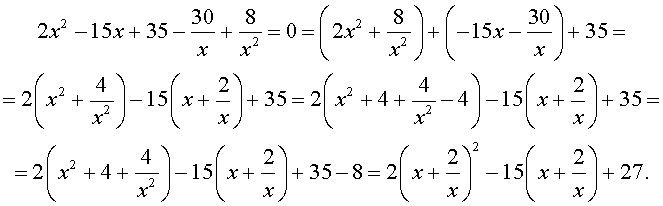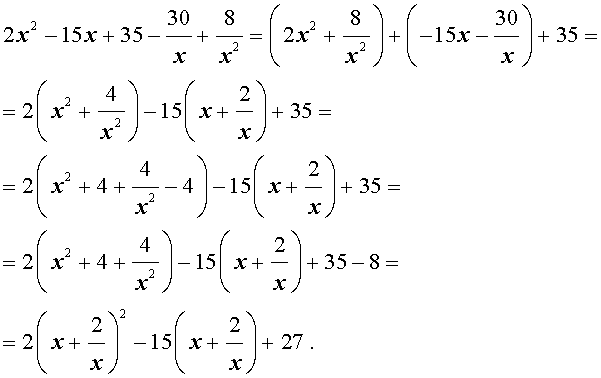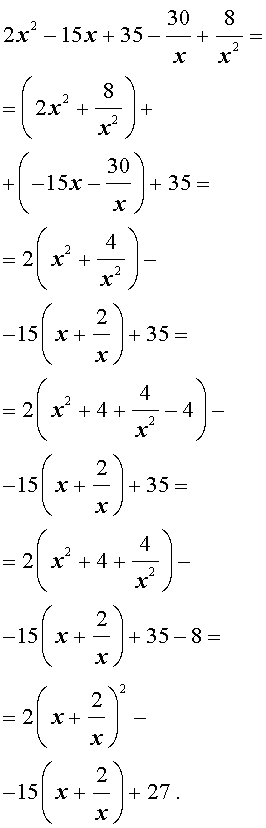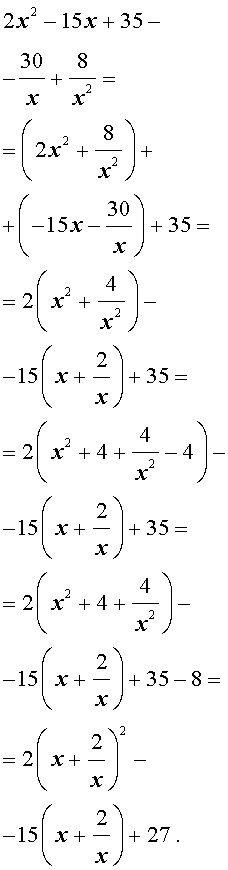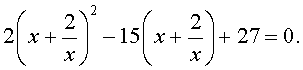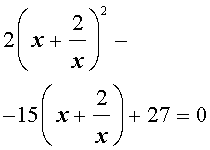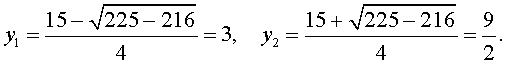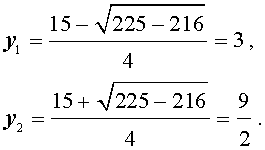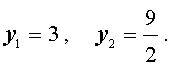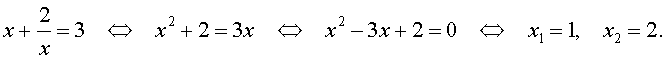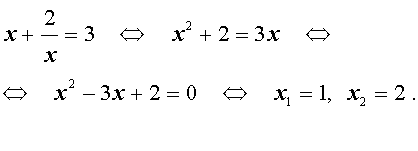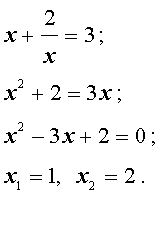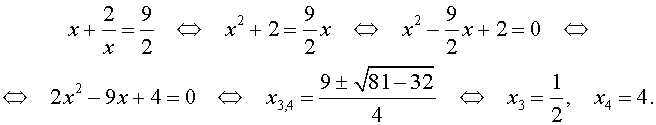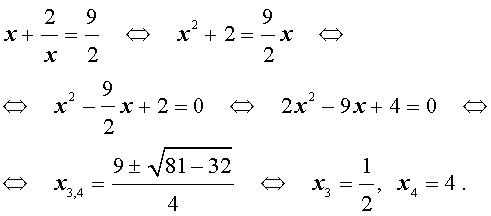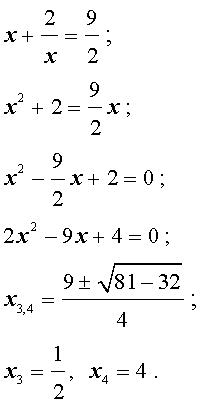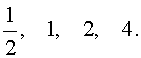Про уравнения - легко » Статьи

Возвратные уравнения 10 кл алгоритм решения

Обновлено
ТЕМА «СИММЕТРИЧЕСКИЕ И ВОЗВРАТНЫЕ УРАВНЕНИЯ»
элективный курс по алгебре (10 класс) по теме

Лекция 1. Симметрические уравнения третьей и четвертой степени.

Лекция 2. Возвратные уравнения.

Лекция 3. Уравнения четвертой степени с дополнительными условиями на коэффициенты.

Семинар 1. Решение симметрических и возвратных уравнений.

Практическая работа 1. Решение симметрических уравнений.

Практическая работа 2. Решение возвратных уравнений.

Самостоятельная работа. Решение симметрических и возвратных уравнений.

Содержание
  1. Скачать:
  2. Предварительный просмотр:
  3. По теме: методические разработки, презентации и конспекты
  4. Уравнения, сводящиеся к квадратным уравнениям: возвратные (симметричные) уравнения
  5. Возвратные (симметричные) уравнения 3-ей степени
  6. Возвратные (симметричные) уравнения 4-ой степени
  7. Обобщенные возвратные уравнения 4-ой степени
  8. Решение возвратных уравнений (урок).
  9. Дистанционное обучение как современный формат преподавания
  10. Математика: теория и методика преподавания в образовательной организации
  11. Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
  12. Дистанционные курсы для педагогов
  13. Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
  14. Материал подходит для УМК
  15. Другие материалы
  16. Вам будут интересны эти курсы:
  17. Оставьте свой комментарий
  18. Автор материала
  19. Дистанционные курсы для педагогов
  20. Подарочные сертификаты
  21. 🎥 Видео

Видео:9 класс. Алгебра. Решение уравнений четвертой степени. Возвратные уравнения.Скачать

9 класс. Алгебра. Решение уравнений четвертой степени. Возвратные уравнения.

Скачать:

ВложениеРазмер
razrabotka_temy_elektivnogo_predmeta.rar8.9 КБ

Видео:Симметрические уравненияСкачать

Симметрические уравнения

Предварительный просмотр:

ТЕМА «СИММЕТРИЧЕСКИЕ И ВОЗВРАТНЫЕ УРАВНЕНИЯ»

Учитель математики МБОУ СОШ № 34 г. Тихорецка Мирошниченко В.Н.

ТЕМА 3 «СИММЕТРИЧЕСКИЕ И ВОЗВРАТНЫЕ УРАВНЕНИЯ»

Лекция 1. Симметрические уравнения третьей и четвертой степени.

Лекция 2. Возвратные уравнения.

Лекция 3. Уравнения четвертой степени с дополнительными условиями на коэффициенты.

Семинар 1 . Решение симметрических и возвратных уравнений.

Практическая работа 1. Решение симметрических уравнений.

Практическая работа 2 . Решение возвратных уравнений.

Самостоятельная работа . Решение симметрических и возвратных уравнений.

Методическая разработка первого занятия по данной теме.

Цель изучения данной темы:

— расширить знания о видах уравнений;

— познакомить с методами их решения;

— учить решать трудные задачи.

Лекция 1. Симметрические уравнения третьей и четвертой степени.

ах 3 + вх 2 + вх + а = 0, а ≠ 0, (1)

называются симметрическими уравнениями третьей степени . Поскольку ах 3 + вх 2 + вх + а = а (х 3 + 1) + вх (х+1) = а (х+ 1) (х 2 — х+ 1) + вх (х+ 1) = (х+1) (ах 2 + (в — а) х + а), то уравнение (1) равносильно совокупности уравнений

х + 1 = 0 и ах 2 + (в — а) х + а = 0, решить которую просто.

Пример 1. Решить уравнение

3х 3 + 4х 2 + 4х + 3 = 0.

Уравнение является симметрическим уравнением третьей степени. Разложим на множители левую часть уравнения

3х 3 + 4х 2 + 4х + 3 = 3 (х 3 + 1) + 4х (х + 1) = ( х + 1) (3х 3 – 3х + 3 + 4х) = ( х+ 1) (3х 3 + х + 3).

Уравнение равносильно совокупности уравнений

х + 1 = 0 и 3х 3 + х + 3 = 0,

ах 4 + вх 3 + сх 2 + вх + а = 0 , а≠ 0,

называются симметрическими уравнениями четвертой степени.

Поскольку х = 0 не является корнем уравнения , то , разделив обе части уравнения на х 2 , получим уравнение . равносильное исходному:

ах 2 + а/х 2 + вх + в/х + с = 0.

Перепишем уравнение в виде:

а [(х + 1/х) 2 — 2 ] + в ( х + 1/х) + с = 0.

В этом уравнении сделаем замену х + 1/х = у. тогда получим квадратное уравнение

ау 2 + ву +с – 2а = 0.

Если уравнение имеет два корня у 1 и у 2 , то исходное уравнение равносильно совокупности уравнений

х 2 — х у 1 + 1 = 0 и х 2 — х у 2 + 1 = 0.

Если же уравнение имеет один корень у 0 , то исходное уравнение равносильно уравнению х 2 — у 0 х = 1 = 0.

Если уравнение не имеет корней, то и исходное уравнение не имеет корней.

Пример 2. Решить уравнение

х 4 – 5х 3 + 8х 2 – 5х- 1 =0.

Решение. Данное уравнение является симметрическим уравнением четвертой степени. Так как х= 0 не является его корнем, то , разделив уравнение на х 2 ,получим равносильное ему уравнение

х 2 – 5х + 8 – 5/х + 1/ х 2 = 0.

Сгруппировав слагаемые, перепишем уравнение в виде

(х 2 + 1/ х 2 ) 2 – 5 (х + 1/х) + 6 =0.

Пусть х + 1/х = у, получим уравнение

имеющее два корня у 1 = 2, у 2 = 3. Следовательно, исходное уравнение равносильно совокупности уравнений

х + 1/х =2 и х + 1/х =3.

Решение первого уравнения этой совокупности есть х 1 = 1, а решения второго есть х 2 =(3+√5)/2, х 3 =(3-√5)/2.

Следовательно, исходное уравнение имеет три корня.

Ответ: х 1 = 1, х 2 =(3+√5)/2, х 3 =(3-√5)/2.

  1. Домашнее задание: рассмотреть решение уравнений;

А) 7х 3 — 5х 2 — 5х + 7 = 0,

Б) 3х 3 + 4х 2 — 4х — 3 = 0,

С) 3х 4 – 4х 3 + 2х 2 – 4х + 3=0,

Д) х 4 +4х 3 — 2х 2 –+4х + 1=0.

Видео:Как решать возвратные уравнения?Скачать

Как решать возвратные уравнения?

По теме: методические разработки, презентации и конспекты

Занятие по теме «Решение простейших тригонометрических уравнений. Уравнение tgx=a»

Занятие проводилось в рамках программы ШТК по математике. Презентация выполнена в программе Смарт и демонстрируется на интерактивной доске.Архив содержит все необходимые материалы.

урок по теме «Примеры решения тригонометрических уравнений и систем уравнений»

Класс 10Урок закрепления.

Возвратные уравнения 10 кл алгоритм решения

Тема 15. ИТОГОВЫЙ КОНТРОЛЬ ПО ТЕМАМ 9-14: «Показательные уравнения. Показательно-степенные уравнения. Показательные неравенства. Преобразования и вычисления логарифмических выражений. Логарифмические уравнения. Логарифмические неравенства».

Уважаемые коллеги!Актуальной задачей на сегодняшний день является качественная подготовка учащихся к единому государственному экзамену (ЕГЭ) по математике, а также абитуриентов к вступител.

Возвратные уравнения 10 кл алгоритм решения

урок по теме «Способы решения тригонометрических уравнений»(урок одного уравнения) 08.03.16

методическая разработка урока алгебры и начал математического анализа в 10 классе по УМК Мордкович, содержит спсобы решения тригонометрического уравнения вида asinx +bcosx=c.

Возвратные уравнения 10 кл алгоритм решения

Дидактический материал по темам: «Логарифмическая функция. Логарифмические уравнения, неравенства и системы», «Показательная функция. Показательные уравнения, системы и неравества»

Тренировочные задания по темам:«Показательная функция. Показательные уравнения, неравенства и системы»«Логарифмическая функция. Логарифмические уравнения, неравенства и системы»Данный дидак.

Возвратные уравнения 10 кл алгоритм решения

Презентации по теме «Системы двух линейных уравнений», «Метод подстановки для решения систем уравнений», «Метод сложения для решения систем уравнений» .

Презентации проедполагает использование при проведении онлайн урока по теме «Системы двух линейных уравнений», «Метод подстановки для решения систем уравнений», «Метод сложени.

Возвратные уравнения 10 кл алгоритм решения

Научная статья на тему: «Симметрические многочлены»

Научная статья на тему: «Симметрические многочлены&quot.

Видео:СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

СУПЕР ЛАЙФХАК — Как решать Иррациональные Уравнения

Уравнения, сводящиеся к квадратным уравнениям:
возвратные (симметричные) уравнения

Существует ряд уравнений, которые удается решить при помощи сведения их к квадратным уравнениям.

К таким уравнениям, в частности, относятся уравнения следующих типов:

Возвратные уравнения 10 кл алгоритм решенияТрёхчленные уравнения
Возвратные уравнения 10 кл алгоритм решенияУравнения 4-ой степени, левая часть которых равна произведению четырёх последовательных членов арифметической прогрессии
Возвратные уравнения 10 кл алгоритм решенияВозвратные (симметричные) уравнения 3-ей степени
Возвратные уравнения 10 кл алгоритм решенияВозвратные (симметричные) уравнения 4-ой степени
Возвратные уравнения 10 кл алгоритм решенияОбобщенные возвратные уравнения 4-ой степени

Замечание . Уравнения, носящие название «Биквадратные уравнения» , относятся к типу «Трехчленные уравнения» .

Видео:Решение тригонометрических уравнений. Однородные уравнения. 10 класс.Скачать

Решение тригонометрических уравнений. Однородные уравнения. 10 класс.

Возвратные (симметричные) уравнения 3-ей степени

Возвратным уравнением 3-ей степени называют уравнение вида

a x 3 + b x 2 + b x + a = 0,(1)

где a , b – заданные числа.

Решение уравнения (1) осуществляется при помощи разложения левой части уравнения (1) на множители:

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Для завершения решения уравнения (1) остаётся лишь решить квадратное уравнение

Пример 1 . Решить уравнение

2x 3 + 7x 2 + 7x + 2 = 0.(2)

Решение . Разложим левую часть уравнения (2) на множители:

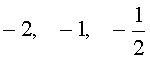
Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Ответ :Возвратные уравнения 10 кл алгоритм решения.

Видео:14 Урок Симметрические и возвратные уравненияСкачать

14 Урок Симметрические и возвратные уравнения

Возвратные (симметричные) уравнения 4-ой степени

Возвратными (симметричными) уравнениями 4-ой степени называют уравнения вида

a x 4 + b x 3 + cx 2 +
+ b x + a = 0,		(3)

а также уравнения вида

a x 4 + b x 3 + cx 2 –
– b x + a = 0,		(4)

Для того, чтобы решить возвратное уравнение (3), разделим его на x 2 . В результате получится уравнение

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Преобразуем левую часть уравнения (5):

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

В результате этого преобразования уравнение (5) принимает вид

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Если теперь обозначить

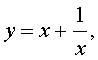Возвратные уравнения 10 кл алгоритм решения(7)

то уравнение (6) станет квадратным уравнением:

a y 2 + b y + c – 2 a = 0.(8)

Найдем корни уравнения (8), а после этого, подставив каждый из найденных корней в равенство (7), решим полученное уравнение относительно x .

Описание метода решения уравнений вида (3) завершено.

Для того, чтобы решить возвратное уравнение (4), разделим его на x 2 . В результате получится уравнение

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Преобразуем левую часть уравнения (9):

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

В результате этого преобразования уравнение (9) принимает вид

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Если теперь обозначить

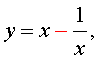Возвратные уравнения 10 кл алгоритм решения(11)

то уравнение (10) станет квадратным уравнением:

a y 2 + b y + c + 2 a = 0.(12)

Найдем корни уравнения (13), а после этого, подставив каждый из найденных корней в равенство (11), решим полученное уравнение относительно x .

Описание метода решения уравнений вида (4) завершено.

Пример 2 . Решить уравнение

2x 4 – 3x 3 – x 2 –
– 3x + 2 = 0.		(13)

Решение . Уравнение (13) является возвратным и относится к виду (3). Разделим его на x 2 . В результате получится уравнение

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Преобразуем левую часть уравнения (14):

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

В результате этого преобразования уравнение (14) принимает вид

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Если теперь обозначить

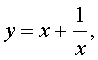Возвратные уравнения 10 кл алгоритм решения(16)

то уравнение (15) станет квадратным уравнением:

2y 2 – 3y – 5 = 0.(17)
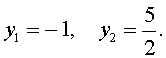Возвратные уравнения 10 кл алгоритм решения(18)

В первом случае из равенства (16) получаем уравнение:

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

которое решений не имеет.

Во втором случае из равенства (16) получаем:

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Ответ : Возвратные уравнения 10 кл алгоритм решения

Пример 3 . Решить уравнение

6x 4 – 25x 3 + 12x 2 +
+ 25x + 6 = 0.		(19)

Решение . Уравнение (19) является возвратным и относится к виду (4). Разделим его на x 2 . В результате получится уравнение

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Преобразуем левую часть уравнения (20):

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

В результате этого преобразования уравнение (20) принимает вид

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Если теперь обозначить

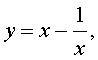Возвратные уравнения 10 кл алгоритм решения(22)

то уравнение (21) станет квадратным уравнением:

6y 2 – 25y + 24 = 0.(23)
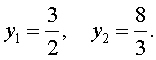Возвратные уравнения 10 кл алгоритм решения(24)

В первом случае из равенства (22) получаем:

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Во втором случае из равенства (22) получаем:

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Ответ : Возвратные уравнения 10 кл алгоритм решения

Видео:10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

10 класс, 23 урок, Методы решения тригонометрических уравнений

Обобщенные возвратные уравнения 4-ой степени

Обобщенным возвратным уравнением 4-ой степени назовём уравнение вида

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

где a , b , c, d – заданные числа.

Для того, чтобы решить уравнение (25), разделим его на x 2 . В результате получится уравнение

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Преобразуем левую часть уравнения (26):

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

В результате этого преобразования уравнение (26) принимает вид

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Если теперь обозначить

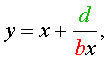Возвратные уравнения 10 кл алгоритм решения(28)

то уравнение (27) станет квадратным уравнением:

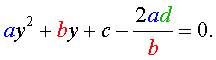Возвратные уравнения 10 кл алгоритм решения(29)

Найдем корни уравнения (29), а после этого, подставив каждый из найденных корней в равенство (28), решим полученное уравнение относительно x .

Описание метода решения уравнений вида (25) завершено.

Пример 4 . Решить уравнение

2x 4 – 15x 3 + 35x 2 –
– 30 x + 8 = 0.		(30)

Решение . Введем для коэффициентов уравнения (30) следующие обозначения

и найдем значение выражения

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

то уравнение (30) является обобщенным возвратным уравнением 4-ой степени. В соответствии с изложенным выше, разделим его на x 2 . В результате получится уравнение

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Преобразуем левую часть уравнения (31):

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

В результате этого преобразования уравнение (31) принимает вид

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Если теперь обозначить

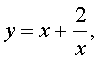Возвратные уравнения 10 кл алгоритм решения(33)

то уравнение (32) станет квадратным уравнением:

2y 2 – 15y + 27 = 0.(34)

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

В первом случае из равенства (33) получаем:

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Во втором случае из равенства (33) получаем:

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Ответ : Возвратные уравнения 10 кл алгоритм решения

Видео:Рациональные уравнения №2. Возвратные уравнения 4-й степени. ЕГЭ математика профиль 2023. Задание 12Скачать

Рациональные уравнения №2. Возвратные уравнения 4-й степени. ЕГЭ математика профиль 2023. Задание 12

Решение возвратных уравнений (урок).

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Решение возвратных целых уравнений с помощью введения новой переменной.

Урок изучения нового материала.

Цели: рассмотреть один из видов целых уравнений – возвратные уравнения 4 степени, научиться их решать; совершенствовать навык решения целых уравнений, в том числе, методом введения новой переменной, подготовка к экзамену.

Актуализация знаний: решение заданий из открытого банка заданий ОГЭ.

1. Возвратные уравнения 10 кл алгоритм решенияОтвет: -2.

2. Возвратные уравнения 10 кл алгоритм решенияОтвет: -3; 6.

3. Возвратные уравнения 10 кл алгоритм решенияОтвет: 4

4. Возвратные уравнения 10 кл алгоритм решенияОтвет: х

5. Возвратные уравнения 10 кл алгоритм решенияОтвет: -1 x

6. Возвратные уравнения 10 кл алгоритм решенияОтвет:

Изучение нового материала: Возвратные уравнения 4 степени, это уравнения вида:

Возвратные уравнения 10 кл алгоритм решения

1.Разделить обе части уравнения на х 2 .

2.Сгруппировать слагаемые (первый с последним, второй с четвёртым).

Привести уравнение к виду а Возвратные уравнения 10 кл алгоритм решения+ с = 0

3. Ввести новую переменную t = Возвратные уравнения 10 кл алгоритм решения, тогда выполнено t 2 = Возвратные уравнения 10 кл алгоритм решения, т.е. Возвратные уравнения 10 кл алгоритм решения= t 2 – 2.

4. Выполнить подстановку и решить квадратное уравнение.

5.Вернуться к замене и решить получившиеся уравнения.

Возвратные уравнения 10 кл алгоритм решения

Возвратные уравнения 10 кл алгоритм решения

Закрепление материала: Решение заданий: 7. Ответ: 0,5; 2.

8. Ответ: -0,5; -1/3; 2; 3.

Подведение итогов. Выставление отметок. Домашнее задание: п. 16, № 350, 373 а), 370 а).

Возвратные уравнения 10 кл алгоритм решения

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

  • Сейчас обучается 925 человек из 80 регионов

Возвратные уравнения 10 кл алгоритм решения

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

  • Сейчас обучается 684 человека из 75 регионов

Возвратные уравнения 10 кл алгоритм решения

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

  • Сейчас обучается 309 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Возвратные уравнения 3 степениСкачать

Возвратные уравнения 3 степени

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 577 795 материалов в базе

Материал подходит для УМК

Возвратные уравнения 10 кл алгоритм решения

«Алгебра», Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. / Под ред. Теляковского С.А.

§ 3. Квадратичная функция и ее график

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Другие материалы

  • 10.12.2017
  • 954
  • 13

Возвратные уравнения 10 кл алгоритм решения

  • 10.12.2017
  • 1135
  • 13

Возвратные уравнения 10 кл алгоритм решения

  • 10.12.2017
  • 1658
  • 25

Возвратные уравнения 10 кл алгоритм решения

  • 10.12.2017
  • 457
  • 3

Возвратные уравнения 10 кл алгоритм решения

  • 10.12.2017
  • 692
  • 0

Возвратные уравнения 10 кл алгоритм решения

  • 10.12.2017
  • 232
  • 0
  • 10.12.2017
  • 323
  • 0
  • 10.12.2017
  • 412
  • 0

Возвратные уравнения 10 кл алгоритм решения

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

  • 10.12.2017 1976
  • DOCX 196.5 кбайт
  • 22 скачивания
  • Оцените материал:

Настоящий материал опубликован пользователем Максименко Светлана Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

Возвратные уравнения 10 кл алгоритм решения

  • На сайте: 5 лет и 6 месяцев
  • Подписчики: 0
  • Всего просмотров: 38970
  • Всего материалов: 26

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 10 класс решение показательных уравненийСкачать

ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 10 класс решение показательных уравнений

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Возвратные уравнения 10 кл алгоритм решения

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Возвратные уравнения 10 кл алгоритм решения

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Возвратные уравнения 10 кл алгоритм решения

В Воронеже продлили удаленное обучение для учеников 5-11-х классов

Время чтения: 1 минута

Возвратные уравнения 10 кл алгоритм решения

Объявлен конкурс дизайн-проектов для школьных пространств

Время чтения: 2 минуты

Возвратные уравнения 10 кл алгоритм решения

Профессия педагога на третьем месте по популярности среди абитуриентов

Время чтения: 1 минута

Возвратные уравнения 10 кл алгоритм решения

Приемная кампания в вузах начнется 20 июня

Время чтения: 1 минута

Возвратные уравнения 10 кл алгоритм решения

Тринадцатилетняя школьница из Индии разработала приложение против буллинга

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

🎥 Видео

Как решить симметрическое уравнение | Сведение к квадратному | Замена переменнойСкачать

Как решить симметрическое уравнение | Сведение к квадратному | Замена переменной

Как решать неравенства? Математика 10 класс | TutorOnlineСкачать

Как решать неравенства? Математика 10 класс | TutorOnline

Уравнение четвертой степениСкачать

Уравнение четвертой степени

ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

ПРОСТЕЙШИЙ способ решения Показательных Уравнений

Решение биквадратных уравнений. 8 класс.Скачать

Решение биквадратных уравнений. 8 класс.

Простейшие тригонометрические уравнения. y=sinx. 1 часть. 10 класс.Скачать

Простейшие тригонометрические уравнения. y=sinx. 1 часть. 10 класс.

Схема Горнера. 10 класс.Скачать

Схема Горнера. 10 класс.

Решение тригонометрических уравнений. 10 класс.Скачать

Решение тригонометрических уравнений. 10 класс.

Алгебра 10 класс (Урок№20 - Иррациональные уравнения и неравенства.)Скачать

Алгебра 10 класс (Урок№20 - Иррациональные уравнения и неравенства.)

Как решают уравнения в России и США!?Скачать

Как решают уравнения в России и США!?
Поделиться или сохранить к себе: