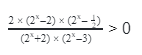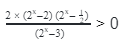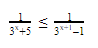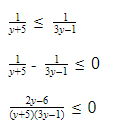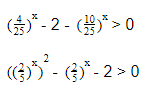- Метод возведения в степень
- Пример №220.
- Пример №221.
- Пример №222.
- Пример №223.
- Пример №224.
- Пример №225.
- Показательные уравнения и неравенства с примерами решения
- Решении показательных уравнений
- Показательные уравнения и их системы
- Пример №1
- Пример №2
- Пример №3
- Пример №4
- Пример №5
- Пример №6
- Системы простейших показательных уравнений
- Пример №7
- Пример №8
- Пример №9
- Приближенное решение уравнений
- Пример №10
- Нахождение приближенного корня с заданной точностью
- Пример №11
- Показательные неравенства
- Определение показательных неравенств
- Как решать показательные неравенства
- Показательные неравенства, сводящиеся к простейшим
- Пример 1
- Показательные неравенства, сводящиеся к квадратным
- Пример 1
- Показательные неравенства, сводящиеся к рациональным
- Пример 1
- Пример 2
- Однородные показательные неравенства
- Пример 1
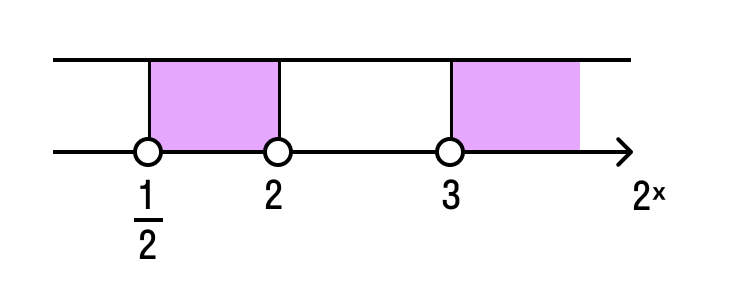
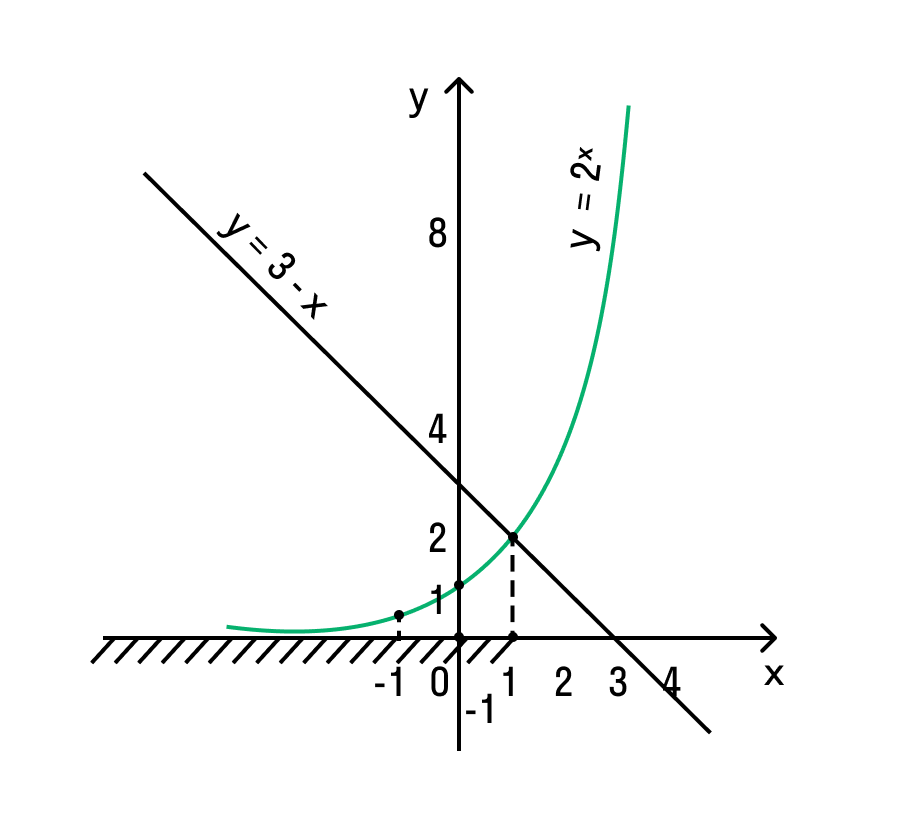
- Неравенства, решаемые графическим методом
- Пример 1
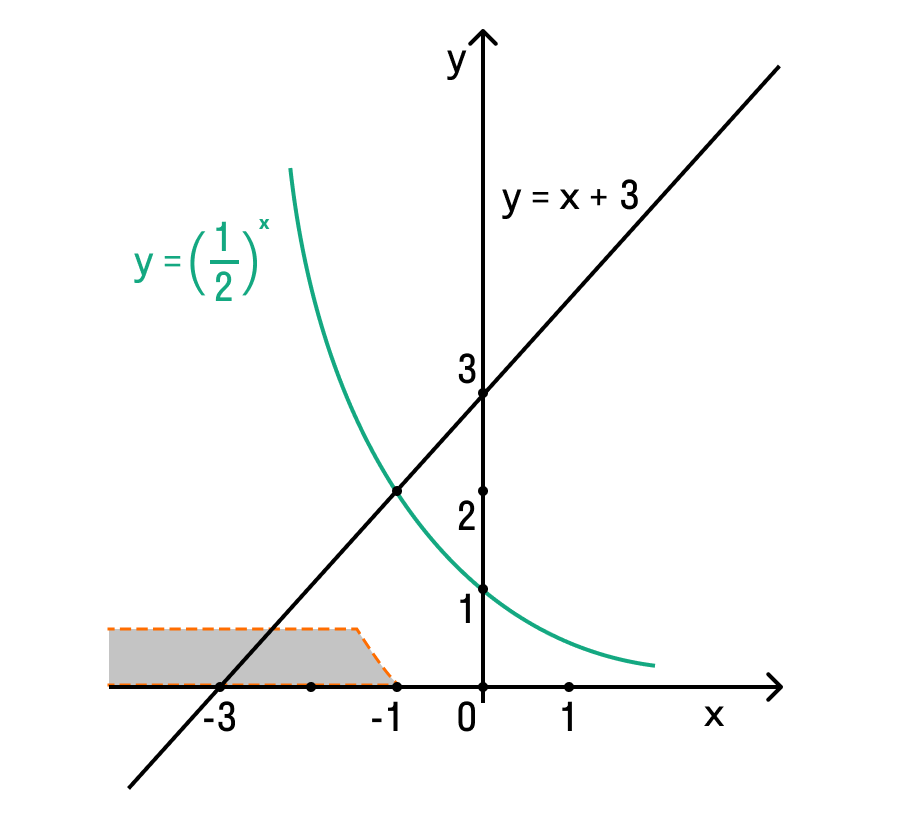
- Пример 2
- 🔍 Видео
Метод возведения в степень
Метод возведения в степень является одним из наиболее распространённых методов решения задач с иррациональностями. Как уже отмечалось выше, при его использовании следует помнить, что любое уравнение и неравенство всегда можно возвести в нечётную степень, это преобразование является равносильным. Другое дело, если уравнение необходимо возвести в чётную степень. В общем случае это переход к следствию, чреватый появлением посторонних корней. Это допустимо, если возможно сделать проверку корней. Если же проверка по какой-либо причине затруднена или невозможна (например, когда при решении неравенств и некоторых уравнений получается бесконечно много решений), то следует сохранять равносильность выполняемых преобразований. Для этого перед очередным возведением в чётную степень следует не забывать выписывать условие неотрицательности обеих частей уравнения.
Если уравнение содержит несколько радикалов, то для последовательного избавления от них уравнение приходится возводить в степень несколько раз. В этом случае перед очередным возведением в степень часто используют приём уединения корня.
Пример №220.
Решение:
ОДЗ :
Далее метод возведения в степень (в данном случае в квадрат, так как в уравнение входят квадратные корни) можно применить двумя способами.
1-й способ. Приведём уравнение к виду
Обе части уравнения неотрицательны, поэтому, возведя его в квадрат, получим равносильное (на ОДЗ) уравнение:
2-й способ. Сразу возведём уравнение в квадрат
(переход к следствию) и, упростив, запишем в виде
Разложим полученное уравнение на множители
и сведём к совокупности
Так как в процессе решения задачи был переход к следствию, то необходимо сделать проверку полученных значений x подстановкой в ОДЗ или исходное уравнение (или в любое уравнение, равносильное исходному). Число 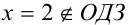
Пример №221.
Решение:
1-й способ. Возведём неравенство в куб, используя формулу
Заменяя, в силу исходного уравнения, выражение 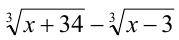
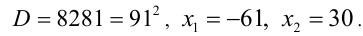
2-й способ. Приведём уравнение к виду
и после этого возведём его в куб:
Решая это уравнение как квадратное относительно 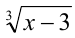
откуда получаем те же значения x .
Следует отметить, что второй способ в данном случае предпочтительней, так как полученное в конце квадратное уравнение имеет более простые коэффициенты (и не надо делать проверку). Ответ:
Пример №222.
Решение:
Возведём обе части уравнения в куб (равносильное преобразование):
Заменяя выражение 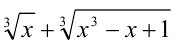
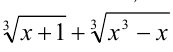
Это уравнение сводится к совокупности двух уравнений:
Решения первого уравнения есть 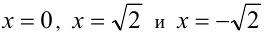
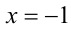
Пример №223.
Решение:
Выпишем ОДЗ: 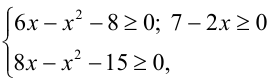
добившись того, чтобы обе части неравенства стали неотрицательны (иначе неравенство возводить в квадрат нельзя). Только после этого возведём в квадрат, перейдя к равносильному (на ОДЗ) неравенству
После упрощения получим
Пример №224.
Решение:
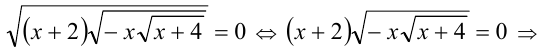
Проверка подстановкой в исходное уравнение показывает, что все три числа являются решениями уравнения.
Замечание. Иногда при решении этой задачи записывают ОДЗ так:
Хочется предостеречь читателя от таких попыток, поскольку первые два условия в системе неверны, что подтверждается наличием среди корней уравнения числа 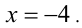
Пример №225.
Решение:
Заметим, что x = -2 и x = 0 являются решениями уравнения (а числа x = — 4 и x = -3 — не являются). Найдём корни этого уравнения, отличные от x = -2 и x = 0 . Для них, согласно ОДЗ,
Возведём уравнение в квадрат, получив равносильное (на ОДЗ) уравнение:
Обе части последнего равенства положительны при — 2
Сократив на x+ 2(> 0) и х(
обе части которого отрицательны при -2
корни которого
Ответ:
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:НЕРАВЕНСТВА возведение в степень 9 класс МакарычевСкачать

Показательные уравнения и неравенства с примерами решения
Содержание:
Рассмотрим уравнения, в которых переменная (неизвестное) находится в показателе степени. Например:
Уравнения такого вида принято называть показательными.
Видео:Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать

Решении показательных уравнений
При решении показательных уравнений нам будет полезно следствие из теоремы о свойствах показательной функции.
Пусть
Каждому значению показательной функции 
Пример:
Решение:
Согласно следствию из равенства двух степеней с одинаковым основанием 3 следует равенство их показателей. Таким образом, данное уравнение равносильно уравнению
Пример:
Решение:
а) Данное уравнение равносильно (поясните почему) уравнению
Если степени с основанием 3 равны, то равны и их показатели:
Решив это уравнение, получим
Ответ:
При решении каждого уравнения из примера 2 сначала обе части уравнения представили в виде степени с одним и тем же основанием, а затем записали равенство показателей этих степеней.
Пример:
Решение:
а) Данное уравнение равносильно уравнению
Решая его, получаем:
Так как две степени с одинаковым основанием 2 равны, то равны и их показатели, т. е. 
б) Разделив обе части уравнения на 

Ответ:
При решении примера 3 а) левую часть уравнения разложили на множители. Причем за скобку вынесли такой множитель, что в скобках осталось числовое выражение, не содержащее переменной.
Пример:
Решить уравнение
Решение:
Обозначим 
Таким образом, из данного уравнения получаем
откуда находим:
Итак, с учетом обозначения имеем:
При решении примера 4 был использован метод введения новой переменной, который позволил свести данное уравнение к квадратному относительно этой переменной.
Пример:
Решить уравнение
Решение:
Можно заметить, что 2 — корень данного уравнения. Других корней уравнение не имеет, так как функция, стоящая в левой части уравнения, возрастающая, а функция, стоящая в правой части уравнения, убывающая. Поэтому уравнение имеет не более одного корня (см. теорему из п. 1.14).
Пример:
Решить уравнение
Решение:
Пример:
При каком значении а корнем уравнения 
Решение:
Поскольку х = 2 — корень, то верно равенство
Решив это уравнение, найдем
Ответ: при
Показательные уравнения и их системы
Показательным уравнением называется уравнение, в ко тором неизвестное входит в показатель степени. При решении показательных уравнений полезно использовать следующие тождества:
Приведем методы решения некоторых типов показательных уравнений.
1 Приведение к одному основанию.
Метод основан на следующем свойстве степеней: если две степени равны и равны их основания, то равны и их показатели, т.е. уравнения надо попытаться привести к виду 
Пример №1
Решите уравнение
Решение:
Заметим, что 
Применив тождество (1), получим Зх — 7 = -7х + 3, х = 1.
Пример №2
Решить уравнение
Решение:
Переходя к основанию степени 2, получим:
Согласно тождеству (2), имеем
Последнее уравнение равносильно уравнению 4х-19 = 2,5х.
2 Введение новой переменной.
Пример №3
Решить уравнение
Решение:
Применив тождество 2, перепишем уравнение как
Введем новую переменную: 
которое имеет корни 


Пример №4
Решить уравнение
Решение:
Разделив обе части уравнения на 
последнее уравнение запишется так:
Решая уравнение, найдем
Значение 

Пример №5
Решить уравнение
Решение:
Заметим что 
Перепишем уравнение в виде
Обозначим 
Получим
Корнями данного уравнения будут
Следовательно,
III Вынесение общего множителя за скобку.
Пример №6
Решить уравнение
Решение:
После вынесения за скобку в левой части 



Системы простейших показательных уравнений
Пример №7
Решите систему уравнений:
Решение:
По свойству степеней система уравнений равносильна следующей
системе :
Очевидно, что последняя система имеет решение
Пример №8
Решите систему уравнений:
Решение:
По свойству степеней система уравнений равносильна следующей системе: 
Умножив второе уравнение этой системы на (-2) и сложив с первым, получим уравнение —9х=-4. Отсюда, найдем 
Пример №9
Решите систему уравнений:
Решение:
Сделаем замену: 
Очевидно, что эта система уравнений имеет решение
Тогда получим уравнения
Приближенное решение уравнений
Пусть многочлен f(х) на концах отрезка [a,b] принимает значения разных знаков, то есть 

Это утверждение проиллюстрировано на следующем чертеже.
Рассмотрим отрезок 
Метод последовательного деления отрезка пополам заключается в последовательном разделении отрезка [a, b] пополам до тех пор, пока длина полученного отрезка не будет меньше заданной точности
- вычисляется значение f(х) выражения
- отрезок делится пополам, то есть вычисляется значение
- вычисляется значение
выражения f(х) в точке
- проверяется условие
- если это условие выполняется, то в качестве левого конца нового отрезка выбирается середина предыдущего отрезка, то есть полагается, что
(левый конец отрезка переходит в середину);
- если это условие не выполняется, то правый конец нового отрезка переходит в середину, то есть полагается, что b=x;
- для нового отрезка проверяется условие
- если это условие выполняется , то вычисления заканчиваются. При этом в качестве приближенного решения выбирается последнее вычисленное значение х. Если это условие не выполняется, то, переходя к пункту 2 этого алгоритма, вычисления продолжаются.
Метод последовательного деления пополам проиллюстрирован на этом чертеже:
Для нахождения интервала, содержащего корень уравнения 
Оказывается, что для корня 


Пример №10
Найдите интервал, содержащий корень уравнения
Решение:
Поделив обе части уравнения на 2 , получим,
Так как, для нового уравнения
Значит, в интервале, 




Значит, уравнение имеет корень, принадлежащий интервалу (-1; 0).
Нахождение приближенного корня с заданной точностью
Исходя из вышесказанного, заключаем, что если выполнено неравенство 



корень уравнения с точностью 




Пример №11
Найдите приближенное значение корня уравнения 
Решение:
Из предыдущего примера нам известно, что корень лежит в интервале
(-1; 0). Из того, что 
Так как, |(-0,25)41,5(-0,25)2+2,5(-0,25)+0,5| = |-0,046| 1. Если
Пусть
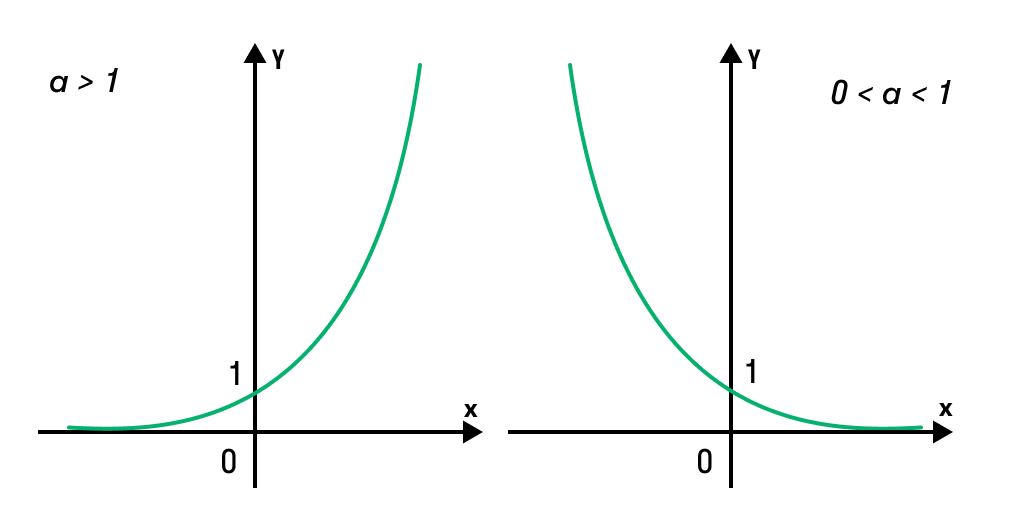
Изображения графиков показательной функции подсказывают это свойство. На рисунке 27 видно, что при а > 1 большему значению функции соответствует большее значение аргумента. А на рисунке 30 видно, что при 0
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Как решать неравенства? Часть 1| МатематикаСкачать

Показательные неравенства
О чем эта статья:
10 класс, 11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Система уравнений VS Система неравенств. ОГЭ по математике №9, 13| Математика TutorOnlineСкачать

Определение показательных неравенств
Показательными считаются неравенства, которые включают в себя показательную функцию. Другими словами, это неравенства с переменной в показателе степени: a f(x) > a g(x) , a f(x) g(x) .
Из них показательно-степенными неравенствами являются те, в которых есть переменные и в показателе степени, и в основании.
Для изучения этой темы стоит повторить:
И, конечно, для решения тригонометрических и логарифмических показательных неравенств также придется вспомнить формулы соответствующих разделов алгебры.
Если все это еще свежо в памяти, давайте приступим. Как и к показательным уравнениям, к неравенствам стоит подходить, помня о свойствах показательной функции. Напомним, что она выглядит так: y = a x , где a > 0 и a ≠ 1. Два графика ниже дают представление о том, на что похожа такая функция, когда основание степени а больше и меньше единицы. Наверняка вы уже догадались, каково главное свойство этой функции. Да, она монотонна.
При этом заметьте — значения а всегда больше нуля. На практике в этом несложно убедиться, если возводить какое-либо число во всевозможные степени, включая отрицательные. Например: 2 -2 = 4, 2 -4 = 1/16 и т. д. Значение функции будет уменьшаться, но никогда не достигнет нуля.
Для любых а и х верно неравенство a x > 0, т. е. показательная функция не принимает отрицательных значений.
Запишем следствие монотонности показательной функции в виде формул:
- a f(x) > a g(x) f(x) > g (x), когда функция возрастает, т. е. а > 1;
- a f(x) > a g(x) f(x)
Видео:СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Как решать показательные неравенства
Как мы уже говорили, для успешного освоения этой темы нужно хорошенько повторить все, что касается показательных уравнений. Способы решения показательных неравенств выглядят примерно так же — мы будем пытаться упростить выражение, получить одинаковые степени или одинаковые основания, по возможности свести все к квадратному или рациональному уравнению. Но есть и свои тонкости.
Допустим, у нас есть простейшее показательное неравенство:
Если вы помните, как решались показательные уравнения, не придется долго думать, что делать с таким неравенством — приведем его к одинаковому основанию:
Казалось бы, все логично, но всегда ли можно смело вычеркивать одинаковые основания степеней? А что, если вместо 3 у нас основание степени будет 0,5? Посмотрим:
Проверим, верно ли в таком случае х > 2.
0,5 3 = 0, 125 и т. д.
Как видите, на самом деле в этом случае х

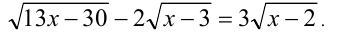
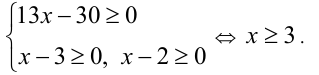
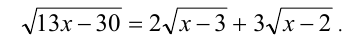
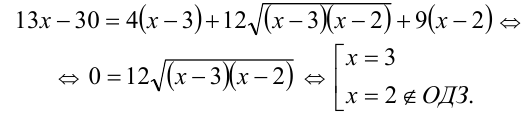
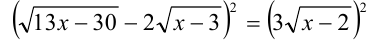
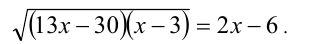
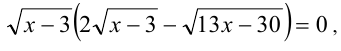
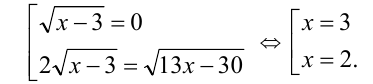
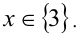
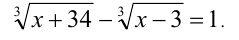
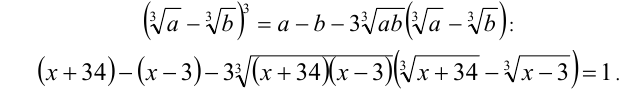
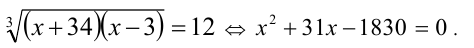
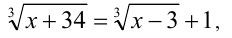
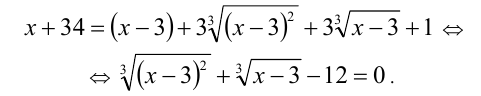
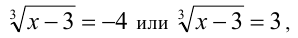
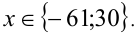
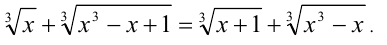
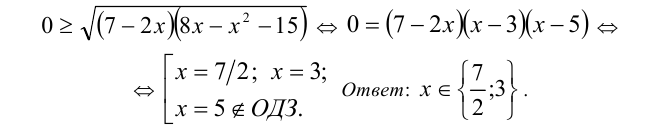
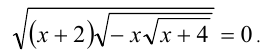
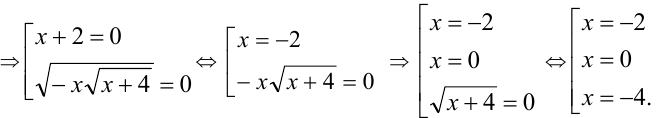
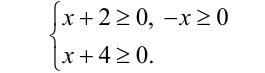
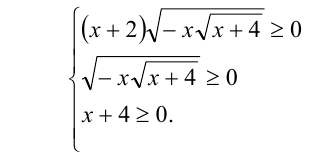
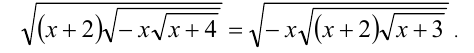
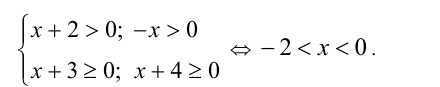
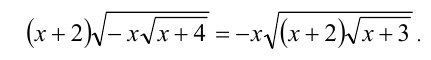
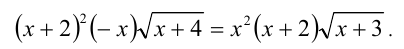
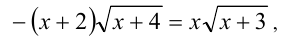
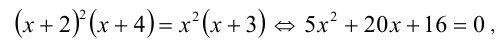
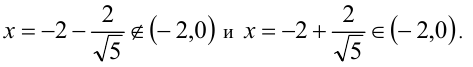
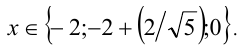











































































 выражения f(х) в точке
выражения f(х) в точке 

 (левый конец отрезка переходит в середину);
(левый конец отрезка переходит в середину);