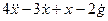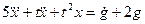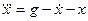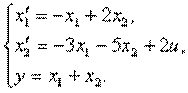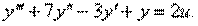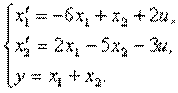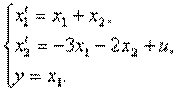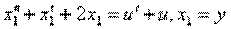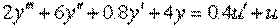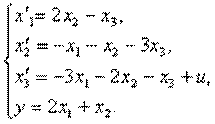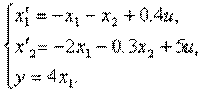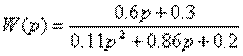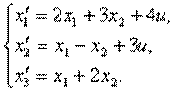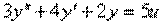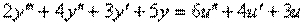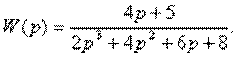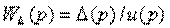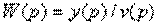- АЛГОРИТМ ПОСТРОЕНИЯ СТРУКТУРНОЙ СХЕМЫ
- Задачи и пример решения одной из них по теме «Структурный метод»
- Страницы работы
- Содержание работы
- Получение структурной схемы по уравнениям
- Построение структурной схемы по системе алгебраических уравнений
- Построение структурной схемы по системе дифференциальных уравнений
- 🔥 Видео
Видео:Восстановление функции по полному дифференциалу. Дифференциальное уравнение в полных дифференциалах.Скачать
АЛГОРИТМ ПОСТРОЕНИЯ СТРУКТУРНОЙ СХЕМЫ
1. Вырачитт. член со старшей производной из дифференциального уравнения (1.3) и представить полученное соотношение с помощью сумматора, дифференцирующих и усилительных звеньев.
2. Все низшие производные получить как сигналы на соответствующих выходах последовательно соединенных интегрирующих звеньев.
3 Начальные условия (1.4) представить как постоянные во времени воздействия, приложенные на выходах интегрирующих звеньев.
Пример 1.1. Построить структурную схему системы, описываемой дифференциальным уравнением
с начальными условиями 
, 
.
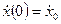
□ Выразим из уравнения член со старшей производной:
.
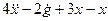
Изобразим схему получения сигнала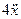 
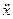
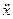
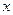
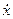
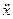
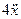
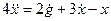
(рис. 1.9). С помощью усилительного члена с коэффициентом усиления 1/4 получим сигнал 
. Построим теперь прямую цепь схемы, последовательно преобразовывая сигнал интегрирующими звеньями. Добавляя на выходах интегрирующих звеньев соответствующие начальные условия, получаем часть прямой цепи схемы, в которой присутствуют выходной сигнал 
и его производные 
, . Изображаем сумматор, выходным сигналом коюрого служит . На этом сумматоре нужно реализовать равенство
.
Для этого добавляем к прямой цепи соединение дифференцирующего и усилительного звеньев, которые из входного сигнала g позволяют получить нужный сигнал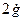 
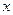
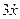
на входе сумматора. Сигналы и 
подаем на сумматор с соответствующим знаком, используя обратные связи. Таким образом, получаем структурную схему (рис. 1.9), соответствующую заданному дифференциальному уравнению.
Пример 1.2. Построить структурную схему системы, описываемой дифференциальным уравнением
с начальными условиями , 
, 
.
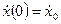
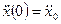
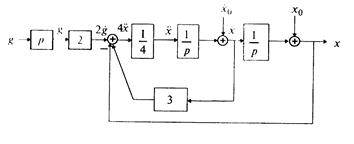
□ Выразим из уравнения член со старшей производной:
.
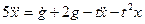
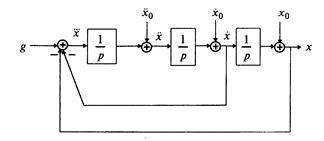
Согласно алгоритму получим структурную схему системы (рис. 1.10).
Пример 1.3. Построить структурную схему системы, описываемой дифференциальным уравнением
.
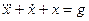
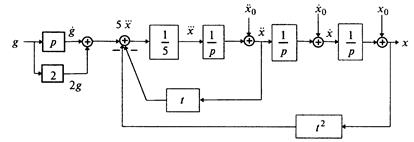
□ Выразим из уравнения член со старшей производной:
и с помощью алгоритма получим схему (рис. 1.11).
2. Составление дифференциального уравнения по структурной схеме. Для записи дифференциального уравнения следует обозначить на схеме все промежуточные сигналы, записать уравнения для каждого звена и для каждого сумматора и из полученной системы дифференциальных и алгебраических уравнений исключить промежуточные переменные кроме входного и выходного сигналов.
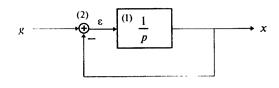
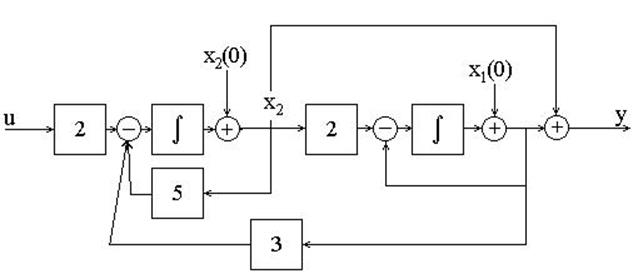
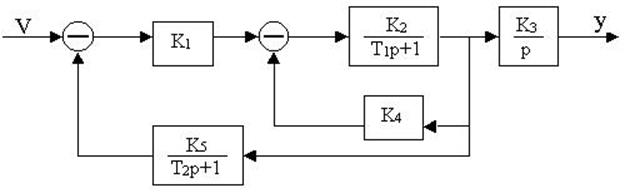
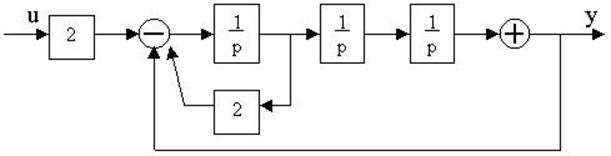
Пример 1.4. Составить дифференциальное уравнение по структурной схеме, изображенной на рис. 1 12.
□ Составим уравнения элементов схемы:
; 
.
, 
, 
.
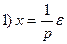
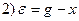
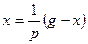
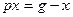
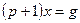
Дифференциальное уравнение системы имеет вид
,
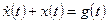
что совпадает с (1.10) при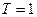 
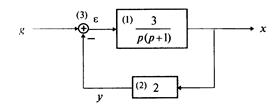
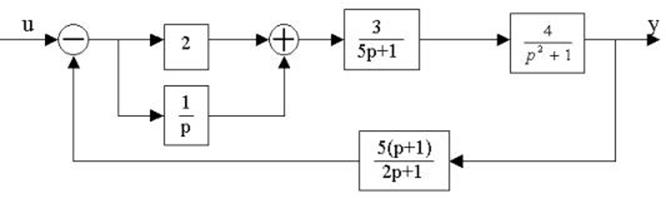
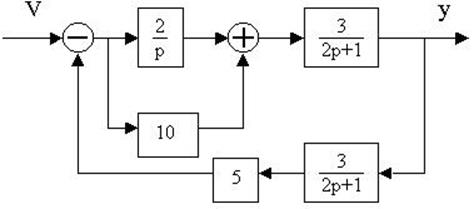
, т.е. система, состоящая из интегрирующего звена, замкнутого отрицательной обратной связью, является апериодическим звеном.
Пример 1.5. Составить дифференциальное уравнение по структурной схеме, представленной на рис. 1.13.
□ Составим уравнения элементов схемы:
; 
; 
.
.
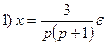
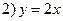
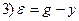
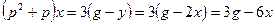
Переходя от операторной формы записи дифференциального уравнения к обычной, получаем
.
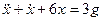
Видео:11. Уравнения в полных дифференциалахСкачать
Задачи и пример решения одной из них по теме «Структурный метод»
Страницы работы
Содержание работы
ТЕМА 4. СТРУКТУРНЫЙ МЕТОД
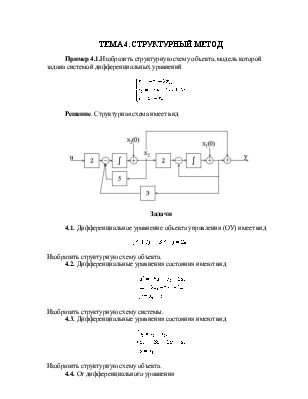
Пример 4.1.Изобразить структурную схему объекта, модель которой задана системой дифференциальных уравнений
Решение. Структурная схема имеет вид
4.1. Дифференциальное уравнение объекта управления (ОУ) имеет вид
Изобразить структурную схему объекта.
4.2. Дифференциальные уравнения состояния имеют вид
Изобразить структурную схему системы.
4.3. Дифференциальные уравнения состояния имеют вид
Изобразить структурную схему объекта.
4.4. От дифференциального уравнения
перейти к структурной схеме.
4.5. От дифференциального уравнения
описывающего объект, перейти к структурной схеме.
4.6. Изобразить структурную схему объекта, модель которого задана системой дифференциальных уравнений
4.7. Известна модель объекта в пространстве состояний
Изобразить структурную схему на интегрирующих элементах.
4.8. По известной передаточной функции объекта
записать дифференциальное уравнение и изобразить структурную схему.
4.9. Представить в виде структурной схемы модель ОУ, заданную системой дифференциальных уравнений
4.10. Представить в виде структурной схемы модель ОУ, заданную дифференциальным уравнением
4.11. Представить в виде структурной схемы модель ОУ, заданную дифференциальным уравнением
4.12. Перейти от передаточной функции к структурной схеме, содержащей только интеграторы, сумматоры и усилители
4.13. Перейти от передаточной функции W(p) к структурной схеме, содержащей только интеграторы, сумматоры и усилители, где
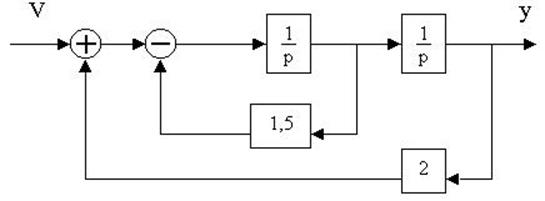
4.14. Структурная схема системы имеет вид
Определить передаточную функцию
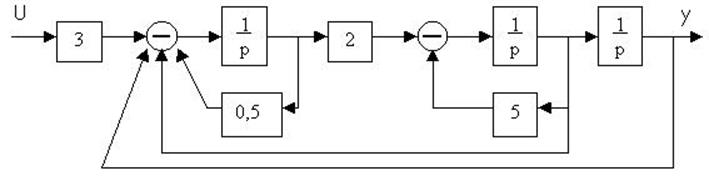
4.15. Структурная схема системы имеет вид
Определить передаточную функцию системы.
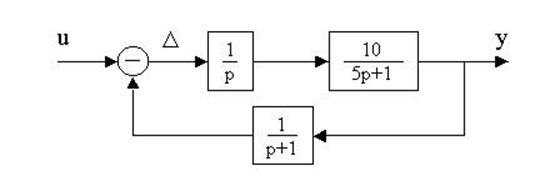
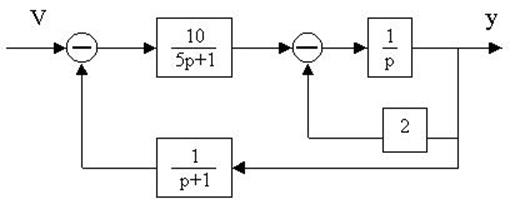
4.16. Определить W(p)=y(p)/u(p) по заданной структурной схеме и составить описание системы в пространстве состояний
4.17. По структурной схеме
определить W(p)=y(p)/u(p),составить описание в пространстве состояний.
4.18. По структурной схеме определить передаточную функцию
4.19. Для заданной структурной схемы
4.20. Структурная схема системы имеет вид
4.21.Структурная схема системы имеет вид
определить передаточную функцию W(p).
4.22.Структурная схема системы имеет вид
определить передаточную функцию W(p).
4.23.Структурная схема системы имеет вид
определить передаточную функцию W(p).
4.24.Структурная схема системы имеет вид
определить передаточную функцию W(p), записать дифференциальное уравнение относительно y, u.
4.25.Структурная схема системы имеет вид
определить передаточную функцию W(p).
4.26. Для заданной структурной
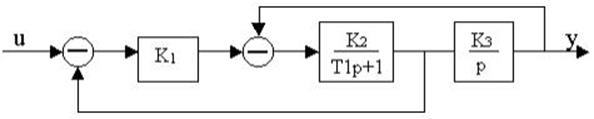
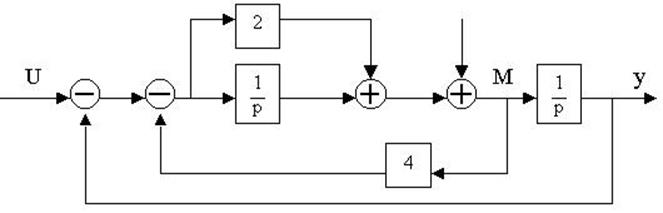
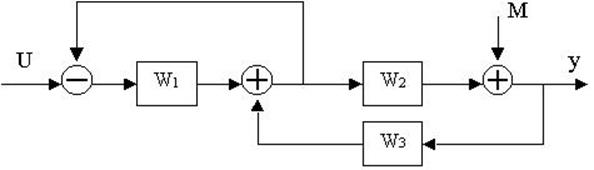
4.27. Найти передаточные функции по заданной структурной схеме W1(p)=y(p)/u(p) и W2(p)=y(p)/М(p)
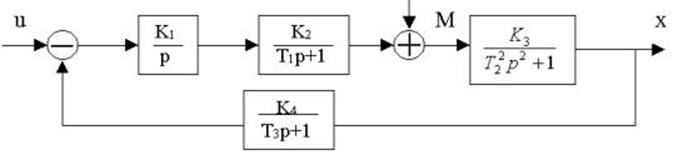
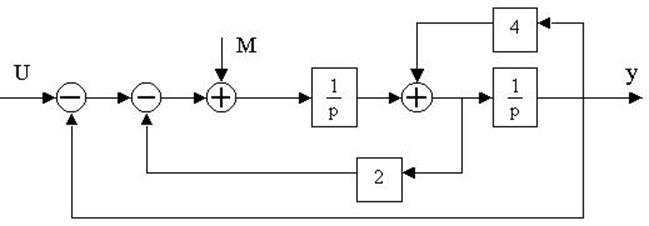
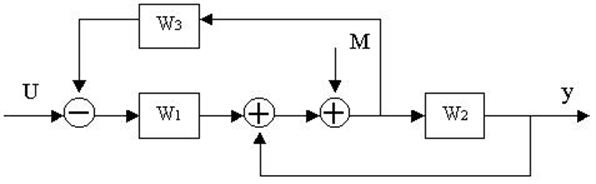
4.28. Найти передаточные функции по заданной структурной схеме W1(p)=y(p)/u(p) и W2(p)=y(p)/М(p)
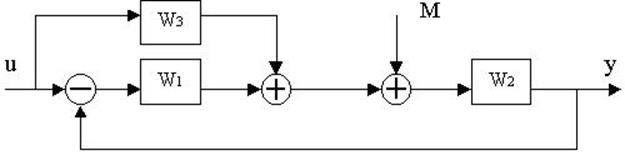
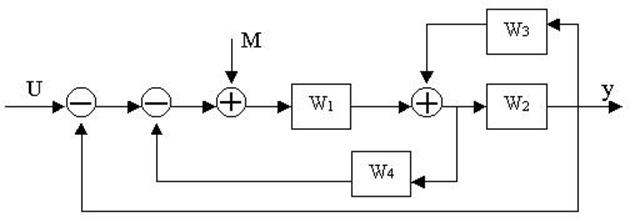
4.29. Найти передаточные функции по заданной структурной схеме W1(p)=y(p)/u(p) и W2(p)=y(p)/М(p)
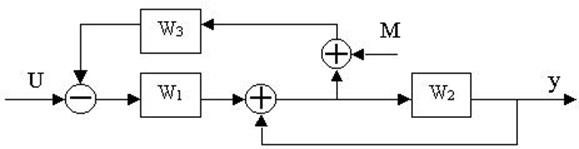
4.30. Найти передаточные функции по заданной структурной схеме W1(p)=y(p)/u(p) и W2(p)=y(p)/М(p)
4.31. Найти передаточные функции по заданной структурной схеме W1(p)=y(p)/u(p) и W2(p)=y(p)/М(p)
4.32. Найти передаточные функции по заданной структурной схеме W1(p)=y(p)/u(p) и W2(p)=y(p)/М(p)
4.33. Найти передаточные функции по заданной структурной схеме W1(p)=y(p)/u(p) и W2(p)=y(p)/М(p)
В начало
Видео:Как в MATLAB Simulink моделировать уравнения (Структурная схема САУ)Скачать
Получение структурной схемы по уравнениям
Построение структурной схемы по системе алгебраических уравнений
Пусть задана система алгебраических уравнений вида:
| 2x + 6y = 36
| 4x + 7y = 47
Выполняется преобразование схемы следующим образом. В каждом уравнении выбирается наиболее «значимая» переменная, которая остается в левой части уравнения, а всё остальное переносится в правую часть.
| 2x = 36 – 6y
| 7y = 47 – 4x
Каждое уравнение, имеющее слагаемые в правой части, на структурной схеме обозначается сумматором, на входы которого подаются слагаемые правой части с соответствующими знаками, а на выходе формируется сигнал, соответствующий левой части.
Если слагаемое правой части является свободным числом (постоянным или зависящим от времени или других переменных, не входящих в систему), то на схеме оно представляется в виде внешнего воздействия.
Если слагаемое правой части зависит от переменных системы уравнений, то эти переменные приводятся к требуемым слагаемым (например, умножаются на числа), и подключаются к сумматору.
В результате будет получена структурная схема, реализующая систему уравнений.
Построение структурной схемы по системе дифференциальных уравнений
Построение структурной схемы аналогично построению для системы алгебраических уравнений. В левой части остаются только старшие производные и вводится подстановка s = d/dt. Для получения на структурной схеме сигнала x при известном sx ставится интегратор 1/s.
Пусть задана система дифференциальных уравнений:
| x’ = x*y + 2*t
| y» = x + y — 8
В уравнениях под ‘ понимается производная первого порядка и под » — производная второго порядка. Тогда путем замены ‘ на s и, соответственно, » на s 2 получим:
| sx = x*y + 2*t
| s 2 y = x + y — 8
Далее на схему ставится 2 сумматора, на выходе которых формируются sx и s 2 y. Далее выход сумматора подключается к интегратору 1/s, в результате будет уже получены сигналы x и sy, и далее к выходу интегратора подключается ещё один интегратор, на выходе которого формируются уже сама переменная y. Далее эти переменные через коэффициенты усиления и блок умножения X подключаются к сумматорам. Кроме того, к сумматорам подключаются внешние воздействия 2*t и -8.
Структурная схема имеет следующий вид.
🔥 Видео
Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 1Скачать
Откуда появляются дифференциальные уравнения и как их решатьСкачать
Решение физических задач с помощью дифференциальных уравненийСкачать
Лекция 213. Решение дифференциального уравнения на ОУСкачать
18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать
Математика это не ИсламСкачать
Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать
